K-近邻算法学习

以下笔记来源于黑马程序员十三天入门机器学习

1 什么是K-近邻算法

• K Nearest Neighbor算法⼜叫KNN算法， 这个算法是机器学习⾥⾯⼀个⽐较经典的算法， 总体来说KNN算法是相对⽐较容易理解的算法

1.1 定义

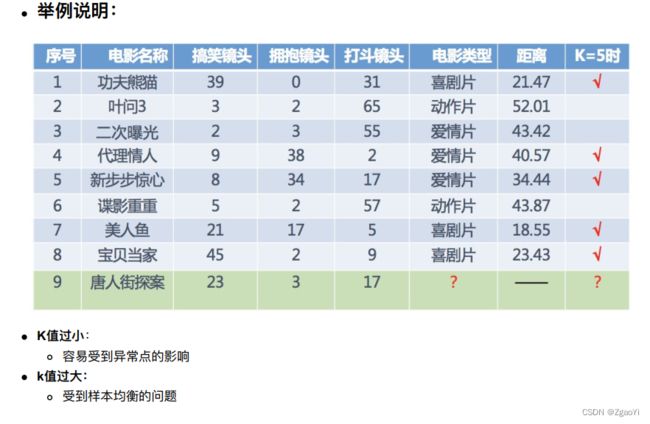
如果⼀个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的⼤多数属于某⼀个类别， 则该样本也属于这个类别。

2 k近邻算法api的初步使用

• 机器学习流程
  1.获取数据集
  2.数据基本处理
  3.特征⼯程
  4.机器学习
  5.模型评估

2.1 Scikit-learn⼯具介绍

2.1.1 安装

pip3 install scikit-learn==0.19.1

安装好之后可以通过以下命令查看是否安装成功

import sklearn

注： 安装scikit-learn需要Numpy, Scipy等库

2.1.2 K-近邻算法API

• sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
  • n_neighbors： int,可选（默认= 5） ， k_neighbors查询默认使⽤的邻居数

2.2. 案例

2.2.1 步骤分析

• 1.获取数据集
• 2.数据基本处理（该案例中省略）
• 3.特征⼯程（该案例中省略）
• 4.机器学习
• 5.模型评估（该案例中省略）

2.2.2 代码过程

• 导⼊模块

from sklearn.neighbors import KNeighborsClassifier

• 构造数据集

x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]

• 机器学习 – 模型训练

# 实例化API
estimator = KNeighborsClassifier(n_neighbors=1)
# 使⽤fit⽅法进⾏训练
estimator.fit(x, y)
estimator.predict([[1]])

3. 距离度量

3.1 距离公式的基本性质

在机器学习过程中， 对于函数 dist(., .)， 若它是⼀"距离度量" (distance measure)， 则需满⾜⼀些基本性质:

• ⾮负性： dist(X , X ) >= 0 ；
• 同⼀性： dist(x , x ) = 0。 当且仅当 X = X ；
• 对称性： dist(x , x ) = dist(x , x )；
• 直递性： dist(x , x ) <= dist(x , x ) + dist(x , x )
  • 直递性常被直接称为“三⻆不等式”。

3.2 常⻅的距离公式

3.2.1 欧式距离(Euclidean Distance)：

欧⽒距离是最容易直观理解的距离度量⽅法， 我们⼩学、 初中和⾼中接触到的两个点在空间中的距离⼀般都是指欧⽒距离。

3.2.2 曼哈顿距离(Manhattan Distance)：

在曼哈顿街区要从⼀个⼗字路⼝开⻋到另⼀个⼗字路⼝， 驾驶距离显然不是两点间的直线距离。 这个实际驾驶距离就是 “曼哈顿距离”。 曼哈顿距离也称为“城市街区距离”(City Block distance)

3.2.3 切⽐雪夫距离 (Chebyshev Distance)：

国际象棋中， 国王可以直⾏、 横⾏、 斜⾏， 所以国王⾛⼀步可以移动到相邻8个⽅格中的任意⼀个。 国王从格⼦(x1,y1) ⾛到格⼦(x2,y2)最少需要多少步？ 这个距离就叫切⽐雪夫距离。

3.2.4 闵可夫斯基距离(Minkowski Distance)：

闵⽒距离不是⼀种距离， ⽽是⼀组距离的定义， 是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

4.k值的选择

4.1 K值选择说明

4.2 KNN中K值⼤⼩选择对模型的影响

• K值过⼩：
  • 容易受到异常点的影响
  • 容易过拟合
• k值过⼤：
  • 受到样本均衡的问题
  • 容易⽋拟合

4.3 误差

• 近似误差
  • 对现有训练集的训练误差， 关注训练集，
  • 如果近似误差过⼩可能会出现过拟合的现象， 对现有的训练集能有很好的预测， 但是对未知的测试样本将会出现较⼤偏差的预测。
  • 模型本身不是最接近最佳模型。
• 估计误差
  • 可以理解为对测试集的测试误差， 关注测试集，
  • 估计误差⼩说明对未知数据的预测能⼒好，
  • 模型本身最接近最佳模型。

5 kd树

5.1 kd树简介

根据KNN每次需要预测⼀个点时， 我们都需要计算训练数据集⾥每个点到这个点的距离， 然后选出距离最近的k个点进⾏投票。 当数据集很⼤时， 这个计算成本⾮常⾼， 针对N个样本， D个特征的数据集， 其算法复杂度为O（DN ） 。
kd树： 为了避免每次都重新计算⼀遍距离， 算法会把距离信息保存在⼀棵树⾥， 这样在计算之前从树⾥查询距离信息，
尽量避免重新计算。 其基本原理是， 如果A和B距离很远， B和C距离很近， 那么A和C的距离也很远。 有了这个信息，就可以在合适的时候跳过距离远的点。

5.2 原理

5.3 构造⽅法

（1） 构造根结点， 使根结点对应于K维空间中包含所有实例点的超矩形区域；
（2） 通过递归的⽅法， 不断地对k维空间进⾏切分， ⽣成⼦结点。 在超矩形区域上选择⼀个坐标轴和在此坐标轴上的⼀
个切分点， 确定⼀个超平⾯， 这个超平⾯通过选定的切分点并垂直于选定的坐标轴， 将当前超矩形区域切分为左右两个
⼦区域（⼦结点） ； 这时， 实例被分到两个⼦区域。
（3） 上述过程直到⼦区域内没有实例时终⽌（终⽌时的结点为叶结点） 。 在此过程中， 将实例保存在相应的结点上。
（4） 通常， 循环的选择坐标轴对空间切分， 选择训练实例点在坐标轴上的中位数为切分点， 这样得到的kd树是平衡的
（平衡⼆叉树： 它是⼀棵空树， 或其左⼦树和右⼦树的深度之差的绝对值不超过1， 且它的左⼦树和右⼦树都是平衡⼆
叉树） 。
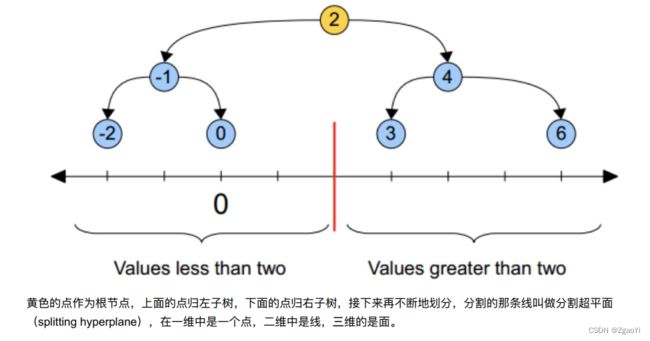
KD树中每个节点是⼀个向量， 和⼆叉树按照数的⼤⼩划分不同的是， KD树每层需要选定向量中的某⼀维， 然后根据这
⼀维按左⼩右⼤的⽅式划分数据。 在构建KD树时， 关键需要解决2个问题：
（1） 选择向量的哪⼀维进⾏划分；
（2） 如何划分数据；
第⼀个问题简单的解决⽅法可以是随机选择某⼀维或按顺序选择， 但是更好的⽅法应该是在数据⽐较分散的那⼀维进⾏
划分（分散的程度可以根据⽅差来衡量） 。
第⼆个问题中， 好的划分⽅法可以使构建的树⽐较平衡， 可以每次选择中位数来进⾏划分。

5.4 案例分析

5.4.1 树的建立

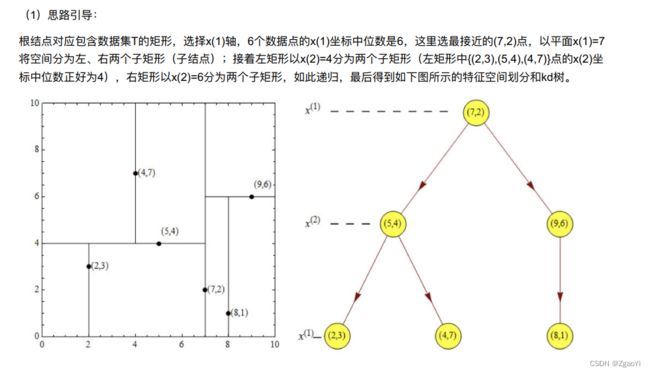
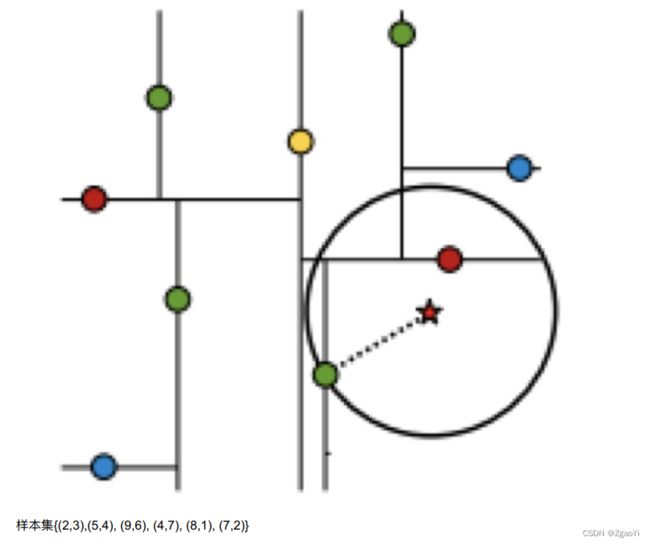
给定⼀个⼆维空间数据集： T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}， 构造⼀个平衡kd树

5.4.2 最近领域的搜索

假设标记为星星的点是 test point， 绿⾊的点是找到的近似点， 在回溯过程中， 需要⽤到⼀个队列， 存储需要回溯的点， 在判断其他⼦节点空间中是否有可能有距离查询点更近的数据点时， 做法是以查询点为圆⼼， 以当前的最近距离为半径画圆， 这个圆称为候选超球（candidate hypersphere） ， 如果圆与回溯点的轴相交， 则需要将轴另⼀边的节点都放
到回溯队列⾥⾯来。

5.4.3 查找点（2.1，3.1）

在(7,2)点测试到达(5,4)， 在(5,4)点测试到达(2,3)， 然后search_path中的结点为<(7,2),(5,4), (2,3)>， 从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；
然后回溯⾄(5,4)， 以(2.1,3.1)为圆⼼， 以dist=0.141为半径画⼀个圆， 并不和超平⾯y=4相交， 如上图， 所以不必跳到结点(5,4)的右⼦空间去搜索， 因为右⼦空间中不可能有更近样本点了。
于是再回溯⾄(7,2)， 同理， 以(2.1,3.1)为圆⼼， 以dist=0.141为半径画⼀个圆并不和超平⾯x=7相交， 所以也不⽤跳到结点(7,2)的右⼦空间去搜索。
⾄此， search_path为空， 结束整个搜索， 返回nearest(2,3)作为(2.1,3.1)的最近邻点， 最近距离为0.141。

5.4.4 查找点(2,4.5)

在(7,2)处测试到达(5,4)， 在(5,4)处测试到达(4,7)【优先选择在本域搜索】 ， 然后search_path中的结点为<(7,2),(5,4),(4,7)>， 从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；然后回溯⾄(5,4)， 以(2,4.5)为圆⼼， 以dist=3.202为半径画⼀个圆与超平⾯y=4相交， 所以需要跳到(5,4)的左⼦空间去搜索。 所以要将(2,3)加⼊到search_path中， 现在search_path中的结点为<(7,2),(2, 3)>； 另外， (5,4)与(2,4.5)的距离为3.04 < dist = 3.202， 所以将(5,4)赋给nearest， 并且dist=3.04。
回溯⾄(2,3)， (2,3)是叶⼦节点， 直接平判断(2,3)是否离(2,4.5)更近， 计算得到距离为1.5， 所以nearest更新为(2,3)，dist更新为(1.5)
回溯⾄(7,2)， 同理， 以(2,4.5)为圆⼼， 以dist=1.5为半径画⼀个圆并不和超平⾯x=7相交, 所以不⽤跳到结点(7,2)的右⼦空间去搜索。
⾄此， search_path为空， 结束整个搜索， 返回nearest(2,3)作为(2,4.5)的最近邻点， 最近距离为1.5。

6. 案例： 鸢尾花种类预测–数据集介绍

6.1 案例： 鸢尾花种类预测

6.2 scikit-learn中数据集介绍

6.2.1 scikit-learn数据集API介绍

• sklearn.datasets
  • 加载获取流⾏数据集
  • datasets.load_*()
    • 获取⼩规模数据集， 数据包含在datasets⾥
  • datasets.fetch_*(data_home=None)
    • 获取⼤规模数据集， 需要从⽹络上下载， 函数的第⼀个参数是data_home， 表示数据集下载的⽬录,默认是 ~/scikit_learn_data/

6.2.1.1 sklearn⼩数据集

6.2.1.2 sklearn⼤数据集

• sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
  • subset： ‘train’或者’test’， ‘all’， 可选， 选择要加载的数据集。
  • 训练集的“训练”， 测试集的“测试”， 两者的“全部”

6.2.2 sklearn数据集返回值介绍

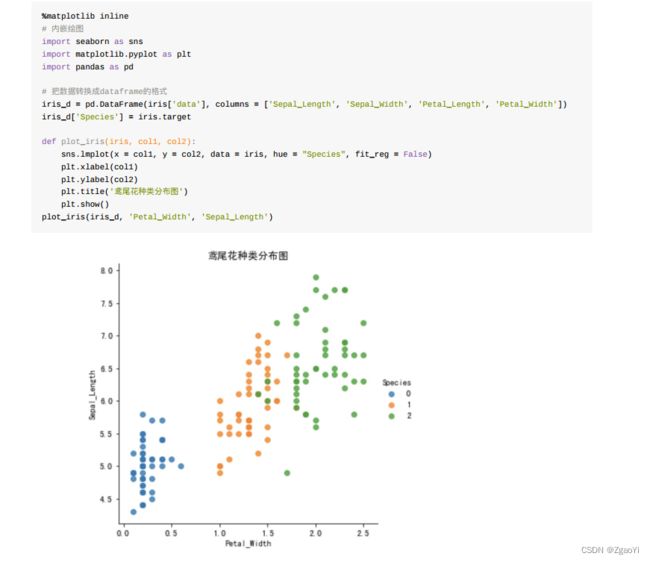
6.2.3 查看数据分布

通过创建⼀些图， 以查看不同类别是如何通过特征来区分的。 在理想情况下， 标签类将由⼀个或多个特征对完美分隔。 在现实世界中， 这种理想情况很少会发⽣。

6.2.4 数据集的划分

7 特征⼯程-特征预处理

7.1 什么是特征预处理

7.1.1 定义

通过⼀些转换函数将特征数据转换成更加适合算法模型的特征数据过程

• 为什么我们要进⾏归⼀化/标准化？
  • 特征的单位或者⼤⼩相差较⼤， 或者某特征的⽅差相⽐其他的特征要⼤出⼏个数量级， 容易影响（⽀配） ⽬标结果， 使得⼀些算法⽆法学习到其它的特征

7.2 特征预处理API

sklearn.preprocessing

7.3 归一化

7.3.1 定义

通过原始数据进行变换把数据映射到（默认为[0,1]）之间

7.3.2 公式

例子：

7.3.3 API

• sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
  • MinMaxScalar.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
  • 返回值： 转换后的形状相同的array

7.3.4 数据计算

我们对以下数据进⾏运算， 在dating.txt中。 保存的就是之前的约会对象数据

milage,Liters,Consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1
38344,1.669788,0.134296,1

• 分析
  1、 实例化MinMaxScalar
  2、 通过fit_transform转换

import pandas as pd
from sklearn.preprocessing import MinMaxScaler
def minmax_demo():
"""
归⼀化演示
:return: None
"""
data = pd.read_csv("./data/dating.txt")
print(data)
# 1、 实例化⼀个转换器类
transfer = MinMaxScaler(feature_range=(2, 3))
# 2、 调⽤fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("最⼩值最⼤值归⼀化处理的结果： \n", data)
return None

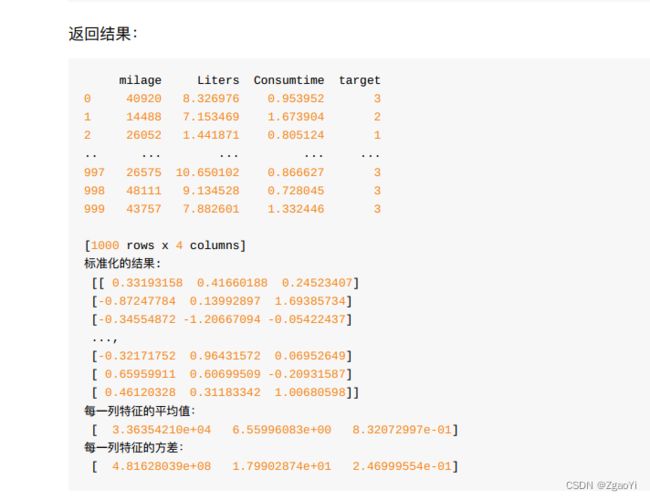
返回结果：

7.3.5 归一化总结

注意最⼤值最⼩值是变化的， 另外， 最⼤值与最⼩值⾮常容易受异常点影响， 所以这种⽅法鲁棒性较差， 只适合传统精确⼩数据场景。

7.4 标准化

7.4.1 定义

通过对原始数据进行变换把数据变换到均值为0，标准差为1的范围内

7.4.2 公式

• 对于归⼀化来说： 如果出现异常点， 影响了最⼤值和最⼩值， 那么结果显然会发⽣改变
• 对于标准化来说： 如果出现异常点， 由于具有⼀定数据量， 少量的异常点对于平均值的影响并不⼤， 从⽽⽅差改变较⼩。

7.4.3 API

• sklearn.preprocessing.StandardScaler( )
  • 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
  • StandardScaler.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
  • 返回值： 转换后的形状相同的array

7.4.4 数据计算

同样对上⾯的数据进⾏处理

• 分析
  1、 实例化StandardScaler
  2、 通过fit_transform转换

import pandas as pd
from sklearn.preprocessing import StandardScaler
def stand_demo():
"""
标准化演示
:return: None
"""
data = pd.read_csv("dating.txt")
print(data)
# 1、 实例化⼀个转换器类
transfer = StandardScaler()
# 2、 调⽤fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("标准化的结果:\n", data)
print("每⼀列特征的平均值： \n", transfer.mean_)
print("每⼀列特征的⽅差： \n", transfer.var_)
return None

7.4.5 标准化总结

在已有样本⾜够多的情况下⽐较稳定， 适合现代嘈杂⼤数据场景。

总结：

8 案例： 鸢尾花种类预测—流程实现

8.1 再识K-近邻算法API

• sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
  • n_neighbors：
    • int,可选（默认= 5） ， k_neighbors查询默认使⽤的邻居数
  • algorithm： {‘auto’， ‘ball_tree’， ‘kd_tree’， ‘brute’}
    • 快速k近邻搜索算法， 默认参数为auto， 可以理解为算法⾃ ⼰决定合适的搜索算法。 除此之外， ⽤户也可以⾃ ⼰指定搜索算法ball_tree、 kd_tree、 brute⽅法进⾏搜索，
      • brute是蛮⼒搜索， 也就是线性扫描， 当训练集很⼤时， 计算⾮常耗时。
      • kd_tree， 构造kd树存储数据以便对其进⾏快速检索的树形数据结构， kd树也就是数据结构中的⼆叉树。 以中值切分构造的树， 每个结点是⼀个超矩形， 在维数⼩于20时效率⾼。
      • ball tree是为了克服kd树⾼维失效⽽发明的， 其构造过程是以质⼼C和半径r分割样本空间， 每个节点是⼀个超球体。

8.2 鸢尾花种类预测

8.2.1 数据集介绍

Iris数据集是常⽤的分类实验数据集， 由Fisher, 1936收集整理。 Iris也称鸢尾花卉数据集， 是⼀类多重变量分析的数据集。 关于数据集的具体介绍：

8.2.2 步骤分析

1.获取数据集
2.数据基本处理
3.特征⼯程
4.机器学习(模型训练)
5.模型评估

8.2.3 代码过程

• 导入模块

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

• 先从sklearn当中获取数据集， 然后进⾏数据集的分割

# 1.获取数据集
iris = load_iris()
# 2.数据基本处理
# x_train,x_test,y_train,y_test为训练集特征值、 测试集特征值、 训练集⽬标值、 测试集⽬标值
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)

• 进⾏数据标准化
  • 特征值的标准化

# 3、 特征⼯程： 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

• 模型进⾏训练预测

# 4、 机器学习(模型训练)
estimator = KNeighborsClassifier(n_neighbors=9)
estimator.fit(x_train, y_train)
# 5、 模型评估
# ⽅法1： ⽐对真实值和预测值
y_predict = estimator.predict(x_test)
print("预测结果为:\n", y_predict)
print("⽐对真实值和预测值： \n", y_predict == y_test)
# ⽅法2： 直接计算准确率
score = estimator.score(x_test, y_test)
print("准确率为： \n", score)

9. KNN算法总结

9.1 k近邻算法优缺点汇总

• 优点：

  • 简单有效
  • 重新训练的代价低
  • 适合类域交叉样本
    • KNN⽅法主要靠周围有限的邻近的样本,⽽不是靠判别类域的⽅法来确定所属类别的， 因此对于类域的交叉或重叠较多的待分样本集来说， KNN⽅法较其他⽅法更为适合。
  • 适合⼤样本⾃动分类
    • 该算法⽐较适⽤于样本容量⽐较⼤的类域的⾃动分类， ⽽那些样本容量较⼩的类域采⽤这种算法⽐较容易产⽣误分。

• 缺点：

  • 惰性学习
    • KNN算法是懒散学习⽅法（lazy learning,基本上不学习） ， ⼀些积极学习的算法要快很多
  • 类别评分不是规格化
    • 不像⼀些通过概率评分的分类
  • 输出可解释性不强
    • 例如决策树的输出可解释性就较强
  • 对不均衡的样本不擅⻓
    • 当样本不平衡时， 如⼀个类的样本容量很⼤， ⽽其他类样本容量很⼩时， 有可能导致当输⼊⼀个新样本时， 该样本的K个邻居中⼤容量类的样本占多数。 该算法只计算“最近的”邻居样本， 某⼀类的样本数量很⼤， 那么或者这类样本并不接近⽬ 标样本， 或者这类样本很靠近⽬ 标样本。 ⽆论怎样， 数量并不能影响运⾏结果。 可以采⽤权值的⽅法（和该样本距离⼩的邻居权值⼤） 来改进。
  • 计算量较⼤
    • ⽬前常⽤的解决⽅法是事先对已知样本点进⾏剪辑， 事先去除对分类作⽤不⼤的样本。

10 交叉验证， ⽹格搜索

10.1 什么是交叉验证(cross validation)

交叉验证： 将拿到的训练数据， 分为训练和验证集。 以下图为例： 将数据分成4份， 其中⼀份作为验证集。 然后经过4次(组)的测试， 每次都更换不同的验证集。 即得到4组模型的结果， 取平均值作为最终结果。 ⼜称4折交叉验证。

10.1.1 分析

我们之前知道数据分为训练集和测试集， 但是为了让从训练得到模型结果更加准确。 做以下处理

• 训练集： 训练集+验证集
• 测试集： 测试集
  

10.1.2 为什么需要交叉验证

交叉验证⽬ 的： 为了让被评估的模型更加准确可信

10.2 什么是网格搜索（Grid Search）

通常情况下， 有很多参数是需要⼿动指定的（如k-近邻算法中的K值） ， 这种叫超参数。 但是⼿动过程繁杂， 所以需要对模型预设⼏种超参数组合。 每组超参数都采⽤交叉验证来进⾏评估。 最后选出最优参数组合建⽴模型

10.3 交叉验证， ⽹格搜索（模型选择与调优） API：

• sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
  • 对估计器的指定参数值进⾏详尽搜索
  • estimator： 估计器对象
  • param_grid： 估计器参数(dict){“n_neighbors”:[1,3,5]}
  • cv： 指定⼏折交叉验证
  • fit： 输⼊训练数据
  • score： 准确率
  • 结果分析：
    • bestscore__:在交叉验证中验证的最好结果
    • bestestimator： 最好的参数模型
    • cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

10.4 鸢尾花案例增加K值调优

• 使⽤GridSearchCV构建估计器

# 1、 获取数据集
iris = load_iris()
# 2、 数据基本处理 -- 划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3、 特征⼯程： 标准化
# 实例化⼀个转换器类
transfer = StandardScaler()
# 调⽤fit_transform
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、 KNN预估器流程
# 4.1 实例化预估器类
estimator = KNeighborsClassifier()
# 4.2 模型选择与调优——⽹格搜索和交叉验证
# 准备要调的超参数
param_dict = {"n_neighbors": [1, 3, 5]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 4.3 fit数据进⾏训练
estimator.fit(x_train, y_train)
# 5、 评估模型效果
# ⽅法a： ⽐对预测结果和真实值
y_predict = estimator.predict(x_test)
print("⽐对预测结果和真实值： \n", y_predict == y_test)
# ⽅法b： 直接计算准确率
score = estimator.score(x_test, y_test)
print("直接计算准确率： \n", score)

• 然后进⾏评估查看最终选择的结果和交叉验证的结果

print("在交叉验证中验证的最好结果： \n", estimator.best_score_)
print("最好的参数模型： \n", estimator.best_estimator_)
print("每次交叉验证后的准确率结果： \n", estimator.cv_results_)

最终结果：

总结：