机器学习之算法优化（一）

---

前言

Geatpy是一个高性能实用型进化算法工具箱，可用于求解单目标优化、多目标优化、复杂约束优化、组合优化、混合编码进化优化等。内部封装了多种算法，包括遗传算法，差分进化算法，群粒子算法，模拟退火算法等。

Geatpy文档：http://geatpy.com/index.php/%e6%80%bb%e8%a7%88/

安装：

pip install geatpy

Geatpy架构说明

Geatpy2整体上看由工具箱内核函数（内核层）和面向对象进化算法框架（框架层）两部分组成。其中面向对象进化算法框架主要有四个大类：Problem问题类、Algorithm算法模板类、Population种群类和PsyPopulation多染色体种群类。UML图如下所示：

• Problem
  Problem类定义了与问题相关的一些信息，如问题名称name、优化目标的维数M、决策变量的个数Dim、决策变量的范围ranges、决策变量的边界borders等。maxormins是一个记录着各个目标函数是最小化抑或是最大化的Numpy array行向量，其中元素为1表示对应的目标是最小化目标；为-1表示对应的是最大化目标。例如M=3，maxormins=array([1,-1,1])，此时表示有三个优化目标，其中第一、第三个是最小化目标，第二个是最大化目标。varTypes是一个记录着决策变量类型的行向量，其中的元素为0表示对应的决策变量是连续型变量；为1表示对应的是离散型变量。待求解的目标函数定义在aimFunc()的函数中。calReferObjV()函数则用于计算或读取目标函数参考值（一般用理论上的目标函数的最优值作为参考值）；getReferObjV()是Problem父类中已经实现了的一个函数，它先尝试读取特定文件夹中的目标函数值参考数据，如果读取不到，则调用calReferObjV()进行计算。
• Algorithm
  Algorithm 类是进化算法的核心类。它既存储着跟进化算法相关的一些参数，同时也在其继承类中实现具体的进化算法。
• Population
  Population 类是一个表示种群的类。一个种群包含很多个个体，而每个个体都有一条染色体(若要用多染色体，则使用多个种群、并把每个种群对应个体关联起来即可)。除了染色体外，每个个体都有一个译码矩阵Field(或俗称区域描述器) 来标识染色体应该如何解码得到表现型，同时也有其对应的目标函数值以及适应度。种群类就是一个把所有个体的这些数据统一存储起来的一个类。比如里面的Chrom 是一个存储种群所有个体染色体的矩阵，它的每一行对应一个个体的染色体；ObjV 是一个目标函数值矩阵，每一行对应一个个体的所有目标函数值，每一列对应一个目标。
• PsyPopulation
  PsyPopulation类是继承了Population的支持多染色体混合编码的种群类。一个种群包含很多个个体，而每个个体都有多条染色体。用Chroms列表存储所有的染色体矩阵(Chrom)；Encodings列表存储各染色体对应的编码方式(Encoding)；Fields列表存储各染色体对应的译码矩阵(Field)。EncoIdxs是一个list，其元素表示每条染色体对应编码哪一个变量。比如EncoIdxs = [[0], [1,2,3,4]]，表示一共有5个变量，其中第一个变量编码成第一条子染色体；后4个变量编码成第二条子染色体。

这些算法模板通过调用Geatpy 工具箱提供的进化算法库函数实现对种群的进化操作，同时记录进化过程中的相关信息，其基本层次结构如下图：

其中“算子类”是Geatpy2.2.2版本之后增加的特性，通过实例化算子类来调用低级操作函数，可以利用面向对象编程的优势使得对传入低级操作函数的一些参数的修改变得更加方便。目前内置的“算子类”有“重组算子类”和“变异算子类”。用户可以绕开对底层的低级操作函数的修改而直接通过新增“算子类”来实现新的算子例如自适应的重组、变异算子等。

Geatpy工具中求解函数optimize说明

optimize(algorithm, seed=None, prophet=None, 
         verbose=None, drawing=None, outputMsg=True,
         drawLog=True, saveFlag=True, dirName=None, 
         **kwargs)

参数说明：

    algorithm : 算法类的引用。

    seed      : int  - 随机数种子。

    prophet   :  / Numpy ndarray - 先验知识。可以是种群对象，
                      也可以是一组或多组决策变量组成的矩阵（矩阵的每一行对应一组决策变量）。默认为None。

    verbose   : bool - 控制是否在输入输出流中打印输出日志信息。
                       该参数将被传递给algorithm.verbose。
                       如果algorithm已设置了该参数的值，则调用optimize函数时，可以不传入该参数。
                       默认为None。

    drawing   : int  - 算法类控制绘图方式的参数，
                       0表示不绘图；
                       1表示绘制最终结果图；
                       2表示实时绘制目标空间动态图；
                       3表示实时绘制决策空间动态图。
                       该参数将被传递给algorithm.drawing。
                       如果algorithm已设置了该参数的值，则调用optimize函数时，可以不传入该参数。
                       默认为None。

    outputMsg : bool - 控制是否输出结果以及相关指标信息。默认为True。

    drawLog   : bool - 用于控制是否根据日志绘制迭代变化图像。默认为True。

    saveFlag  : bool - 控制是否保存结果。默认为True。

    dirName   : str  - 文件保存的路径。当缺省或为None时，默认保存在当前工作目录的'result of job xxxx-xx-xx xxh-xxm-xxs'文件夹下。
                       默认为None。

输出参数:
    result    : dict - 一个保存着结果的字典。内容为：
                       {'success': True or False,  # 表示算法是否成功求解。
                        'stopMsg': xxx,  # 存储着算法停止原因的字符串。
                        'optPop': xxx,  # 存储着算法求解结果的种群对象。如果无可行解，则optPop.sizes=0。optPop.Phen为决策变量矩阵，optPop.ObjV为目标函数值矩阵。
                        'lastPop': xxx,  # 算法进化结束后的最后一代种群对象。
                        'Vars': xxx,  # 等于optPop.Phen，此处即最优解。若无可行解，则Vars=None。
                        'ObjV': xxx,  # 等于optPop.ObjV，此处即最优解对应的目标函数值。若无可行解，ObjV=None。
                        'CV': xxx,  # 等于optPop.CV，此处即最优解对应的违反约束程度矩阵。若无可行解，CV=None。
                        'startTime': xxx,  # 程序执行开始时间。
                        'endTime': xxx,  # 程序执行结束时间。
                        'executeTime': xxx,  # 算法所用时间。
                        'nfev': xxx,  # 算法评价次数
                        'gd': xxx,  # (多目标优化且给定了理论最优解时才有) GD指标值。
                        'igd': xxx,  # (多目标优化且给定了理论最优解时才有) IGD指标值。
                        'hv': xxx,  # (多目标优化才有) HV指标值。
                        'spacing': xxx # (多目标优化才有) Spacing指标值。
                        }

一、遗传算法精英保留策略

1.单目标遗传算法精英保留策略概念

遗传算法(Genetic Algorithm)中的基因，并不一定真实地反映了待求解问题的本质，因此各个基因之间未必就相互独立，如果只是简单地进行杂交，很可能把较好的组合给破坏了，这样就没有达到累积较好基因的目的，反而把原本很好的基因给破坏了。精英保留策略可以避免最优个体不会因为杂交操作而被破坏。
精英保留策略：是针对遗传算法提出来的。对遗传算法来说，能否收敛到全局最优解是其首要问题。De Jong提出该策略的思想是，把群体在进化过程中迄今出现的最好个体(称为精英个体elitist)不进行配对交叉而直接复制到下一代中。 这种选择操作又称为复制(copy)。

标准遗传算法不能全局收敛的主要原因：

• (1) 采用比例选择法，由于存在统计误差，依据产生的随机数进行选择，有可能会出现不正确地反映个体适应度的选择，可能导致适应度高的个体也被淘汰掉；

• (2) 交叉、变异算子可能会破坏掉个体中所隐含的高阶(high-order)、长距(length)、高平均适应度模式(schema)，可能导致当前群体中的最优个体在下一代群体中发生丢失，而且这种最优个体丢失现象会周而复始的出现在进化过程中。

De Jong对精英保留策略方法作了如下定义：

设到第t代时，群体中 a(t)为最优个体。又设A(t+1)为新一代群体，若A(t+1)中不存在比a(t)优的个体，则把a(t)加入到A(t+1)中作为A(t+1)的第n+1个个体，这里n为群体的大小。

为了保持群体的规模不变，如果精英个体被加入到新一代群体中，则将新一代群体中适应度值最差的个体就淘汰掉。

• 一种做法，将精英个体放入到种群中，即种群规模为 N+1。 一种做法，保持种群规模，即将精英个体替换掉种群做的最差个体。

精英个体是种群进化到当前为止遗传算法搜索到的适应度值最高的个体，它具有最好的基因结构和优良特性。采用精英保留的优点是，遗传算法在进化过程中，迄今出现的最优个体不会被选择、交叉和变异操作所丢失和破坏。精英保留策略对改进标准遗传算法的全局收敛能力产生了重大作用，Rudolph已经从理论上证明了 具有精英保留的标准遗传算法是全局收敛的。

2.SEGA算法解决单目标遗传问题实例

问题1：

量的范围。

增强精英保留策略的遗传算法SEGA步骤：

• 第一步：先定义目标函数
• 第二步：创建问题
• 第三步：构建算法
• 第四步：调用optimize()函数来求解

用Geatpy工具中SEGA算法解决问题1：

import geatpy as ea
import numpy as np

# 构建问题
r = 1  # 目标函数需要用到的额外数据
@ea.Problem.single
# 让目标函数的传入参数是一个Numpy ndarray类型的一维数组，它的实际含义是种群的某个个体对应的决策变量。
def evalVars(Vars):  # 定义目标函数（含约束）
    f = np.sum((Vars - r) ** 2)  # 计算目标函数值（函数表达式）
    x1 = Vars[0]
    x2 = Vars[1]
    # 先把约束条件转成线性约束条件（等式右边是0）
    CV = np.array([(x1 - 0.5)**2 - 0.25,
                    (x2 - 1)**2 - 1])  # 不等式约束（计算违反约束程度）
    return f, CV                       # 返回目标函数值和违反约束程度

problem = ea.Problem(name='增强精英保留策略的遗传算法',
                        M=1,  # 目标维数
                        maxormins=[1],  # 目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标
                        Dim=5,  # 决策变量维数（个数为5）
                        varTypes=[0, 0, 1, 1, 1], # 决策变量的类型列表，0：实数；1：整数。0表示对应的决策变量是连续型变量；为1表示对应的是离散型变量。
                        lb=[-1, 1, 2, 1, 0],  # 决策变量下界
                        ub=[1, 4, 5, 2, 1],  # 决策变量上界
                        evalVars=evalVars)
# 构建算法
algorithm = ea.soea_SEGA_templet(problem,
                                 # Encoding='RI实整数编，NIND=20设定了种群有20个个体。
                                    ea.Population(Encoding='RI', NIND=20),
                                    MAXGEN=50,  # 最大进化代数。
                                    logTras=1,  # 表示每隔多少代记录一次日志信息，0表示不记录。
                                    trappedValue=1e-6,  # 单目标优化陷入停滞的判断阈值。
                                    maxTrappedCount=10)  # 进化停滞计数器最大上限值。
# 求解
res = ea.optimize(algorithm, seed=1, verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True, dirName='result')

输出为：

==================================================================================
gen|  eval  |    f_opt    |    f_max    |    f_avg    |    f_min    |    f_std    
----------------------------------------------------------------------------------
 0 |   20   | 9.18566E+00 | 9.18566E+00 | 9.18566E+00 | 9.18566E+00 | 0.00000E+00 
 1 |   40   | 5.78235E+00 | 9.18566E+00 | 8.33483E+00 | 5.78235E+00 | 1.47368E+00 
 2 |   60   | 5.78235E+00 | 1.01857E+01 | 8.44530E+00 | 5.78235E+00 | 1.56014E+00 
 3 |   80   | 5.18566E+00 | 9.18566E+00 | 7.10178E+00 | 5.18566E+00 | 1.70646E+00 
 4 |  100   | 2.18566E+00 | 5.78235E+00 | 5.31974E+00 | 2.18566E+00 | 1.00074E+00 
 5 |  120   | 2.18566E+00 | 5.71252E+00 | 4.47875E+00 | 2.18566E+00 | 1.38039E+00 
 6 |  140   | 2.18566E+00 | 5.18566E+00 | 2.88560E+00 | 2.18566E+00 | 1.09847E+00 
 7 |  160   | 2.02037E+00 | 2.18566E+00 | 2.15260E+00 | 2.02037E+00 | 6.61145E-02 
 8 |  180   | 2.00000E+00 | 2.18565E+00 | 2.02762E+00 | 2.00000E+00 | 3.65244E-02 
 9 |  200   | 2.00000E+00 | 2.02037E+00 | 2.01625E+00 | 2.00000E+00 | 8.12936E-03 
 10|  220   | 2.00000E+00 | 2.02037E+00 | 2.00908E+00 | 2.00000E+00 | 9.96122E-03 
 11|  240   | 1.00000E+00 | 2.00000E+00 | 1.95000E+00 | 1.00000E+00 | 2.17945E-01 
 12|  260   | 1.00000E+00 | 2.00000E+00 | 1.80000E+00 | 1.00000E+00 | 4.00000E-01 
 13|  280   | 1.00000E+00 | 2.00000E+00 | 1.45000E+00 | 1.00000E+00 | 4.97494E-01 
 14|  300   | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00 
 15|  320   | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00 
 16|  340   | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00
 
Execution time: 0.013827323913574219 s
Evaluation number: 340
The best objective value is: 1.0
The best variables are: 
1.0	1.0	2.0	1.0	1.0

• 上述代码中 Encoding=‘RI’ 表示改种群的染色体是’RI’编码，即“实数整数混合编码”，简称“实整数编码”。类似的还有’P’编码（排列编码，可以让对应的变量互不相同）、'BG’编码（二进制/格雷码编码）。

3.SEGA算法中对于定义目标函数有几种方法

1.方法一

    def aimFunc(pop):  # 定义目标函数（含约束）
        Vars = pop.Phen
        pop.ObjV = np.sum((Vars - r)**2, 1,
                          keepdims=True)  # 计算目标函数值，赋值给种群对象的ObjV属性
        x1 = Vars[:, [0]]  # 把Vars的第0列取出来
        x2 = Vars[:, [1]]  # 把Vars的第1列取出来
        pop.CV = np.hstack([(x1 - 0.5)**2 - 0.25,
                            (x2 - 1)**2 - 1])  # 计算违反约束程度值，赋值给种群对象的CV属性

说明：

这里的目标函数定义成aimFunc，而不是evalVars。
aimFunc(pop)传入的是一个种群对象pop。
pop.Phen是种群的表现型矩阵，等价于决策变量矩阵。它是Numpy ndarray的二维数组，每一行表示一组决策变量值。
pop.ObjV是种群的目标函数值矩阵。它是Numpy ndarray的二维数组，每一行表示一组目标函数值。
pop.CV是种群的违反约束程度矩阵。它是Numpy ndarray的二维数组，每一行表示一组违反约束程度值。

2.方法二

    def evalVars(Vars):  # 定义目标函数（含约束）
        ObjV = np.sum((Vars - r)**2, 1, keepdims=True)  # 计算目标函数值
        x1 = Vars[:, [0]]  # 把Vars的第0列取出来
        x2 = Vars[:, [1]]  # 把Vars的第1列取出来
        CV = np.hstack([(x1 - 0.5)**2 - 0.25, (x2 - 1)**2 - 1])  # 计算违反约束程度
        return ObjV, CV  # 返回目标函数值矩阵和违反约束程度矩阵

说明：

这里的目标函数定义成evalVars，而不是aimFunc。
区别：
aimFunc(pop)传入的是一个种群对象。
而evalVars(Vars)传入的是一个Numpy ndarray二维数组。其每一行的所有元素表示一组决策变量。
函数evalVars可以有一个或两个返回值。第一个返回值表示目标函数值矩阵；第二个返回值表示违反约束程度矩阵。
如果没有约束，则只需返回一个返回值即可。因此用法为：
ObjV = evalVars(Vars) 或 ObjV, CV = evalVars(Vars)

3.方法三

def evalVars(Vars):  # 定义目标函数（含约束）
        f = []  # 存储目标函数值
        CV = []  # 存储违反约束程度
        for i in range(Vars.shape[0]):  # 遍历每一组决策变量，计算对应的目标函数值
            f.append(np.sum((Vars[i, :] - r)**2))  # 用Vars[i, :] 取出每一组决策变量
            x1 = Vars[i, 0]
            x2 = Vars[i, 1]
            CV.append(np.array([(x1 - 0.5)**2 - 0.25, (x2 - 1)**2 - 1]))
        return np.vstack(f), np.vstack(CV)  # 返回目标函数值矩阵和违反约束程度矩阵

说明：

与上面不同的是本案例采用循环计算每个个体的目标函数值和违反约束程度值。

4.方法四

    @ea.Problem.single
    def evalVars(Vars):  # 定义目标函数（含约束）
        f = np.sum((Vars - r)**2)  # 计算目标函数值
        x1 = Vars[0]
        x2 = Vars[1]
        CV = np.array([(x1 - 0.5)**2 - 0.25, (x2 - 1)**2 - 1])  # 计算违反约束程度
        return f, CV

说明：

本案例通过装饰器single标记目标函数evalVars，使得目标函数只传入一组决策变量。
此时目标函数只需计算这组变量对应的目标函数值以及违反约束程度值。
用法：
ObjV = evalVars(Vars) – 若无约束 或 ObjV, CV = evalVars(Vars) – 若有约束
注意：
加了装饰器single后，evalVars的传入参数Vars不再是Numpy ndarray二维数组，而是Numpy ndarray一维数组。
在设置返回值时：
返回值ObjV可以赋值为一个Numpy ndarray一维数组，也可以是一个标量（当只有一个优化目标时）。
返回值CV可以赋值为一个Numpy ndarray一维数组，也可以是一个标量（当只有一个优化目标时）。
值得注意的是：
通过调用evalVars(Vars)得到的返回值会被single装饰器修正为Numpy ndarray二维数组。
即ObjV = evalVars(Vars)得到的ObjV或：ObjV, CV = evalVars(Vars)得到的ObjV和CV，均为Numpy ndarray二维数组。

二、NSGA2算法双目标优化问题

NSGA2多目标遗传算法介绍：https://blog.csdn.net/q15615725386/article/details/119521206

1.NSGA2算法概念

NSGA算法是以遗传算法为基础并基于Pareto最优概念得到的。NSGA算法与标准遗传算法的主要区别是其在进行选择操作之前对个体进行了快速非支配排序，增大了优秀个体被保留的概率，而选择、交叉、变异等操作与基本遗传算法无异。

1. NSGA算法仍具有一定的缺点，主要体现在以下方面：

• （1）算法计算量大。NSGA算法的计算复杂度与种群数量N、目标函数个数m的关系为T = O(mN3)，当种群规模较大、目标函数较多时所耗时间较长。

• （2）没有应用精英策略。未通过精英策略提高优秀个体的保留概率，因而无法加快程序的执行速度。

• （3）需要人为地指定共享半径R，对于经验的要求非常高。

2. NSGA2算法主要在以下方面上做了改进：

• （1）NSGA-II算法使用了快速非支配排序法，将算法的计算复杂度由O(mN3)降到了O(mN2)，使得算法的计算时间大大减少。

• （2）采用了精英保留策略，将父代个体与子代个体合并后进行非支配排序，使得搜索空间变大，生成下一代父代种群时按顺序将优先级较高的个体选入，并在同级个体中采用拥挤度进行选择（排除较差的个体），保证了优秀个体能够有更大的概率被保留。

• （3）用拥挤度的方法代替了需指定共享半径的适应度共享策略，并作为在同级个体中选择优秀个体的标准，保证了种群中个体的多样性，有利于个体能够在整个区间内进行选择、交叉和变异。

3. 精英保留策略
   NSGA-II算法引入了精英保留策略，达到保留优秀个体淘汰劣等个体的目的。精英策略通过将父代与子代个体混合形成新的群体，扩大了产生下一代个体时的筛选范围。以图所示的例子进行分析，图中P表示父代种群，设其中的个体数量为n，Q表示子代种群，具体步骤如下：

• （1）将父代种群和子代种群合并形成新的种群。之后对新种群进行非支配排序，本例中将种群分成了6个Pareto等级。

• （2）进行新的父代的生成工作，先将Pareto等级为1的非支配个体放入新的父代集合当中，之后将Pareto等级为2的个体放入新的父代种群中，以此类推。

• （3）若等级为k的个体全部放入新的父代集合中后，集合中个体的数量小于n，而等级为k+1的个体全部放入新的父代集合中后，集合中的个体数量大于n，则对第k+1等级的全部个体计算拥挤度并将所有个体按拥挤度进行降序排列,之后将等级大于k+1的个体全部淘汰。本例中可以看出k为2，所以对Pareto等级为3的个体计算拥挤度并按其进行降序排序，等级为4~6的个体全部淘汰。

• （4） 将等级k+1中的个体按步骤2中排好的顺序逐个放入新的父代集合中，直到父代集合中的个体数量等于n，剩余的个体被淘汰。
  

2.NSGA2算法解决双目标优化问题实例

问题2：

#用NSGA2算法来解决双目标优化问题步骤

• 第一步：继承父类(ea.Problem)
• 第二步：调用父类的构造方法
• 第三步：创建目标函数。定义了目标函数evalVars，它重写了Problem类中的evalVars()。注意这个名字不能随便更改。
  Geatpy的Problem问题类提供两种目标函数的定义，分别是evalVars和aimFunc。前者（evalVars）是Geatpy2.7.0之后新增的写法，它传入决策变量矩阵Vars且需要返回对应的目标函数值矩阵ObjV和违反约束程度矩阵CV（若待求解的问题没有约束条件，则可以只返回目标函数矩阵）。后者（aimFunc）是传统的写法，它传入一个种群对象，且不需要返回值。
• 第四步：实例化类对象
• 第五步：调用optimize()函数来求解

用Geatpy工具中NSGA2算法解决问题2：

class MyProblem(ea.Problem):  # 继承Problem父类（geatpy封装好的类）
    def __init__(self):
        name = 'NSGA2算法'  # 初始化name（函数名称，可以随意设置）
        M = 2  # 优化目标个数（两个x)
        maxormins = [1] * M  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 1  # 初始化Dim（决策变量维数）
        varTypes = [0]  # 初始化varTypes（决策变量的类型，0：实数连续型变量；1：整数离散型变量）
        lb = [-10]  # 决策变量下界(自定义个上下界搜索)
        ub = [10]  # 决策变量上界
        lbin = [1]  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1]  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法（_init_）完成实例化，后跟参数
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def evalVars(self, Vars):  # 目标函数
        f1 = Vars ** 2 # 第一个目标函数
        f2 = (Vars - 2) ** 2 # 第二个目标函数
        ObjV = np.hstack([f1, f2])  # 计算目标函数值矩阵
        CV = -Vars ** 2 + 2.5 * Vars - 1.5  # 构建违反约束程度矩阵（需要转换为小于，反转一下）
        return ObjV, CV

# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(problem,
                                  # RI编码，种群个体100
                                    ea.Population(Encoding='RI', NIND=100),
                                    MAXGEN=200,  # 最大进化代数
                                    logTras=1 # 表示每隔多少代记录一次日志信息，0表示不记录。
                                    ) 
# 求解
res = ea.optimize(algorithm, seed=1, verbose=False, drawing=1, outputMsg=True, drawLog=False, saveFlag=False, dirName='result')

输出为：

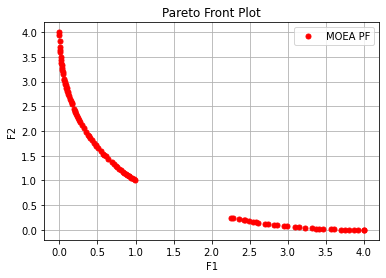
Execution time: 0.10509157180786133 s
Evaluation number: 20000
The number of non-dominated solutions is: 100
hv: 0.83201
spacing: 0.02100

三.多目标优化算法NSGA3

ZDT1、DTLZ1（DTLZ1—7）、WFG1，等等。以DTLZ1为例，可以通过ea.benchmarks.DTLZ1()直接实例化DTLZ1问题对象。用NSGA3算法求解DTLZ1的代码如下：

Geatpy2.7.0把已实现的测试问题归档进了benchmarks文件夹中，所以可以直接修改benchmarks后面的函数来测试某个问题

problem = ea.benchmarks.DTLZ1()  # 生成问题对象
# 构建算法
algorithm = ea.moea_NSGA3_templet(problem,
                                  ea.Population(Encoding='RI', NIND=100),
                                  MAXGEN=500,  # 最大进化代数。
                                  logTras=1)  # 表示每隔多少代记录一次日志信息，0表示不记录。
# 求解
res = ea.optimize(algorithm, verbose=True, drawing=1, outputMsg=True, drawLog=True, saveFlag=True, dirName='result')

输出为：

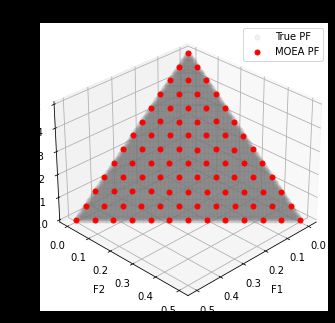
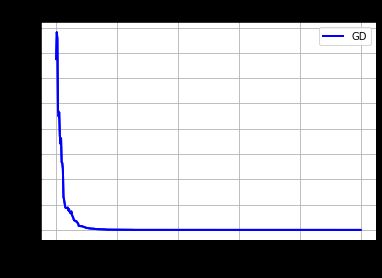
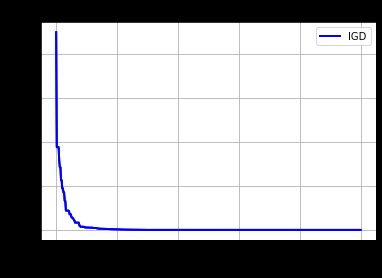
Execution time: 0.5562167167663574 s
Evaluation number: 45500
The number of non-dominated solutions is: 91
gd: 0.00020
igd: 0.02062
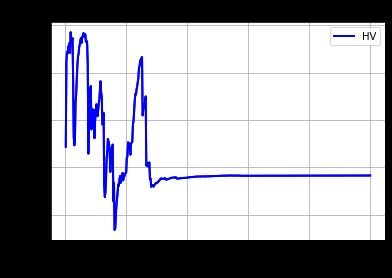
hv: 0.84156
spacing: 0.00028

---

总结

Geatpy工具：

• 进化算法介绍：http://geatpy.com/index.php/ea_introduction/
• Geatpy数据结构：http://geatpy.com/index.php/2020/10/19/2-geatpy%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%842-6-x/
• Geatpy案例：http://geatpy.com/index.php/demos/
• Geatpy工具中选择算子、重组算子、变异算子、多目标优化和多种群进化相关模块连接。