机器学习之算法优化—Geatpy工具中案例分析
案例分析
- 1.多种群进化优化案例
- 2.单目标优化案例
-
- 2.1例1是展示了一个带等式约束的连续型决策变量最大化目标的单目标优化问题的求解
- 2.2例2是展示了一个带约束的单目标旅行商问题的求解。
- 2.3例3是展示2个决策变量的单目标优化,决策变量的值将取自于一个设定好的变量集合
- 2.4例4是展示了一个需要混合编码种群来进化的最大化目标的单目标优化问题
- 3.双目标优化案例
-
- 3.1例1是展示了一个离散决策变量的最小化目标的双目标优化问题的求解
- 3.2例2是展示了一个带约束连续决策变量的最小化目标的双目标优化问题的求解
- 3.3例3是展示了一个带约束的多目标背包问题的求解
- 总结
1.多种群进化优化案例
问题1:如何用多种群来进行单目标优化
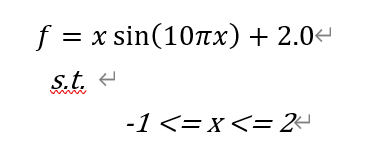
下面代码是通过加multi来构建SEGA进化算法来进行多种群进化优化:
# MyProblem.py
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Geatpy中已经封装好的Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [-1]*M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 1 # 初始化Dim(决策变量维数)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [-1] # 决策变量下界
ub = [2] # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, x): # 目标函数
f = x * np.sin(10 * np.pi * x) + 2.0
return f # 返回目标函数值
# main.py
from MyProblem import MyProblem # 导入自定义问题接口
import geatpy as ea # import geatpy
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 种群设置
Encoding = 'RI' # 编码方式(RI是实数整数混合编码)
NINDs = [5, 10, 15, 20] # 种群规模
population = [] # 创建种群列表
for i in range(len(NINDs)):
Field = ea.crtfld(Encoding,
problem.varTypes,
problem.ranges,
problem.borders) # 创建区域描述器。
population.append(ea.Population(
Encoding, Field, NINDs[i])) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化)。
# 构建算法
algorithm = ea.soea_multi_SEGA_templet(
problem, # 调用实例化问题对象
population, # 种群
MAXGEN=30, # 最大进化代数。
logTras=1, # 表示每隔多少代记录一次日志信息,0表示不记录。
trappedValue=1e-6, # 单目标优化陷入停滞的判断阈值。
maxTrappedCount=5) # 进化停滞计数器最大上限值。
# 求解
res = ea.optimize(algorithm,
verbose=True,
drawing=1,
outputMsg=True,
drawLog=False,
saveFlag=False,
# dirName='result'
)
print(res)
对上述代码创建种群中: 在实例化种群对象里面
import geatpy as ea
population = ea.Population(Encoding, Field, NIND),
NIND为所需要的个体数。
此时得到的population还没被真正初始化,仅仅是完成种群对象的实例化。
只有构造函数必须传入Chrom(种群染色体矩阵,每一行对应一个个体的一条染色体。),才算是完成种群真正的初始化。
因此一开始可以只传入Encoding, Field以及NIND来完成种群对象的实例化,
其他属性可以后面再通过计算进行赋值。
特殊用法1:
可以利用ea.Population(Encoding, Field, 0)来创建一个“空种群”,即不含任何个体的种群对象。
特殊用法2:
直接用ea.Population(Encoding)构建一个只包含编码信息的空种群。
Field : array - 译码矩阵,可以是FieldD或FieldDR(详见Geatpy数据结构)。 2.7.0版本之后,可以把问题类对象的varTypes、ranges、borders放到一个tuple中传入到此处, 即有Field = (varTypes, ranges, borders), 此时将调用crtfld自动构建Field。
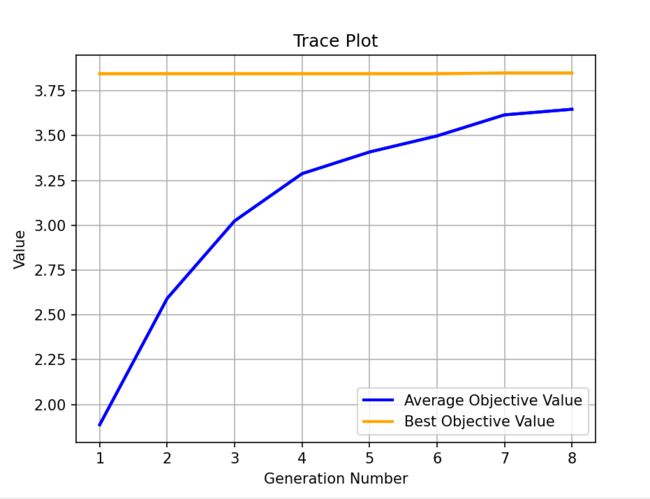
上述代码输出为:
==================================================================================
gen| eval | f_opt | f_max | f_avg | f_min | f_std
----------------------------------------------------------------------------------
0 | 50 | 3.84602E+00 | 3.84602E+00 | 1.88679E+00 | 4.99879E-02 | 8.47371E-01
1 | 100 | 3.84602E+00 | 3.84602E+00 | 2.59178E+00 | 1.99856E+00 | 5.29548E-01
2 | 150 | 3.84602E+00 | 3.84602E+00 | 3.02460E+00 | 2.35957E+00 | 3.80765E-01
3 | 202 | 3.84602E+00 | 3.84602E+00 | 3.28815E+00 | 2.35991E+00 | 2.22550E-01
4 | 253 | 3.84602E+00 | 3.84602E+00 | 3.40911E+00 | 2.47126E+00 | 1.97267E-01
5 | 304 | 3.84603E+00 | 3.84603E+00 | 3.49878E+00 | 2.47137E+00 | 1.90956E-01
6 | 355 | 3.84995E+00 | 3.84995E+00 | 3.61629E+00 | 3.43720E+00 | 7.95978E-02
7 | 405 | 3.84995E+00 | 3.84995E+00 | 3.64755E+00 | 3.61331E+00 | 7.39115E-02
- 添加multi的SEGA优化算法相对于SEGA算法就是对于种群 population创建的区别
2.单目标优化案例
2.1例1是展示了一个带等式约束的连续型决策变量最大化目标的单目标优化问题的求解
差分进化DE_rand_1_bin算法
算法描述:
- 本算法类实现的是经典的DE/rand/1/bin单目标差分进化算法。算法流程如下:
-
- 初始化候选解种群。
-
- 若满足停止条件则停止,否则继续执行。
-
- 对当前种群进行统计分析,比如记录其最优个体、平均适应度等等。
-
- 选择差分变异的基向量,对当前种群进行差分变异,得到变异个体。
-
- 将当前种群和变异个体合并,采用二项式分布交叉方法得到试验种群。
-
- 在当前种群和实验种群之间采用一对一生存者选择方法得到新一代种群。
-
- 回到第2步。
差分进化DE_rand_1_bin算法构造函数:
soea_DE_rand_1_bin_templet(problem, population, MAXGEN=None,
MAXTIME=None, MAXEVALS=None, MAXSIZE=None,
logTras=None, verbose=None, outFunc=None,
drawing=None, trappedValue=None, maxTrappedCount=None,
dirName=None, **kwargs)
主要参数说明:
problem:实例化问题对象
population:种群数量,int,默认None。
MAXSIZE:种群最大进化代数,int,默认None。
logTras:表示每隔多少代记录一次日志信息,0表示不记录。
代码为:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [-1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 3 # 初始化Dim(决策变量维数x1,x2,x3)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [0, 0, 0] # 决策变量下界
ub = [1, 1, 2] # 决策变量上界
lbin = [1, 1, 0] # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1, 1, 0] # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, Vars): # 目标函数
x1 = Vars[:, [0]]
x2 = Vars[:, [1]]
x3 = Vars[:, [2]]
f = 4 * x1 + 2 * x2 + x3 # 目标函数的值
# 采用可行性法则处理约束
CV = np.hstack( # hstack是水平顺序堆叠数组(按列)。
[2 * x1 + x2 - 1, x1 + 2 * x3 - 2, np.abs(x1 + x2 + x3 - 1)])
return f, CV
def calReferObjV(self): # 设定目标数参考值(本问题目标函数参考值设定为理论最优值)
referenceObjV = np.array([[2.5]])
return referenceObjV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.soea_DE_rand_1_bin_templet(
problem,
ea.Population(Encoding='RI', NIND=100),
MAXGEN=500, # 最大进化代数。
logTras=1) # 表示每隔多少代记录一次日志信息,0表示不记录。
algorithm.mutOper.F = 0.5 # 差分进化中的参数F
algorithm.recOper.XOVR = 0.7 # 重组概率
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
Execution time: 0.16287469863891602 s
Evaluation number: 50000
The best objective value is: 2.4999999999706057
The best variables are:
0.4999999999806069 2.8785119666729124e-11 0.49999999999060807
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the generation limit.', 'optPop': <geatpy.Population.Population object at 0x00000212B256D9D0>, 'lastPop': <geatpy.Population.Population object at 0x00000212B256D9A0>, 'Vars': array([[5.00000000e-01, 2.87851197e-11, 5.00000000e-01]]), 'ObjV': array([[2.5]]), 'CV': array([[-1.00011111e-11, -5.00000000e-01, 0.00000000e+00]]), 'executeTime': 0.16287469863891602, 'nfev': 50000, 'startTime': '2022-08-16 15h-56m-18s', 'endTime': '2022-08-16 15h-56m-18s'}
2.2例2是展示了一个带约束的单目标旅行商问题的求解。
import numpy as np
import geatpy as ea
import matplotlib.pyplot as plt
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 9 # 初始化Dim(决策变量维数B, C, D, E, F, G, H, I, J,9个城市)
varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [1] * Dim # 决策变量下界
ub = [9] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
# 新增一个属性存储旅行地坐标
self.places = np.array([[0.4, 0.4439], [0.2439, 0.1463],
[0.1707, 0.2293], [0.2293, 0.761],
[0.5171, 0.9414], [0.8732, 0.6536],
[0.6878, 0.5219], [0.8488, 0.3609],
[0.6683, 0.2536], [0.6195, 0.2634]])
def evalVars(self, x): # 目标函数
# 添加从0地出发且最后回到出发地
X = np.hstack(
[np.zeros((x.shape[0], 1)), x, np.zeros((x.shape[0], 1))]).astype(int)# astype转化为整型数据
ObjV = [] # 存储所有种群个体对应的总路程
for i in range(X.shape[0]):
journey = self.places[X[i], :] # 按既定顺序到达的地点坐标
distance = np.sum(np.sqrt(np.sum(np.diff(journey.T)**2, 0))) # 计算总路程
ObjV.append(distance)# ObjV列表在每次到达指定地点的循环中都添加distance总路程
f = np.array([ObjV]).T
# 找到违反约束条件的个体在种群中的索引,保存在向量exIdx中(如:若0、2、4号个体违反约束条件,则编程找出他们来)
exIdx1 = np.where(np.where(x == 3)[1] - np.where(x == 6)[1] < 0)[0]
exIdx2 = np.where(np.where(x == 4)[1] - np.where(x == 5)[1] < 0)[0]
exIdx = np.unique(np.hstack([exIdx1, exIdx2]))
CV = np.zeros((x.shape[0], 1))
CV[exIdx] = 1 # 把求得的违反约束程度矩阵赋值给种群pop的CV
# print(distance)
return f, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.soea_SEGA_templet(
problem,
# Encoding种群编码为P,NIND数量为50
ea.Population(Encoding='P', NIND=50),
MAXGEN=200, # 最大进化代数
logTras=1) # 表示每隔多少代记录一次日志信息,0表示不记录。
algorithm.mutOper.Pm = 0.5 # 变异概率
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
# matplotlib绘制路线图
if res['success']:
print('最短路程为:%s' % res['ObjV'][0][0])
print('最佳路线为:')
best_journey = np.hstack([0, res['Vars'][0, :], 0])
for i in range(len(best_journey)):
print(int(best_journey[i]), end=' ')
print()
# 绘图
plt.figure()
plt.plot(problem.places[best_journey.astype(int), 0],
problem.places[best_journey.astype(int), 1],
c='black')
plt.plot(problem.places[best_journey.astype(int), 0],
problem.places[best_journey.astype(int), 1],
'o',
c='black')
for i in range(len(best_journey)):
plt.text(problem.places[int(best_journey[i]), 0],
problem.places[int(best_journey[i]), 1],
chr(int(best_journey[i]) + 65),
fontsize=20)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('roadmap.svg', dpi=600, bbox_inches='tight')
plt.show()
else:
print('没找到可行解。')
Execution time: 0.26462340354919434 s
Evaluation number: 10000
The best objective value is: 2.778215287368279
The best variables are:
9 8 7 6 5 4 3 2 1
最短路程为:2.778215287368279
最佳路线为:
0 9 8 7 6 5 4 3 2 1 0
2.3例3是展示2个决策变量的单目标优化,决策变量的值将取自于一个设定好的变量集合
问题3:
max f = (-1+x1+((6-x2)*x2-2)*x2)**2+(-1+x1+((x2+2)*x2-10)*x2)**2
s.t.
x∈{1.1, 1, 0, 3, 5.5, 7.2, 9}(决策变量取值的集合)
代码为:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
self.var_set = np.array([1.1, 1, 0, 3, 5.5, 7.2, 9]) # 设定一个集合,要求决策变量的值取自于该集合
Dim = 2 # 初始化Dim(决策变量维数)
varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [0, 0] # 决策变量下界
ub = [6, 6] # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, Vars): # 目标函数
Vars = Vars.astype(np.int32) # 强制类型转换确保元素是整数
x1 = self.var_set[Vars[:, [0]]] # 得到所有的x1组成的列向量
x2 = self.var_set[Vars[:, [1]]] # 得到所有的x2组成的列向量
# 目标函数值
f = (-1 + x1 +((6 - x2) * x2 - 2) * x2)**2
+ (-1 + x1 + ((x2 + 2) * x2 - 10) * x2)**2
return f
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.soea_DE_rand_1_bin_templet(
problem, # 实例化问题对象
# 编码为RI,种群数量为20
ea.Population(Encoding='RI', NIND=20),
MAXGEN=25, # 最大进化代数。
logTras=1, # 表示每隔多少代记录一次日志信息,0表示不记录。
trappedValue=1e-6, # 单目标优化陷入停滞的判断阈值。
maxTrappedCount=10) # 进化停滞计数器最大上限值。
algorithm.mutOper.F = 0.5 # 差分进化中的参数F。
algorithm.recOper.XOVR = 0.2 # 差分进化中的参数Cr。
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
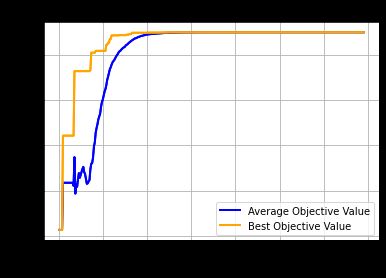
输出为:
==================================================================================
gen| eval | f_opt | f_max | f_avg | f_min | f_std
----------------------------------------------------------------------------------
0 | 20 | 8.00000E+00 | 7.16495E+05 | 1.10225E+05 | 8.00000E+00 | 2.11165E+05
1 | 40 | 8.00000E+00 | 7.08644E+05 | 8.95961E+04 | 8.00000E+00 | 2.12406E+05
2 | 60 | 0.00000E+00 | 7.08644E+05 | 7.39021E+04 | 0.00000E+00 | 2.11760E+05
3 | 80 | 0.00000E+00 | 7.08644E+05 | 7.38921E+04 | 0.00000E+00 | 2.11764E+05
4 | 100 | 0.00000E+00 | 2.95580E+04 | 3.02773E+03 | 0.00000E+00 | 8.78736E+03
5 | 120 | 0.00000E+00 | 2.95580E+04 | 1.55945E+03 | 0.00000E+00 | 6.42628E+03
6 | 140 | 0.00000E+00 | 6.66000E+02 | 8.32237E+01 | 0.00000E+00 | 1.95790E+02
7 | 160 | 0.00000E+00 | 6.66000E+02 | 4.42237E+01 | 0.00000E+00 | 1.44188E+02
8 | 180 | 0.00000E+00 | 5.96000E+02 | 3.39257E+01 | 0.00000E+00 | 1.29748E+02
9 | 200 | 0.00000E+00 | 5.96000E+02 | 3.36207E+01 | 0.00000E+00 | 1.29679E+02
10| 220 | 0.00000E+00 | 5.96000E+02 | 3.31207E+01 | 0.00000E+00 | 1.29795E+02
11| 240 | 0.00000E+00 | 6.03734E+01 | 3.42067E+00 | 0.00000E+00 | 1.30899E+01
Execution time: 0.004999637603759766 s
Evaluation number: 240
The best objective value is: 0.0
The best variables are:
1 2
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the trapped count limit.', 'optPop': <geatpy.Population.Population object at 0x0000018C8BB91520>, 'lastPop': <geatpy.Population.Population object at 0x0000018C8E42BFA0>, 'Vars': array([[1, 2]]), 'ObjV': array([[0.]]), 'CV': None, 'executeTime': 0.004999637603759766, 'nfev': 240, 'startTime': '2022-08-16 16h-50m-11s', 'endTime': '2022-08-16 16h-50m-11s'}
2.4例4是展示了一个需要混合编码种群来进化的最大化目标的单目标优化问题
问题4:
模型:
max f = sin(2x1) - cos(x2) + 2x3^2 -3x4 + (x5-3)^2 + 7x6
s.t.
-1.5 <= x1,x2 <= 2.5,
1 <= x3,x4,x5,x6 <= 7,且x3,x4,x5,x6为互不相等的整数。
分析:
该问题可以单纯用实整数编码’RI’来实现,但由于有一个”x3,x4,x5,x6互不相等“的约束,因此把x3,x4,x5,x6用排列编码’P’,x1和x2采用实整数编码’RI’来求解会更好。
代码为:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [-1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 6 # 初始化Dim(决策变量维数)
varTypes = [0, 0, 1, 1, 1,
1] # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [-1.5, -1.5, 1, 1, 1, 1] # 决策变量下界
ub = [2.5, 2.5, 7, 7, 7, 7] # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, X): # 目标函数
x1 = X[:, [0]] # 取X的第0列
x2 = X[:, [1]] # 取X的第1列
x3 = X[:, [2]] # 取X的第2列
x4 = X[:, [3]] # 取X的第3列
x5 = X[:, [4]] # 取X的第4列
x6 = X[:, [5]] # 取X的第5列
# 计算目标函数值
f = np.sin(2 * x1) - np.cos(x2) + 2 * x3**2 - 3 * x4 + (x5 - 3)**2 + 7 * x6
return f
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 快速构建算法
algorithm = ea.soea_psy_EGA_templet(
problem,# 种群
# 编码x1采用RI和x3,x4,x5,x6采用P,种群数量为40
ea.PsyPopulation(Encodings=['RI', 'P'],
NIND=40,
EncoIdxs=[[0, 1], [2, 3, 4, 5]]),
MAXGEN=25, # 最大进化代数
logTras=1) # 表示每隔多少代记录一次日志信息,0表示不记录。
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
Execution time: 0.012004852294921875 s
Evaluation number: 976
The best objective value is: 141.9129426887026
The best variables are:
0.8758544921875 -1.5 7.0 1.0 5.0 6.0
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the generation limit.', 'optPop': <geatpy.PsyPopulation.PsyPopulation object at 0x0000018C8E6AF8E0>, 'lastPop': <geatpy.PsyPopulation.PsyPopulation object at 0x0000018C8E50DBE0>, 'Vars': array([[ 0.87585449, -1.5 , 7. , 1. , 5. ,
6. ]]), 'ObjV': array([[141.91294269]]), 'CV': None, 'executeTime': 0.012004852294921875, 'nfev': 976, 'startTime': '2022-08-16 17h-30m-38s', 'endTime': '2022-08-16 17h-30m-38s'}
3.双目标优化案例
3.1例1是展示了一个离散决策变量的最小化目标的双目标优化问题的求解
问题1:
min f1 = -25 * (x1 - 2)**2 - (x2 - 2)**2 - (x3 - 1)**2 - (x4 - 4)**2 - (x5 - 1)**2
min f2 = (x1 - 1)**2 + (x2 - 1)**2 + (x3 - 1)**2 + (x4 - 1)**2 + (x5 - 1)**2
s.t.
x1 + x2 >= 2
x1 + x2 <= 6
x1 - x2 >= -2
x1 - 3*x2 <= 2
4 - (x3 - 3)**2 - x4 >= 0
(x5 - 3)**2 + x4 - 4 >= 0
x1,x2,x3,x4,x5 ∈ {0,1,2,3,4,5,6,7,8,9,10}
代码为:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self, M=2):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
Dim = 5 # 初始化Dim(决策变量维数)
maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数)
lb = [0] * Dim # 决策变量下界
ub = [10] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, Vars): # 目标函数
x1 = Vars[:, [0]]# 取Vars的第0列
x2 = Vars[:, [1]]
x3 = Vars[:, [2]]
x4 = Vars[:, [3]]
x5 = Vars[:, [4]]
f1 = -25 * (x1 - 2)**2 - (x2 - 2)**2 - (x3 - 1)**2 - (x4 - 4)**2 - (
x5 - 1)**2
f2 = (x1 - 1)**2 + (x2 - 1)**2 + (x3 - 1)**2 + (x4 - 1)**2 + (x5
- 1)**2
# # 利用罚函数法处理约束条件
# idx1 = np.where(x1 + x2 < 2)[0]
# idx2 = np.where(x1 + x2 > 6)[0]
# idx3 = np.where(x1 - x2 < -2)[0]
# idx4 = np.where(x1 - 3*x2 > 2)[0]
# idx5 = np.where(4 - (x3 - 3)**2 - x4 < 0)[0]
# idx6 = np.where((x5 - 3)**2 + x4 - 4 < 0)[0]
# exIdx = np.unique(np.hstack([idx1, idx2, idx3, idx4, idx5, idx6])) # 得到非可行解的下标
# f1[exIdx] = f1[exIdx] + np.max(f1) - np.min(f1)
# f2[exIdx] = f2[exIdx] + np.max(f2) - np.min(f2)
# 利用可行性法则处理约束条件
CV = np.hstack([
2 - x1 - x2,
x1 + x2 - 6,
-2 - x1 + x2,
x1 - 3 * x2 - 2, (x3 - 3)**2 + x4 - 4,
4 - (x5 - 3)**2 - x4
])
f = np.hstack([f1, f2])
return f, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(
problem,# 种群
# 编码为BG,种群数量为50
ea.Population(Encoding='BG', NIND=50),
MAXGEN=200, # 最大进化代数
logTras=0) # 表示每隔多少代记录一次日志信息,0表示不记录。
algorithm.mutOper.Pm = 0.2 # 修改变异算子的变异概率
algorithm.recOper.XOVR = 0.9 # 修改交叉算子的交叉概率
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
Execution time: 0.09539294242858887 s
Evaluation number: 10000
The number of non-dominated solutions is: 50
hv: 0.00000
spacing: 1775433830572192369529810102310722998484562153336328945664.00000
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the generation limit.', 'optPop': <geatpy.Population.Population object at 0x0000018C8E6AF520>, 'lastPop': <geatpy.Population.Population object at 0x0000018C8E6AF6D0>, 'Vars': array([[ 5, 1, 4, 0, 9],
......
[ -4, 0, -6, 0, -3, -32]]), 'executeTime': 0.09539294242858887, 'nfev': 10000, 'hv': 0.0, 'spacing': 1.7754338305721924e+57, 'startTime': '2022-08-16 17h-52m-13s', 'endTime': '2022-08-16 17h-52m-13s'}
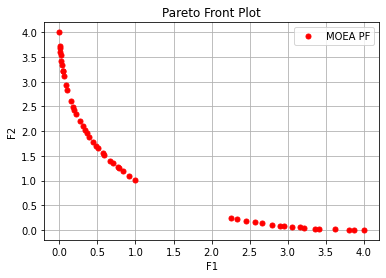
3.2例2是展示了一个带约束连续决策变量的最小化目标的双目标优化问题的求解
问题2:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self, M=2):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
Dim = 1 # 初始化Dim(决策变量维数)
maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数)
lb = [-10] * Dim # 决策变量下界
ub = [10] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, Vars): # 目标函数
f1 = Vars**2
f2 = (Vars - 2)**2
# # 利用罚函数法处理约束条件
# exIdx = np.where(Vars**2 - 2.5 * Vars + 1.5 < 0)[0] # 获取不满足约束条件的个体在种群中的下标
# f1[exIdx] = f1[exIdx] + np.max(f1) - np.min(f1)
# f2[exIdx] = f2[exIdx] + np.max(f2) - np.min(f2)
# 利用可行性法则处理约束条件
CV = -Vars**2 + 2.5 * Vars - 1.5
ObjV = np.hstack([f1, f2])
return ObjV, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(
problem,# 种群
# 编码为RI,种群数量为50
ea.Population(Encoding='RI', NIND=50),
MAXGEN=200, # 最大进化代数
logTras=0) # 表示每隔多少代记录一次日志信息,0表示不记录。
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
Execution time: 0.07406759262084961 s
Evaluation number: 10000
The number of non-dominated solutions is: 50
hv: 0.83042
spacing: 0.04844
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the generation limit.', 'optPop': <geatpy.Population.Population object at 0x0000018C8E6AF6A0>, 'lastPop': <geatpy.Population.Population object at 0x0000018C8BB1FF10>, 'Vars': array([[ 7.69700871e-01],
......
[-1.21446721e+00]]), 'executeTime': 0.07406759262084961, 'nfev': 10000, 'hv': 0.8304208517074585, 'spacing': 0.04844203363976716, 'startTime': '2022-08-16 18h-16m-10s', 'endTime': '2022-08-16 18h-16m-10s'}
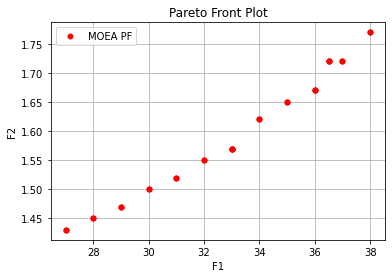
3.3例3是展示了一个带约束的多目标背包问题的求解
由上述问题中可以知道由于背包总质量不能超过92kg,则可以看似C ≤ 92 约束条件。方便后面目标函数的编写。
代码为:
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self, M=2):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
maxormins = [-1, 1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)
Dim = 5 # 初始化Dim(决策变量维数)
varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)
lb = [0] * Dim # 决策变量下界
ub = [3] * Dim # 决策变量上界
lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含)
ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含)
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
# 添加几个属性来存储P、R、C
self.P = np.array([[3, 4, 9, 15, 2], [4, 6, 8, 10, 2.5],
[5, 7, 10, 12, 3], [3, 5, 10, 10, 2]])
self.R = np.array([[0.2, 0.3, 0.4, 0.6,
0.1], [0.25, 0.35, 0.38, 0.45,
0.15], [0.3, 0.37, 0.5, 0.5, 0.2],
[0.3, 0.32, 0.45, 0.6, 0.2]])
self.C = np.array([[10, 13, 24, 32, 4], [12, 15, 22, 26, 5.2],
[14, 18, 25, 28, 6.8], [14, 14, 28, 32, 6.8]])
def evalVars(self, Vars): # 目标函数
x = Vars.astype(int) # 将Vars转化为整型
f1 = np.sum(self.P[x, [0, 1, 2, 3, 4]], 1)
f2 = np.sum(self.R[x, [0, 1, 2, 3, 4]], 1)
# 采用可行性法则处理约束(由上述可知质量不能超过92kg认为是约束条件)
CV = np.array([np.sum(self.C[x, [0, 1, 2, 3, 4]], 1)]).T - 92
ObjV = np.vstack([f1, f2]).T
return ObjV, CV
if __name__ == '__main__':
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(
problem,# 种群
# 编码为BG,种群数量为30
ea.Population(Encoding='BG', NIND=30),
MAXGEN=300, # 最大进化代数
logTras=0) # 表示每隔多少代记录一次日志信息,0表示不记录。
# 求解
res = ea.optimize(algorithm,verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True)
print(res)
Execution time: 0.11438202857971191 s
Evaluation number: 9000
The number of non-dominated solutions is: 30
hv: 0.09402
spacing: 0.00000
{'success': True, 'stopMsg': 'The algotirhm stepped because it exceeded the generation limit.', 'optPop': <geatpy.Population.Population object at 0x0000018C8E6D9880>, 'lastPop': <geatpy.Population.Population object at 0x0000018C8E6D9700>, 'Vars': array([[0, 0, 1, 1, 0],
......
[ -8. ]]), 'executeTime': 0.11438202857971191, 'nfev': 9000, 'hv': 0.09401778876781464, 'spacing': 0.0, 'startTime': '2022-08-16 18h-23m-21s', 'endTime': '2022-08-16 18h-23m-21s'}
总结
Geatpy工具中进化算法结合其它算法有:
k-means聚类:https://github.com/geatpy-dev/geatpy/tree/master/demo/soea_demo/soea_demo8
用进化算法+多进程/多线程来搜索SVM:https://github.com/geatpy-dev/geatpy/tree/master/demo/soea_demo/soea_demo6