机器学习算法--多元线性回归模型

将一元线性回归模型推广到多个解释变量，这个过程叫作多元线性回归：

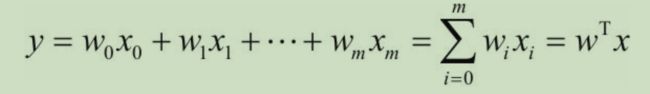
现用数据集中的所有变量来训练多元回归模型：

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RANSACRegressor
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import scipy as sp
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error

df = pd.read_csv('xxx\\housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
              'NOX', 'RM', 'AGE', 'DIS', 'RAD',
              'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
print(df.head())
X = df.iloc[:, :-1].values
y = df['MEDV'].values

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=0)

slr = LinearRegression()

slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)

plt.scatter(y_train_pred,  y_train_pred - y_train,
            c='steelblue', marker='o', edgecolor='white',
            label='Training data')
plt.scatter(y_test_pred,  y_test_pred - y_test,
            c='limegreen', marker='s', edgecolor='white',
            label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')  # 残差
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10, 50])
plt.tight_layout()

# plt.savefig('images/10_09.png', dpi=300)
plt.show()
# MSE
# 过拟合
print('MSE train: %.3f, test: %.3f' % (
        mean_squared_error(y_train, y_train_pred),
        mean_squared_error(y_test, y_test_pred)))

# 报告决定系数（R2）可能更有用，可以把这理解为MSE的标准版，目的是为更好地解释模型的性能，
# 决定系数反应了y的波动有多少百分比能被x的波动所描述，即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释。
# 拟合优度越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
print('R^2 train: %.3f, test: %.3f' % (
        r2_score(y_train, y_train_pred),
        r2_score(y_test, y_test_pred)))