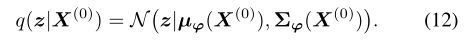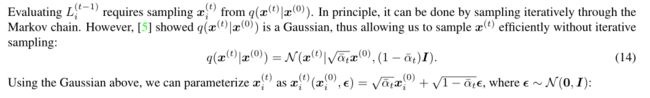声明
- 本博客仅仅是为了记录学习过程。
- 作者:jiadeChen
点云生成的扩散概率模型

train_gen代码阅读
- 在这一部分将会对train_gen.py的主要部分进行阅读,大致按照整个代码的执行流程来完成代码的阅读。
argparse代码的全局参数
- 当后面出现不清楚的参数的时候可以过来查看,一般采用默认参数。
parser = argparse.ArgumentParser()
parser.add_argument('--model', type=str, default='flow', choices=['flow', 'gaussian'])
parser.add_argument('--latent_dim', type=int, default=256)
parser.add_argument('--num_steps', type=int, default=100)
parser.add_argument('--beta_1', type=float, default=1e-4)
parser.add_argument('--beta_T', type=float, default=0.02)
parser.add_argument('--sched_mode', type=str, default='linear')
parser.add_argument('--flexibility', type=float, default=0.0)
parser.add_argument('--truncate_std', type=float, default=2.0)
parser.add_argument('--latent_flow_depth', type=int, default=14)
parser.add_argument('--latent_flow_hidden_dim', type=int, default=256)
parser.add_argument('--num_samples', type=int, default=4)
parser.add_argument('--sample_num_points', type=int, default=2048)
parser.add_argument('--kl_weight', type=float, default=0.001)
parser.add_argument('--residual', type=eval, default=True, choices=[True, False])
parser.add_argument('--spectral_norm', type=eval, default=False, choices=[True, False])
parser.add_argument('--dataset_path', type=str, default='./data/shapenet.hdf5')
parser.add_argument('--categories', type=str_list, default=['airplane'])
parser.add_argument('--scale_mode', type=str, default='shape_unit')
parser.add_argument('--train_batch_size', type=int, default=128)
parser.add_argument('--val_batch_size', type=int, default=64)
parser.add_argument('--lr', type=float, default=2e-3)
parser.add_argument('--weight_decay', type=float, default=0)
parser.add_argument('--max_grad_norm', type=float, default=10)
parser.add_argument('--end_lr', type=float, default=1e-4)
parser.add_argument('--sched_start_epoch', type=int, default=200 * THOUSAND)
parser.add_argument('--sched_end_epoch', type=int, default=400 * THOUSAND)
parser.add_argument('--seed', type=int, default=2020)
parser.add_argument('--logging', type=eval, default=True, choices=[True, False])
parser.add_argument('--log_root', type=str, default='./logs_gen')
parser.add_argument('--device', type=str, default='cuda')
parser.add_argument('--max_iters', type=int, default=float('inf'))
parser.add_argument('--val_freq', type=int, default=1000)
parser.add_argument('--test_freq', type=int, default=30 * THOUSAND)
parser.add_argument('--test_size', type=int, default=400)
parser.add_argument('--tag', type=str, default=None)
args = parser.parse_args()
model的创建
- 由于
arg.model参数默认是flow,并且在论文的点云生成实现部分作者也提到,采用一系列的normalizing flow。
logger.info('Building model...')
if args.model == 'gaussian':
model = GaussianVAE(args).to(args.device)
elif args.model == 'flow':
model = FlowVAE(args).to(args.device)
logger.info(repr(model))
if args.spectral_norm:
add_spectral_norm(model, logger=logger)
main loop
- 下面就是整个train_gen.py的主要循环流程,
arg.max_iters默认为inf,因此这个训练是迭代无限次,直到ctrl+C中断程序执行。
- 在每一轮迭代时会首先调用
train(it)进行训练,然后在满足特定条件下会进行验证(validate)和测试(test)。
- 由于主要关注训练(train)过程,因此主要看train,至于validate_inspect和test之后有机会再看。
logger.info('Start training...')
try:
it = 1
while it <= args.max_iters:
train(it)
if it % args.val_freq == 0 or it == args.max_iters:
validate_inspect(it)
opt_states = {
'optimizer': optimizer.state_dict(),
'scheduler': scheduler.state_dict(),
}
ckpt_mgr.save(model, args, 0, others=opt_states, step=it)
if it % args.test_freq == 0 or it == args.max_iters:
test(it)
it += 1
except KeyboardInterrupt:
logger.info('Terminating...')
train方法(调用模型进行训练)
- 首先作者使用
yield关键字实现了DataLoader的迭代,具体请查阅get_data_iterator函数,因此每一轮训练可以使用next()获取训练数据,那么训练点云x的shape为(batch_size, num_point, channels),具体的就是(128, 2048, 3),也就是128个点云,每个点云2048个点。
optimizer.zero_grad()重置梯度,防止上一次训练时的梯度影响当前的训练过程。具体可以参考官网zero_grad。model.train()将模型设置为训练阶段,具体可以参考nn.Module.trainargs.spectral_norm默认是False,这里应该是调用特殊的初始化函数对网络的参数初始化(猜测,并没有看)- 之后就是关键的forward过程,kl_weight默认是0.001,调用model的get_loss方法。
- 之后就是loss的后向传播与梯度下降,还有就是使用SummaryWriter保存训练过程当中的一些信息。
- 下面主要来说一下FlowVAE,也就是点云生成当中主要的网络模型
def train(it):
batch = next(train_iter)
x = batch['pointcloud'].to(args.device)
optimizer.zero_grad()
model.train()
if args.spectral_norm:
spectral_norm_power_iteration(model, n_power_iterations=1)
kl_weight = args.kl_weight
loss = model.get_loss(x, kl_weight=kl_weight, writer=writer, it=it)
loss.backward()
orig_grad_norm = clip_grad_norm_(model.parameters(), args.max_grad_norm)
optimizer.step()
scheduler.step()
logger.info('[Train] Iter %04d | Loss %.6f | Grad %.4f | KLWeight %.4f' % (
it, loss.item(), orig_grad_norm, kl_weight
))
writer.add_scalar('train/loss', loss, it)
writer.add_scalar('train/kl_weight', kl_weight, it)
writer.add_scalar('train/lr', optimizer.param_groups[0]['lr'], it)
writer.add_scalar('train/grad_norm', orig_grad_norm, it)
writer.flush()
FlowVAE
- FlowVAE主要的就是
__init__,get_loss,sample
- args:这个就是前面开篇提到的全局参数
- encoder:采用PointNetEncoder,具体的可以参照论文的如下部分

- 使用编码器的原因:论文前面也提到了,使用encoder将输入点云 X ( 0 ) X^{(0)} X(0)编码为latent code z的分布,同时获得 μ ϕ μ_ϕ μϕ与 ∑ ϕ ∑_ϕ ∑ϕ
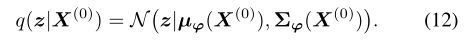
- flow:这个就是论文中提到的一系列affine coupling layers,这个flow在传播的时候分为正向传播和反向传播,实现分布latent code z与分布w之间的转换。在训练过程当中z->w,在采样过程当中w->z,其中w~N(0,I)。关于affine coupling layers是如何实现方便计算雅克比行列式与可逆的,可以参照,知乎:affine coupling layers部分。
- diffusion:具体的实例为DiffusionPoint,这个DiffusionPoint主要是包含两个参数
net和var_sched(可以先看后面DiffusionPoint的讲解之后再来看这一部分)。
get_loss
- 首先使用encoder(这里就是PointNetEncoder)对输入点云 X ( 0 ) {X^{(0)}} X(0)进行编码,得到 μ ϕ {\mu_{\phi}} μϕ与 Σ ϕ {\Sigma_{\phi}} Σϕ(其实并不是真正的方差,这里是一个logvariance,因为使用方差恒大于0需要激活函数,而logvariance可正可负不需要激活函数),也就是z_mu,z_sigma,他们的shape都是(128,256)。
- 之后是一个重参数化,从正态分布当中采样一个 ϵ {\epsilon} ϵ,那么 Σ ϵ + μ {\Sigma\epsilon}+{\mu} Σϵ+μ也是正态分布,并且方差是 Σ {\Sigma} Σ,均值是 μ {\mu} μ,这样可以保证 Σ {\Sigma} Σ与 μ {\mu} μ可以由神经网络进行学习,而 ϵ {\epsilon} ϵ仅仅是一个常数而已。
- 然后通过z计算高斯分布的微分熵(对连续性随机变量的概率分布中的不确定性总量进行量化),可以参考公式高斯分布微分熵。
- 然后调用由一系列affine coupling layers构成的normalizing flow将latent z转化为w(w是一个高维正态分布),因为正向扩散表示从desired distribution到noise distribution,反向是由noise distribution得到desired distribution,因此reverse参数是False。(具体的normaling flow可以参照后面的阅读)
- 之后就是通过
standard_normal_logprob得到w的概率密度函数的对数,可以参考改为正态分布的概率密度函数。高维正态分布概率密度函数相关
- 之后就是根据分布变换公式,将log_pw-delta_log_pw就可以得到log_pz。
neg_elbo = self.diffusion.get_loss(x, z)可以参考DiffusionPoint当中的相关内容。- 后面呢就是计算整体的损失函数,但是数学功底和机器学习当中的ELBO先关知识有点欠缺,等学会了再来填坑。
sample
- 这里给一篇相同的这篇论文代码解读的博客,相关博客。在这篇博客当中将sample过程定义为推断过程,但是博主关于变分推断等相关知识比较欠缺,目前还不理解,等理解了再来填坑。
- 其实这个方法是test_gen当中会调用的。
- w:就是高斯噪声,由randn随机生成的。
- num_points:是表示每个点云要生成的点的数目,或者说是每个点云包含的点的数目。
- 那么采样其实也就是markov chain的逆向过程,markov chain是由有意点云变化为噪声点云,那么逆向过程就是相反的。
- 首先将高斯噪声w通过affine coupling layers逆向传播,获得latent distribution z。
- 然后从latent distribution z当中采样,具体的采样可以参照DiffusionPoint。
class FlowVAE(Module):
def __init__(self, args):
super().__init__()
self.args = args
self.encoder = PointNetEncoder(args.latent_dim)
self.flow = build_latent_flow(args)
self.diffusion = DiffusionPoint(
net=PointwiseNet(point_dim=3, context_dim=args.latent_dim, residual=args.residual),
var_sched=VarianceSchedule(
num_steps=args.num_steps,
beta_1=args.beta_1,
beta_T=args.beta_T,
mode=args.sched_mode
)
)
def get_loss(self, x, kl_weight, writer=None, it=None):
"""
Args:
x: Input point clouds, (B, N, d).
"""
batch_size, _, _ = x.size()
z_mu, z_sigma = self.encoder(x)
z = reparameterize_gaussian(mean=z_mu, logvar=z_sigma)
entropy = gaussian_entropy(logvar=z_sigma)
w, delta_log_pw = self.flow(z, torch.zeros([batch_size, 1]).to(z), reverse=False)
log_pw = standard_normal_logprob(w).view(batch_size, -1).sum(dim=1, keepdim=True)
log_pz = log_pw - delta_log_pw.view(batch_size, 1)
neg_elbo = self.diffusion.get_loss(x, z)
loss_entropy = -entropy.mean()
loss_prior = -log_pz.mean()
loss_recons = neg_elbo
loss = kl_weight * (loss_entropy + loss_prior) + neg_elbo
if writer is not None:
writer.add_scalar('train/loss_entropy', loss_entropy, it)
writer.add_scalar('train/loss_prior', loss_prior, it)
writer.add_scalar('train/loss_recons', loss_recons, it)
writer.add_scalar('train/z_mean', z_mu.mean(), it)
writer.add_scalar('train/z_mag', z_mu.abs().max(), it)
writer.add_scalar('train/z_var', (0.5 * z_sigma).exp().mean(), it)
return loss
def sample(self, w, num_points, flexibility, truncate_std=None):
batch_size, _ = w.size()
if truncate_std is not None:
w = truncated_normal_(w, mean=0, std=1, trunc_std=truncate_std)
z = self.flow(w, reverse=True).view(batch_size, -1)
samples = self.diffusion.sample(num_points, context=z, flexibility=flexibility)
return samples
DiffusionPoint
- 为了方便,在这里说明一下FlowVAE在构造DiffusionPoint时候设置的一些参数。
net=PointwiseNet,var_sched=VarianceSchedule。
- 可以先看后面的,PointwiseNet和VarianceSchedule的阅读,再来看这个(递归阅读哈哈哈)。
get_loss
- 这里是通过初始点云 X ( 0 ) {X^{(0)}} X(0)与context来获得ELBO。但是为什么ELBO的计算变成了一个MSE_LOSS目前还没有搞清楚,等搞清楚了回来填坑。
- 在FlowVAE的get_loss方法中调用DiffusionPoint的get_loss方法获取ELBO(源代码中的注释为Negative ELBO of P(X|z))。

- 首先就是在[1, num_step]当中随机采样步数(也就是相当于随机采样时间t)。
- 然后根据采样的时间t,获取对应时刻的 β {\beta} β与 α ‾ t {\overline{\alpha}_{t}} αt
- 为了说明 c 0 {c_{0}} c0与 c 1 {c_{1}} c1的作用,下面将论文付件当中的说明贴出来。
- 这个是Diffusion Probabilistic Models for 3D Point Cloud Generation的附件中的说明,那么说明中提到的[5]论文相关论文连接,当中的相关内容我也放在下面。
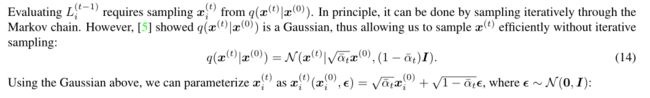
- 下面这个是付件中提到的[5]这篇论文,也就是Denoising Diffusion Probabilistic Models这一篇当中的相关内容。

- 其实大致意思就是说原则上应该是从markov chain当中迭代进行采样的,但是根据 q ( x ( t ) ∣ x ( 0 ) ) = N ( x ( t ) ∣ α ‾ t x ( 0 ) , ( 1 − α ‾ t ) I ) {q(x^{(t)}|x^{(0)})=N(x^{(t)}|{\sqrt{\overline{\alpha}_{t}}{x^{(0)}}, {(1-\overline{\alpha}_{t})}I})} q(x(t)∣x(0))=N(x(t)∣αt x(0),(1−αt)I),我们就不用迭代采样了,只需要 x i ( t ) = α ‾ t x ( 0 ) + 1 − α ‾ t ϵ , ϵ ∼ N ( 0 , I ) {x_{i}^{(t)}=\sqrt{\overline{\alpha}_{t}}{x^{(0)}}+{\sqrt{1-\overline{\alpha}_{t}}{\epsilon}}},{{\epsilon}{\sim}N(0, I)} xi(t)=αt x(0)+1−αt ϵ,ϵ∼N(0,I)。
- 上面的过程跟重采样有点类似。
- 这样 c 0 ∗ x 0 + c 1 ∗ e r a n d {c_{0} * x_{0} + c_{1} * e_{rand}} c0∗x0+c1∗erand其实就是每个时间点t对应的点的位置。
- 那么为什么要将 c 0 ∗ x 0 + c 1 ∗ e r a n d {c_{0} * x_{0} + c_{1} * e_{rand}} c0∗x0+c1∗erand放到self.net也就是PointwiseNet当中进行学习呢,由于PointwiseNet是由ConcatSquashLinear组成的,实际上参照付件当中的内容作者是将Reverse Diffusion Kernel建模为一些列的concatsquash layers。
- 后面就是将反向扩散后的点云与 e r a n d e_{rand} erand求一个mse_loss,但是为什么要这么做还不清楚,等搞清楚了再来填坑。
sample
- 这个方法从latent distribution z当中迭代采样点云。其实主要就是markov kernel添加噪声的逆向过程。

- 论文中提到 μ θ {\mu_{\theta}} μθ是被 θ {\theta} θ参数化的神经网络学习到的。
- x n e x t = c 0 ∗ ( x t − c 1 ∗ e t h e t a ) + σ ∗ z {x_{next} = c_0 * (x_t - c_1 * e_{theta}) + \sigma * z} xnext=c0∗(xt−c1∗etheta)+σ∗z,就可以看出来了, σ {\sigma} σ是方差,而 x n e x t = c 0 ∗ ( x t − c 1 ∗ e t h e t a ) + σ ∗ z {x_{next} = c_0 * (x_t - c_1 * e_{theta}) + \sigma * z} xnext=c0∗(xt−c1∗etheta)+σ∗z应该就是 μ θ {\mu_{\theta}} μθ
class DiffusionPoint(Module):
def __init__(self, net, var_sched: VarianceSchedule):
"""
Args:
net: PointWiseNet
var_sched: VarianceSchedule
"""
super().__init__()
self.net = net
self.var_sched = var_sched
def get_loss(self, x_0, context, t=None):
"""
Args:
x_0: Input point cloud, (B, N, d).
context: Shape latent, (B, F).
"""
batch_size, _, point_dim = x_0.size()
if t == None:
t = self.var_sched.uniform_sample_t(batch_size)
alpha_bar = self.var_sched.alpha_bars[t]
beta = self.var_sched.betas[t]
c0 = torch.sqrt(alpha_bar).view(-1, 1, 1)
c1 = torch.sqrt(1 - alpha_bar).view(-1, 1, 1)
e_rand = torch.randn_like(x_0)
e_theta = self.net(c0 * x_0 + c1 * e_rand, beta=beta, context=context)
loss = F.mse_loss(e_theta.view(-1, point_dim), e_rand.view(-1, point_dim), reduction='mean')
return loss
def sample(self, num_points, context, point_dim=3, flexibility=0.0, ret_traj=False):
batch_size = context.size(0)
x_T = torch.randn([batch_size, num_points, point_dim]).to(context.device)
traj = {self.var_sched.num_steps: x_T}
for t in range(self.var_sched.num_steps, 0, -1):
z = torch.randn_like(x_T) if t > 1 else torch.zeros_like(x_T)
alpha = self.var_sched.alphas[t]
alpha_bar = self.var_sched.alpha_bars[t]
sigma = self.var_sched.get_sigmas(t, flexibility)
c0 = 1.0 / torch.sqrt(alpha)
c1 = (1 - alpha) / torch.sqrt(1 - alpha_bar)
x_t = traj[t]
beta = self.var_sched.betas[[t] * batch_size]
e_theta = self.net(x_t, beta=beta, context=context)
x_next = c0 * (x_t - c1 * e_theta) + sigma * z
traj[t - 1] = x_next.detach()
traj[t] = traj[t].cpu()
if not ret_traj:
del traj[t]
if ret_traj:
return traj
else:
return traj[0]
VarianceSchedule
- 这个VarianceSchedule类应该就是variance schedule hyper-parameters,也就是论文中高斯分布中与均值和协方差有关系的参数β。
init
- num_step:默认为100,猜测应该是markov chain的长度
- beta_1,beta_T:β的开始值与结束值。
- mode:虽然可以传参控制mode的类型,但是他这里使用assert断言mode只能是linear,也就是线性的生成β序列。可以参考linspace。
- betas:[0, beta_1, …, beta_T],长度为101。
- alphas:1-betas。
- alpha_bars:某个时间t时,alphas的叠乘,这里取了对数,将乘法转化为加法,然后有做了exp,得到叠乘。
- sigmas_flex: β \sqrt{\beta} β 。
- sigmas_inflex: 1 − α ‾ t − 1 1 − α ‾ t β t \sqrt{\frac{1-\overline\alpha_{t-1}}{1-\overline\alpha_{t}}{\beta_{t}}} 1−αt1−αt−1βt ,猜测应该是 γ t \gamma_{t} γt的开方。
- 之后就是使用register_buffer保存(可以不参与梯度下降),参考官方文档register_buffer。
class VarianceSchedule(Module):
def __init__(self, num_steps, beta_1, beta_T, mode='linear'):
"""
Args:
num_steps: 100
beta_1: 1e-4
beta_T: 0.02
"""
super().__init__()
assert mode in ('linear',)
self.num_steps = num_steps
self.beta_1 = beta_1
self.beta_T = beta_T
self.mode = mode
if mode == 'linear':
betas = torch.linspace(beta_1, beta_T, steps=num_steps)
betas = torch.cat([torch.zeros([1]), betas], dim=0)
alphas = 1 - betas
log_alphas = torch.log(alphas)
for i in range(1, log_alphas.size(0)):
log_alphas[i] += log_alphas[i - 1]
alpha_bars = log_alphas.exp()
sigmas_flex = torch.sqrt(betas)
sigmas_inflex = torch.zeros_like(sigmas_flex)
for i in range(1, sigmas_flex.size(0)):
sigmas_inflex[i] = ((1 - alpha_bars[i - 1]) / (1 - alpha_bars[i])) * betas[i]
sigmas_inflex = torch.sqrt(sigmas_inflex)
self.register_buffer('betas', betas)
self.register_buffer('alphas', alphas)
self.register_buffer('alpha_bars', alpha_bars)
self.register_buffer('sigmas_flex', sigmas_flex)
self.register_buffer('sigmas_inflex', sigmas_inflex)
def uniform_sample_t(self, batch_size):
ts = np.random.choice(np.arange(1, self.num_steps + 1), batch_size)
return ts.tolist()
def get_sigmas(self, t, flexibility):
assert 0 <= flexibility and flexibility <= 1
sigmas = self.sigmas_flex[t] * flexibility + self.sigmas_inflex[t] * (1 - flexibility)
return sigmas
PointwiseNet
PointwiseNet以及后面的concatsquash layers有啥用

init
- act:激活函数采用了leaky_relu,参考文档leaky_relu。
- residual:默认为True。
- layers:是一组ConcatSquanshLinear(可以看后面)。
forward
- x:输入的点云,(batch_size, num_point, channels)也就是(128, 2048, 3)。
- beta:hpyer-parameter
- context:这里的content应该就是latent z
- 首先调整β与context的shape,再在context上添加 β \beta β, sin β \sin{\beta} sinβ, cos β \cos{\beta} cosβ得到ctx_emb。
- 之后就是调用self.layers中的ConcatSquashLinear实例对out进行调整,ConcatSquashLinear中的layer(x) * gate + bias,由于residual默认为True,返回x+out。
class PointwiseNet(Module):
def __init__(self, point_dim, context_dim, residual):
super().__init__()
self.act = F.leaky_relu
self.residual = residual
self.layers = ModuleList([
ConcatSquashLinear(3, 128, context_dim + 3),
ConcatSquashLinear(128, 256, context_dim + 3),
ConcatSquashLinear(256, 512, context_dim + 3),
ConcatSquashLinear(512, 256, context_dim + 3),
ConcatSquashLinear(256, 128, context_dim + 3),
ConcatSquashLinear(128, 3, context_dim + 3)
])
def forward(self, x, beta, context):
"""
Args:
x: Point clouds at some timestep t, (B, N, d).
beta: Time. (B, ).
context: Shape latents. (B, F).
"""
batch_size = x.size(0)
beta = beta.view(batch_size, 1, 1)
context = context.view(batch_size, 1, -1)
time_emb = torch.cat([beta, torch.sin(beta), torch.cos(beta)], dim=-1)
ctx_emb = torch.cat([time_emb, context], dim=-1)
out = x
for i, layer in enumerate(self.layers):
out = layer(ctx=ctx_emb, x=out)
if i < len(self.layers) - 1:
out = self.act(out)
if self.residual:
return x + out
else:
return out
ConcatSquanshLinear
作用

init
- dim_in,dim_out:输入维度与输出维度。
- dimctx:args中默认latent code z的维度为256,这里dimctx应该是256+3,+3是因为前面PointwiseNet调用之前对dimctx进行了concat操作。
- _layer:Linear
- _hyper_gate:
- _hyper_bias:
- 最后返回是_layer(x) * gate + bias,具体作用就是参照付件当中的反向扩散核。
class ConcatSquashLinear(Module):
def __init__(self, dim_in, dim_out, dim_ctx):
super(ConcatSquashLinear, self).__init__()
self._layer = Linear(dim_in, dim_out)
self._hyper_bias = Linear(dim_ctx, dim_out, bias=False)
self._hyper_bias = Linear(dim_ctx, dim_out)
def forward(self, ctx, x):
gate = torch.sigmoid(self._hyper_gate(ctx))
bias = self._hyper_bias(ctx)
ret = self._layer(x) * gate + bias
return ret
normalizing flow
build
- 根据args当中标注的,latent_flow_depth默认为14。
- 可以看出来实际上就是家里一系列的affine coupling layers
- latent_dim与latent_flow_hidden_dim默认均为256。
def build_latent_flow(args):
chain = []
for i in range(args.latent_flow_depth):
chain.append(CouplingLayer(args.latent_dim, args.latent_flow_hidden_dim, swap=(i % 2 == 0)))
return SequentialFlow(chain)
affine coupling layers
- 如果看了前面提到的affine coupling layers当中的补充内容仿射耦合层,应该知道仿射耦合的核心就是将输入划分为两个部分a、b,其中b送入神经网络增强得到参数s与t,之后令a=s⊙a+t,最后将a与b拼接就完成了一个仿射耦合层的运算。
init
- d:latent_dim默认为256,d-(d//2)表示就是输入的一半,对输入进行划分。
- intermediate_dim:是latent_flow_hidden_dim默认为256。
- swap:根据当前是奇偶进行设置,是否将均分的a、b两个部分进行交换。
- net_s_t:就是将a、b中某一部分进行加强的神经网络,输出s_t为(128,256)
forward
- x:实际上是在某个时刻t所对应的latent distribution。
- logpx:初始为全0张量,(batch_size, 1)。
- in_dim、out_dim均为128,x.shape[1]为256.
- 将前半部分送入神经网络强化,得到s_t为(128, 256)维度。
- scale就是s,shift就是t,维度都是(batch_size, 128)
- logdetjac就是雅克比行列式的对数,按照上面知乎的参考资料就是s乘积的对数,这里的logdetjac应该是用于后面的对数似然。
- 后面就涉及到正向与反向传播的问题了,是有z->w还是w->z。
- 最后返回的是当前变换后的latent dsitribution与logpx+delta_logp(最后整个flow执行完成就是获得整个雅克比乘积的对数)。
class CouplingLayer(nn.Module):
def __init__(self, d, intermediate_dim, swap=False):
nn.Module.__init__(self)
self.d = d - (d // 2)
self.swap = swap
self.net_s_t = nn.Sequential(
nn.Linear(self.d, intermediate_dim),
nn.ReLU(inplace=True),
nn.Linear(intermediate_dim, intermediate_dim),
nn.ReLU(inplace=True),
nn.Linear(intermediate_dim, (d - self.d) * 2),
)
def forward(self, x, logpx=None, reverse=False):
if self.swap:
x = torch.cat([x[:, self.d:], x[:, :self.d]], 1)
in_dim = self.d
out_dim = x.shape[1] - self.d
s_t = self.net_s_t(x[:, :in_dim])
scale = torch.sigmoid(s_t[:, :out_dim] + 2.)
shift = s_t[:, out_dim:]
logdetjac = torch.sum(torch.log(scale).view(scale.shape[0], -1), 1, keepdim=True)
if not reverse:
y1 = x[:, self.d:] * scale + shift
delta_logp = -logdetjac
else:
y1 = (x[:, self.d:] - shift) / scale
delta_logp = logdetjac
y = torch.cat([x[:, :self.d], y1], 1) if not self.swap else torch.cat([y1, x[:, :self.d]], 1)
if logpx is None:
return y
else:
return y, logpx + delta_logp
SequentialFlow
init
- 就是将构造好的markov chain转化为ModuleList。
forward
- x:是刚刚用reparameterize_gaussian获得的latent z。
- logpx:是全0的张量,(batch_size, 1)。
- reverse:由于是markov的正向传播,就是False了。
- inds:None
- 然后调用makov chain进行前向传播。
class SequentialFlow(nn.Module):
"""A generalized nn.Sequential container for normalizing flows.
"""
def __init__(self, layersList):
super(SequentialFlow, self).__init__()
self.chain = nn.ModuleList(layersList)
def forward(self, x, logpx=None, reverse=False, inds=None):
if inds is None:
if reverse:
inds = range(len(self.chain) - 1, -1, -1)
else:
inds = range(len(self.chain))
if logpx is None:
for i in inds:
x = self.chain[i](x, reverse=reverse)
return x
else:
for i in inds:
x, logpx = self.chain[i](x, logpx, reverse=reverse)
return x, logpx