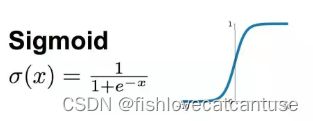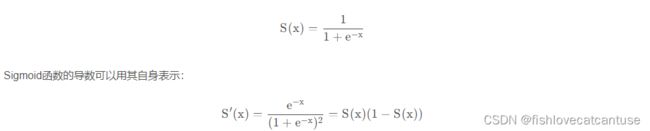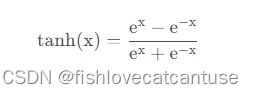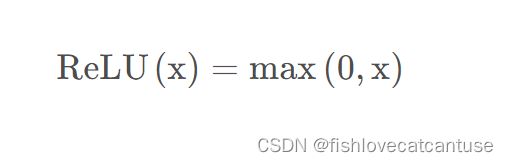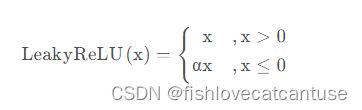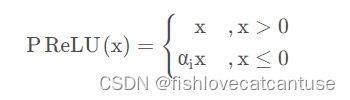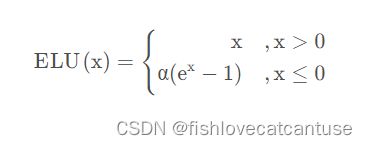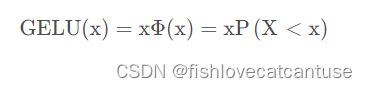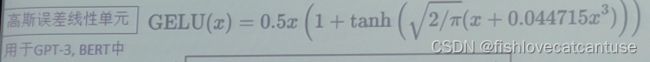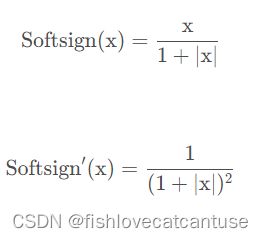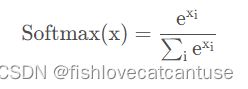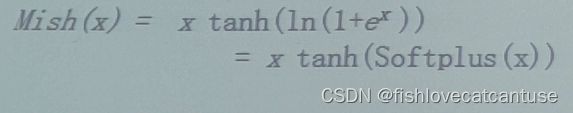Day4_深度学习常见的激活函数选择
本文很多都是来源互联网整理所得,源侵删。
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。因此可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。 那么激活函数应该具有什么样的性质呢?
可微性: 当优化方法是基于梯度的时候,这个性质是必须的。
单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数(导数在该区间上单调不减)。
输出值的范围: 当激活函数输出值是有限的时候,基于梯度的优化方法会更加稳定,因为特征的表示受有限权值的影响更显著;当激活函数的输出是无限的时候,模型的训练会更加高效,不过在这种情况小,一般需要更小的learning rate。
激活函数的作用是引入非线性因素。
在我们面对线性可分的数据集的时候,简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的,面对这样的数据,一般有两个方法:引入非线性函数、线性变换(把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。)。
饱和性问题:
Sigmoid(过去很常用,常用于二分类或多标签分类;隐层或者输出层;):
Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。在深度学习中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的激活函数,将变量映射到[0,1]之间。此外,(0, 1) 的输出还可以被表示作概率,或用于输入的归一化,代表性的如Sigmoid交叉熵损失函数。
图像:
公式:
特点:
- sigmoid也有其自身的缺陷,最明显的就是饱和性。从上图可以看到,其两侧导数逐渐趋近于0具有这种性质的称为软饱和激活函数。一旦输入落入饱和区,f′(x)f′(x) 就会变得接近于0,导致了向底层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。
- Sigmoid函数的导数是其本身的函数,即f′(x)=f(x)(1−f(x))f′(x)=f(x)(1−f(x))
- Sigmoid函数的输出范围是0到1。由于输出值限定在0到1,因此它对每个神经元的输出进行了归一化。
- 用于将预测概率作为输出的模型。由于概率的取值范围是0到1,因此Sigmoid函数非常合适分类模型。
- 梯度平滑,避免跳跃的输出值。
- 函数是可微的。这意味着可以找到任意两个点的Sigmoid曲线的斜率。
- 明确的预测,即非常接近1或0。
- sigmoid函数的输出均大于0,使得输出不是0均值,这称为偏移现象,这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。函数输出不是以0为中心的,这会降低权重更新的效率
- Sigmoid函数执行指数运算,计算机运行得较慢。
Tanh(双曲正切函数 ;Hyperbolic tangent function;隐层;循环神经网络):
双曲正切函数是双曲函数的一种。双曲正切函数在数学语言上一般写作tanh。它解决了Sigmoid函数的不以0为中心输出问题,然而,梯度消失的问题(饱和性)和幂运算(运行慢)的问题仍然存在。
图像:
公式:
特点:
- 将一个实值输入压缩至 [-1, 1]的范围,这类函数具有平滑和渐近性,并保持单调性。
- 相较于sigmoid函数,tanh关于0点对称。
- 执行指数运算,计算机运行得较慢。
ReLU系列激活函数(隐层)
ReLU是分段线性激活函数
SELU就是给ELU乘上系数![]()
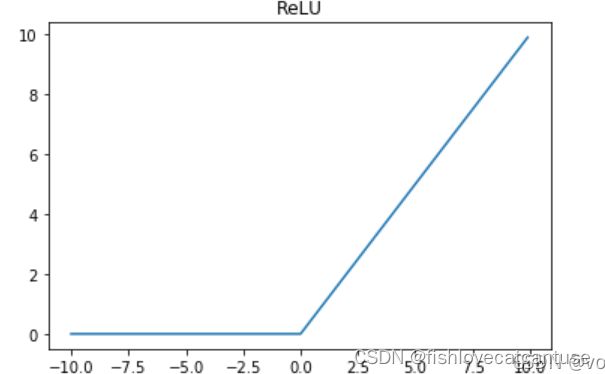
ReLU(目前最常用;Rectified linear unit; 修正线性单元 ):
线性整流函数,又称修正线性单元ReLU,是一种人工神经网络中常用的激活函数,通常指代以斜坡函数及其变种为代表的非线性函数。
图像:
公式:
特点:
- 使用梯度下降(GD)法时,收敛速度更快
- 只需要一个门限值,即可以得到激活值,计算速度更快
- 当输入为正时,不存在梯度饱和问题。
- 计算速度快得多。ReLU 函数中只存在线性关系,因此它的计算速度比Sigmoid函数和tanh函数更快。
- Dead ReLU:Relu的输入值为负的时候,输出始终为0,其一阶导数也始终为0,这样会导致神经元不能更新参数,也就是神经元不学习了,这种现象叫做“Dead Neuron”(Dead ReLU)。
- 函数不适应较大梯度输入,因为在参数更新以后,ReLU的神经元
不会再有激活的功能,导致梯度永远都是零。如果 learning rate 很大,那么很有可能网络中的 40% 的神经元都”dead”了。 - 在反向传播过程中,如果输入负数,则梯度将完全为零,Sigmoid函数和tanh函数也具有相同的问题。
- ReLU函数的输出为0或正数,这意味着ReLU函数不是以0为中心的函数。
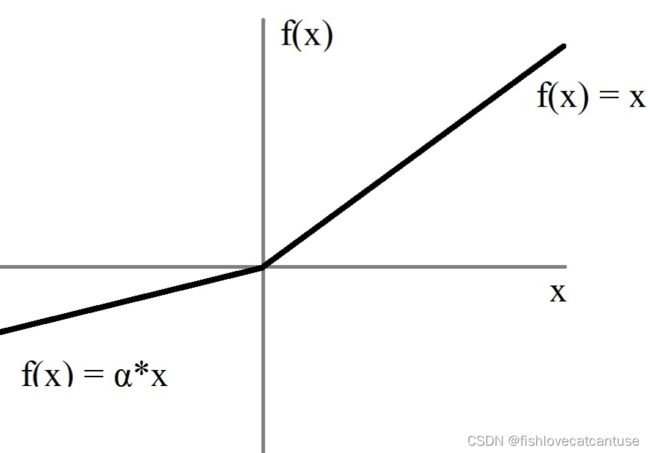
LReLU(Leaky Relu;带泄漏单元的relu):
它是一种专门设计用于解决Dead ReLU问题的激活函数
图像:
公式:
特点:
- Leaky ReLU函数通过把x的非常小的线性分量给予负输入0.01x来调整负值的零梯度问题。
- Leaky有助于扩大ReLU函数的范围,通常α的值为0.01左右。
- Leaky ReLU的函数范围是负无穷到正无穷。
PReLU(Parametric ReLU参数 ReLU):
ReLU 的改进版本。
图像:与LReLU大致一样
公式:
特点:
如果 αi是随机的参数,则PReLU(x)为RReLU函数。
- 在负值域,PReLU的斜率较小,这也可以避免Dead ReLU问题。
- 与ELU相比,PReLU 在负值域是线性运算。尽管斜率很小,但不会趋于0。
RReLU(随机ReLU):
LReLU的基础上,从均匀分布U(I,u)中随机抽取的一个数值![]() ,作为负值的斜率。
,作为负值的斜率。
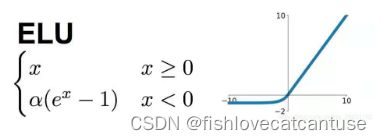
ELU(Exponential Linear Unit指数线性单位):
ELU 的提出也解决了ReLU 的问题。与ReLU相比,ELU有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度。
图像:
公式:
特点:
- 没有Dead ReLU问题,输出的平均值接近0,以0为中心。
- 作为非饱和激活函数,它不会遇到梯度爆炸或消失的问题。
- 与其他线性非饱和激活函数(如 ReLU 及其变体)相比,它有着更快的训练时间。
- ELU 通过减少偏置偏移的影响,使正常梯度更接近于单位自然梯度,从而使均值向零加速学习。
- ELU函数在较小的输入下会饱和至负值,从而减少前向传播的变化和信息。
- ELU与 ReLU 及其变体相比,由于负输入涉及非线性,因此计算速度较慢。 然而,在训练期间,ELU 的更快收敛足以弥补这一点。 但是在测试期间,ELU 的性能会比 ReLU 及其变体慢。
- 目前在实践中没有充分的证据表明ELU总是比ReLU好。
GELU(Gaussian error linear units,高斯误差线性单元;常用于深度自然语言理解,BERT,GPT-3):
Gelu在论文中已经被验证,是一种高性能的神经网络激活函数,因为GELU的非线性变化是一种符合预期的随机正则变换方式。
图像:
公式:
特点:
- GELU的神经网络优于使用ReLU作为激活的神经网络的实例。GELU也被用于BERT。
- 高斯误差线性单元正是在激活中引入了随机正则的思想,是一种对神经元输入的概率描述,直观上更符合自然的认识,同时实验效果要比ReLU与ELU都要好。
其他
Softplus(Logistic-Sigmoid函数原函数):
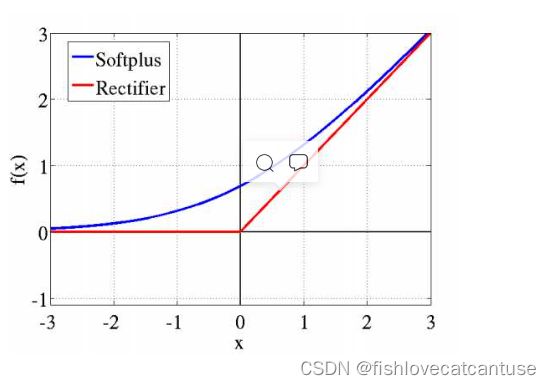
Softplus函数可以看作是ReLU函数的平滑。根据神经科学家的相关研究,Softplus函数和ReLU函数与脑神经元激活频率函数有神似的地方。也就是说,相比于早期的激活函数,Softplus函数和ReLU函数更加接近脑神经元的激活模型,而神经网络正是基于脑神经科学发展而来,这两个激活函数的应用促成了神经网络研究的新浪潮。 下图红色的即为ReLU。
图像:
公式:
![]()
特点:
- 输出恒为正。
- Softplus可以看作是ReLU平滑版本。
Softsign:
Softsign函数是Tanh函数的另一个替代选择。就像Tanh函数一样,Softsign函数是反对称、去中心、可微分,并返回-1和1之间的值。
图像:
公式:
特点:
- Softsign函数更平坦的曲线与更慢的下降导数表明它可以更高效地学习,比Tanh函数更好的解决梯度消失的问题。
- Softsign函数的导数的计算比Tanh函数更麻烦。
Maxout:
Maxout函数可以理解为是神经网络中的一层网络,类似于池化层、卷积层一样。可以把Maxout函数看成是网络的激活函数层,我们假设网络某一层的输入特征向量为:x = ( x 1 , x 2 , ⋯ , x d ),也就是我们输入是d个神经元。Maxout函数的输出如下:
图像:
如图可直观的看出
特点:
- maxout激活函数并不是一个固定的函数,不像Sigmod、Relu、Tanh等函数,是一个固定的函数方程
- 它是一个可学习的激活函数,因为我们W参数是学习变化的。
- 它是一个分段线性函数。
- maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。maxout是一个函数逼近器。
Softmax:
Softmax函数是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为K的任意实向量,Softmax函数可以将其压缩为长度为K,值在[0,1]范围内,并且向量中元素的总和为1的实向量。
公式:
特点:
- 在零点不可微。
- 用于多类分类问题的激活函数,Softmax函数的分母结合了原始输出值的所有因子,这意味着Softmax函数获得的各种概率彼此相关。
- 只用于输出层。
- 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
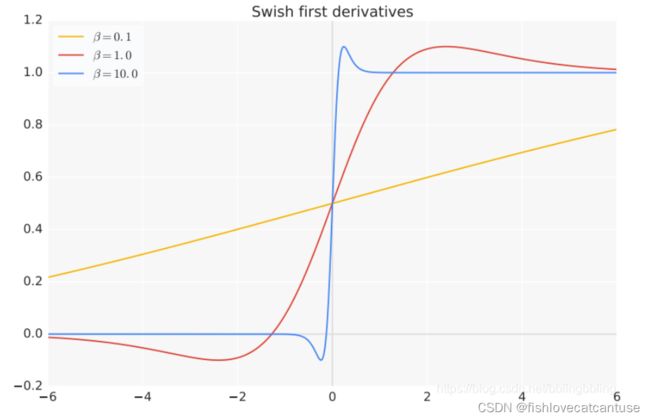
Swish(;隐层):
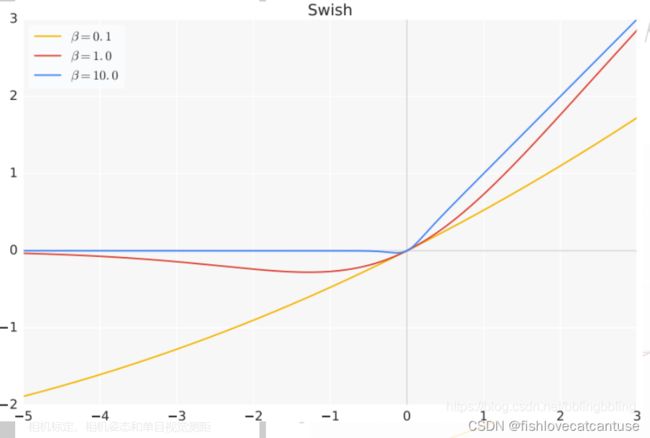
谷歌大脑团队提出了新型激活函数 Swish,团队实验表明使用 Swish 直接替换 ReLU 激活函数总体上可令 DNN 的测试准确度提升。此外,该激活函数的形式十分简单,且提供了平滑、非单调等特性从而提升了整个神经网络的性能。
图像:
公式:
特点:
- 当β = 0时,Swish激活函数变为线性函数 f(x) = x/2.
- 当β = ∞ 时,Swish激活函数变为0或x,相当于Relu,
- 所以,Swish函数可以看作是介于线性函数与ReLU函数之间的平滑函数。
- Swish函数和其一阶导数都具有平滑特性;
- 有下界,无上界,非单调。
Mish(;隐层)
Diganta Misra的一篇题为“Mish: A Self Regularized Non-Monotonic Neural Activation Function”的新论文介绍了一个新的深度学习激活函数,该函数在最终准确度上比Swish(+.494%)和ReLU(+ 1.671%)都有提高。
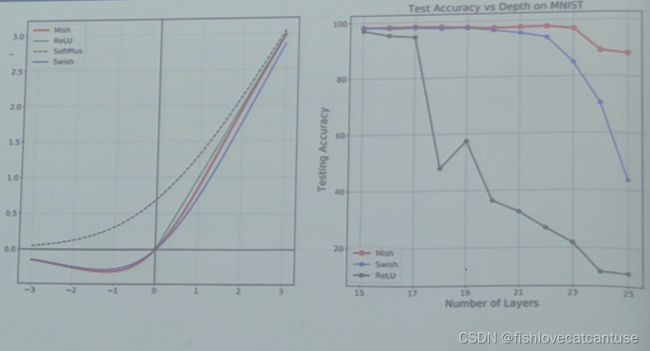
图像:
公式:
特点:
- Mish,Swish,ReLU的曲线非常相似,x<0时,Mish在最下; x>0时,Mish位于ReLU和Swish之间。
- Mi sh和Swish的性能超过了ReLU和Leaky ReLU,但从计算复杂度/硬件实现的角度,ReLU最佳, Mish计算太费资源。
- 以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流,而不是像ReLU中那样的硬零边界。最后,可能也是最重要的,目前的想法是,平滑的激活函数允许更好的信息深入神经网络,从而得到更好的准确性和泛化。