Python图像处理笔记——傅里叶变换

---

一、前言

图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。（灰度变化得快频率就高，灰度变化得慢频率就低）。傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。
傅立叶变换的物理意义：
将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

傅立叶变换以前，图像（未压缩的位图）是由对在连续空间（现实空间）上的采样得到一系列点的集合，我们习惯用一个二维矩阵表示空间上各点，则图像可由z=f(x,y)来表示。由于空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就由梯度来表示，这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度？因为实际上对图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也是没有。

关于傅里叶变换的详细解读推荐阅读大佬的知乎专栏：链接

---

二、傅里叶变换在图像中的应用

空域的卷积相当于频域的乘法。

在空间域，图像与高斯核卷积可以实现高斯模糊的效果。相当于，高斯核和图像在频域的乘积。

0. 本文用到的库

import timeit
import matplotlib.pylab as plt
import numpy as np
import pylab
from skimage.io import imread
from scipy import signal
import scipy.fftpack as fp
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter

1. 图像的傅里叶变换和逆变换

将图像转换到频域，然后逆变换重建图像，信噪比不变。基于scipy.fftpack的傅里叶变换函数实现。

def calc_snr(img, axis=0, ddof=0): # 计算信噪比
    a = np.asanyarray(img)
    m = a.mean(axis)
    sd = a.std(axis=axis, ddof=ddof)
    return np.where(sd == 0, 0, m / sd)

im = np.array(Image.open('images.jpg').convert('L'))
snr = calc_snr(img, axis=None)
print('SNR for the original image is ' + str(snr))
freq = fp.fft2(img)
im1 = fp.ifft2(freq).real  # 取实部重建图像
freq2 = fp.fftshift(freq)  # 移位变换系数，使得直流分量在中间
img_mag = 20 * np.log10(0.1 + np.abs(freq2))
img_phase = np.angle(freq2)
snr = calc_snr(im1, axis=None)
print('SNR for the image obtained after fft reconstruction is ' + str(snr))
# Make sure the forward and backward transforms work!
assert(np.allclose(im, im1))

输出

SNR for the original image is 3.3597120699464553
SNR for the image obtained after fft reconstruction is 3.3597120699464553

2. 高斯模糊

在空域中，图像与高斯核卷积可以实现高斯模糊。利于傅里叶变换的方法可以大幅减少计算量。以下是Python代码：

im = np.mean(imread('image.jpg'), axis=2)
gauss_kernel = np.outer(signal.gaussian(im.shape[0], 2), signal.gaussian(im.shape[1], 2))
freq = fp.fft2(im) # 原图像的傅里叶变换
assert (freq.shape == gauss_kernel.shape) # 检查大小是否相等
freq_kernel = fp.fft2(fp.fftshift(gauss_kernel)) # 高斯核的傅里叶变换
freq_convolved = freq_kernel * freq # 频域相乘，即空域卷积结果
im1 = fp.ifft2(freq_convolved).real # 逆傅里叶变换
# 调整频域图
freq = 20 * np.log10(0.1 + fp.fftshift(freq)).astype(int)
freq_kernel = 20 * np.log10(0.1 + fp.fftshift(freq_kernel)).astype(int)
freq_convolved = 20 * np.log10(0.1 + fp.fftshift(freq_convolved)).astype(int)

示例

3. 傅里叶变换频域滤波

不同的频率分量对应图像中的不同部分。简单来说，低频对应细节，高频对应边缘。

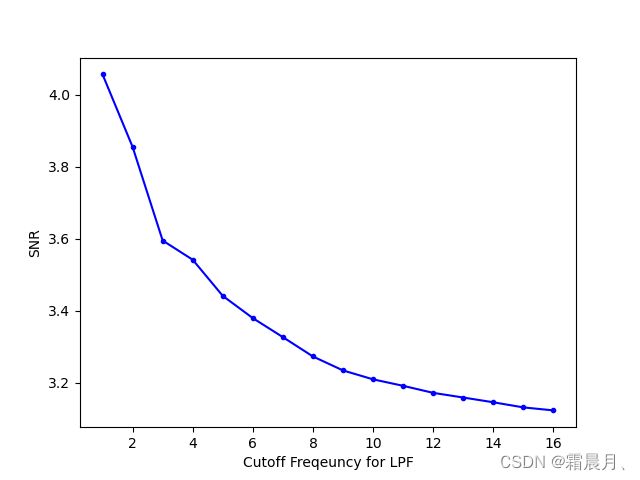
（1）低通滤波

im = np.array(Image.open('../images/rhino.jpg').convert('L')) #
freq = fp.fft2(im)
(w, h) = freq.shape
half_w, half_h = int(w/2), int(h/2)

snrs_lp = []
ubs = list(range(1,17))
plt.figure(figsize=(10,10))
for u in ubs:
    freq1 = np.copy(freq)
    freq2 = fp.fftshift(freq1)
    freq2_low = np.copy(freq2)
    freq2_low[half_w-u:half_w+u+1,half_h-u:half_h+u+1] = 0
    freq2 -= freq2_low 
    im1 = np.clip(fp.ifft2(fp.ifftshift(freq2)).real,0,255)
    snrs_lp.append(calc_snr(im1, axis=None))

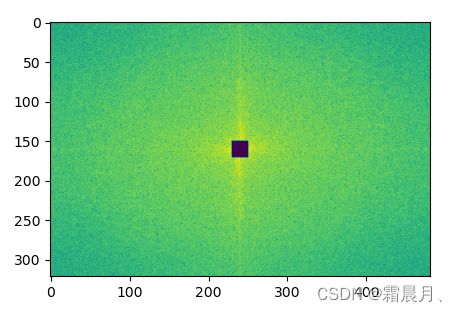
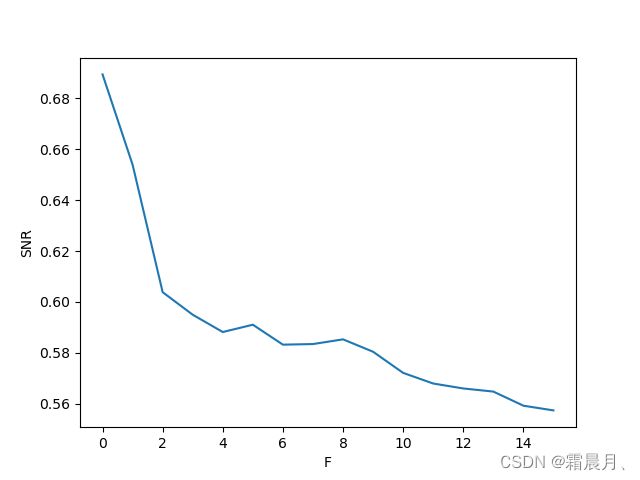
（2）高通滤波

snrs_hp = []
# snrs_hp.append(calc_snr(im, axis=None)) # 原图的SNR
lbs = list(range(1,17,1)) # 截止频率
for l in lbs:
    freq1 = np.copy(freq)
    freq2 = fp.fftshift(freq1)
    # high pass
    freq2[half_w-l:half_w+l+1,half_h-l:half_h+l+1] = 0 
    # 逆变换
    im1 = np.clip(fp.ifft2(fp.ifftshift(freq2)).real,0,255) 
    # 计算SNR
    snrs_hp.append(calc_snr(im1, axis=None))

以下是运行结果，可以看到截止频率对滤波效果的影响。

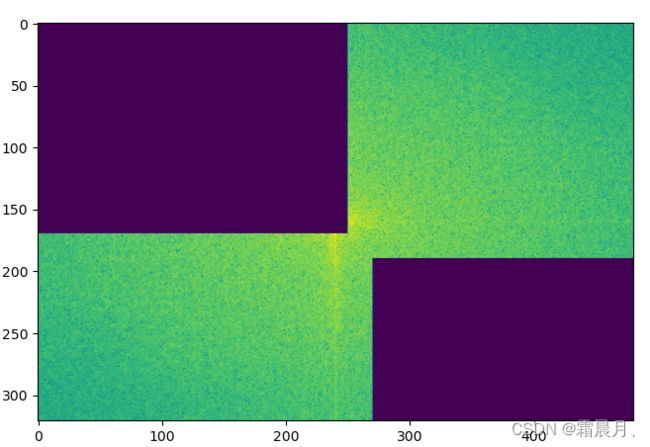
（3）带通滤波

freq1 = np.copy(freq)
freq2 = fp.fftshift(freq1)
freq2[:half_w+10,:half_h+10] = freq2[half_w+30:,half_h+30:] = 0 
im1 = np.clip(fp.ifft2(fp.ifftshift(freq2)).real,0,255)