英飞凌TC264无刷驱动方案simplefoc移植(4)-SimpleFOC矢量控制实现
英飞凌TC264无刷驱动方案simplefoc移植(4)-SimpleFOC矢量控制实现
上一篇文章主要讲解了,矢量控制的原理,变换以及逆变换,电流采样,闭环pid,以及svpwm换向。但是这些在simple中又是如何实现的呢
- 英飞凌TC264无刷驱动方案simplefoc移植(4)-SimpleFOC矢量控制实现
- 一、闭环方案
- 二、转矩控制
- 三、ua,ub ,uc三相电压计算
-
- 3-1 正弦调制SinePWM
- 3-2 空间矢量调制 SpaceVectorPWM
- 四、逆变方案选择
- 五、PID控制
- 六、低通速度滤波器
本文主要参考
SimpleFOClibrary-github
Arduino Simple Field Oriented Control (FOC) 项目 - 中文官网
一、闭环方案
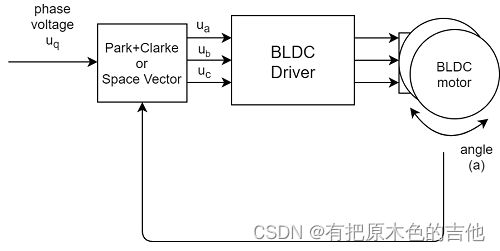
与传统的矢量控制相比,simplefoc省了电流采样,chark变换和park变换,取而代之的是直接反馈角度,利用(正弦调制SinePWM或者是空间矢量调制 SpaceVectorPWM)控制无刷电机,
这也恰好是simplefoc的魅力,省去了很多结构,而且算法也比较简单,当热也带来了一些缺陷,速度无法向商业电调相比。
二、转矩控制
电压控制算法从位置传感器读取角度a,从用户获取目标Uq电压值,通过FOC算法设置电机合适的U a, U b 和 U c。FOC算法确保这些电压在电机转子中产生的磁力与其永磁体的90度偏移,这保证了最大扭矩,这称为换相。
对于精确实现直流电机原理来说这是一种困难的方法。因为对于直流电动机来说,转子所产生的磁场与定子所产生的永磁场之间的90度角是基于硬件实现的。现在,当你有FOC算法保证的90度约束,你可以使用这个电压控制方法去控制任何其他直流电机。
对于直流电动机,我们知道电机扭矩 T与电流I成正比:
T = I ∗ K T = I*K T=I∗K
其中 K 是由其硬件定义的电机常数。 我们还知道,电流与设定的电压U成正比:
I = ( U − E M F ) / R I = (U - EMF)/R I=(U−EMF)/R
其中 R是电机内阻,EMF是产生的反EMF电压。这个方程没有考虑任何动力学因素,但总的来说还是很有效的。
所以我们可以从所有这些中得出的结论是(如果我们忽略EMF):
T ⊂ I ⊂ U T \subset I \subset U T⊂I⊂U
这意味着扭矩与电流成比例。而由于电流与电压成比例,那么扭矩也与电压成比例。
另一种理解为什么我们需要在转子和定子磁场之间形成90度角的方法是记住导线穿过磁场时产生的电场的方程:
F = B ∗ I ∗ L ∗ s i n ( a l p h a ) F = B*I*L*sin(alpha) F=B∗I∗L∗sin(alpha)
其中B 是磁场的强度, L是导电流的大小, alpha是磁场B和电流, I之间的角度。从这个方程中我们可以看到,为了获得最大的力 F = BIL ,我们需要保持alpha角等于90度或 PI/2弧度。
三、ua,ub ,uc三相电压计算
在simplefoc中实现 有两种方案,下边将分别讲解二者的不同
正弦PWM: SinePWM
空间矢量PWM: SpaceVectorPWM
可以通过设置 motor.foc_modulation 的变量值进行配置:
motor.foc_modulation = FOCModulationType::SinePWM; // default
// or
motor.foc_modulation = FOCModulationType::SpaceVectorPWM;
3-1 正弦调制SinePWM
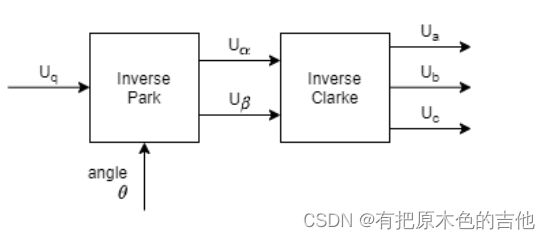
逆Park变换法:
{ U α = − U q s i n ( θ ) U β = − U q c o s ( θ ) \begin{cases} U~\alpha~ = -U~q~sin(\theta) \\ U~\beta~ = -U~q~cos(\theta) \end{cases} {U α =−U q sin(θ)U β =−U q cos(θ)
逆Clark变换法:
{ U a = U α U b = ( − U α + ( 3 ) U β ) / 2 U c = ( − U α − ( 3 ) U β ) / 2 \begin{cases} U~a~ = U~\alpha~ \\ U~b~ = (-U~\alpha~ + \sqrt(3)U~\beta~)/2\\ U~c~ = (-U~\alpha~ - \sqrt(3)U~\beta~)/2 \end{cases} ⎩ ⎨ ⎧U a =U α U b =(−U α +(3)U β )/2U c =(−U α −(3)U β )/2
以下是在中实现正弦PWM的代码:
// 使用FOC将Uq设置到电机的最佳角度
void BLDCMotor::setPhaseVoltage(float Uq, float angle_el) {
// 正弦PWM调制
// 逆派克+克拉克变换
// 角度在0和360°之间的归一化
// 仅当使用_sin和_cos近似函数时才需要
angle_el = normalizeAngle(angle_el + zero_electric_angle);
// 逆派克变换
Ualpha = -_sin(angle_el) * Uq; // -sin(angle) * Uq;
Ubeta = _cos(angle_el) * Uq; // cos(angle) * Uq;
// 你克拉克变换
Ua = Ualpha + voltage_power_supply/2;
Ub = -0.5 * Ualpha + _SQRT3_2 * Ubeta + voltage_power_supply/2;
Uc = -0.5 * Ualpha - _SQRT3_2 * Ubeta + voltage_power_supply/2;
// 给硬件设定电压
setPwm(Ua, Ub, Uc);
}
3-2 空间矢量调制 SpaceVectorPWM
空间矢量调制基于两个步骤的计算:

在第一步,我们发现扇区s转子目前在。360度的角被分成6等份的60度。这个计算很简单。然后我们计算时间T0, T1 和 T2。T1 和 T2告诉我们第一阶段和第二阶段应该开多久,T0告诉我们电机上0电压应该开多久。
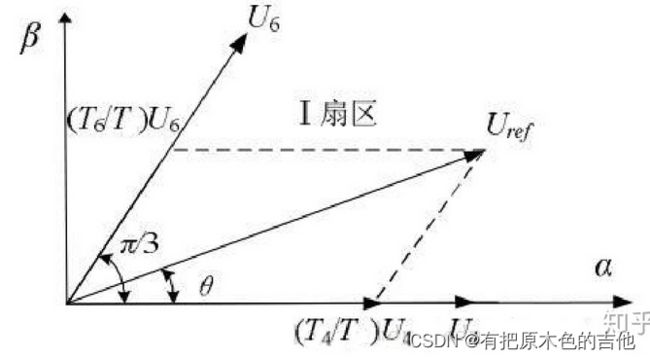
{ s = ⌊ 3 θ π ⌋ + 1 T 1 = ( 3 ) s i n ( s π 3 − θ ) T 2 = ( 3 ) s i n ( θ − ( s − 1 ) π 3 ) T 0 = 1 − T 1 − T 2 \begin{cases} s = \lfloor \frac{3\theta}{\pi}\rfloor + 1 \\ T~1~ = \sqrt(3) sin(s \frac{\pi}{3} - \theta)\\ T~2~ = \sqrt(3) sin(\theta- (s-1) \frac{\pi}{3} )\\ T~0~ = 1 - T~1~ - T~2~ \end{cases} ⎩ ⎨ ⎧s=⌊π3θ⌋+1T 1 =(3)sin(s3π−θ)T 2 =(3)sin(θ−(s−1)3π)T 0 =1−T 1 −T 2
第二步是将T0,1,2值投影到适当的占空比Ta,b,c,这些占空比直接取决于电机当前所在的扇区。
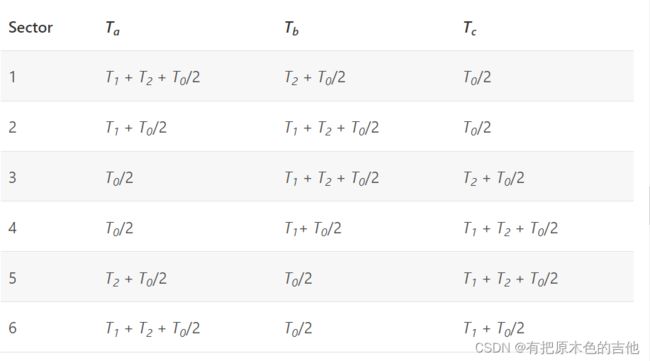
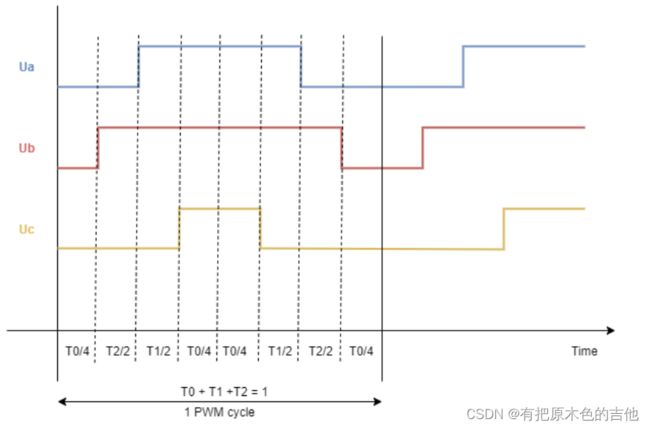
下面是一个例子使用SVM表生成pwm信号的参数: s = 2, T1 = 1/8 = 0.125, T2 = 1/8 = 0.125 and T0 = 1/2 = 0.5
 这里是空间矢量PWM实现的代码在 SimpleFOClibrary :
这里是空间矢量PWM实现的代码在 SimpleFOClibrary :
// 使用FOC将Uq设置到电机的最佳角度
void BLDCMotor::setPhaseVoltage(float Uq, float angle_el) {
// 解释SpaceVectorModulation (SVPWM)算法的视频如下
// https://www.youtube.com/watch?v=QMSWUMEAejg
// 如果负电压的变化与相相反
// 角度 +180°
if(Uq < 0) angle_el += _PI;
Uq = abs(Uq);
// 角度归一化,在0和360°之间
// 仅当使用_sin和_cos近似函数时才需要
angle_el = normalizeAngle(angle_el + zero_electric_angle + _PI_2);
// 找到我们目前所在的象限
int sector = floor(angle_el / _PI_3) + 1;
// 计算占空比
float T1 = _SQRT3*_sin(sector*_PI_3 - angle_el) * Uq/voltage_power_supply;
float T2 = _SQRT3*_sin(angle_el - (sector-1.0)*_PI_3) * Uq/voltage_power_supply;
// 两个版本
// 以电压电源为中心/2
float T0 = 1 - T1 - T2;
// 低电源电压,拉到0
//float T0 = 0;
// 计算占空比(时间)
float Ta,Tb,Tc;
switch(sector){
case 1:
Ta = T1 + T2 + T0/2;
Tb = T2 + T0/2;
Tc = T0/2;
break;
case 2:
Ta = T1 + T0/2;
Tb = T1 + T2 + T0/2;
Tc = T0/2;
break;
case 3:
Ta = T0/2;
Tb = T1 + T2 + T0/2;
Tc = T2 + T0/2;
break;
case 4:
Ta = T0/2;
Tb = T1+ T0/2;
Tc = T1 + T2 + T0/2;
break;
case 5:
Ta = T2 + T0/2;
Tb = T0/2;
Tc = T1 + T2 + T0/2;
break;
case 6:
Ta = T1 + T2 + T0/2;
Tb = T0/2;
Tc = T1 + T0/2;
break;
default:
// 可能的错误状态
Ta = 0;
Tb = 0;
Tc = 0;
}
// 计算相电压和中心
Ua = Ta*voltage_power_supply;
Ub = Tb*voltage_power_supply;
Uc = Tc*voltage_power_supply;
break;
}
// 设置硬件中的电压
setPwm(Ua, Ub, Uc);
}
四、逆变方案选择
这是由 Uq = 0.5V的正弦和空间矢量调制产生的波形图像:
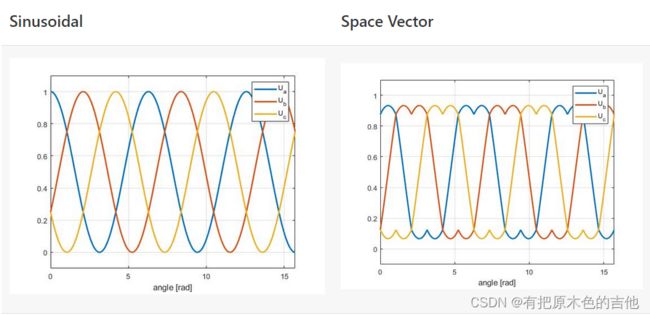
两种算法之间有几个关键的区别。但就SimpleFOClibrary而言,你需要知道的就是空间矢量算法更好地使用了电源的最大电压范围。在上面的表格中,你可以看到,对于Uq = 0.5V,正弦调制产生的正弦波的幅度正好等于1,空间矢量调制还不是平静的。由空间矢量产生的“双正弦波”的幅值为 2/sqrt(3) = 1.15 ,这意味着在使用相同的电源时,它可以向电机多输出15%的功率。
这意味着,当使用SinePWM时,你的供电电压 Vpower_supply可以设置最大为 Uq = 0.5 Vpower_supply 。如果使用 SpaceVectorPWM,你将能够设置Uq = 0.58 Vpower_supply
你应该通过改变电机参数motor.voltage_power_supply的值来指定电源电压Vpower_supply。默认值为 12V。如果你需要设置你的Vpower_supply为其他值,在这里更改它,FOC算法将据此调整适当的Uq (motor.voltage_q)值。
// 电源电压
motor.voltage_power_supply = 12;
如果你试着把电压 Uq高于Uq = 0.5 Vpower_supply 给 SinePWM或 Uq = 0.58 Vpower_supply给SpaceVectorPWM,它仍然会工作,但 Ua,b,c信号会饱和。
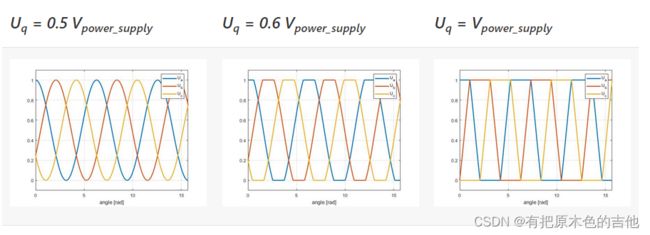
这里有一些 SinePWM的不同Uq值的图像。
基本上你可以在图像上看到的是Ua,b,c是饱和的,在你超过最大值后,你实际上不再设置正弦波到你的电机。 电机的功率仍在增加,但不再是直线或平滑的。
五、PID控制
PID算法在 PIDController 中的SimpleFOClibrary中实现
// PID控制器的功能
float PIDController::operator() (float error){
// 计算最新调用的时间
unsigned long timestamp_now = _micros();
float Ts = (timestamp_now - timestamp_prev) * 1e-6;
// 快速修复错误的情况 (micros overflow)
if(Ts <= 0 || Ts > 0.5) Ts = 1e-3;
// u(s) = (P + I/s + Ds)e(s)
// 实现离散
// 成比例的部分
// u_p = P *e(k)
float proportional = P * error;
// 积分部分的Tustin变换
// u_ik = u_ik_1 + I*Ts/2*(ek + ek_1)
float integral = integral_prev + I*Ts*0.5*(error + error_prev);
// 限制输出电压q
integral = _constrain(integral, -limit, limit);
// 离散的推导
// u_dk = D(ek - ek_1)/Ts
float derivative = D*(error - error_prev)/Ts;
// 求和所有的分量
float output = proportional + integral + derivative;
// 限制输出变量
output = _constrain(output, -limit, limit);
// 通过提高输出来限制加速度
float output_rate = (output - output_prev)/Ts;
if (output_rate > output_ramp)
output = output_prev + output_ramp*Ts;
else if (output_rate < -output_ramp)
output = output_prev - output_ramp*Ts;
// 为下一浏览存储
integral_prev = integral;
output_prev = output;
error_prev = error;
timestamp_prev = timestamp_now;
return output;
}
这个PID是在BLDCMotor和 StepperMotor中实现的,用于处理运动控制速度(motor.PID_velocity)和位置 (motor.P_angle)。你可以通过更改这些PID控制器的公共变量来更改它们的参数
六、低通速度滤波器
控制器的低通滤波器传递函数为
G f = 1 1 + S T f G~f~ = \frac{1}{1 + ST~f~} G f =1+ST f 1
离散化为:
V f ( k ) = T f T f + T s ∗ V f ( k − 1 ) + T f T f + T s ∗ V ( k ) V~f~(k) = \frac{T~f~}{T~f~ + T~s~}*V~f~(k-1) + \frac{T~f~}{T~f~ + T~s~}*V(k) V f (k)=T f +T s T f ∗V f (k−1)+T f +T s T f ∗V(k)
中vf(k)为k时刻的滤波值, v(k)为k时刻的速度测量值, Tf是滤波时间常数,Ts是采样时间(或上述式子的时间间隔)。 这个低通滤波器也可以写成这样的形式:
V f ( k ) = α ∗ V f ( k − 1 ) + α ∗ V ( k ) V~f~(k) = \alpha *V~f~(k-1) + \alpha *V(k) V f (k)=α∗V f (k−1)+α∗V(k)
α = T f T f + T s \alpha = \frac{T~f~}{T~f~ + T~s~} α=T f +T s T f
设置 T_f = 0.01 将得到:
alpha = 0.01/(0.01 + 0.001) = 0.91
上式表示实际的速度测量值v会通过系数1-alpha = 0.09影响到滤波后的值vf,从而令速度的变化更加平滑(平滑程序取决于实际应用)。
滤波的实现如下:
// 低通滤波函数
float LowPassFilter::operator(float input){
unsigned long timestamp = _micros();
float dt = (timestamp - timestamp_prev)*1e-6f;
// 快速修复错误的情况 (micros overflow)
if (dt < 0.0f || dt > 0.5f) dt = 1e-3f;
// 计算过滤
float alpha = Tf/(Tf + dt);
float y = alpha*y_prev + (1.0f - alpha)*x;
// 保存的变量
y_prev = y;
timestamp_prev = timestamp;
return y;
}
调用的时候直接调用就可以了
float signal_filtered = filter(signal);