视觉机器学习20讲-MATLAB源码示例（7）-EM算法

1. EM算法

最大期望算法（Expectation-Maximization algorithm, EM），或Dempster-Laird-Rubin算法 ，是一类通过迭代进行极大似然估计（Maximum Likelihood Estimation, MLE）的优化算法 ，通常作为牛顿迭代法（Newton-Raphson method）的替代用于对包含隐变量（latent variable）或缺失数据（incomplete-data）的概率模型进行参数估计。
　
EM算法是一个基础算法，是很多机器学习领域算法的基础，比如隐式马尔科夫算法（HMM）， LDA主题模型的变分推断等等。

2. Matlab仿真

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能：演示EM算法在计算机视觉中的应用
%基于EM算法实现目标分类；
%环境：Win7，Matlab2018a
%Modi: C.S
%时间：2022-4-5
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

mu1=[0 6];
mu2=[0 0];
mu3=[6,-6];
sigma1=[8 0; 0 1]
r1=mvnrnd(mu1,sigma1,100);
r2=mvnrnd(mu2,sigma1,100);
r3=mvnrnd(mu3,sigma1,100)
data(1:100,:)=r1;
data(101:200,:)=r2;
data(201:300,:)=r3;
[n,d]=size(data)
M=3;
sigma=zeros(d,d,M);
Mu=zeros(M,d);
size(Mu)
priors=zeros(1,M);
[priors, Mu,sigma] = EM_init_kmeans(data', M)

max_iter=20;
for i=1:max_iter
    p=zeros(M,n);%%p=p(x|j)
    E=zeros(M,n);
    %% E-step
    for j=1:M
       if det(sigma(:,:,j))==0
           sigma(:,:,j)=ones*exp(-100);%保证矩阵可逆
           
       end
       detS=det(sigma(:,:,j));
       invS=inv(sigma(:,:,j));
       for k=1:n         
           p(j,k)=(2*pi)^(-d/2)*(detS)^(-1/2)*exp(-1/2*(data(k,:)-Mu(j,:))*invS*(data(k,:)-Mu(j,:))');
           E(j,k)=p(j,k)*priors(j);        
       end
    end
    E=E./(ones(M,1)*sum(E));
    %% M-step
    w=zeros(1,M);
    Mu2=zeros(M,d);
    sigma2=zeros(d,d,M);
    % update mean 
    for k=1:M
        for j=1:n
            w(k)=w(k)+E(k,j);
            Mu2(k,:)=Mu2(k,:)+E(k,j)*data(j,:);       
        end
        Mu2(k,:)=Mu2(k,:)./w(k);
    end
    % update covariance
    for k=1:M
        for j=1:n
            dist=(Mu2(k,:)-data(j,:))*(Mu2(k,:)-data(j,:))';
            sigma2(:,:,k)=sigma2(:,:,k)+E(k,j)*dist;            
        end
        sigma2(:,:,k)=sigma2(:,:,k)./w(k);
        sigma2(:,:,k)=diag(diag(sigma2(:,:,k)));
        
    end
    %update prior probability
    priors=w./n;
    Mu=Mu2;
    sigma=sigma2;
    
end
%% data classification
[x,y]=meshgrid(-10:.1:10,-10:.1:10);
figure(2)
subplot(1,2,1)
plot(r1(:,1),r1(:,2),'*')
hold on
plot(r2(:,1),r2(:,2),'o')
hold on
plot(r3(:,1),r3(:,2),'+')
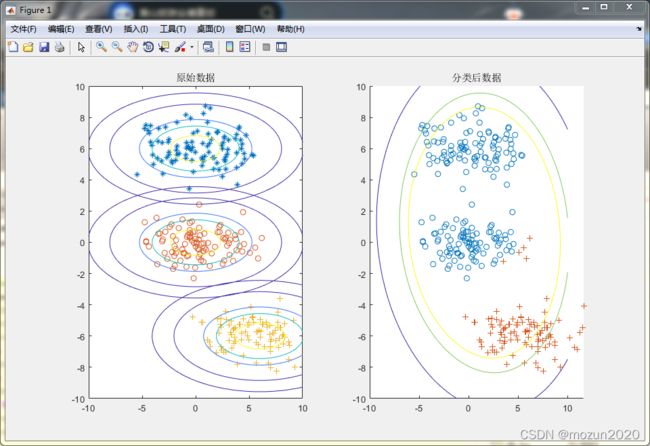
title('原始数据');
xlim([-10 10])
ylim([-10 10])

z1=mvnpdf([x(:) y(:)],mu1,sigma1);
z=zeros(size(z1));
z1 = reshape(z1,length(x),length(y));
hold on
contour(x,y,z1,[0.11 0.1 0.08 0.06 0.04 0.02 0.01 0.001 0.0001]);
z2=mvnpdf([x(:) y(:)],mu2,sigma1);
z2 = reshape(z2,length(x),length(y));
hold on
contour(x,y,z2,[0.11 0.1 0.08 0.06 0.04 0.02 0.01 0.001 0.0001]);
z3=mvnpdf([x(:) y(:)],mu3,sigma1);
z3 = reshape(z3,length(x),length(y));
hold on
contour(x,y,z3,[0.11 0.1 0.08 0.06 0.04 0.02 0.01 0.001 0.0001]);
subplot(1,2,2)

C=['*','O','+'];

maxE=max(E);
result=zeros(n,d,M);
%z=zeros(size(x,1)*size(y,1),1);
for i=1:M
    in=(E(i,:)==maxE);
    acount=find(E(i,:)==maxE);
    number=size(acount,2)
    if ~isempty(acount)
    result=zeros(size(acount,2),d);
    m=1
    x=acount(m);
    %m=1;
    for j=1:n
        if j==x;
            
            result(m,:)=data(x,:);
            m=m+1;
            if m>size(acount,2)
              break;  
            end
            x=acount(m);
            
            
        end
    end
  plot(result(:,1),result(:,2),C(i));
    end
  %x=diag(sigma(:,:,i))
  [x,y]=meshgrid(-10:.1:10,-10:.1:10);

   z=z+mvnpdf([x(:) y(:)],Mu(i,:),sigma(:,:,i))/priors(i);
  hold on
  
end
z = reshape(z,length(x),length(y));
contour(x,y,z,[0.025 0.02 0.01]);
title('分类后数据')

function [Priors, Mu, Sigma] = EM_init_kmeans(Data, nbStates)
[nbVar, nbData] = size(Data);
[Data_id, Centers] = kmeans(Data', nbStates); 
Mu = Centers;
for i=1:nbStates
  idtmp = find(Data_id==i);
  Priors(i) = length(idtmp);
  Sigma(:,:,i) = cov([Data(:,idtmp) Data(:,idtmp)]');
  %Add a tiny variance to avoid numerical instability
  Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
  Sigma(:,:,i)=diag(diag(Sigma(:,:,i)));
end
Priors = Priors ./ sum(Priors);

3. 仿真结果

4. 小结

从算法思想的角度来思考EM算法，可以发现算法里已知的是观察数据，未知的是隐含数据和模型参数，在E步，所做的事情是固定模型参数的值，优化隐含数据的分布，而在M步，所做的事情是固定隐含数据分布，优化模型参数的值。

比较下其他的机器学习算法，其实很多算法都有类似的思想。比如SMO算法（支持向量机原理(四)SMO算法原理），坐标轴下降法(Lasso回归算法： 坐标轴下降法与最小角回归法), 都使用了类似的思想来求解问题。

EM算法机器学习中很多算法都有应用，不论是监督学习还是无监督学习，有兴趣的推荐去仔细查看全文《机器学习20讲》中第七讲内容。

本系列文章列表如下：
视觉机器学习20讲-MATLAB源码示例（1）-Kmeans聚类算法
视觉机器学习20讲-MATLAB源码示例（2）-KNN学习算法
视觉机器学习20讲-MATLAB源码示例（3）-回归学习算法
视觉机器学习20讲-MATLAB源码示例（4）-决策树学习算法
视觉机器学习20讲-MATLAB源码示例（5）-随机森林（Random Forest）学习算法
视觉机器学习20讲-MATLAB源码示例（6）-贝叶斯学习算法
视觉机器学习20讲-MATLAB源码示例（7）-EM算法
视觉机器学习20讲-MATLAB源码示例（8）-Adaboost算法
视觉机器学习20讲-MATLAB源码示例（9）-SVM算法
视觉机器学习20讲-MATLAB源码示例（10）-增强学习算法
视觉机器学习20讲-MATLAB源码示例（11）-流形学习算法
视觉机器学习20讲-MATLAB源码示例（12）-RBF学习算法
视觉机器学习20讲-MATLAB源码示例（13）-稀疏表示算法
视觉机器学习20讲-MATLAB源码示例（14）-字典学习算法
视觉机器学习20讲-MATLAB源码示例（15）-BP学习算法
视觉机器学习20讲-MATLAB源码示例（16）-CNN学习算法
视觉机器学习20讲-MATLAB源码示例（17）-RBM学习算法
视觉机器学习20讲-MATLAB源码示例（18）-深度学习算法
视觉机器学习20讲-MATLAB源码示例（19）-遗传算法
视觉机器学习20讲-MATLAB源码示例（20）-蚁群算法