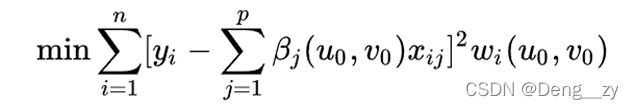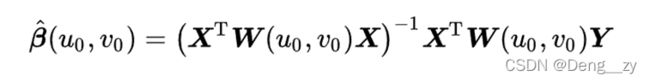GIS应用实例--模型预测、多元回归、空间自相关分析

免费数据和原报告详见个人主页

中国地质大学（武汉）地理信息系统原理课程报告_项目（免费）-行业报告文档类资源-CSDN文库https://download.csdn.net/download/qq_58010729/85076121
所有数据均来源于国家统计局等其他公开网站，仅供研究使用。

 目录

一、研究方法

1.1移动平滑法

1.2多元回归分析

1.3最小二乘法回归

1.4 地理加权回归分析

1.5 Moran指数分析

二、数据处理

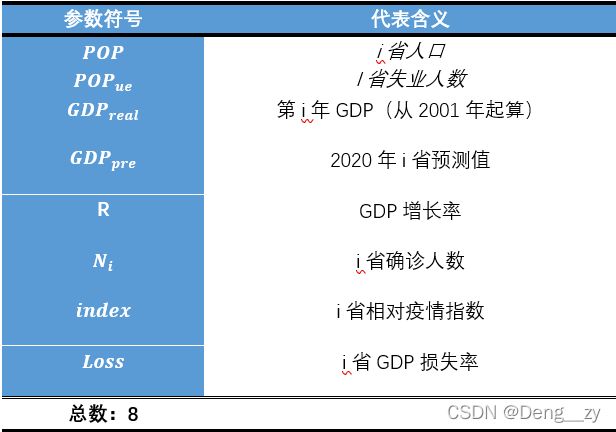
2.1 数据参数设计

2.2 空间自相关

2.3 疫情及其经济损失的影响因素分析（OLS+GWR）

2.4 疫情及其对各省经济发展的总体影响

三、结论

---

一、研究方法

1.1移动平滑法

移动平均法是根据时间序列资料逐渐推移，依次计算包含一定项数的时序平均数， 以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响，起伏较大，不易显示出发展趋势时，可用移动平均法，消除这些因素的影响，分析、预测序列的长期趋势。移动平均法有简单移动平均法，加权移动平均法，趋势移动平均法等。

简单移动平均法的简述：设有观测序列y1,y2,y3,⋯,yT,取移动平均的项数N<T。一次简单移动平均值计算公式为：

当预测目标的基本趋势是在某一水平上下波动时，可用一次简单移动平均方法建立预测模型：

其预测标准误差为：

                                                  

近N期序列值的平均值作为未来各期的预测结果。一般 N 的取值范围：5≤N ≤200。当历史序列的基本趋势变化不大且序列中随机变动成分较多时，N的取值应较大一些。否则N的取值应小一些。在有确定的季节变动周期的资料中，移动平均的项数应取周期长度。选择佳 N 值的一个有效方法是，比较若干模型的预测误差。预测标准误差小者为好。

简单移动平均法只适合做近期预测，而且是预测目标的发展趋势变化不大的情况。如果目标的发展趋势存在其它的变化，采用简单移动平均法就会产生较大的预测偏差和滞后。即当时间序列出现直线增加或减少的变动趋势时，用简单移动平均法来预测就会有滞后偏差。因此，需要进行修正，修正的方法就是作二次移动平均，利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。

                

在一次移动平均的基础上再进行一次移动平均就是二次移动平均，其计算公式为：

设时间序列{yt}从某时期开始具有直线趋势，且认为未来时期也按此直线趋势变化，则可设此直线趋势预测模型为:

                                          

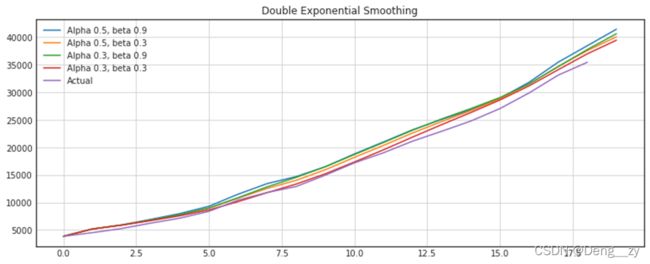
其中，t为当前时期数；T为由t至预测期的时期数；at为截距；bt为斜率。两者又称为平滑系数。但在后面实践中发现，从各年的预测来看，效果不太行，所以后来考虑了双指数平滑法。

一次指数平滑可以克服移动平均法的缺点。但又平滑法进行预测，仍存在明显的滞后偏差。因此，也需要双指数平滑来弥补。公式为：

                                 

                                   

                                                           

在单指数平滑法基础上增加趋势信息，第二个等式描述趋势平滑过程，趋势的未平滑值使当前时刻平滑值si减去前一时刻平滑值si-1,再引入参数β对趋势进行一次指数平滑处理。

表 2-1：平滑预测比较（以北京市GDP为例）（单位：亿元）

年份	真实GDP	一次平滑	二次平滑	双指数平滑
2001	3861.5			3861.5
2002	4525.7			5189.9
2003	5267.2			5904.345
2004	6252.5			6806.441
2005	7149.8			7757.643
2006	8387.0	5907.283		8946.247
2007	10425.5	7001.283		10781.69
2008	11813.1	8215.85		12547.92
2009	12900.9	9488.133		14027.88
2010	14964.0	10940.05		15939.83
2011	17188.8	12613.22		18195.55
2012	19024.7	14386.17	10440.78	20365.73
2013	21134.6	16171.02	11969.07	22621.1
2014	22922.6	18023.17	13603.63	24690.22
2015	24779.1	20002.87	15356.08	26664.67
2016	27041.2	22015.73	17202.03	28839.42
2017	29883.0	24131.43	19121.73	31504.23
2018	33106.0	26478.32	21137.09	34688.4
2019	35445.1	28863.4	23252.49	37563.54
2020	36102.6		36718.679	40060.33

这里双指数平滑的指数取0.5，0.3。结果显然比两次平均平滑法的效果好。

不同指数下的双指数平滑法

1.2多元回归分析

用回归方程定量地刻画一个应变量与多个自变量间的线性依存关系,称为多元回归分析（multiple linear regression),简称多元回归(multiple regression)。

多元回归分析是多变量分析的基础，也是理解监督类分析方法的入口！实际上大部分学习统计分析和市场研究的人的都会用回归分析，操作也是比较简单的，但能够知道多元回归分析的适用条件或是如何将回归应用于实践，可能还要真正领会回归分析的基本思想和一些实际应用手法！

回归分析的基本思想是：虽然自变量和因变量之间没有严格的、确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达形式。其模型基本表达式为:

          

样本表达：

                        

矩阵表达：

                            

1.3最小二乘法回归

在所有的回归方法中，最小二乘法回归（OLS）最为著名。而且它也是所有空间回归分析的正确起点。它可以尝试了解或预测的变量或过程提供一个全局模型并可创建一个回归方程来表示该过程。

最小二乘法的主要思想是通过确定未知参数（通常是一个参数矩阵），来使得真实值和预测值的误差（也称残差）平方和最小，其计算公式为：

                                                       

其中yi是真实值。如下图所示，就是最小二乘法的一个示例，其中红色为数据点，蓝色为最小二乘法求得的最佳解，绿色即为误差。
                                  

最小二乘法示意图

1.4 地理加权回归分析

空间数据在地理学、经济学、环境学、生态学以及气象学等众多领域中广泛存在。根据Tobler提出的「地理学第一定律」︰任何事物之间都是空间相关的，距离越近的事物之间的何怕大)士R2大。因此，不同于传统的截面数据，空间数据的空间相关性会导致回归关系的空间非平棕性(空同异质性)。为了探索空间数据的空间非平稳性，Brunsdon等(1996)首次提出了地理加权回归模型，设定如下:

其中，

                                                   

为空间地理位置函数。

 根据Tobler地理学第一定律，距离越近的事物之间的相关性越大。故对于一个给定的地理位置

，可以采用局部加权最小二乘法来估计，即

 其中，是在地理位置处的空间权重。令

 

则在处的局部最小二乘估计值为

 其中：

   由于地理加权回归模型中的回归参数在每个数据采样点上都是不同的，因此其未知参数的个数为n×(P+1)，远远大于观测个数n，这样就不能直接利用参数回归估计方法估计其中的未知参数，而一些非参数光滑方法为拟合该模型提供了一个可行的思路。Foste & Gorr (1986）和Gorr & 0lligsehiaeger ( 1994）利用广义阻尼负反馈（generalized damped negative feedback）方法估计未知参数在各地理位置的值，这种估计方法只是在很直观的意义上考虑数据的空间结构，加之估计方法较为复杂，很难对估计量作深入的统计推断方面的研究。Brunsdon 等(1996）在局部多项式光滑思想上提出了偏差和方差折衷（Bias-Variance Trade-off）的解题思路:假设回归参数为一连续表面，位置相邻的回归参数非常相似在估计采样点i的回归参数时，以采样点i及其邻域采样点上的观测值构成局域子样，建立全局线性回归模型，然后采用最小二乘方法得到回归参数估计Bx(k=0.1，2，…,p）。对于另一个采样点，i+1采用另一个相应的局域子样来估计，以此类推。由于在回归分析过程中，以其它采样点上的观测值来估计i点上的回归参数因此得到的i点上的参数估计不可避免存在偏差，即参数估计为有偏估计。显然参与回归估计的子样规模越大，参数估计的偏差就越大，参与回归估计的子样规模越小，参数估计的偏差就越小。从降低偏差这一角度考虑因尽量减少子样规模，但子样规模的减少必然导致回归参数估计值的方差增加，精度降低。

1.5 Moran指数分析

莫兰指数分为全局莫兰指数（Global Moran's I）和局部莫兰指数（Local Moran's I），前者是Patrick Alfred Pierce Moran开发的空间自相关的度量；后者是美国亚利桑那州立大学地理与规划学院院长 Luc Anselin 教授在1995年提出的。

莫兰指数是一个有理数，经过方差归一化之后，它的值会被归一化到 -1.0 与 +1.0 之间。Moran's I大于0时，表示数据呈现空间正相关，其值越大空间相关性越明显；Moran's I小于0时，表示数据呈现空间负相关，其值越小空间差异越大；Moran's I为0时，空间呈随机性。

其定义如下：

通常情况，先做一个地区的全局I指数，全局指数只是告诉我们空间是否出现了集聚或异常值，但并没有告诉我们在哪里出现。换句话说全局Moran'I只回答Yes还是NO；如果全局有自相关出现，接着做局部自相关；局部Moran'I会告诉我们哪里出现了异常值或者哪里出现了集聚，是一个回答Where的工具。

二、数据处理

2.1 数据参数设计

        

2.2 空间自相关

根据地理学第一定律，空间上的事物都是有相关性的，离得越近相关性越强 ；离得越远相关性越弱。测试空间上某点的观测值是否与相邻点的值存在相关性，就是空间自相关的含义。空间自相关可以从定性和定量两个方面理解。现有多种指数可以量化空间自相关，最主要的两种指数为 Moran’I 指数和 Geary’C 指数,本次研究主要聚焦于Moran’I 指数。

空间自相关包括全局和局部两个层面。全局空间自相关是对属性值在整个区域的空间特征描述，局部空间自相关反映区域经济空间差异的变化趋势。空间自相关的结果会直接给出该数据的分布特征，即聚集、分散还是随机。

（1）全局空间自相关

全局空间自相关是在整个研究范围内分析指定的属性是否具有自相关性。根据整体分布状况判断某现象在空间是否有聚集特性存在，但不能确切地指出聚集在哪些地区以全局空间自相关的 Global Moran’I 为例，经过方差归一化之后，I 值在 [-1,1] 之间 ：若 I 值 >0，表示数据呈空间正相关性，在空间上呈现聚集状态，具体表现为高值与高值聚集，低值与低值聚集。此时，I值越大，空间相关性越明显。若 I 值 <0，表示数据呈空间负相关性，在空间上呈现分散状态，具体表现为高值排斥其他高值，倾向于靠近低值，或低值排斥其他低值，倾向于靠近高值。若 I 值 =0，表示数据呈随机状态，在空间上没有明显的分布规律，空间相关性不明显。另外，该工具还给出 z 得分和 p 值，对 I 值的显著性进行评估。Global Moran’I 公式如下 ：

在本次研究中，n 表示省级行政区个数，w（i,j）表示 n×n 的空间权重矩阵（可用邻接性或空间距离阈值构造，w（i,j） 的值为 0 或 1），xi 表示某省的GDP 观测值。

以 I 值判断全国GDP 整体的空间自相关性 ：若I 值显著为正，表明人GDP 较高（或较低）的地市在空间上集聚，I 值越接近 1，总体空间差异越小 ；若 I 值显著为负，表明GDP 较高的地市较分散， GDP较高的地市附近普遍是GDP 较低的地市，I 值越接近 -1，总体空间差异越大 ；若 I 值接近 0，表明GDP 在空间上随机分布，没有明显规律。

（2）局部空间自相关

局域空间自相关主要研究每个区域与其周边地区之间的关联性，分析空间分布的异质性。本论述采用 Local Moran's I，Moran 散点图描述的是变量与其空间滞后（即该观测值周围邻居的加权平均）向量之间的相关关系。横坐标为各单元标准化处理后的属性值，纵坐标为其空间连接矩阵所决定相邻单元的属性值的平均值。其分为四个象限，第一象限代表高观测值区域被同是高值的区域所包围（HH）；第二象限代表低值被高值包围（LH）；第三象限代表低值被低值包围（LL）；第四象限代表高值被低值包围（HL）。位于一三象限的空间单元存在较强的空间正相关，表示区域的集聚性和相似性；位于二四象限的空间单元存在较强的空间负相关，反应区域的异质性。Local Moran’I公式如下：

                                                        

其中，

                                                              

                                                              

                                                            

为空间权重值，n为研究区域上所有地区的总数，Ii则代表地i个地区的Local Moran’I指数,其中各项式子及其含义以表格方式呈现如下：

Local Moran’I指数各项式子及其含义

本次研究聚焦于2016-2020年间各个省份地区（不包括海南、香港、澳门、台湾等省份或特别行政区，下同）的GDP增长率及GDP总量 Global Moran’ I指数和Local Moran’ I指数，探究我国GDP分布及GDP增长的空间自相关性的程度。

3.3.1 GDP增长率

利用空间统计分析软件GeoDA分别计算了中国2016～2020这五年的全国各个省份GDP Global Moran’ I指数，并绘制出各年度的变化趋势图，结果见图1所示。

从表可以看出，计算出来的I值均大于0,且2016-2019年间的指数值大约都在0.1附近，说明这4年间，全国各省级行政区的GDP在整体上呈现一定程度的聚集状态，即GDP增长较高（或较低）的省份，其周边的省份GDP增长也较高（或较低）。这一现象十分正常，因为各个省份的经济发展模式、主体经济行业都各不相同，且其经济模式一定程度上受到地理空间条件的制约，因此会在地理空间上呈现一定聚集状态。但2020年，全国GDP增长率Global Moran’ I指数骤降到0.023左右，已经接近于0，说明该年份的GDP增长率几乎均匀分布，无明显的空间自相关性。考虑2020年是由于新冠疫情的影响，全国经济遭受重创，经济增长迟缓，但同时，由于国家疫情防控到位，及时采取相关措施控制疫情流行，2020年新冠疫情没有大规模扩散，收到严重影响的只有湖北省，这一点从2020年全国各省份Global Moran’ I指数统计图（如图3-2）也可以直观地看出，各省份除湖北省外在统计图上的位置均较为集中。

2020年全国各省份Global Moran’ I指数统计图

具体到局部的Moran’ I指数，五年间的全国各个省份GDP局部聚集图如所示

五年间的全国各个省份GDP局部聚集图

其中红色省份地区为“高-高”区域，即该地区的GDP增长率高，且周边地区的GDP增长率也高。

2.3 疫情及其经济损失的影响因素分析（OLS+GWR）

本节我们会分别通过最小二乘法回归（OLS）和地理加权回归(GWR)对8-10个变量进行分析，因变量统一为2019-2020GDP增长率相较于2018-2019GDP增长率的相对变化率。

OLS部分：

为了寻找哪些因素会在疫情背景下影响GDP，选取了以下十个作为自变量进行最小二乘法回归拟合（OLS）:

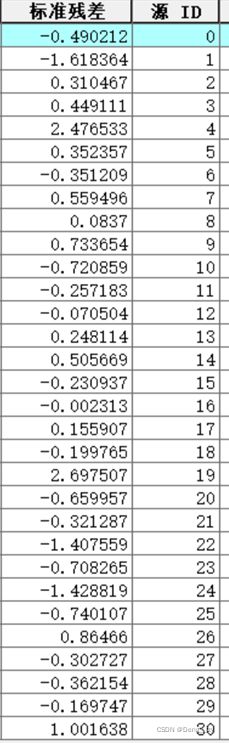
1.最小二乘法回归标准残差分布：

可以看出，除了广东省之外，整体的标准残差维持在了一个较小的区间范围内（尤其是中西部地区），湖北由于疫情较为严重，所以在图中处于一个较为特殊的值（周围较均明显低于其）。这保证了后续的分析具有一定的可靠性。

2.整体结果概览：

OLS结果汇总-模型变量

除了相对疫情指数外，其余几个指标的概率[b]均过高,显示出结果可靠性欠佳。

七个字段的说明及意义如下：

（1）系数[a]

    回归分析的系数代表了每个自变量对因变量的贡献度，系数的绝对值越大，表示该变量在模型里面贡献越大，也表示了该自变量与因变量的关系越紧密。

    另外这些系数的值表明了自变量与因变量的关系，比如S（总出口）的系数为0.58，则表示当总出口每增加一个单位，在其他自变量的值不发生改变的时候，因变量财政收入会增加0.58个单位。

    而且这个系数也表示了自变量与因变量之间的关系类型，即它分为正向和负向，系数为正，表示正相关，系数为负，表示负相关。不管是正向大还是负向大，越大，表示与因变量的关系强度越大，只不过是正相关还是负相关的问题。该参数是整个回归模型里面最重要的参数，没有之一。

（2）回归系数的标准差

    回归的标准误是模型中随机扰动项（误差项）的标准差的估计值。它的平方误差项的方差的无偏估计量，实际上又叫做误差均方，等于残差的平方和/（样本容量-待估参数的个数）。这个值越小，表示模型的预测越准。

（3）t统计量

    在统计学里面，t统计量是假设检验的重要枢轴量，多用于两样本均值检验，回归模型系数显著性检验。

T-Statistic=平均值 / 标准误

一般来来说，这个值表示，与P-value意义差不多，都是在验证零假设的情况下，模型的显著性，但是有些时候P-value会有一些问题，比如丢失一些信息。计算机里面进行统计验证的时候，T统计量越大，表示越显著。

（4）、概率[b]：

    这个就是P值,用来表示系数是否具有统计学上的显著性，越小则显著性越高。

（5）、（6）、（7）：Robust_SE Robust_t Robust_Pr [b]这三个字段，分别表示了标准差的健壮度、T统计量的健壮度和概率的健壮度。

在统计学里面，Robust Test通常被翻译稳健性检验，一般来说，就是通过修改（增添或者删除）变量值，看所关注解释变量的回归系数和结果是否稳健。

3.标准残差图：

标准残差的分布近似符合正态分布，说明拟合模型效果尚可。

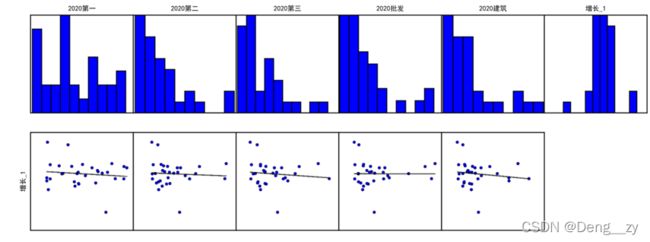
4.变量分布和关系：

这里会根据每组变量，形成一个自变量的分布柱状图（第一排）以及自变量和因变量组成的散点和回归图（第二排）。

首先要注意的是，OLS对自变量的分布是不是正态的，并不关心，但是如果Jarque-Bera统计量的P值指示，结果出现了偏差（也就是说残差的分布不平衡），那么说明自变量的分布，可能影响到了回归模型，所以这种情况下，我们可以尝试对某些偏差严重的自变量进行一些变换，然后重新建模验证（比如进行Log变换等）。

理论上，进行回归分析，每个自变量应该都要与因变量有相关性，如果某组出现了非线性，则表示此自变量无法对因变量进行解释，要么剔除掉，要么需要进行变换。

图 3-7：残差与预测图

从理论上来说，预测值和残差值应该没有任何的相关性，因为任何预测和残差的情况的产生都是随机的，这样才是最优，如果出现了相关性，就表示某些残差的出现是有规律的，这样就表示模型出现了偏差。

可以看出，本次最小二乘法回归的残差分布较为随机，说明结果具有一定的可靠性。

结论：由于自变量本身数量级的巨大差异性，我们难以从系数方面分析各类因素对GDP增长率的相对变化率的影响，而且OLS本身也并并不能从空间异质性的角度分析出有价值的结论，接下来我们会利用地理加权回归模型进行进一步分析。

GWR部分：

仿照最小二乘法的系数选择，由于GWR分析的特殊性，为保证数据的多重共线性、自相关性等维持在一个较低的水平，在剔除了2020建筑业增加值和2020批发零售增加值后，对剩余的八个属性进行回归分析。

因变量仍为2019-2020GDP增长率相较于2018-2019GDP增长率的相对变化率。

预备知识：GWR相关结果含义解读：

Predicted

对因变量的预测值：这些值是由 GWR 计算所得的估计（或拟合）y 值。这个值一般用来和因变量进行对比，越接近，表示拟合度越高。

Coefficient Intercept

截距：与Y轴的交点，这里的截距为负，表示观测值小于预测值。

Coefficient

各样本的各个自变量的系数。GWR的特点就在这里，不同于OLS，GWR会给出每个位置每个自变量的系数。

Residual

残差，就是观测值与预测值的差。

Standard Error

标准误

不是标准差，标准差的英文是：standard deviation）：衡量的是我们在用样本统计量去推断相应的总体参数（常见如均值、方差等）的时候，一种估计的精度。

Standard Error Intercept

标准误的截距：标准差与Y轴的交点。

Standard Error Coefficient

各自变量系数标准误：参考标准误的解释。在这里，这些值用于衡量每个系数估计值的可靠性。标准误与实际系数值相比较小时，这些估计值的可信度会更高。较大标准误差可能表示局部多重共线性存在问题。

Std. Residual

标准化残差：这个值也是ArcGIS进行GWR分析之后，给出的默认可视化结果。标准化残差的平均值为零，标准差为 1。在 ArcMap 中执行 GWR 时，将自动将标准化残差渲染为由冷色到暖色渲染的地图。官方说法是，请检查超过2.5倍标准化残差的地方，这些地方可能是有问题。

参数列表如下：

参数方面，可以看到R2普遍维持在0.49以上，系数截距普遍维持在-12左右，观测值与预测值差距不大 ，结果较为可靠：

                                     

可以看出，除西藏和吉林外，其余地区的标准残差均在2.5倍标准差内，官方说法是，请检查超过2.5倍标准化残差的地方，这些地方可能是有问题。从这个角度来看拟合效果较为准确，大部分地区的拟合结果可以采信，从而保证了后续的结果分析具有一定的可靠性。

1.R2分布：

在社会学分析中，R2在0.5左右已经是较好的拟合模型了。本次的地理加权回归中各省R2均位于0.5附近，且由西北内陆向东南沿海递增，呈现出一定的空间分布变化规律，说明拥有较好的拟合效果，后续分析结果可采纳，同时也体现出GWR回归分析的必要性。

3.疫情对各省级行政区GDP的影响系数分布：

由影响系数均为负可以看出，疫情对各省级行政区GDP均产生了负面影响，这一点符合常识。且这种影响呈现出一定规律的的空间异质性，即由东北至西南影响逐渐变大，但总体维持在了一个相对稳定的水平。具体原因可能是因为国家层面通过宏观调控等手段有效控制了疫情对地区经济发展带来的影响，所以单从疫情方面来分析可能不能得到较好的分析结果，故接下来将分析其他因素对GDP的影响。

4.失业率对各省级行政区GDP的影响系数分布：

 由上图可以看出失业率对各省级行政区GDP的影响，可以看出，这种影响整体上右东部至西部逐渐增强，在中西地区，由于失业率的上升，在疫情之下对GDP产生了不小的冲击，具体原因可能是这些地区劳动力较为集中，GDP对劳动力依存度比较高，疫情背景下失业率上升对该种经济结构的地区经济影响较大，相比较而言东部地区经济结构对劳动力依存较小，故失业率对GDP造成的影响相较于中西部地区较小。

5.出口额对各省GDP影响分布：

可以看到，相比于其他疫情不那么严重的地区，在受疫情影响较为严重的湖北、河南等地，出口额并未对GDP增长造成大的损失。猜测原因一方面是国家政策的倾斜，如鼓励湖北产的商品出口、周围省份可出口廉价产品支援湖北等；另一方面，可能这些省份本身的出口额占GDP比重并不大，故出口额变化对GDP无大的影响。整体影响的变化趋势是从东北至西南逐渐变大。推测疫情导致工厂关门、工业产出下降，进而导致出口额降低幅度较大，而这些省份经济较为依赖出口，故出口额下降对GDP影响较大。

6. 进口额对各省GDP影响分布：

和上面的出口额进行对比，可以很明显发现二者变化趋势的差异性。进口额变化对GDP的影响程度是由东南沿海向西北内陆递减。沿海地区交通发达，对进口商品依存度大（外省进口以及国外进口）而疫情极大的影响力这些地方的商品进口，进而对GDP产生了较大的影响。相反地，内陆地区本就对进口依存度不高，故在疫情大背景下GDP受影响程度不高。进口和出口额地理空间分布趋势的差异性也可反映出地理加权回归的显著优势。

7.工业产出对各省GDP影响分布：

我们知道，在东北老工业基地相关省份，工业占比大，这些地方的工业产出对GDP影响比重显著高于其他省，而在疫情大背景下，许多工厂停产，工业产出大大下降，进而对GDP产生了较为显著的损失影响。西南地区工业产值占比小，故其浮动对GDP影响较小。

附表：

             

                                               

第一、二、三产业附加值对各省GDP影像系数

结论：

国民生产总值（GDP）是一个相当复杂的结果，其受相当多的因素的影响，疫情确实是其中的一个显著因素，但许多时候疫情并不直接影响经济，而是通过影响进出口额度或工业产出等方面来间接影响GDP。要研究清楚疫情究竟怎样影响GDP，需要在对经济学原理有着深刻认识的条件下，通过大量数据的分析，并通过大量的方法比较才有可能得到比较有价值的结果。很显然，单从一个地理加权回归分析并不能获得理想中的结果，只能从某些方面对结果窥知一二，得出一些推测层面的简单结论。

2.4 疫情及其对各省经济发展的总体影响

     2020年年初国内爆发的新冠疫情使国内各省各地区的生产和生活收到普遍冲击，但各省表现不一样，国内疫情主打以湖北省为中心展开传播。

     由图可以看出，全国疫情分布基本上以湖北为中心，进行传播。经计算各省相对疫情指数indexi和GDP损失率Lossi其计算公式为：

                                                         

                                         

将计算出的结果进行统计，各个列出位于前十的省市：

表 3-5：相对疫情与GDP损失率排前十的省市

序 号	疫情情况		经济情况
	省市	相对疫情	省市	GDP损失率
1	湖北	11.86%	湖北	16.134%
2	黑龙江	0.30%	青海	10.257%
3	北京	0.27%	新疆	9.959%
4	上海	0.26%	北京	9.876%
5	江西	0.21%	上海	9.796%
6	浙江	0.19%	陕西	9.795%
7	重庆	0.17%	天津	9.405%
8	海南	0.16%	广东	9.290%
9	安徽	0.16%	河南	9.198%
10	湖南	0.15%	内蒙古	9.143%

直观的分布图如下：

相对疫情分布

GDP损失程度分布

OLS报表：

 以上结果显示二者确实存在一定的相关性，可见从整体而言疫情对GDP产生了不小的影响。

例如，湖北疫情是国内最严重的。北京、上海等地区因为区域小，人口规模不大，基数相对较小和疫情传播更聚集，导致相对疫情较严重。湖南、安徽、重庆、江西距离湖北较近，受到的波及较大。

就经济发展方面，湖北因为疫情导致的封城必然会受到非常大的经济冲击。青海、新疆、陕西、内蒙古因为产业链单一，在特殊情况下，难以做到变通适应，导致了一定性质上的经济损失。北京、上海、广东、天津等省市因为地区盛世繁荣，在这一特殊情况下，要想达到预期的经济发展确实有一定难度。

三、结论

GDP无疑是国民经济核算的核心指标和衡量一个国家或地区经济状况和发展水平的最重要指标，长期以来各派学者对GDP影响因素的研究络绎不绝。本文站在地理空间分析的角度，简略分析了新冠疫情这一大背景下GDP受到了怎样的影响以及被哪些因素影响。由于GDP是一个相当复杂的结果，所以我们所做的研究只能算是窥探性或者说是验证性的研究。

总的来说，疫情对GDP的影响是负面的，这一点从预测分析和多元分析方面都可以窥见——几种预测模型都显示实际值低于预测值，基于此预测值计算的GDP损失程度确实与相对疫情指数存在着一定的相关性；后续的多元回归分析进一步印证了这一点，即疫情虽然对某些行业发展利好（如医疗、某些电商行业等），但是总体上仍然对中国的经济发展产生了不小的影响。从地理加权回归分析的结果来看，不同因素对GDP的影响有着不小的空间异质性，这种异质性时常存在着某些规律，而且不同因素所呈现的空间变化规律有时是截然相反的。这种异质性的来源可能与地区自身的发展水平、人口、地理位置、经济结构等等有关（例如某些省份经济结构单一，受疫情冲击影响大），在处理这种空间异质性时，就可以体现出空间分析的必要性和强大威力，也是空间分析与其他类型分析的不同之处。

GDP是一个宏大的主题，这也导致了GDP本身受到的影响因素实在过多，所以在分析的时候，有时并不能得到理想中的结论。例如国家为了减小疫情下经济发展的不平衡、减小差异，会对某些疫情严重的省份给予政策上的倾斜，例如进出口商品政策的倾斜、税率的调整、土地政策的倾斜等等。而我们在一般的分析中很难将这种政策倾斜考虑在内，这就会使得结论在意料之外；此外，GDP也会受到近几年来中美贸易战的影响，所以只以近三年GDP数据得到的增长率的相对变化率作为因变量会显得说服力没有那么强（因为贸易战也会在许多方面影响GDP，需要对其与疫情造成的GDP影响通过某些方法加以区分）；有时也会受困于我们自身对经济学原理认识的不足而难以从获得的数据中分析出有价值的结论，这也是本研究目前存在的不足。

由此可知，本次研究下一步的改进方法是扩大搜索面，考虑包括国家政策、政治环境等在内的更多因素对GDP的影响，并通过合适的筛选分批对自变量进行处理，以此得到多项结论，通过合适的方法评判可靠性后综合得出结论。