前言
拟合在数学建模中应用普遍,而最小二乘拟合又是常用的拟合方法。
数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合(fitting)。 --摘自百度百科
最小二乘拟合,我们从原理出发,给出三个示例并结合python代码,从而加深对最小二乘拟合的理解。
1.原理
首先最小二乘拟合是一种思想,通过最小二乘拟合可以进行线性拟合,多项式拟合,指数拟合...等任意形式拟合。
拟合:拟合用于解决对于一系列已知的\(x_i,y_i\)求\(y=f(x)\)方程的问题。
最小二分思想:我们通过拟合找到\( \phi(x) \),使得误差平方和Q=\(\sum(\phi(x_i)-y_i)^2\)最小,则认为\(\phi(x)\)近似等于我们需要的\(f(x)\)。使误差平方和Q=\(\sum(\phi(x_i)-y_i)^2\)最小的原则就是最小二分思想。
\(\phi(x)\)的表达式:如何求\(\phi(x)\)呢,可以根据已知xi,yi画出的图像走势,选择\(\phi(x)=f(e^x),\phi(x)=f(x^n)+f(x^{n-1})+....\)等方程式进行拟合。此时产生一些参数如\(a*e^x+b\)中的a,b。
误差平方和Q:那么Q的最小值如何求呢?首先引入高等数学的内容
$$ \begin{cases} Q_a=0\\ Q_b=0 \ &+函数连续\Rightarrow求出极值点+边界点\Rightarrow最值点\\ Q_c=0\\ ...... \end{cases} $$
有极值的充分条件是Q关于a,b,c...的偏导等于0且Q式连续。
而最值通过极值和边界值比较确定。
这里求Q的最小值,通过求Q关于a,b,c...的偏导等于0,可求得a,b,c...参数,从而求Q的值。有n个方程n个未知数,可以求解。
所以根据a,b,c...等参数的值,可得到\(\phi(x)\)的方程,并用来画图比较拟合预测值和真实值。
2.python代码
-多项式拟合
主要是对np.polyfit和np.poly1d的使用。
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]#这两行解决字体问题
x = np.arange(1, 101)#改数据
y = np.array([11, 5, 4, 7, 6, 6, 5, 7, # 改数据
13, 6, 5, 7, 12, 5, 4, 6,
9, 5, 5, 11, 29, 21, 17, 20,
27, 13, 9, 10, 16, 6, 5, 7,
11, 5, 5, 6, 12, 7, 7, 10,
15, 10, 9, 11, 15, 10, 10, 16,
26, 21, 23, 36, 50, 45, 45, 49,
57, 43, 40, 44, 52, 43, 42, 45,
52, 41, 39, 41, 48, 35, 34, 35,
42, 34, 36, 43, 55, 48, 54, 65,
80, 70, 74, 85, 101, 89, 88, 90,
100, 87, 88, 89, 104, 89, 89, 90,
106, 96, 94, 99])
z1=np.polyfit(x,y,deg=100)#deg=100,100次多项式,返回值为系数
p1=np.poly1d(z1)#通过多项式系数,返回方程
print(p1)#输出方程
print(np.polyval(p1,12))#进行预测
print(np.polyval(z1,13))#这两种方法都可以,可以p1,或者z1作为参数,12,13为x,输入x得到预测值
y_pred=p1(x)#预测值
plt.plot(x,y,'*',label='origin value')
plt.plot(x,y_pred,'r',color='green',label='pred value')
plt.title('多项式拟合')
plt.xlabel('xlable')
plt.ylabel('ylabel')
plt.legend(loc=3, borderaxespad=0., bbox_to_anchor=(0, 0))#画出图例
plt.show()有兴趣可通过调整多项式次数,研究过度拟合的情况,这里不过多阐述。下面是多项式拟合情况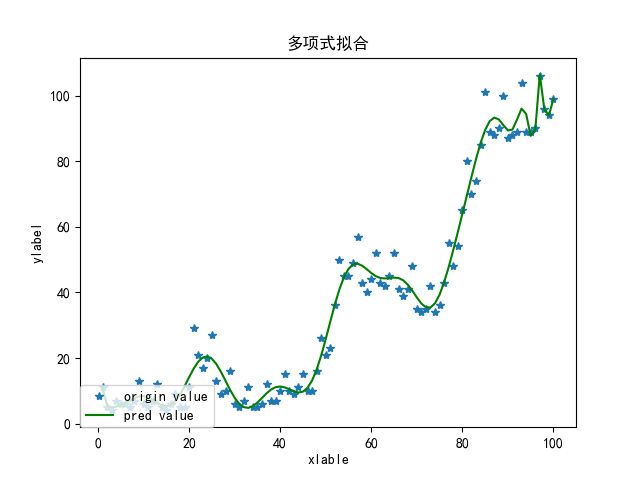
-任意形式的拟合
指数拟合
上一种拟合方法还不能对\(f(e^x)\)等其他形式的方程进行拟合,下面主要通过plt.cur_fit来进行拟合。查阅函数并注意函数返回类型。
代码中fun()函数可以设置任意我们想要的函数,从而达到以任意形式拟合。
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]#这两行解决字体问题
def fun(x,a,b,c,d,e):#自定义任意类型的函数
return a*np.exp(x)+b*x+c
#return a*b**x+c+d/np.exp(x)+e/x**5;
if __name__=="__main__":
x = np.arange(1, 105)
y = np.array([11, 5, 4, 7, 6, 6, 5, 7,
13, 6, 5, 7, 12, 5, 4, 6,
9, 5, 5, 11, 29, 21, 17, 20,
27, 13, 9, 10, 16, 6, 5, 7,
11, 5, 5, 6, 12, 7, 7, 10,
15, 10, 9, 11, 15, 10, 10, 16,
26, 21, 23, 36, 50, 45, 45, 49,
57, 43, 40, 44, 52, 43, 42, 45,
52, 41, 39, 41, 48, 35, 34, 35,
42, 34, 36, 43, 55, 48, 54, 65,
80, 70, 74, 85, 101, 89, 88, 90,
100, 87, 88, 89, 104, 89, 89, 90,
106, 96, 94, 99, 109, 99, 96, 102])
popt,pcov=curve_fit(fun,x,y)#popt返回值是残差最小时的参数,即最佳参数
y_pred=[fun(i,popt[0],popt[1],popt[2],popt[3],popt[4]) for i in x]#将x和参数带进去,得到y的预测值
print(popt)#输出参数
plt.plot(x,y,'*',label='original values')
plt.plot(x,y_pred,'-',label='pred values',color='green')
plt.xlabel('xlabel')
plt.ylabel('ylabel')
plt.title('指数拟合')
plt.legend(loc=3, borderaxespad=0., bbox_to_anchor=(0, 0))
plt.show()下面是指数函数拟合的情况,因为数据问题差距有点大,不过明白原理不用在乎这些细节了。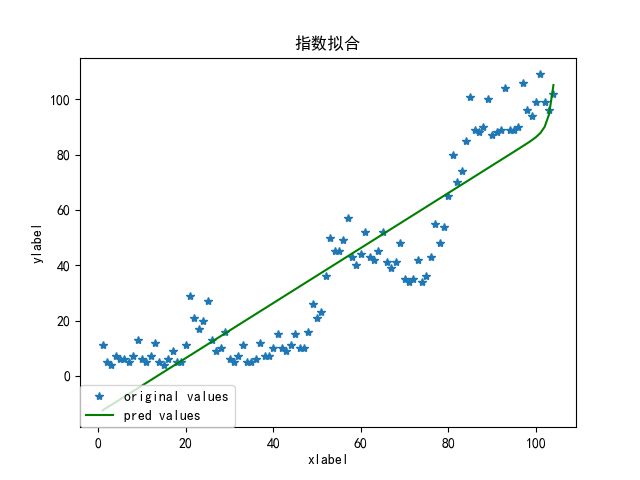
幂函数拟合
下面更换fun函数即可完成幂函数的拟合,这里我顺带换了一下数据。
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"]#这两行解决字体问题
def fun(x,a,b,c,d,e):#自定义任意类型的函数
return a/x+b
#return a*np.exp(x)+b*x+c
#return a*b**x+c+d/np.exp(x)+e/x**5;
if __name__=="__main__":
x = np.arange(1, 6)
y = np.array([1,0.78,0.61,0.55,0.42])
popt,pcov=curve_fit(fun,x,y)#popt返回值是残差最小时的参数,即最佳参数
y_pred=[fun(i,popt[0],popt[1],popt[2],popt[3],popt[4]) for i in x]#将x和参数带进去,得到y的预测值
print(popt)#输出参数
plt.plot(x,y,'*',label='original values')
plt.plot(x,y_pred,'-',label='pred values',color='green')
plt.xlabel('xlabel')
plt.ylabel('ylabel')
plt.title('幂函数拟合')
plt.legend(loc=3, borderaxespad=0., bbox_to_anchor=(0, 0))
plt.show()好了,到此结束~
记录一下我的第一次撰写博客,以后再接再厉~
