第五章-系统的频域分析
为什么对系统频域分析：
连续系统的频率响应：
频率响应H(jw).输出和输入频谱之比,也就是时域冲激响应h(t)的傅里叶变换。
H(jw)反映了系统的频域特性
H(jw) = Y/X = [bm(jw)m+…]/ [an(jw)n+…]=F[h(t)]
an,bm是系统的微分方程Y和X的系数
特点
三角类函数进入系统后，输出的是一个幅值和频率改变的三角函数，
计算方法
如何计算H(jw)
1. h(t) 的傅里叶变换
H(jw) =F[h(t)]
2. 由微分方程
H(jw) = Y/X = [bm(jw)m+…]/ [an(jw)n+…]
3. 实际电路的频域等效电路
电容：1/jwC
频域关系： Yzs(jw) = X(jw) ·H(jw)
利用这个等式可以求时域或者频域下的输出。
例子：
已知x(t),系统微分方程，求yzs：(零状态响应)
由x(t)得到X(jw), 由微分方程得到H(jw) = Y/X = [bm(jw)m+…]/ [an(jw)n+…]; 由上方等式得到Y(jw)，傅里叶反变换得到y(t)
一方面，和时域的卷积运算相比，简化了运算，但这不是主要目的，因为由Y得到y的过程可能会比较难，x(t)如果不收敛，也不能求出X(jw)
第二，可以看出三者之间的关系。
H物理意义
输出变为H(jw)X(jw), 输出和输入相比的变化，完全由H(jw)确定。
如果从频谱图上来看，H(jw)会对一些频率上的数据放大，提前，抑制，延后。
因此有的系统可以看出滤波器，模拟滤波器和连续滤波器
频域分析特点：
优点：求解系统的零状态响应时，可以直观地体现信号通过系统后信号频谱的改变，解释激励与响应时域波形
的差异，物理概念清楚。
不足：
（1）只能求解系统的零状态响应，系统的零输入响应
仍需按时域方法求解。
（2）若系统频率响应(或激励信号)的傅里叶变换不存在，
则无法利用频域 分析法。
解决方法：采用拉普拉斯变换
几个重要的系统
无失真传输系统
失真分类：
非线性失真：产生新的频率,比如加入噪声
线性失真：不产生新的频率（幅值，相位），比如加入延时
无失真传输系统
任何信号输入后的输出都不失真：
y(t)= K·x(t-t0)
h(t) = Kδ(t-t0)
H(jw) = K e^-w td^
特点：系统带宽无穷大；相位响应和w成线性关系。
例子：
H(jw) = (1-jw)/(1+jw) = e-2arctan(w)
不是无失真系统，它会使输入产生线性失真（幅值不失真，相位失真）
如输入sin(x)和sin(3x)，输出的幅值变化相同，但是相位变化不同。
如输入sin(x)+sin(3x)，输出的信号会有较大不同。
滤波器
四种
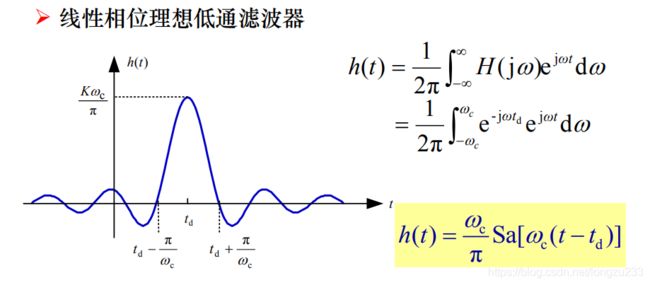
理想低通滤波器
频域：
幅度响应理想通断
相位响应为线性函数 相位= -td w, 斜率是-td
时域：
如果没有延迟，h(t)就是上面的图左移，是一个Sa函数（抽样函数），这个函数和冲激函数很像（冲激函数是中间无穷大，其他为0），但是有差别，说明有失真，增大wc可以减小失真。
时域上存在t<0的值，所以是非因果系统，物理不可实现。
真实滤波器
连续信号的调制与解调
为何要调制？
- 将低频信号搬移至较高的频段，方便无线发射。
- 不同信号可以使用不同频段，充分利用信道。
怎么调？
输入信号称为调制信号，调制信号乘上一个载波信号就是调制。
调制方法：
幅度调制；
频率调制。
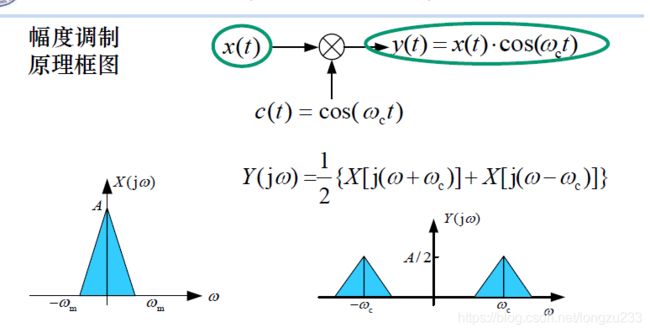
幅度调制：
调制信号的频率低，可以看乘常数，调制后：
对比调制信号和幅度调制信号可以发现，幅度调制信号的包络线就是调制信号，也就是说，调制信号的频率（音调）对应为幅度调制信号的幅值（响度）。
特点：
时域的相移对应频域的频移
调节Wc可以调节到不同的位置。
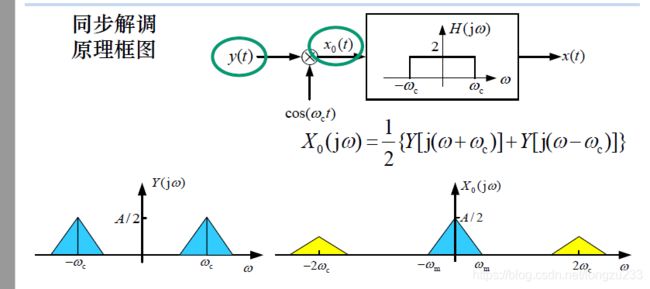
同步解调
再乘以同一个载波信号c(t)，然后通过低通滤波器。新的信号强度是原来的一半。
要求：发送端和接收到要 同频同相。
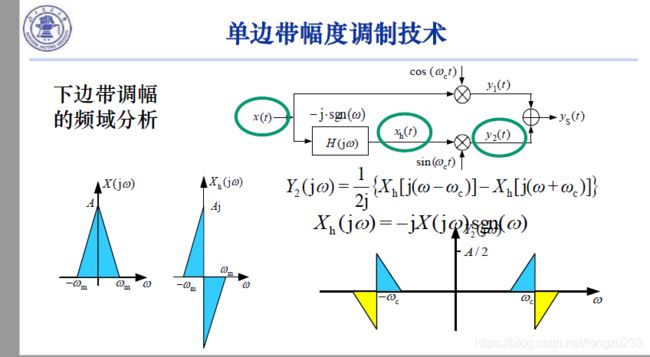
单边带幅度调制技术
可以只发送上边带（外围部分）或者下边带（内围部分）。提高频带利用率。
将调制好的信号通过带通滤波器，滤掉上边带或者下边带即可。
工程上没有理想带通滤波器，常常使用的是希尔伯特变换器。
希尔伯特
原理
频率调制：
调制信号改变载波信号的频率，调制信号为正时增加频率，为0时不改变频率，为负时减小频率。
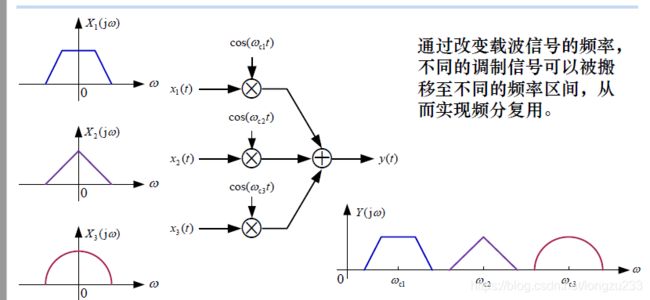
频分复用
同时传输多个低频信号。
能够充分利用信道的资源。
过程：
把低频信号调制到多个频道。解调时通过带通可以分别解调。
