数学建模：图论模型 — 最短路算法 (Dijkstra 算法与 Floyd 算法) 及 Python 实现

Dijkstra 算法 (求固定起点到其余各点的最短路)

Dijkstra 算法时寻求从一固定起点 $u_0$ 到其余各点的最短路最有效的算法之一, 由 E. W. Dijkstra 于 1959 年提出.

Dijkstra 算法的理论依据是一个重要而明显的性质: 最短路是一条路, 最短路上的任一子段也是最短路.

Dijkstra 算法的基本思想是：按距固定起点 $u_0$ 从近到远为顺序, 依次求 得 $u_0$ 到图 $G$ 各顶点的最短路和距离, 直至某个顶点 $v_0$ (或直至图 $G$ 的所有顶点).

步骤

设图 $G$ 有 $n$ 个顶点; 边的长度 ${\ell }_{ij}⩾0$; 若结点 $v_i$ 和 $v_j$ 不相连, 则令 ${\ell }_{ij}=\infty$, 对每个结点 $v_i$, 令 ${\ell }_{ii}=0$.

将顶点集 $V$ 分成两部分，一部分为具有 $P$（永久性）标号的集合，另一部分为具有 $T$（暂时性）标号的集合。
结点 $v$ 的 $P$ 标号是指从 $v_1$ 到 $v$ 的最短路径的长度；顶点 $u$ 的 $T$ 标号是指从 $v_1$ 到 $u$ 某条路径的长度。
Dijkstras 算法首先将 $v_1$ 取为 $P$ 标号，其余结点取为 $T$ 标号，逐步将具有 $T$ 标号的结点改为 $P$ 标号。当结点 $v_n$ 被改为 $P$ 标号时，就找到一条从 $v_1$ 到 $v_n$ 的最短路径。

• Step 1: 初始化

将 $v_1$ 置为 $P$ 标号, $d\left(v_1\right)=0,P=\left\{v_1\right\};\forall v_i(i\ne 1)$, 置 $v_i$ 为 $T$ 标号, 即 $T=V-P$, 且
$$\{\begin{array}{ll}d\left(v_i\right)=W\left(v_1,v_i\right),& \text{若}{v}_i{v}_1\text{相邻}\\ d\left(v_i\right)=\infty ,& \text{否则}\end{array}$$

• Step 2: 找最小

寻找具有最小值的 $T$ 标号的结点。若为 $v_l$，则将 $v_l$ 的 $T$ 标号改为 $P$ 标号，且 $P=P\cup \{v_l\}，T=T-\{v_l\}$。

• Step 3：修改

修改与 $v_l$ 相邻的结点的 $T$ 标号的值。 $\forall v_i\in T$ :
$$d(v_i)=\{\begin{array}{ll}d\left(v_l\right)+W\left(v_l,v_i\right)& \text{ 若 }d\left(v_1\right)+W\left(v_i,v_i\right)<d\left(v_i\right)\\ d\left(v_i\right)& \text{ 否则 }\end{array}$$

• Step 4：重复 (2) 和 (3)，直到 $v_n$ 改为 $P$ 标号为止。

示例

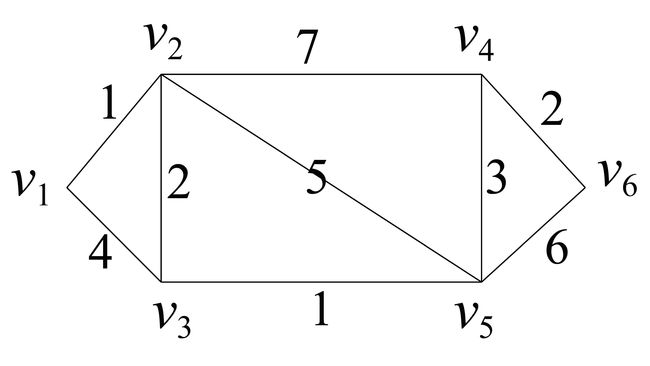
求无向图最短路

• Step 1:
  $P=\{v_1(0)\}$
  $T=\{v_2(1,v_1),v_3(4,v_1),v_4(\infty ),v_5(\infty ),v_6(\infty \}$
• Step 2:
  $P=\{v_1(0),v_2(1,v_1)\}$
  $T=\{v_3(3,v_1,v_2),v_4(8,v_1,v_2),v_5(6,v_1,v_2),v_6(\infty )\}$
• Step 3:
  $P=\{v_1(0),v_2(1,v_1),v_3(3,v_1,v_2)\}$
  $T=\{v_4(8,v_1,v_2),v_5(4,v_1,v_2,v_3),v_6(\infty )\}$
• Step 4:
  $P=\{v_1(0),v_2(1,v_1),v_3(3,v_1,v_2),v_5(4,v_1,v_2,v_3)\}$
  $T=\{v_4(7,v_1,v_2,v_3,v_5),v_6(10,v_1,v_2,v_3,v_5)\}$
• Step 5:
  $P=\{v_1(0),v_2(1,v_1),v_3(3,v_1,v_2),v_5(4,v_1,v_2,v_3),v_4(7,v_1,v_2,v_3,v_5)\}$
  $T=\{v_6(9,v_1,v_2,v_3,v_5,v_4)\}$
• Step 6:
  $P=\{v_1(0),v_2(1,v_1),v_3(3,v_1,v_2),v_5(4,v_1,v_2,v_3),v_4(7,v_1,v_2,v_3,v_5),v_6(9,v_1,v_2,v_3,v_5,v_4)\}$
  $T=\{\}$

即

$$\begin{array}{lcccccc}& v_2& v_3& v_4& v_5& v_6& \\ \mathrm{Step}1& 1(v_1)& 4& \infty & \infty & \infty & (v_2)第1短\\ \mathrm{Step}2& & 3(v_2)& 8& 6& \infty & (v_3)第2短\\ \mathrm{Step}3& & & 8& 4(v_3)& \infty & (v_5)第3短\\ \mathrm{Step}4& & & 7(v_5)& & 10& (v_4)第4短\\ \mathrm{Step}5& & & & & 9(v_4)& (v_6)第5短\end{array}$$

所以 $v_1$ 到各顶点的最短路径和距离分别为:
$v_2:v_1\to v_2(1)$
$v_3:v_1\to v_2\to v_3(3)$
$v_5:v_1\to v_2\to v_3\to v_5(4)$
$v_4:v_1\to v_2\to v_3\to v_5\to v_4(7)$
$v_6:v_1\to v_2\to v_3\to v_5\to v_4\to v_6(9)$

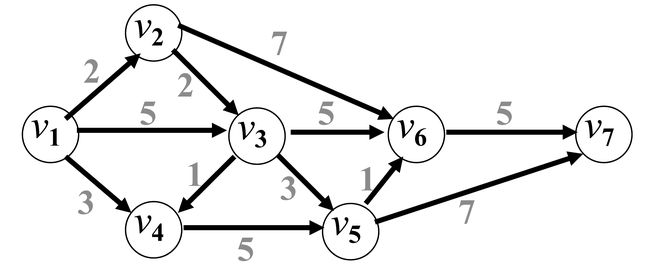
求有向图最短路

仿照上例

$$\begin{array}{cccccccr}& v_2& v_3& v_4& v_5& v_6& v_7& \\ \mathrm{Step}1& 2& 5& 3& \infty & \infty & \infty & 2\left(v_2\right)\text{ 第1短 }\\ \mathrm{Step}2& & 4& 3& \infty & 9& \infty & 3\left(v_4\right)\text{ 第2短 }\\ \mathrm{Step}3& & 4& & 8& 9& \infty & 4\left(v_3\right)\text{ 第3短 }\\ \text{Step }4& & & & 7& 9& \infty & 7\left(v_5\right)\text{ 第4短 }\\ \text{Step }5& & & & & 8& 14& 8\left(v_6\right)\text{ 第5短 }\\ \text{Step }6& & & & & & 13& 13\left(v_7\right)\text{ 第6短 }\end{array}$$

Python 实现

import numpy as np
def Dijkstra_all_minpath(matr,start): #matr为邻接矩阵的数组，start表示起点
    n=len( matr) #该图的节点数
    dis=[]; temp=[]
    dis.extend(matr[start])  #添加数组matr的start行元素
    temp.extend(matr[start]) #添加矩阵matr的start行元素
    temp[start] = np.inf  #临时数组会把处理过的节点的值变成 \infty
    visited=[start]  #start已处理
    parent=[start]*n   #用于画路径，记录此路径中该节点的父节点
    while len(visited)<n:
        i= temp.index(min(temp)) #找最小权值的节点的坐标
        temp[i]=np.inf
        for j in range(n):
            if j not in visited:
                if (dis[i]+ matr[i][j])<dis[j]:
                    dis[j] = temp[j] =dis[i]+ matr[i][j]
                    parent[j]=i  #说明父节点是i
        visited.append(i)  #该索引已经处理了
        path=[]  #用于画路径
        path.append(str(i))
        k=i
        while(parent[k]!=start):  #找该节点的父节点添加到path，直到父节点是start
            path.append(str(parent[k]))
            k=parent[k]
        path.append(str(start))
        path.reverse()   #path反序产生路径
        print(str(i)+':','->'.join(path))  #打印路径
    return dis

Floyd 算法 (求每对顶点间的最短路算法)

要求每对顶点间的最短路, 可多次使用 Dijkstra 算法, 每次以不同的顶点作为起点, 用 Dijkstra 算法求出从该起点到其余顶点的最短路径, 反复执行 $n-1$ 次这样的操作, 就可得到每对顶点之间的最短路. 但这样做需要大量的重复计算, 效率不高. R. W. Floyd 于 1962 年提出了一个直接寻求任意两顶点之间最短路的算法.

迭代方式

Floyd 算法是一个经典的动态规划算法, 其基本思想是递推产生一个矩阵序列 $A_1,A_2,\cdots ,A_k,\cdots ,A_n$, 其中矩阵 $A_k={\left(a_k(i,j)\right)}_{n\times n}$, 其第 $i$ 行第 $j$ 列元素 $a_k(i,j)$ 表示从顶点 $v_i$ 到顶点 $v_j$ 的路径上所经过的顶点序号不大于 $k$ 的最短路径长度.

计算时用迭代公式
$$a_k(i,j)=\min \left(a_{k-1}(i,j),a_{k-1}(i,k)+a_{k-1}(k,j)\right),$$

$k$ 是迭代次数, $i,j,k=1,2,\cdots ,n$. $A_0$ 为邻接矩阵, 当 $k=n$ 时, $A_n$ 即是各顶点之间的最短距离值.

路由矩阵

如果在求得两点间的最短距离时, 还需要求得两点间的最短路径, 需要在上面距离矩阵 $A_k$ 的迭代过程中, 引入一个路由矩阵 $R_k={\left(r_k(i,j)\right)}_{n\times n}$ 来记录两点间路径的前驱后继关系, 其中 $r_k(i,j)$ 表示从顶点 $v_i$ 到顶点 $v_j$ 的路径经过编号为 $r_k(i,j)$ 的顶点.

路由矩阵的迭代过程如下:

(1) 初始时
$$R_0=0_{n\times n}$$
(2) 迭代公式为
$$R_k={\left(r_k(i,j)\right)}_{n\times n},$$

其中
$$r_k(i,j)=\{\begin{array}{l}k,\text{ 若 }{a}_{k-1}(i,j)>a_{k-1}(i,k)+a_{k-1}(k,j),\\ r_{k-1}(i,j),\text{ 否则. }\end{array}$$

直到迭代到 $k=n$, 算法终止.

查找最短路径

查找 $v_i$ 到 $v_j$ 最短路径的方法如下:

若 $r_n(i,j)=p_1$, 则点 $v_{p_1}$ 是顶点 $v_i$ 到顶点 $v_j$ 的最短路的中间点, 然后用同样的方法再分头查找. 若

(1) 向顶点 $v_i$ 反向追踪得: $r_n\left(i,p_1\right)=p_2,r_n\left(i,p_2\right)=p_3,\cdots ,r_n\left(i,p_s\right)=0$;

(2) 向顶点 $v_j$ 正向追踪得: $r_n\left(p_1,j\right)=q_1,r_n\left(q_1,j\right)=q_2,\cdots ,r_n\left(q_t,j\right)=0$;

则由点 $v_i$ 到 $v_j$ 的最短路径为: $v_i,v_{p_s},\cdots ,v_{p_2},v_{p_1},v_{q_1},v_{q_2},\cdots ,v_{q_t},v_j$.

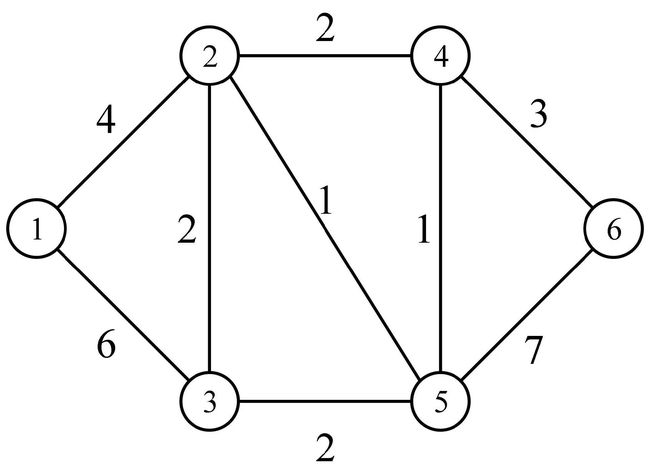
示例

迭代 0:
$$A_0=\left[\begin{array}{cccccc}0& 4& 6& \infty & \infty & \infty \\ 4& 0& 2& 2& 1& \infty \\ 6& 2& 0& \infty & 2& \infty \\ \infty & 2& \infty & 0& 1& 3\\ \infty & 1& 2& 1& 0& 7\\ \infty & \infty & \infty & 3& 7& 0\end{array}\right],R_0=(0{)}_{6\times 6}$$

迭代 1: $A_1$ 的元素 $a(i,j)$ 的意义为 $i$ 直接到达 $j$ 及经节点 1 到达 $j$ 的两种方式中, 最短路线的距离
$${\mathrm{A}}_1=\left[\begin{array}{cccccc}0& 4& 6& \infty & \infty & \infty \\ 4& 0& 2& 2& 1& \infty \\ 6& 2& 0& \infty & 2& \infty \\ \infty & 2& \infty & 0& 1& 3\\ \infty & 1& 2& 1& 0& 7\\ \infty & \infty & \infty & 3& 7& 0\end{array}\right],R_1=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

迭代 2: $A_2$ 的元素 $a(i,j)$ 的意义为 $i$ 直接到达 $j$ 及最多经节点 1, 2 到达 $j$ 的所有方式中, 最短路线的距离
$$A_2=\left[\begin{array}{cccccc}0& 4& 6& 6& 5& \infty \\ 4& 0& 2& 2& 1& \infty \\ 6& 2& 0& 4& 2& \infty \\ 6& 2& 4& 0& 1& 3\\ 5& 1& 2& 1& 0& 7\\ \infty & \infty & \infty & 3& 7& 0\end{array}\right],R_2=\left[\begin{array}{cccccc}0& 0& 0& 2& 2& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 2& 0& 0\\ 2& 0& 2& 0& 0& 0\\ 2& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

迭代 3:
$${\mathrm{A}}_3=\left[\begin{array}{cccccc}0& 4& 6& 6& 5& \infty \\ 4& 0& 2& 2& 1& \infty \\ 6& 2& 0& 4& 2& \infty \\ 6& 2& 4& 0& 1& 3\\ 5& 1& 2& 1& 0& 7\\ \infty & \infty & \infty & 3& 7& 0\end{array}\right],R_3=\left[\begin{array}{cccccc}0& 0& 0& 2& 2& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 2& 0& 0\\ 2& 0& 2& 0& 0& 0\\ 2& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

迭代 4:
$${\mathrm{A}}_4=\left[\begin{array}{cccccc}0& 4& 6& 6& 5& 9\\ 4& 0& 2& 2& 1& 5\\ 6& 2& 0& 4& 2& 7\\ 6& 2& 4& 0& 1& 3\\ 5& 1& 2& 1& 0& 4\\ 9& 5& 7& 3& 4& 0\end{array}\right],R_4=\left[\begin{array}{cccccc}0& 0& 0& 2& 2& 4\\ 0& 0& 0& 0& 0& 4\\ 0& 0& 0& 2& 0& 4\\ 2& 0& 2& 0& 0& 0\\ 2& 0& 0& 0& 0& 4\\ 4& 4& 4& 0& 4& 0\end{array}\right]$$

迭代 5:
$${\mathrm{A}}_5=\left[\begin{array}{cccccc}0& 4& 6& 6& 5& 9\\ 4& 0& 2& 2& 1& 5\\ 6& 2& 0& 3& 2& 6\\ 6& 2& 3& 0& 1& 3\\ 5& 1& 2& 1& 0& 4\\ 9& 5& 6& 3& 4& 0\end{array}\right],R_5=\left[\begin{array}{cccccc}0& 0& 0& 2& 2& 4\\ 0& 0& 0& 0& 0& 4\\ 0& 0& 0& 5& 0& 5\\ 2& 0& 5& 0& 0& 0\\ 2& 0& 0& 0& 0& 4\\ 4& 4& 5& 0& 4& 0\end{array}\right]$$

迭代 6 ($n$): 任意两节点之间的最短路, 最多可经过节点 $1、2\dots n$ 到达, 因此当迭代 $n$ 次时, 算法结束, 得到任意两点间的最短路及其距离.如本例题中, 节点 $1,6$ 之间的最短路为 $1-2-4-6$, 距离为 $9$; 节点 $3,4$ 之间的最短路为 $3-5-4$, 距离为 $3$; 节点 $6,4$ 之间的最短路为 $6-4$, 距离为 $3$ , 等等.

$${\mathrm{A}}_6=\left[\begin{array}{cccccc}0& 4& 6& 6_{124}& 5_{125}& 9_{1246}\\ 4& 0& 2& 2& 1& 5_{246}\\ 6& 2& 0& 3_{354}& 2& 6_{3546}\\ 6_{421}& 2& 3_{453}& 0& 1& 3\\ 5_{521}& 1& 2& 1& 0& 4_{546}\\ 9_{6421}& 5_{642}& 6_{6453}& 3& 4_{645}& 0\end{array}\right],R_6=\left[\begin{array}{cccccc}0& 0& 0& 2& 2& 4\\ 0& 0& 0& 0& 0& 4\\ 0& 0& 0& 5& 0& 5\\ 2& 0& 5& 0& 0& 0\\ 2& 0& 0& 0& 0& 4\\ 4& 4& 5& 0& 4& 0\end{array}\right]$$

Python 实现

import numpy as np
def floyd(graph):
    m = len(graph)
    dis = graph
    path = np.zeros((m, m))  #路由矩阵初始化
    for k in range(m):
        for i in range(m):
            for j in range(m):
                if dis[i][k] + dis[k][j] < dis[i][j]:
                    dis[i][j] = dis[i][k] + dis[k][j]
                    path[i][j] = k
    return dis, path
    # dis 为各顶点的最短距离矩阵
    # path 为路由矩阵