networkx基础使用
1. 前言
networkx支持创建简单无向图、有向图和多重图;内置许多标准的图论算法,节点可为任意数据。
Graph分类
- Graph:指无向图(undirected Graph),即忽略了两节点间边的方向。
- DiGraph:指有向图(directed Graph),即考虑了边的有向性。
- MultiGraph:指多重无向图,即两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联。
- MultiDiGraph:多重图的有向图版本。
import networkx as nx
G = nx.Graph() # 创建无向图
G = nx.DiGraph() # 创建有向图
G = nx.MultiGraph() # 创建多重无向图
G = nx.MultiDigraph() # 创建多重有向图
G.clear() #清空图
2.基本操作
2.1 添加节点
G = nx.Graph() # 实例化一个无向图
G.add_node('a') #添加一个节点
G.add_nodes_from(['b','c','d','e']) #添加 一群点
nx.draw(G, with_labels=True, node_color='g', edge_color='red', node_size=400, alpha=0.5)
# 结点绿色,边红色,结点大小400,透明度50%
# 由于没有添加边,所以图中没有显示边
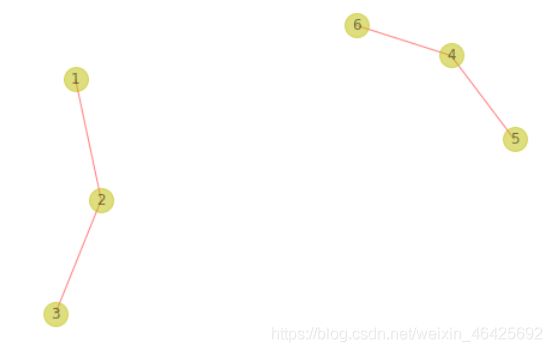
2.2 添加边
F = nx.Graph() # 创建无向图实例
F.add_edge(4,5) #一次添加一条边,由 6 到 7
#等价于
#e=(4,5) #e是一个元组
#F.add_edge(*e) # *是python中序列解包过程
F.add_edges_from([(1,2),(2,3),(4,6)]) #通过添加list来添加多条边
nx.draw(F, with_labels=True, node_color='y', edge_color='red', node_size=400, alpha=0.5)
打印所有边和结点
print('图中所有的边', F.edges())
print('图中边的个数', F.number_of_edges())
>>>>>>>>>>
图中所有的边 [(4, 5), (4, 6), (1, 2), (2, 3)]
图中边的个数 4
2.3 一次性画线性连接的无向图
H = nx.path_graph(10) # 6 个结点 线性连接 无向图
nx.draw(H, with_labels=True, edge_color='b', node_color='m', node_size=1000)
2.4 删除结点
#删除节点
G.remove_node("a") #删除指定节点
G.remove_nodes_from(['b','c']) #删除一群节点
nx.draw(G, with_labels=True, node_color='g', edge_color='red', node_size=400, alpha=0.5)
2.5 删除边
F.remove_edge(1,2) # 删除一条边
F.remove_edges_from([(4,6), (2,3)]) # 删除多条边
nx.draw(F, with_labels=True, node_color='y', edge_color='red', node_size=400, alpha=0.5)
2.6 图之间的转化
#有向图转化成无向图
G = D.to_undirected() # D 是有向图,G 是无向图
#或者
G =nx.Graph(D)
#无向图转化成有向图
D = G.to_directed() # G 是无向图,D是 有向图
#或者
D = nx.DiGraph(G)
3. 经典图论算法
函数调用:
- dijkstra_path(G, source, target, weight=‘weight’) ——求最短带权路径
- dijkstra_path_length(G, source, target, weight=‘weight’) ——求最短最短带权路径下的带权距离
- 示例
import networkx as nx
import pylab
import numpy as np
#自定义网络
row=np.array([0,0,0,1,2,3,6])
col=np.array([1,2,3,4,5,6,7])
value=np.array([10,2,1,8,1,3,5])
print('生成一个空的有向图')
G=nx.DiGraph() # 实例化有向图
print('为这个网络添加节点...')
for i in range(0,np.size(col)+1):
G.add_node(i) #一个一个的添加结点
print('在网络中添加带权中的边...')
for i in range(np.size(row)):
G.add_weighted_edges_from([(row[i],col[i],value[i])]) # 格式(结点1,结点2,权重)
G.add_weighted_edges_from([(row[i],col[6- i],value[i])])
print('给网路设置布局...')
pos=nx.shell_layout(G)
print('画出网络图像:')
nx.draw(G,pos,with_labels=True, node_color='g', edge_color='red', node_size=400, alpha=0.5 )
pylab.title('Self_Define Net',fontsize=15)
pylab.show()
'''
Shortest Path with dijkstra_path
'''
print('dijkstra方法寻找最短路径:')
path=nx.dijkstra_path(G, source=0, target=7)
print('节点0到7的路径:', path)
print('dijkstra方法寻找最短距离:')
distance=nx.dijkstra_path_length(G, source=0, target=7)
print('节点0到7的距离为:', distance)
打印结果

可以看到由 0 ——> 7 的最短路径不是[0,7]而是[0,6,7],这是因为 0 --> 7 的权重是 10,而[0,6,7] 的权重之和,也就是最短距离 是 7,所以输出是[0,6,7]