碰撞检测技术介绍

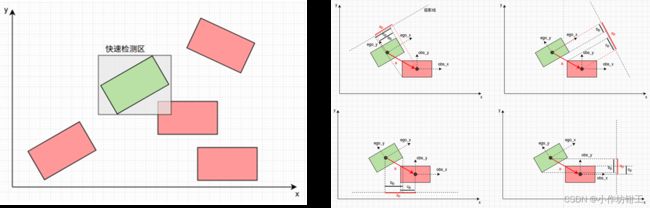
自动驾驶决策规划模块中会经常使用到碰撞检测计算分析Ego vehicle行为的安全性，并且可以用在planning计算的多个方面。例如下左图中的校验轨迹的安全性，下中图中计算路径的安全走廊，下右图中计算速度规划的ST图等等，虽然碰撞检测在planning中是一个小算法模块，但是却至关重要。

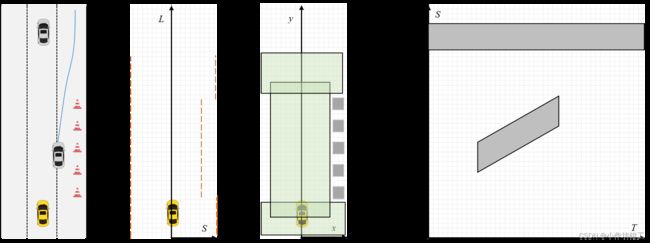
本文将对常用的碰撞检测算法进行介绍，并简要的进行benchmark。在planning中一般将主车以及障碍物处理为凸多边形(Polygon/Box)，因此碰撞检测多是检测两个Polygon是否重叠，但是为了不失一般性，本文也将介绍Polygon和Point的位置关系计算方法，因为在两个Polygon的位置关系计算中可能会用到。
本文介绍的碰撞检测方法有：

• Box和Point的碰撞检测：
  • OpenCV方法；
  • 射线法；
  • 轮廓六分圆法；
• Box和Box的碰撞检测：
  • OpenCV方法；
  • SAT（分离轴定理）；
  • GJK；

1. Box和Point的碰撞检测

1.1 OpenCV

此方法使用了OpenCV开源库中的图像处理的方法，可以简要分为以下计算步骤：

• 根据碰撞检测环境范围(矩形)，建立两个cv::Mat数据；
• 将ADC位置或者轨迹车辆投影转化到cv::Mat中，被ADC占据位置数据设置为1(非零)，其他为0；
• 将障碍物投影转化到cv::Mat中，被据位置数据设置为1 (非零) ，其他为0；
• 两个cv::Mat进行求与操作，得到的cv::Mat中数据如果有非0数据，则发生碰撞；

1.2 射线法

判断一个点是否在多边形内，我们可以从该点引出一条水平射线（任意射线都可，但水平便于计算），观察射线与多变形的交点个数，如果交点个数为奇数，则该点在多边形内，如果为偶数则在多边形外。如下左图所示，判断点P和多边形的关系，从点P得到一个水平向右的射线，通过多边形的每两个相邻顶点可以得到边的直线方程，例如$P_1{P}_2$，有$y_0$可以计算得到点B的坐标，就可以判断射线是否与$P_1{P}_2$相交了。此方法对多边形的凸凹性没有要求，但是如果点P在多边形边上或者顶点需要特殊处理。

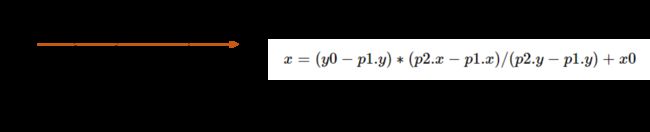
struct Point{
  double x, y;
};
bool IsInPolygon(Point p,Point *ptPolygon,int ncount) {
  int ncross = 0;
  for (int i = 0; i < ncount; i++) {
    Point p1 = ptPolygon[i];
    Point p2 = ptPolygon[(i + 1) % ncount]; //相邻两条边p1,p2
    if (p1.y == p2.y)  continue;
    if (p.y < min(p1.y, p2.y))  continue;
    if (p.y >= max(p1.y, p2.y))  continue;
    double x = (p.y - p1.y)*(p2.x - p1.x) / (p2.y - p1.y) + p1.x;
    if (x > p.x)  ncross++; //只统计单边交点
  }
  return(ncross % 2 == 1);
}

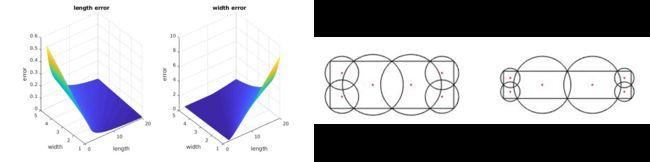
1.3 轮廓六分圆法

此方法是将矩形的碰撞检测转化为圆之间的碰撞检测，通过两个圆的半径和圆心之间的距离判断两个圆是否重叠。给定车辆矩形轮廓，该算法首先计算矩形轮廓的外接圆，然后将整个矩形区域分解成与四个角点对齐的同等大小的正方形，轮廓矩形区域剩下的部分再进一步分解成等大小的小矩形，最后计算每一个小矩形或正方形的外接圆[1]。


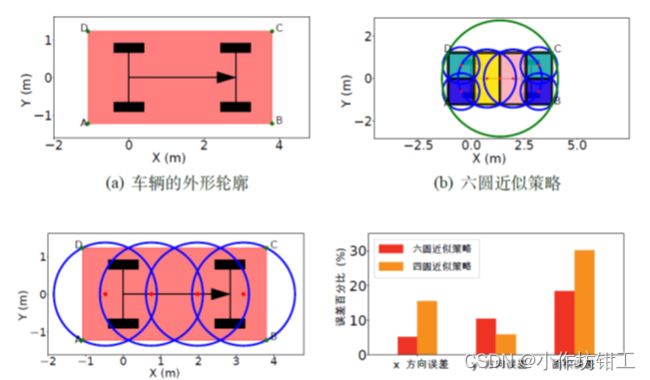
此方法的计算精度损失较大，并且和矩形的长宽比例有关，可以看到当矩形为正方形时误差最小。此外此方法可以使用更多的圆计算矩形，并且更改圆的覆盖方法，但并不能彻底消除误差，同时更多的圆会增大计算时间。

• 矩形长度对横向误差影响较大；
• 矩形宽度对纵向误差影响较大；
  

2. Box和Box的碰撞检测

2.1 OpenCV方法

和上述方法一致。

2.2 SAT

如果凸多边形在某个轴上的投影不重叠，则两个凸多边形不相交。需要对所有的轴(每个边的法向量)进行投影，存在一个轴上的投影不相交，则两个凸多边形不相交。如果所有轴上的投影都相交，则多边形相交。
见之前的文章：Planning-碰撞检测之分离轴定理(SAT)
此外，SAT也可以用来计算Box和Point的位置关系。

2.3 GJK

$GJK$是基于$Minkowski$ $Sum$概念上的，即形状1的所有点和形状2的所有点之和。
$A+B=\{a+b|a\in A,b\in B\}$
如果$shapeA$和$B$是凸的，则它们的和也是凸的
相应的可以定义它们的差运算：
$A-B=\{a-b|a\in A,b\in B\}$
如果两个形状重叠，进行$Minkowski$ $Sum$后的形状包含原点。$Minkowski$$Sum$的运算是$shape$ $A$的每个顶点和$shape$ $B$的所有顶点求和（或求差）。所得到点的外包络即是运算所得形状。
见之前的文章：Planning-碰撞检测之GJK

3. Benchmark

通过Benchmark分析，这里给出定性的计算结果：

3.1 Box和Point的碰撞检测

• 性能：轮廓六分圆 >> 射线法 >> OpenCV；
• 精度：射线法 >> OpenCV > 轮廓六分圆；

3.2 Box和Box的碰撞检测

• 性能：GJK > SAT >> OpenCV；
• 精度：GJK = SAT >> OpenCV；
  当Polygon为四边形时，GJK和SAT的计算时间基本相等，但是随着Polygon边数的增多，GJK的性能优越性就凸显出来了。
  具体代码实现以及Benchmark可见：collision_detection

4. 其他算法

4.1 Apollo中碰撞检测算法

Apollo的planning模块中的碰撞检测算法使用的有SAT和射线法两种。

4.1.1 SAT

• 车辆作为一个3D物体，降维到(x,y)二维上，使用长方形bounding box简化代替；
• 对bounding box进行AABB快速检测；
• 对bounding box进行OBB快速检测：应用SAT，用到坐标系旋转计算投影；
  

4.1.2 射线法

由于Box(矩形)是凸的，因此，当两个Box发生碰撞时，必然首先发生在角点处，即一个box的角点进入另一个box的内部。Apollo中使用射线法判断一个点是否在一个多边形内部。

for (const auto& point : ADCpoints) {
  for (const auto& obstacle : obstacls) {
    if (obstacle.IsPointIn(point)) {
      return ture;
    }
  }
}
// 正确的做法应该同时进行：
for (const auto& obstacle : obstacls) {
  for (const auto& point : obstacle.points) {
    if (ADC.IsPointIn(point)) {
      return ture;
    }
  }
}

bool Polygon2d::IsPointIn(const Vec2d &point) const {
    if (IsPointOnBoundary(point)) { return true; }
    int j = num_points_ - 1;
    int c = 0;
    for (int i = 0; i < num_points_; ++i) {
        if ((points_[i].y() > point.y()) != (points_[j].y() > point.y())) {
            const double side = CrossProd(point, points_[i], points_[j]);
            if (points_[i].y() < points_[j].y() ? side > 0.0 : side < 0.0) {
                ++c;
            }
        }
     j = i;
    }
    return c & 1;
}

上述Box的碰撞检测是根据矩形特点对SAT方法的简化，Polygon是任意多边形，则不再适用上述方法。由于Polygon是凸的，两个Polygon的最短距离必然发生在Polygon A的某个点和Polygon B的某个点，或者Polygon A的某个点和Polygon B的某条边之间。因此，判断两个Polygon是否有重合，转化为计算两个Polygon的最短距离是否小于等于0。其中用到了射线法判断点是否在Polygon内和点到线段的距离。

4.2 开源算法

• OpenGJK(GJK based Signed Volumes): https://github.com/MattiaMontanari/openGJK
• Bullet: https://github.com/bulletphysics/bullet3
• FCL: https://github.com/flexible-collision-library/fcl
• Box2D: https://github.com/erincatto/box2d

5. 参考文献：

[1] 张玉.自动驾驶车辆混合运动规划研究[D].北京理工大学,2018.