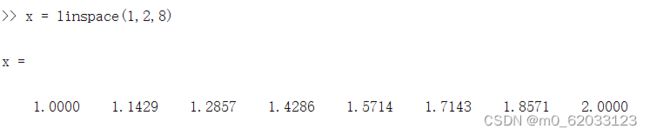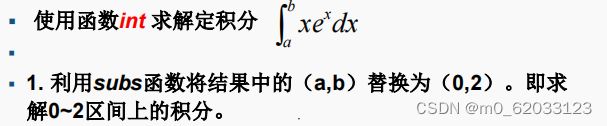刘卫国《MATLAB程序设计与应用》个人笔记

第一章：初识MATLAB

1.1MATLAB是什么？

 ①矩阵实验室MATrix LABoratory的英文缩写
 ②交互式系统
 ③程序设计语言
 ④多个应用领域工具箱的集合

注意：

• 通常，我们执行程序或调用函数，都需要程序或函数文件需在当前路径下，否则会提示错误。
• Matlab中 变量不需定义，可直接赋值使用，但是注意未经赋值不能直接使用

1.2MATLAB的搜索路径

Workspace中的变量->内部函数->当前目录下的程序文件->MATLAB搜索路径中的其它目录下的m文件->提示错误

1.3MATLAB帮助命令

①help、doc命令：
格式：帮助命令 函数名或者主题名
②lookfor命令：
help关键字之搜索出那些关键字完全匹配的结果，lookfor命令对搜索范围内的m文件关键字进行搜索，条件比较宽松 。
lookfor命令只对M文件的第一行进行关键字搜索。若在lookfor命令加上-all选项，则可对M文件进行全文搜索。

1.4指令窗常用的控制指令

指令	含义
clf	清除图形窗口
clc	清除指令窗中显示的内容
clear	清除MATLAB工作空间中保存的变量
edit	打开m文件编辑器

第二章：MATLAB数据及其运算（包括第三章）

2.1变量及其操作

2.1.1变量的命名规则：

      ①首先必须以字母开头
 	  ②后接数字、字母或下划线
 	  ③对大小写敏感
 	  *注意：应避免对预定义变量重新赋值，不要使用matlab的内部函数名作为变量名。*

2.1.2常用的预定义变量

预定义变量	含义
ans	计算结果的默认赋值变量
i，j	虚数单位
inf/Inf	无穷大（如1/0的结果）
NaN、nan	非数（如inf/inf，0/0）的结果
nargin	函数输入参数个数
nargout	函数输出参数个数

（应避免对这些变量重新赋值，也不要使用matlab的内部函数名作为变量名。）

2.1.3变量的管理

	->查看变量:who/whos:直接在工作空间中查看
	->删除变量：clear/clear all，例：clear x，y（删除x，y）
	->存储save（默认为mat文件），例：save mydata.mat
	->导入数据load，例：load mydata

2.2 MATLAB矩阵的建立和表示

2.2.1 矩阵的表示

      ①矩阵的建立：直接输入法、函数法(调用函数）
 	  ②矩阵的引用：双下标、单下标、逻辑1
 	  ③注意几个不同类型括号的不同应用目的和适用场合：中括号[ ], 圆括号( )，花括号{ }

2.2.2 创建矩阵

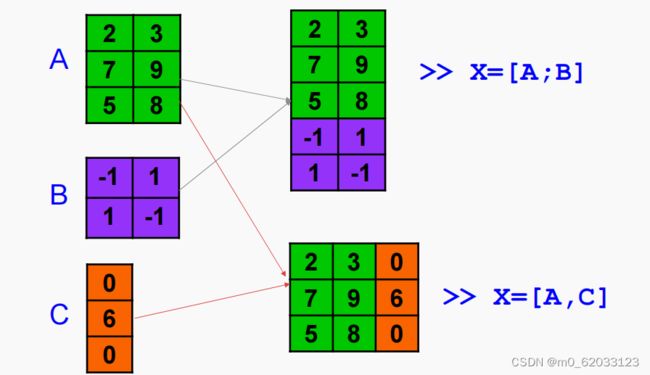
1、直接输入法
-中括号[]。
-按行顺序输入。
-每一行的元素与元素的分割使用空格或者逗号。
-行与行的分割使用回车或者分号。
2、函数法（常用的函数）

函数	功能
zeros	产生全0矩阵
ones	产生全1矩阵（幺矩阵）
eye	产生单位矩阵（对角线全为1）
rand	产生0-1之间的随机数矩阵
randn	产生均值为0，方差为1的标准正态分布的随机矩阵

举例：
产生两行三列的幺矩阵


产生3行3列的单位矩阵

3、产生行向量（等间距）
①使用linspace

%生成 n 个点。这些点的间距为 (b-a)/(n-1)。
x = linspace(a,b,n)

4、拼接数组

2.2.3 通过函数查询矩阵的规模

->size
·矩阵大小

->length
·返回数组最大维数的长度

->ndims
·返回数组的维数

->numel
·返回数组元素个数

2.2.4矩阵（或数组）元素的引用（访问）

1、单下标

2、单下标和双下标的转换
·单转双：

[I,J] = ind2sub(matrixSize,IND)

·双转单

linearInd = sub2ind(matrixSize, rowSub, colSub)

3、总结如下

访问多行、多列的元素：（表中I，J视为向量；i，j视为标量）

矩阵元素的访问	说明
A（I，J）	访问由向量I，J指定的矩阵A中的元素
A（i，：）	访问矩阵A中第i行的所有元素
A（：，j）	访问矩阵A中第j列的所有元素
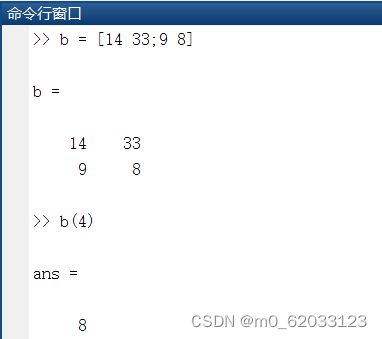
A（L）	访问由向量L指定的矩阵A的元素，向量L中的元素为矩阵元素的单下标值

注意这里：冒号（：）------表示所有
end----------表示最后
4、巧用逻辑1标志进行访问
举例：
1、产生5阶随机方阵A，其元素为[10,90]区间的随机整数，然后输出A中能被3整除的元素。学习用：函数：rand(产生0~1的随机数)取整：round、fix、floor、ceil 取余：rem

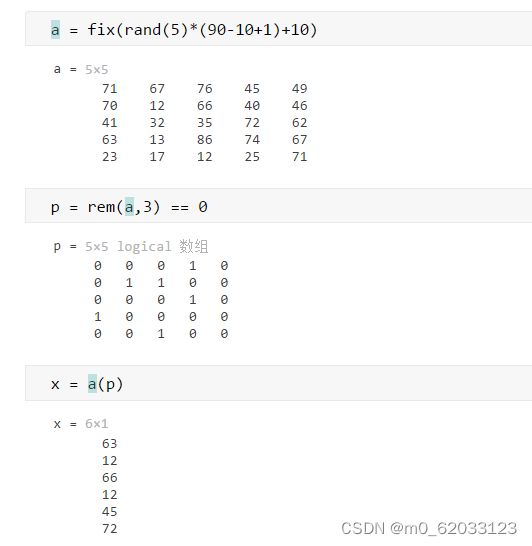
2、、建立矩阵A = [4,15,-45,10,6;56,0,17,-45,0]然后找出A中值在区间[10，20] 的这个范围内元素的位置。学习使用：函数find
求解：

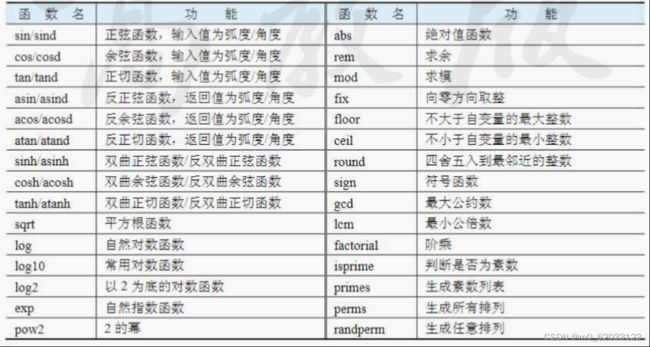
2.3MATLAB常用的内部函数

1、常用的函数如下

2.4 MATLAB运算

1、算术运算
·+，-
·矩阵运算：

符合	功能
*	乘
\	左除
/	右除
^	幂

注意左除和右除的区别

·数组元素间的运算（数组运算或点运算，进行每个元素间的操作）：

符合	功能
.*	点乘
.\	点左除
./	点右除
.^	点幂

->实例：
求解线性方程组：

解答如下：
2、关系运算和逻辑运算
->关系运算
·<,<=,>,>=,==,~=
->逻辑运算
·&（and（a，b）
·| (or （a，b）
·~（not（a）
逻辑运算符表
（不是类似进行比较那样是否相等，而是逻辑运算）

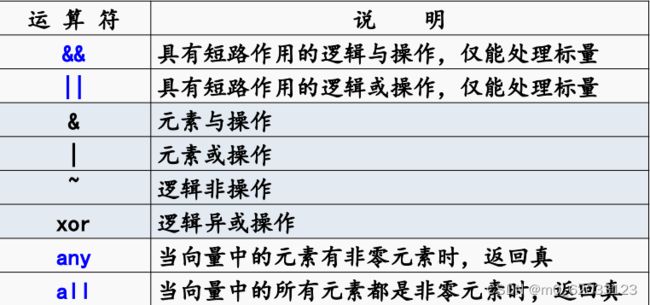
注：标量就是单个元素（&&，||只能处理单个元素）
例：

3、Matlab的运算符的优先级
高--------------------------------------------->低
算术运算 关系运算 逻辑运算

2.5结构数据和单元数据

·特点：均可将不同的相关数据集成到一个单元的变量中

2.5.1结构数据

·将一组类型不同而逻辑上相关的数据组成一个有机的整体。
->结构1数据允许一个名字绑定多个变量
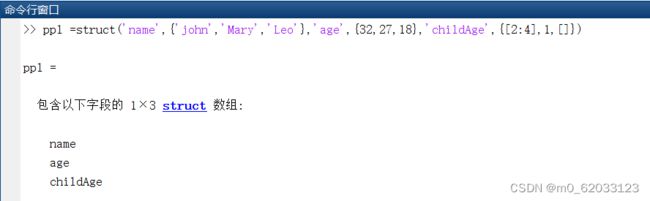
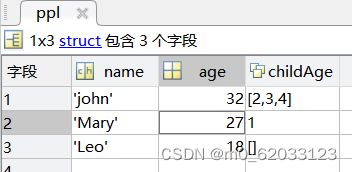
->建立结构数组

s.name =  'Jack Bauer’;
s.scores= [95 98 67];
s.year = 'G3';

->建立一个结构数组

结果：

例题：

2.5.2单元数据

·单元数组：其形式看上去像一个数组，但是其元素不必是同一类型。

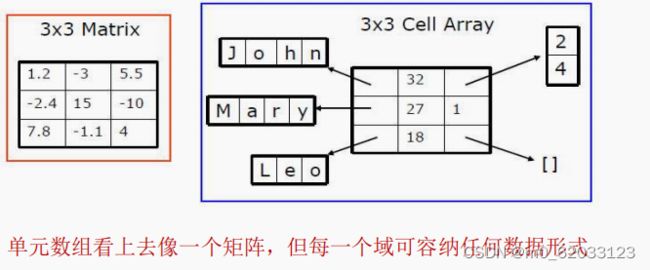
->单元数组的建立
·建立一个指定大小的单元数组

%建立一个3行4列的单元数组（空）
a = cell(3,4);
%将单元数组的元素用大括号括起来{}
c = {'hello word',[1 5 6 2],rand(3,2)};%c是一个1行3列的单元数组

结果：

第四章：MATLAB程序流程控制

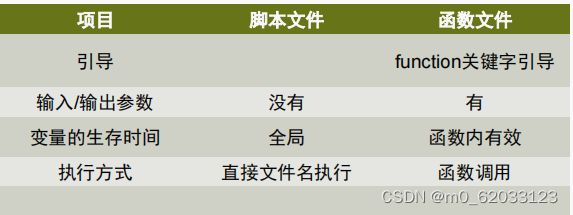
4.1脚本文件和函数文件

·脚本文件（也叫命令文件）
-是由一系列matlab可执行程序的语句组成的纯文本格式的m文件。
-不接受输入参数和输出参数。
-调用方法：在matlab命令窗口直接输入脚本文件的文件名
·函数文件
-由function语句引导的m文件
-调用格式：[输出实参表] = 函数名（输入实参表）
·两者区别
注意：函数名与所存的m文件名应同名； ？（最好保持一致）当两者不同时，MATLAB将忽略函数名，调用时使用函数文件名。

4.2程序控制结构

4.2.1选择结构

if语句

if cond
	commands
end

else语句

if cond 
	commands1
else
	commands2
end

elseif语句

if cond1
	commands1
elseif coond2
	commands2
else
	commands3
end

switch语句

switch expr
	case value_1
		commands1
	case value_2
		commands2
		.......
	case value_k
		commandsk
	otherwise
		commands
end

注意：
·switch子句其后母的表达式的结果应为一个标量或一个字符串；
·case子句其后通常为一个标量或一个字符串，或者一个单元数据。如果为一个单元数据，则expr的值与匹配该单元中的某一个元素时，就执行相应语句。
·otherwise是可选的。
·如果需要针对多个条件而使用同一个case分支的时候，需要使用单元数据与之配合。
举例：
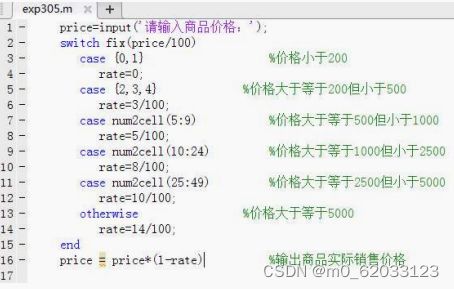
某商场对顾客所购买的商品实行打折销售，标准如下(商品价格用price来表示)： – price<200 没有折扣 – 200≤price<500 3%折扣 – 500≤price<1000 5%折扣 – 1000≤price<2500 8%折扣2500≤price<5000 10%折扣 – 5000≤price 14%折扣 – 输入所售商品的价格，求其实际销售价格。
解答：
（num2cell是将数据矩阵转换为单元矩阵）

4.2.2循环结构

1、关于if语句的补充说明
·当if 后面的条件表达式是仅对标量进行操作时，其使用规
则与C语言类似。
·当if后面的条件表达式是对矩阵进行操作的时候，如果矩
阵非空，且不含0元素，则条件成立，否则视为条件不成
立。
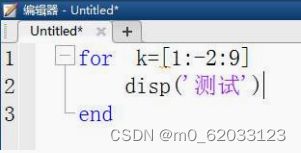
2、在for循环语句中，不仅可以：① 使用行向量进行循环迭代的处理；② 也可以使用矩阵作为循环次数的控制变量
循环的索引值将直接使用矩阵的每一列，循环的次
数为矩阵的列数，参见下列。

3、while循环结构的关系表达式可以是某个数据变量或者常量，这时，将按照非零为逻辑真进行相应的操作。另外当while语句后为矩阵时，与if类似，当A非空，且不含0元素，则视为逻辑真。否则，视为逻辑假。参见下列。

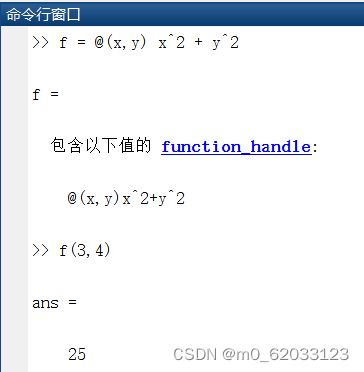
4.3匿名函数

1、格式：函数句柄变量（相当于函数别名） = @（匿名函数输入参数）匿名函数表达式

第五章：MATLAB绘图

5.1设置曲线样式

·曲线的颜色，标记符号，线型可以通过在函数中增加字串参数来改变。

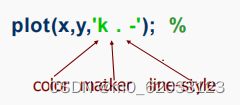
5.2绘制多条曲线

例：
·方法一：利用plot函数

plot(x,[y1,y2])
%或者
plot(x,y1,x,y2)

·方法二：利用图形保持命令hold

plot(x,y1);
hold on 
plot(x,y2);
hold off

5.3图形的标注及坐标控制

5.3.1图形标注

· title(图形标题)
· xlabel(x轴说明)
·ylabel(y轴说明)
·text(x,y,图形说明）
·legend（图例1，图例2，…)

5.3.2坐标控制

1、 axis函数的其他常见用法
axis square：长宽比例为1，产生正方形坐标系 。
axis equal ： 纵、横坐标采用等长刻度。
axis auto：使用默认设置。
axis off ：取消坐标轴。
axis on ： 显示坐标轴。
grid on：显示网格。
xlim([-n,n]):控制x范围从-n到n。
ylim([-n,n]):控制y范围从-n到n。
axis（[-n n -m m]):控制x范围从-n到n，y范围从-m到m。
2、绘图要点

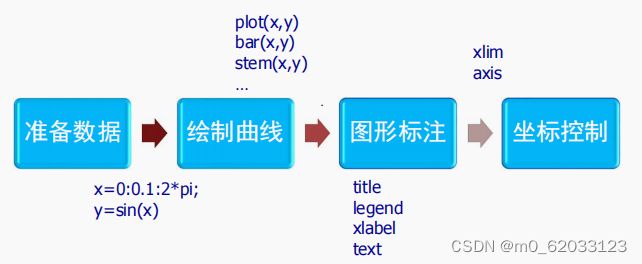
3、更多类型图形的绘制函数
①条形图（垂直/水平）：bar（垂直），barh（水平）。
②梯形图/杆图：stairs（梯形），stem（杆图）。
③饼图：pie。
④极坐标绘图采用：polar
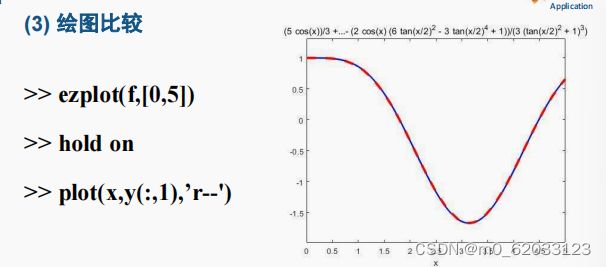
⑤隐函数绘图：ezplot
– 函数f=f(x)
– 函数f=f(x,y),f(x,y)=0
– 参数方程x=x(t),y=y(t)
例：

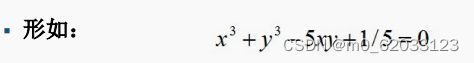
解答：

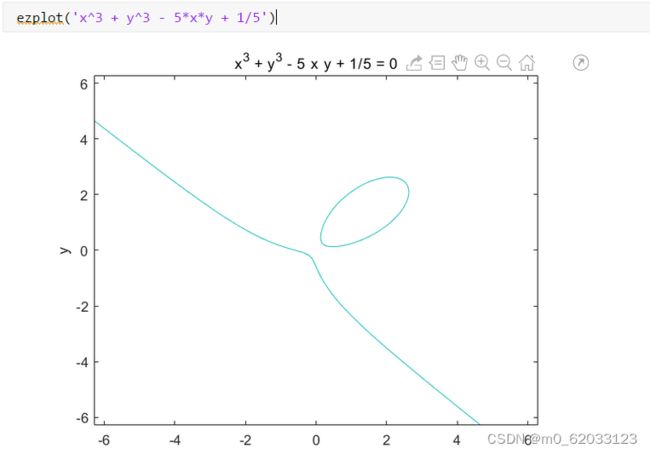
第六章 MATLAB数据分析与多项式计算

6.1数据统计分析

1、输入数据为二维
按列操作
– max(B,[],1)
– std(B,0,1)
– mean(B,1)

按行操作
-max（B,[],2)
-std(B,0,2)
-mean(B,2)

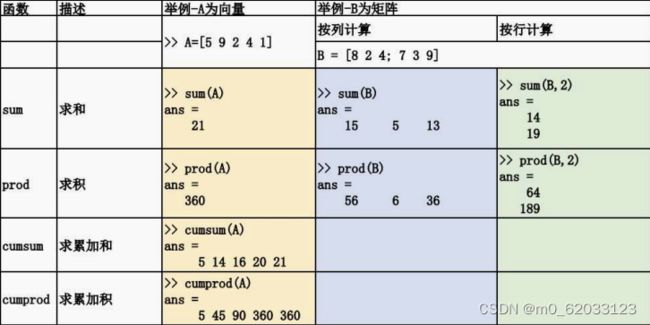
2、函数使用总结如下

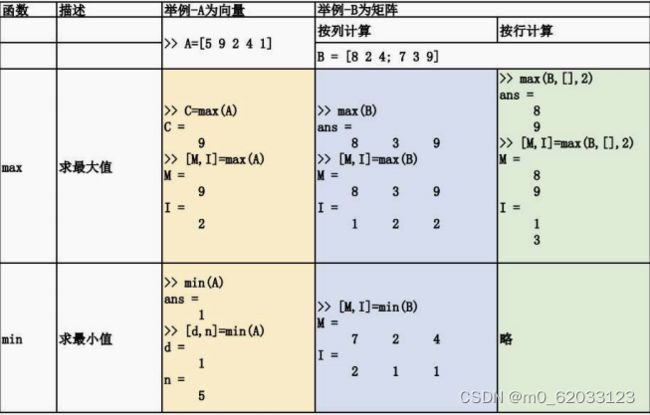
（个别说明）

%min和max类似
[M,I] = max(B)%返回的是每一列的最大值以及是该列的第几个。
[M,I] = max(B,[],2)%返回的是每一行的最大值以及是该行的第几个。

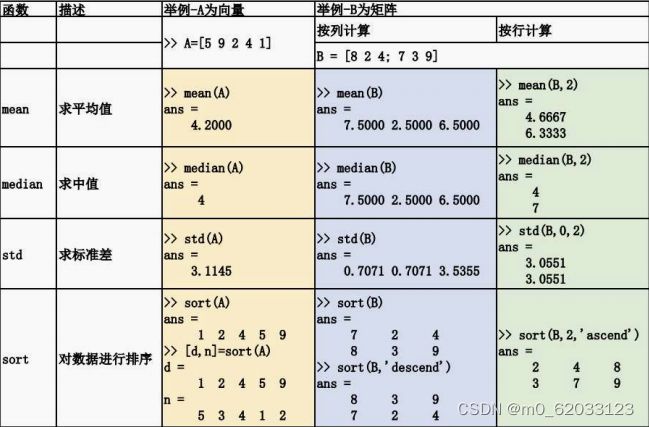
（附加）思考内容
1、仅使用第一种格式，对矩阵按行求最大元素？
解答：max（B')
2、只调用一次max函数就能求得整个矩阵的最大值？
解答：max(B(:))

6.2多项式的计算

6.2.1多项式的表示

·在MATLAB中，n次多项式用一个长度为n+1的行向量表示，缺少的幂次项系数为0。
·如果n次多项式表示为：

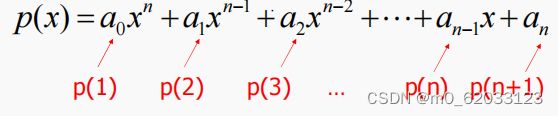
则在MATLAB中表示为向量形式：

举例：

6.3多项式四则运算和导数

6.3.1多项式四则运算

1、多项式的四则运算： + - （加减）
·具有相同的阶次；
·如果阶次不同，低阶的多项式必须用零填补至高阶多项式的阶次。
2、多项式的乘法运算（卷积）

%求多项式p1，p2的乘积
-conv(p1,p2)

3、多项式除法(去卷积)

%计算多项式p1除以p2，结果q为商，r为余式
%deconv是conv的逆函数，即p1=conv(p2,q)+r
[q,r] = deconv(p1,p2)

6.3.2多项式的导数

->polyder语法

%求多项式p得导数
p = polyder(p)
%求多项式p*q的导数
p = polyder（p,q)
%求多项式p/q的导数,导数的分子存入p，分母存入q
[p,q] = polyder(P,Q)

举例：

6.3.3多项式求值

——polyval(代数多项式求值）
语法：polyval(p,x)（注意与polyvalm区别）
举例：

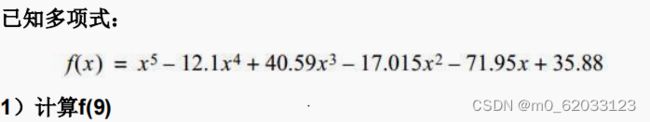
解答：

6.3.4多项式求根

——roots
语法：x = root§
(若已知多项式的全部根，则可用poly函数建立多项式。语法 p = poly(x))
举例：

解答：

6.4数据插值

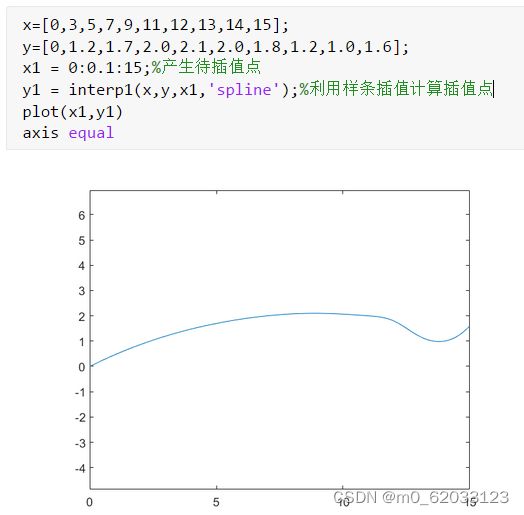
6.4.1一维插值

——interp1()
语法：Y = interp1(x,y,x1,method)
–该语句将根据x、 y的值，计算函数在x1处的值。
–其中， x ,y是两个等长的已知向量，分别表示采样点和采样值。 x1是一个向量或标量，表示要插值的点.
-method参数指定插值方法，常用的方法如下

参数	说明
linear	线性插值，默认方法
nearest	最近点插值
pchip	分段3次埃尔米特插值
spline	3次样条插值

（了解内容）

举例：

6.4.2二维数据插值

——interp2
语法：
z1 = interp2(x,y,z,x1,y1,method)
-其中， x、 y是两个向量，表示两个参数的采样点， z是采样点对应的函数值。
-x1、 y1是两个标量或向量，表示要插值的点。

6.5数据拟合

——ployfit（功能为求得最小二乘拟合多项式系数）
语法：p = polyfit(x,y,m)
举例：
测得铜导线在温度为Ti的电阻Ri如下表，求电阻R和温度T的关系。

解答：

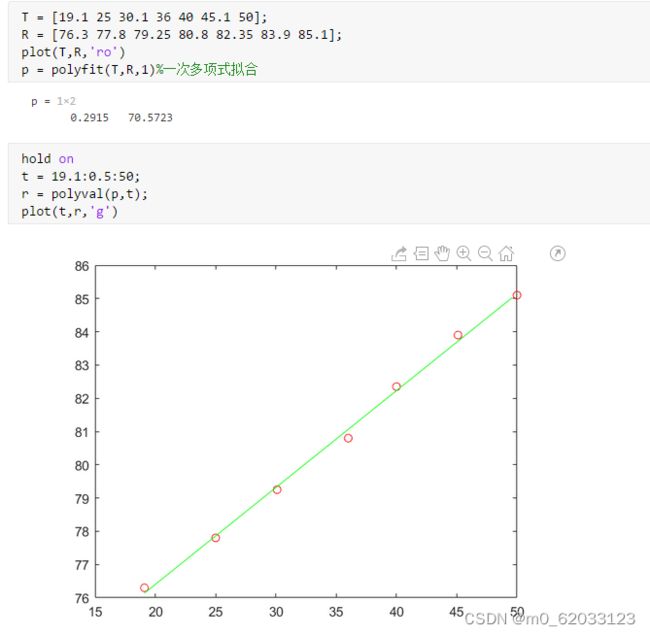
第七章 MATLAB数值微分与积分

7.1diff计算差分

1、语法：
y = diif(x)
y = diff(x,n)
y = diff(x,n,dim)
注意
diff函数计算的是向量元素间的（向前）差分，故差分向量元素的格式比原向量少了一个。同样，对于矩阵来说，差分后的矩阵比原矩阵少了一行或一列。另外，计算差分后，可以用f(x)在某点处的差商作为其导数的近似值。
举例：

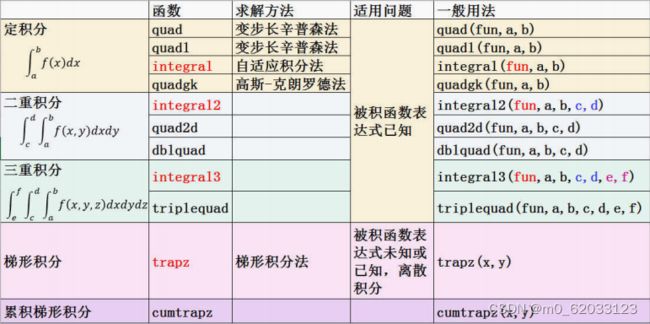
7.2求解积分函数

举例：
求定积分：

第八章 MATLAB方程数值求解

8.1线性方差求解

数值解法
• AX=B
• X=A\B（左除） 或 X=inv(A)*B（求逆）。

8.2非线性方差求解

1、所用到的函数

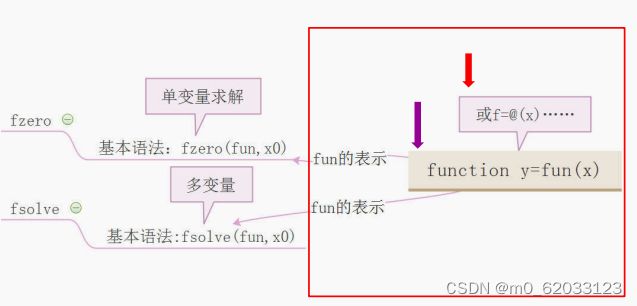
2、单变量非线性方差求解：fzero
·求解问题类型：f(x) = 0

3、求解函数实现方式
·函数文件：

%1为临近点，myfun为定义函数文件
fzero(@myfun,1)   

·匿名函数实现
举例·：
解答：

4、多变量非线性方差求解：fsolve(fun,x0)
·格式：x = fsolve(fun,x0)
-其中，x为返回的近似解，fun是待求根方差的函数表达式，x0是初值。
-也可以调用：x = fsolve(fun,x0,option)
·option用于设置优化工具箱的优化参数，可以调用optimset函数完成。
·利用fsolve求解上题：

举例：

解答方式一：函数文件

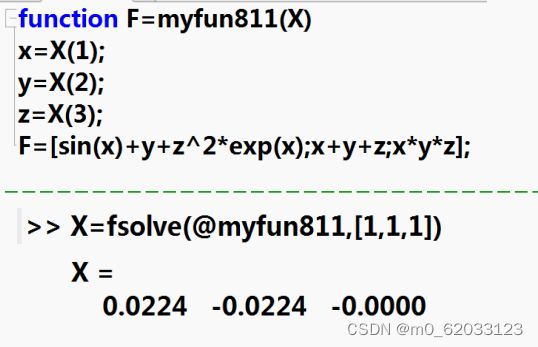
解答方式二：匿名函数

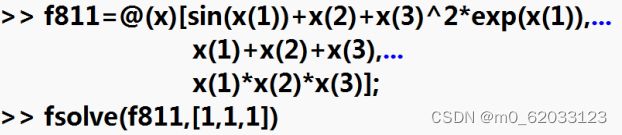
5、总结：

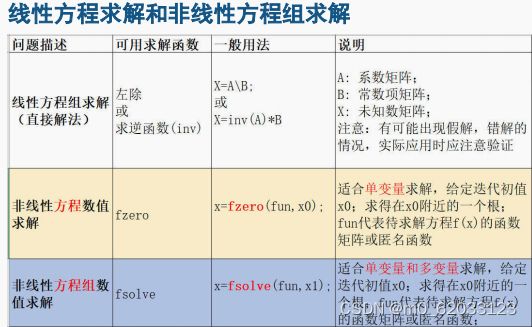
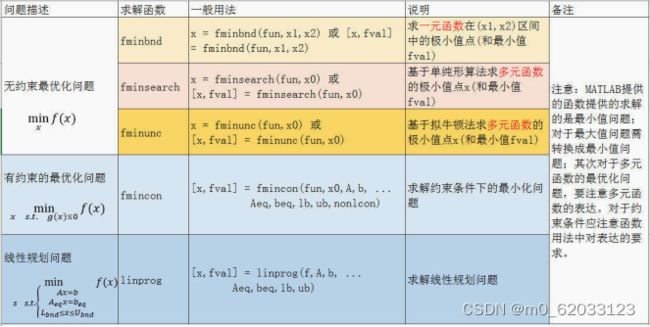
8.3最优化问题

8.3.1无约束最优化问题

· [x,fval] = fminbnd( fun , x1 , x2)
· [x,fval] = fminsearch( fun , x0)
· [x,fval] = fminunc( fun , x0)
– 其中，x表示极小值点，fval表示最小值，filename是定义的目标函数(匿名函数或函数文件形式)。 – 第一个函数的输入变量xl、x2分别表示被研究区间的左、右边界。 – 后两个函数的输入变量x0是一个向量，表示极值点的初值。 – 可以通过optimset函数来设置options，选择不同的参数。
举例：
解答方式一：函数文件

解答方式二：匿名函数

8.3.2有约束最优化问题

1、fmincon（非线性问题）
-有约束条件的多元函数的极小值求解
-调用格式如下：

各个参数对应不等式的约束形式：

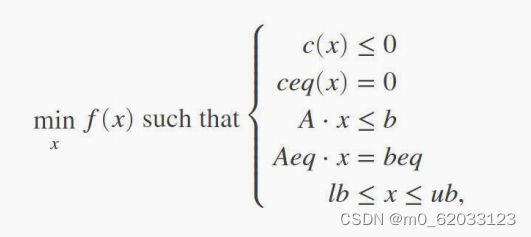
各种约束的表达：

举例：

约束条件的表示：

解答：

8.3.3线性规划问题求解

·linprog
-格式：[x,fval] = linprog(f,A,b,Aeq,beq,ib,ub)
举例讲解：

解答：

8.4总结

8.5常微分方程初值问题的数值解函数

• 一般格式

%格式[t,y] = solver_name(ODEfun,tspan,y0)，举例如下
[t,y] = ode45('myODE',[0,10],[1;0])

• 说明
  
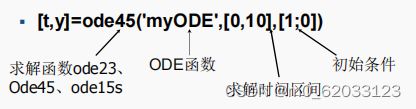
• 输入部分：
  -ODE函数文件（也可以用匿名函数）函数的输入通常为（t，y），返回值为dy/dt。
  -求解区间：2个元素向量指定初始和终止时间。
  -初始条件：表示每个ODE初始条件的向量，是ODE函数的第一个输入。
• 输出部分
  -t包含所有的间隔点
  -与t所对应的y值
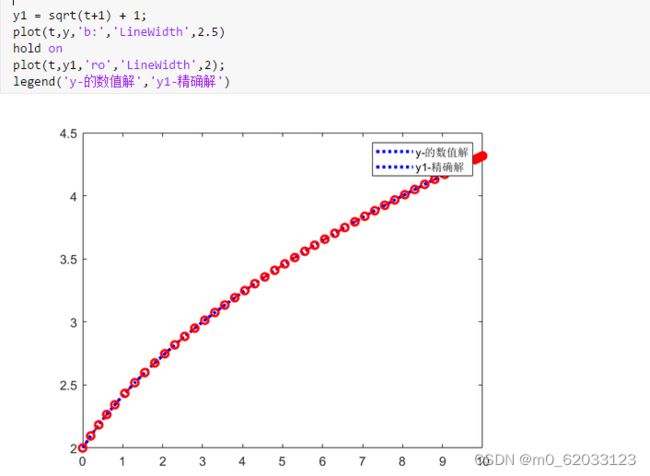
  举例：
  
  解答：
  定义函数文件
  
  与精确解比较
  

第九章 MATLAB符号计算

9.1 符号变量和符合表达式

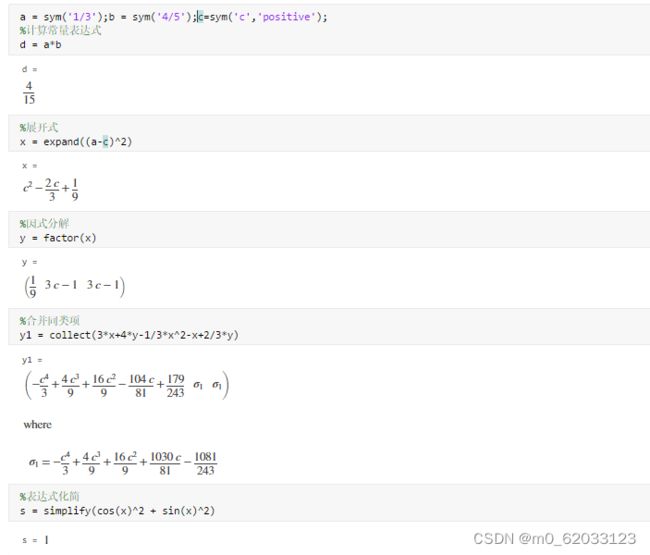
9.1.1符合常量和符合变量

• 使用sym建立符合常量或符合变量
  举例：
  
• 或者使用syms
  

9.2符号表达式的计算

9.2符号方程求解

• solve(s):求解符合表达式s的代数方程，求解变量为默认变量。
• solver(s,v):求解符合表达式s的代数方程，求解变量为v。
• solver([s1,s2…sn],[v1,v2…vn]):求解符合表达式s1,s2…sn组成的代数方程组，求解变量为v1,v2…vn。
  举例：
  解下列方程组：
  
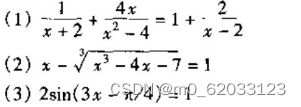
  解答：
  

9.3符号求解定积分

1、举例讲解

解答：

2、举例讲解：

解答：

9.4符号函数求导

• diff(f):系统按默认变量求符号表达式的一阶导数
• diff(f,v)：对f求一阶导数，自变量为v ·
• diff(f,n)：对f求n阶导数
• diff(f,v,n)：以v为自变量，求f的n阶导数
  注：f为符号表达式

9.5 符号常微分方程求解

• dsolve(eq,c,v)
• dsolve(eq1,eq2,…,eqn,…c1,…,cn,v1,…,vn)
  举例1：
  
  解答：
  
  举例2：
  求微分方程初值问题的符号解，并与数值解进行比较
  
  解答：
  符号解：
  
  数值解：
  
  绘图比较：