西瓜书第三章阅读笔记

本章节直接啃书的话，在公式的运算方面可能有一点难度。强烈推荐配合Datawhale的讲解视频配合使用，思路会更加清晰，也能更系统地建立思路。记得一键三联哈哈哈哈哈哈哈！（视频链接放在文章末尾啦~）

第三章 线性模型

1、机器学习三要素

• 模型 ：根据具体问题，确定假设空间
• 策略 ：根据评价标准，确定选取最优模型的策略（通常会产生一个“损失函数”）
• 求解算法 ：求解损失函数，确定最优模型

 关于具体机器学习算法的学习掌握均可从这三要素出发

2、基本形式

  示例 x=（x₁；x₂；. . . ；x_d)有d个属性描述，线性模型（linear model） 尝试学得一个通过属性线性组合来进行预测的函数，即$$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$$
  其向量形式为$$f(\mathbf{x})={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b(\mathbf{w}=(w_1;w_2;...;w_d))$$
  参数w和b通过学习确定后，模型即确定。

  线性模型优点与意义：

• 形式简单，易于建模
• 蕴含着机器学习中一些重要的基本思想
• 可在其基础上通过引入层级结构或高维映射以得到非线性模型（nolinear model）
• 有很好的可解释性（comprehensibility）

3、线性回归

3.1 模型

  给定数据集D={（x₁,y₁）,(x₂,y₂)，… ，（x_m,y_m）}，其中x_i=（x_i1；x_i2；… ；x_id）。“线性回归”（linear regression）试图学得一个线性模型来尽可能准确地预测实值输出标记，即$$f(x_i)={\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}+b,使得f({\mathbf{x}}_{\mathbf{i}})\approx y_i$$
  当属性个数为1时，即一元线性回归；属性个数多个时，即多元线性回归。

3.2 策略

  使用 均方误差（square loss） 来衡量f(x)与y之间的差别，采用让均方误差最小化的策略来选择模型。
$$均方误差E=\sum _{i=1}^m(y_i-f({\mathbf{x}}_{\mathbf{i}}){)}^2$$
$$E=\{\begin{array}{ll}{E}_{(w,b)}={\sum }_{i=1}^m(y_i-w{x}_i-b)& \text{ 一元线性回归}\\ E_{\hat{w}}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathbf{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})& \text{ 多元线性回归}\end{array}$$
  其中 $\hat{\mathbf{w}}=(\mathbf{w};b)$，具体细节可翻阅西瓜书。

  下图所示为分别使用最小二乘法和极大似然估计法来推导出线性回归模型的损失函数的过程。

3.3 求解算法

  求解参数使得误差最小化的过程，称为 “参数估计”（parameter estimation） 。

1.对于一元线性回归，将$E_{(w,b)}$分别对w和b求导，可得：
$$\frac{\partial E_{(w,b)}}{\partial w}=2\left(w\sum _{i=1}^m{x_i}^2-\sum _{i=1}^m(y_i-b)x_i\right)$$
$$\frac{\partial E_{(w,b)}}{\partial b}=2\left(mb-\sum _{i=1}^m(y_i-w{x}_i)\right)$$
  令一阶导数为零可得到w和b最优解的闭式解：
$$w=\frac{{\sum }_{i=1}^m{y}_i(x_i-\bar{x})}{{\sum }_{i=1}^m{x_i}^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}$$
$$b=\frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)$$
2.对于多元线性回归，将$E_{\hat{w}}$分别对w和b求导，可得：
$$\frac{\partial E_{\hat{w}}}{\partial \hat{w}}=2{\mathbf{X}}^{\mathbf{T}}(\mathbf{X}\hat{\omega }-\mathbf{y})$$
  在满足$\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$为满秩矩阵或正定矩阵时，令上式为0可得 $\hat{w}$ 的闭式解：
$${\hat{w}}^{\ast }=(\mathbf{X}{\mathbf{X}}^{\mathbf{T}}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$

补充：
  对数线性回归（log-linear regression）：
$$lny={\omega }^{\mathbf{T}}\mathbf{x}+b$$
  其实际上是在试图让$e^{{\omega }^{\mathbf{T}}\mathbf{x}+b}$逼近y，实质上已经是在求取输入空间到输出空间的非线性函数映射。
  更一般地，考虑单调可微函数$g(\cdot )$，令$y=g^{-1}({\omega }^{\mathbf{T}}\mathbf{x}+\mathbf{b})$，称其为广义线性模型（generalized linear model）

4、对数几率回归

4.1 模型

  在线性模型的基础上加上一个映射函数实现分类。
  在对数几率回归中使用的映射函数即对数几率函数（logistic function）—— $y=\frac{1}{1+e^{-z}}$，是一种“Sigmoid”函数，其图形如下所示：

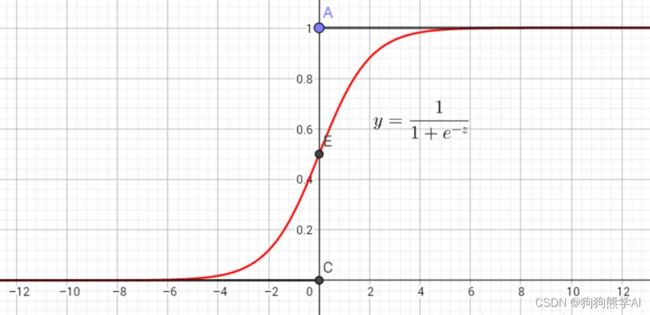
  用线性回归模型的预测结果去逼近真是标记的对数几率，将该模型称为 “对数几率回归”（logistic regression）。

4.2 策略

  使用极大似然法来估计参数w和b。
步骤一：确定概率 质量/密度 函数
    便于讨论，令$\beta =(\mathbf{w};b),\hat{x}=(\mathbf{x};1),p_1(\hat{x};\beta )=p(y=1|\hat{\mathbf{x}};\beta )，p_0(\hat{x};\beta )=p(y=0|\hat{\mathbf{x}};\beta )=1-p_1(\hat{x};\beta )$
$$p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=y_i{p}_1(\widehat{{\mathbf{x}}_{\mathbf{i}}};\beta )+(1-y_i)p_0(\widehat{{\mathbf{x}}_{\mathbf{i}}};\beta )$$
步骤二：写出极大似然函数
    给定数据集${({\mathbf{x}}_{\mathbf{i}},y_i)}_{i=1}^m$，对率回归模型最大化“对数似然”（likelihood）为：
$$\ell (w,b)=\sum _{i=1}^{m}lnp(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)$$
代入概率 质量/密度 函数，则最大化上式等价于最小化下式：
$$\ell (\beta )=\sum _{i=1}^m\left(-y_i{\beta }^{\mathbf{T}}\widehat{{\mathbf{x}}_{\mathbf{i}}}+ln(1+e^{{\beta }^{\mathbf{T}}\widehat{{\mathbf{x}}_{\mathbf{i}}}})\right)$$

4.3 求解算法

  4.2中的最终目标函数$\ell (\beta )$是关于β的高阶可导连续凸函数，可采用梯度下降法（gradient descent method）或牛顿法（Newton method）等求得最优解。
  如采用牛顿法，对于式子${\beta }^{\ast }=\underset{\beta }{\arg }min\ell (\beta )$，其第t+1轮迭代解的更新公式为：
$${\beta }^{t+1}={\beta }^t-{\left(\frac{{\partial }^2\ell (\beta )}{\partial \beta \partial {\beta }^T}\right)}^{-1}\frac{\partial \ell (\beta )}{\partial \beta }$$
  其中：$\frac{\partial \ell (\beta )}{\partial \beta }=-{\sum }_{i=1}^m\widehat{{\mathbf{x}}_{\mathbf{i}}}(y_i-p1(\widehat{{\mathbf{x}}_{\mathbf{i}}};\beta )),\frac{{\partial }^2\ell (\beta )}{\partial \beta \partial {\beta }^T}={\sum }_{i=1}^m\widehat{{\mathbf{x}}_{\mathbf{i}}}{\widehat{{\mathbf{x}}_{\mathbf{i}}}}^{\mathbf{T}}{p}_1(\widehat{{\mathbf{x}}_{\mathbf{i}}};\beta )(1-p_1(\widehat{{\mathbf{x}}_{\mathbf{i}}};\beta ))$

5、线性判别分析

5.1 模型

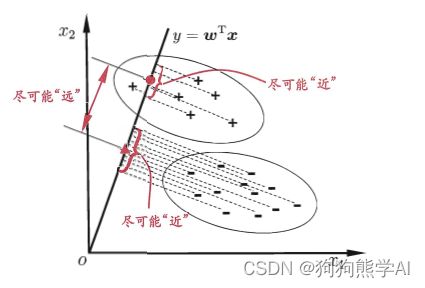
  线性判别分析（Linear Discriminant Analysis，简称LDA）方法尝试找到一个这样的分类边界：同类样例在该边界上的投影点尽可能靠近、异类样例的投影点尽可能远离，且各类中心间的距离尽可能大。

5.2 策略

  尝试将LDA的模型思想用数学方式表达。

同类样例在该边界上的投影点尽可能靠近$\leftrightarrow$同类样例投影点的方差尽可能小
各类中心间的距离尽可能大$\leftrightarrow$可用向量模长来度量

  从而得到欲最大化的目标函数$J=\frac{\Vert {{\mathbf{w}}^{\mathbf{T}}{\mu }_0-{\mathbf{w}}^{\mathbf{T}}\mu }_1{\Vert }_2}{{\mathbf{w}}^{\mathbf{T}}{\sum }_0\mathbf{w}+{\mathbf{w}}^{\mathbf{T}}{\sum }_1\mathbf{w}}=\frac{{\mathbf{w}}^{\mathbf{T}}({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^{\mathbf{T}}\mathbf{w}}{w^T({\sum }_0+{\sum }_1)w}$
  定义：
    “类内散度矩阵”：$S_w=\sum _{x\in X_0}(x-{\mu }_0)(x-{\mu }_0{)}^T+\sum _{x\in X_1}(x-{\mu }_1)(x-{\mu }_1{)}^T={\sum }_0+{\sum }_1$
    “类间散度矩阵”：$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$

  从而$J=\frac{{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{w}}{{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{w}}$，该式也称$S_b,S_w$的“广义瑞利商”。
  又因为其分子、分母都是关于w的二次项，所以其大小与w的长度无关，而只与其方向有关。而样例集确定后，μ₀、μ₁也为常值，不失一般性可令${\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{w}=1$，所以最终的优化目标如下：
$$\begin{array}{rl}& \\ & \underset{w}{\min }-{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{w}\\ & s.t.{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{w}\end{array}$$

5.3 求解算法

  可使用拉格朗日乘子法求解。
  由拉格朗日乘子法，上式等价于${\mathbf{S}}_{\mathbf{b}}\mathbf{w}=\lambda {\mathbf{S}}_{\mathbf{w}}\mathbf{w}$，其中$\lambda$为拉格朗日乘子。因为${\mathbf{S}}_{\mathbf{b}}\mathbf{w}$的方向恒为${\mu }_0-{\mu }_1$，不妨令${\mathbf{S}}_{\mathbf{b}}\mathbf{w}=\lambda ({\mu }_0-{\mu }_1)$，代入目标函数即可的：$$\mathbf{w}={\mathbf{S}}_{\mathbf{w}}^{-1}({\mu }_0-{\mu }_1)$$

5.4 其他补充

1. 以上考虑的是二分类的情况，可证明，当两类数据同先验、满足高斯分布且协方差相等时，LDA可达到最优分类。
2. LDA可推广到多分类任务中，其中推广定义：

  全局散度矩阵：${\mathbf{S}}_{\mathbf{t}}={\mathbf{S}}_{\mathbf{b}}+{\mathbf{S}}_{\mathbf{w}}={\sum }_{\mathbf{i}=1}^{\mathbf{m}}({\mathbf{x}}_{\mathbf{i}}-\mu )({\mathbf{x}}_{\mathbf{i}}-\mu {)}^{\mathbf{T}}$,其中$\mu$为所有示例的均值向量。

  类内散度矩阵：${\mathbf{S}}_{\mathbf{w}}=\sum {\mathbf{i}=1}^{\mathbf{N}}{\mathbf{S}}_{{\mathbf{w}}_{\mathbf{i}}}={\sum }_{\mathbf{i}=1}^{\mathbf{N}}\sum _{\mathbf{x}\in {\mathbf{X}}_{\mathbf{i}}}(\mathbf{x}-{\mu }_{\mathbf{i}})(\mathbf{x}-{\mu }_{\mathbf{i}}{)}^{\mathbf{T}}$\

  从而${\mathbf{S}}_{\mathbf{b}}={\mathbf{S}}_{\mathbf{t}}-{\mathbf{S}}_{\mathbf{w}}={\sum }_{\mathbf{i}=1}^{\mathbf{N}}{\mathbf{m}}_{\mathbf{i}}({\mu }_{\mathbf{i}}-\mu )({\mu }_{\mathbf{i}}-\mu {)}^{\mathbf{T}}$

3. LDA可通过投影来减小样本点的维数，且投影过程使用了类别信息，因此LDA也是经典的监督降维技术。

6、多分类学习

  N个类别C₁，C₁，…，C_N，多分类的基本思路是“拆解法”，即将多分类任务拆解为若干个二分类任务求解。通过任务拆分各自求解，再对结果进行继承以获得最终的多分类结果。
  常见的拆分策略由以下三种：

6.1 “一对一”

  “一对一”（One vs. One，简称OvO）将N个类别两两配对，从而产生$\frac{\mathbf{N}(\mathbf{N}-1)}{2}$个二分类任务，训练得到对应数目个二分类器。在测试阶段，新样本在所有分类器上都将产生一个结果，最终分类结果可以通过投票产生：即把预测最多的类别最为最终的分类结果。

6.2 “一对其余”

  “一对其余”（One vs. Rest，简称OvR）每次将一个类的样例作为正例、所有其他类的样例作为反例来训练N个二分类器。测试阶段，若仅有一个分类器将新样本视为正类，则对应的类别标记即为其最终分类结果；若有多个分类器将新样本视为正类，则可考虑个分类器的置信度，选择置信度最大的类别标记作为分类结果。

6.3 “多对多”

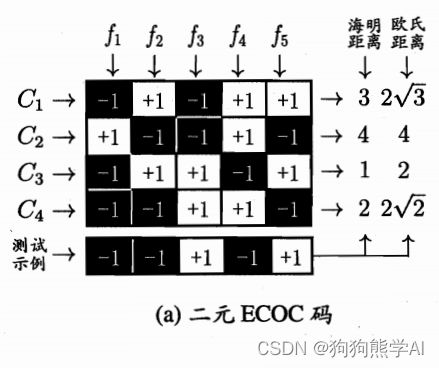
  “多对多”（many vs. msny）每次将若干类作为正类、若干个其他类作为反类。其正反类构造必须有特殊设计，如常用的“纠错输出码”（Error Correcting Output Codes，简称ECOC），其主要有两个步骤：

1. 编码 ：N个类别进行M次划分，每次划分一部分作为正例、一部分作为反例，形成M个二分类训练集，进而产生M个二分类器。
2. 解码 ：M个而分类器对新样例进行预测，所有预测结果组成一个编码，将该编码与每个类别各自的编码比较，选择编码距离最小的类别标记作为分类结果。
   

如图所示，共有4个类别，进行了5次划分，因此得到了5个分类器

7、类别不平衡问题

  类别不平衡（class-imbalance）指分类任务中不同类别的训练样例数目差别很大。可通过使用“欠采样”（undersampling）、“过采样”（oversampling）或着“阈值移动”（threshold-moving）等方法进行一定程度的改善。

8、补充

• Datawhale讲解视频