斐波那契数列、素数、质数和猴子吃桃问题

1. 什么是斐波那契数列、素数、质数和猴子吃桃问题？

1.1. 什么是斐波那契额数列

斐波那契数列（Fibonacci Sequence）是由如下形式的一系列数字组成的：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

上述数字序列中反映出来的规律，就是下一个数字是该数字前面两个紧邻数字的和，具体如下所示：

• 最开始的两个数字是0和1，第三个数字是前两个数字的和，即0+1=1，所以第三个数字是1
• 第四个数字是它前面紧邻的两个数字的和，即1+1=2，所以第四个数字是2
• 第五个数字是它前面紧邻的两个数字的和，即1+2=3，所以第五个数字是3
• 第六个数字是它前面紧邻的两个数字的和，即2+3=5，所以第六个数字是5
• 依此类推，即可推导出斐波那契数列中的更多组成数字。

示例：比如上述斐波那契数列中的最后两个数，可以推导出34后面的数为21+34=55

下面是一个更长一些的斐波那契数列：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …

在上述的斐波那契数列中，317811后面的数应该是196418+317811=514229，即514229。

1.1.1. 构造螺旋曲线

当我们是用斐波那契数列中的数字作为边长构建正方形的时候，可以构造出如下图所示的漂亮螺旋曲线：
你能看出上述正方形是如何对得在一起构造出螺旋曲线的规律吗？
比如5+8=13，即将边长为5和边长为8的两个正方形堆叠在一起，形成边长为13的一条边，再以13为边长构建正方形。此时边长为8的正方形与边长为13的正方形又会形成一个新的边厂为21的边，再以这个边长为21的边构造正方形。依此类推即可。

螺旋曲线在自然界中的契合。
See: Nature, The Golden Ratio, and Fibonacci

1.1.2. 规则

斐波那契数列可以被写为某种规则（关于数列构造规则，参见Sequences and Series）获得更详细的信息。

首先，数列中的项是从0开始向上增加的，具体如下表所示：

n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	…
xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	…

在上表中，索引用n表示，索引n对应的索引值用xn表示，所以上述的索引为6的索引为x6为8。
数列中的索引8对应的数是索引7和索引6对应的两个索引值的和，即x8=x7+x6
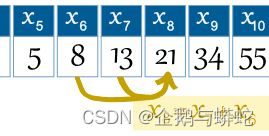由此，就可以将这个规则写为如下形式：
由此，就可以将这个规则写为如下形式：

xn = x[n−1] + x[n−2]

其中：

• xn 是索引n所对应的索引值
• xn−1 是索引n前面的索引n-1对应的索引值
• xn−2 是索引n-1前面的索引n-2对应的索引值

依据上述规则，索引9的值可以通过如下公式计算出来：

x9= x9−1 + x9−2

​ = x8 + x7

​ = 21 + 13

​ = 34

1.1.3. 斐波那契数列中负数方向的构成

斐波那契数列再负数方向也是成立的。下表是负数方向的构成：

n =	…	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	…
xn =	…	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	…

下面看下上表中反映出来的规律：

• 负数方向第一个数字，即索引为-1的时候，对应的索引值为1-0=1，所以-1索引处对应的索引值为1
• 负数方向第二个数字，即索引为-2的时候，对应的索引值为0-1=-1，所以-2索引处对应的索引值是-1
• 负数方向第三个数字，即索引为-3的时候，对应的索引值为1-(-1)=2，所以-3索引处对应的索引值是2
• 负数方向第四个数字，即索引为-4的时候，对应的索引值为-1-2=-3，所以-4索引处对应的索引值是-3
• 依此类推，-n-2处对应的索引值是-n处索引值x[-n]减去-n-1处的索引值x[-n-1]，所以大致规律为x[-n-2]=x[-n]-x[-n-1]，此处n>=0。

1.1.4. 历史

Fibonacci并不是第一个知道这个数列的人，这个数列实际上早在斐波那契发现之前的几百年前就已经被印度人发现了。
### 1.1.5. 关于斐波那契（Fibonacci）这个人

斐波那契的真实名字是Leonardo Pisano Bogollo，他生活在公元1170-1250年的意大利。

"Fibonacci"是他的绰号，大致是Bonacci的儿子这个意思。

与斐波那契数列一样出名的是，他帮助推广了阿拉伯数字（Hindu-Arabic Numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)）在欧洲的使用，并且最终替代了罗马数字（Roman Numerals (I, II, III, IV, V, etc)）。这在数学表达上解决了很多麻烦，很感谢Leonardo。

1.1.6. 斐波那契日（Fibonacci Day）

每年的11月23日是斐波那契日，之所以取这个日期，是取自斐波那契数列中的4个连续数字 “1, 1, 2, 3”。

1.2. 什么是质数（素数）

1.2.1. 质数

质数，又称为素数，是指大于1，且只能被1和自身整除的整数。

比如：2，3，5，7，11，13等等，这些都是只能被1和自身整除的整数，所以它们都是质数。

1.2.2. 质数中不包含1

几年前，质数中是包含1的，但现在质数中并不包含1，所以现在1并不是质数。即1既不是质数，也不是合数。

关于质数和合数：

• 当一个数字可以被1和自身之外的其他数字整除的时候，那么这个数就是合数
• 当一个数字不能被1和自身之外的其他数字整除的时候，那么这个数就是质数

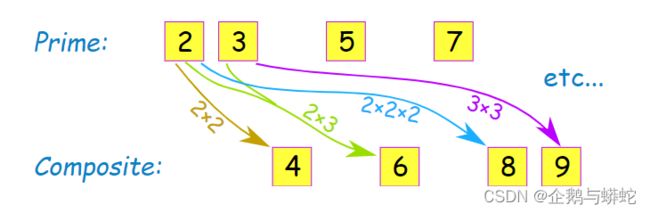
因为6能被2和3整除，所以6合数；而7只能被1和自身7整除，所以7是质数。

具体如下图所示：

### 1.2.3. 不包含小数

这里我们讨论的范围是整数，而并不包含小数、分数。

1.2.4. 因数

可以使用因数定义质数。

所谓的因数，是指相乘在一起得到另外一个数，那么这两个相乘的数就称为乘积所得到数的因数。比如上图中，2和3是6这个数的因数，因为2x3=6。

当一个数的因数只有1和这个数本身的时候，那么这个数就是质数。

与我们之前对质数的定义一致，只是使用因数描述质数而已。

另外，需要注意的是，在谈论质数的时候，条件是大于1的正整数，分数、小数、负数、0和1都不在讨论范畴之内。

比如下面的表中，3是质数，6是合数。

3 = 1 × 3 (the only factors are 1 and 3)	Prime
6 = 1 × 6 6 = 2 × 3 (the factors are 1, 2, 3 and 6)	Composite

1到14这14个数中，质数和合数分别如下表所示：

Number	Can be Exactly Divided By	Prime, or Composite?
1	(1 is not prime or composite)
2	1, 2	Prime
3	1, 3	Prime
4	1, 2, 4	Composite
5	1, 5	Prime
6	1, 2, 3, 6	Composite
7	1, 7	Prime
8	1, 2, 4, 8	Composite
9	1, 3, 9	Composite
10	1, 2, 5, 10	Composite
11	1, 11	Prime
12	1, 2, 3, 4, 6, 12	Composite
13	1, 13	Prime
14	1, 2, 7, 14	Composite
…	…	…

注意：

1既不是质数，也不是合数。

1.3. 什么是猴子吃桃问题

问题描述：

猴子第一天摘下若干个桃子，立即吃了一半，还不过瘾又多吃了一个，第二天将第一天剩下的桃子吃了一半又多吃了一个，以后每天以这个规律吃下去，到第十天再去吃时发现只剩下一个桃子，问猴子第一天摘了多少个桃子？

问题分析：

已知第十天剩下的桃子个数a10为1，即第十天有a10个桃子；假设第九天的桃子数量为a9，那么a9-(a9/2+1)=a10，求解出a9=2*(a10+1)，即第十天剩下的桃子数量加1的和，乘以2，就是第9天剩下的桃子数量。

同理，假设第八天的桃子数量为a8，那么a8-(a8/2+1)=a9，a8=2*(a9+1)，即第八天剩下的桃子数量是第九天的桃子数量加1的和，乘以2，得到的结果就是第八天的桃子数量。

依此类推，可以求出第一天剩下的桃子数量为a1=2*(a2+1)。

上述分析过程，就找出了桃子数量与天数之间的关系。这个过程使用递归函数，就很容易求解了。通过递归函数，求出第一天剩下的桃子数量，然后就可以求出总的桃子数量了。

解决问题：

有了天数与桃子数量之间的对应关系，接下来就可以编码解决问题了。具体如下所示：

def monkey_peach(n):
 if n == 10:
     return 1
 else:
     return (monkey_peach(n + 1) + 1) * 2


print('There are %d peaches on 1st day' % monkey_peach(1))            # print: 1534

peaches1st = monkey_peach(1)
print('桃子的总数为：%d' % ((peaches1st+1)*2))

知道了第1天剩下的桃子数量，那就知道总数是多少了。因为第一天吃掉了一半+1个桃子，假设总数为n个桃子，那么第一天剩下的条子数量为：n-(n/2+1)=1534。所以，此处n=(1534+1)*2 = 3070。所以桃子的总数是3070个。

上述代码的执行结果如下所示：

There are 1534 peaches on 1st day
桃子的总数为：3070

至此，就求解了问题。

验证答案：

使用正向分析的方式，按照数学方程式的方式，构建方程，查找方程与天数之间的关系，并最终求的结果。

假设桃子总数为n，
那么第一天吃掉的桃子数量为n/2+1，
第一天剩下的桃子数量为：n-(n/2+1) -> n/2-1，即2^(-1)*n-1
第二天吃掉的桃子数量为：(n/2-1)/2+1，
第二天剩下的桃子数量为：(n/2-1)-((n/2-1)/2+1) -> n/4-3/2，即2^(-2)*n-2^(-2)*(2²-1)
第三天吃掉的桃子数量为：(n/4-3/2)/2+1，
第三天剩下的桃子数量为：(n/4-3/2)-((n/4-3/2)/2+1) -> n/8-7/4，即2^(-3)*n-2^(-3)*(2³-1)

从上述第二天和第三天剩下的桃子数量的表达式中可以找出剩下的桃子数量与天数之间存在指数关系。即2的负天数次幂的结果乘以桃子总数n的乘积，减去2的负天数次幂与2的正天数次幂减1的差的乘积的结果，就是某天剩下的桃子数量。

按照上述关系表达式，第10天剩下的桃子数量为：2^(-10)*n-2^(-10)*(2¹⁰-1)，而这个表达式的值为1。

即2^(-10)*n-2^(-10)*(2¹⁰-1)=1 -> n=2¹⁰+2¹¹-2，从这个表达式就可以求出n的值为3070。由此证明上述的递归调用
函数求得的结果是正确的。

2. 列表支持的所有方法

2.1. list类型对象简介

列表（list类型对象）是可变类型，用于顺序存储其它类型的对象。Python中的list类型对象中可以包含多种数据类型对象。具体如下所示：

In [47]: l = []
In [48]: l.append(1)
In [49]: l
Out[49]: [1]
In [50]: l.append('a')
In [51]: l
Out[51]: [1, 'a']
In [52]: l.append((5,))
In [53]: l
Out[53]: [1, 'a', (5,)]
In [54]:

上述的iPython中的结果显示，list类型对象l中可以存储整数、字符、tuple类型对象等。

有多种方式可以用于构建list类型对象，具体如下所示：

• 使用一对空的中括号构建一个空的list类型对象：l = []就是这种构建形式。
• 使用中括号构建list类型对象，同时中括号中包含列表项，如果多于1个列表项，各个列表项之间需要用英文半角逗号分隔：m = [1], n = [1, 2, 'a']，这种形式构建具有初始内容的列表对象。
• 使用列表推导式构建具有初始内容的列表对象：[x for x in iterable]，比如[x for x in range(1,10)]。
• 使用list类型对象的构造函数构建list类型的对象：list(iterable)，比如list(range(1,10))。

2.2. list类型对象支持的方法函数

1. list.append：向列表对象末尾追加对象。具体如下所示：

   • 向列表中追加单个对象：

     a = []
     a.append(5)
     

     上述就向列表中增加了一个单一对象。

   • 像列表中追加可迭代对象：

     b = tuple(range(0,3))
     a.append(b)
     

     此时列表对象a中的结果为：[5, (0, 1, 2)]，append方法并不会把可迭代类型展开之后追加到列表对象的末尾。

2. list.clear：移除列表对象中的所有项目。

   具体如下所示：

   In [64]: a
   Out[64]: [5, (0, 1, 2)]
   In [65]: a.clear()
   In [66]: a
   Out[66]: []
   

   上述clear()方法调用完成之后，就将列表对象a中的项目清空了。

3. list.copy：返回列表的浅拷贝。

   浅拷贝并不会递归创建被拷贝的对象，只是对被拷贝对象的引用。所以在通过浅拷贝创建了新的对象之后，如果对初始被拷贝对象进行修改，那么修改会直接反应在拷贝新生成的对象上面。
   
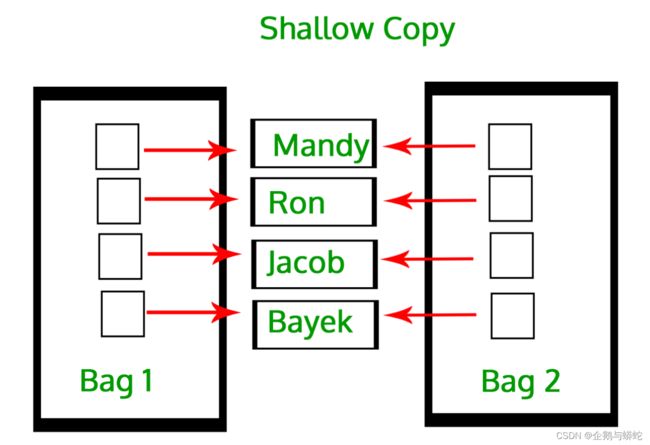
   从上图中可以看出，浅拷贝生成的额Bag2只是引用了被拷贝对象Bag1的对象，并没有创建新的对象。

   用代码演示浅拷贝，如下所示：

   In [120]: li1 = [1, 2, [3,5], 4]
   In [121]: li2 = li1.copy()
   In [122]: li2[2][0] = 7
   In [123]: li2
   Out[123]: [1, 2, [7, 5], 4]
   In [124]: li1
   Out[124]: [1, 2, [7, 5], 4]
   In [125]:
   

   上述带啊吗反映出来的结果可以看出，拷贝后对嵌套在li2列表对象中的子列表中元素的修改会直接反应到初始被拷贝列表对象li1上面。说明浅拷贝只是将对象引用关系拷贝到新的变量名中。并不会递归创建与被拷贝对象相同的对象。

4. list.count：统计列表中各个项目出现的次数。

   这个方法函数的效果如下所示：

   In [133]: m = [1, 2, 3, 2, 4, 2]
   In [134]: m.count(2)
   Out[134]: 3
   

   上述代码中，统计了项目2在列表对象m中出现的次数。输出结果3表示项目2在列表m中总共出现了3次。

5. list.extend：向列表对象末尾追加项目。如果被追加项目是单个元素，效果与list.append方法函数相同；如果被追加的项目是可迭代元素，那么这个方法会将可迭代对象展开之后按照原顺序追加到列表对象中。

   这个方法函数的效果如下所示：

   In [136]: b
   Out[136]: (0, 1, 2)
   In [137]: m
   Out[137]: [1, 2, 3, 2, 4, 2]
   In [138]: m.extend(b)
   In [139]: m
   Out[139]: [1, 2, 3, 2, 4, 2, 0, 1, 2]
   

   上述并不会将tuple对象b直接以tuple对象的形式追加到列表对象m中，而是将其展开之后逐个按顺序加入到列表对象m中。

6. list.index：返回列表中指定元素第一次出现的索引位置。如果指定的元素在列表中不存在，则抛出ValueError异常。

   这个方法函数的效果如下所示：

   In [142]: m
   Out[142]: [1, 2, 3, 2, 4, 2, 0, 1, 2]
   In [143]: m.index(2)
   Out[143]: 1
   

   上面的列表对象m中有多个2出现，那么m.index(2)返回第一次出现的索引位置，所以结果为1。

7. list.insert：像列表对象指定的索引位置前面插入一个项目。

   该方法函数的效果如下所示：

   In [145]: li1
   Out[145]: [1, 2, [7, 5], 4]
   In [146]: li1.insert(2, 9)
   In [147]: li1
   Out[147]: [1, 2, 9, [7, 5], 4]
   

   上述li1.insert(2, 9)方法表示在列表对象li1的索引位置2的前面插入一个项目9。

8. list.pop：从列表对象中移除指定索引位置的项目，索引值为-1表示李彪对象中最后一个项目。如果指定的索引不存在，那么会抛出IndexError异常。

   该方法函数的效果如下所示：

   In [149]: li1
   Out[149]: [1, 2, 9, [7, 5], 4]
   In [150]: li1.pop(-1)
   Out[150]: 4
   In [151]: li1
   Out[151]: [1, 2, 9, [7, 5]]
   

   上述代码中，li1.pop(-1)表示从列表对象中移除最后一个项目，即4。该函数调用完成之后，会返回该索引位置的项目作为返回值。

9. list.remove：从列表对象中移除第一个出现的被指定的项目。如果被指定的项目在列表中不存在，那么会抛出ValueError异常。

   该方法函数的效果如下所示：

   In [153]: m
   Out[153]: [1, 2, 3, 2, 4, 2, 0, 1, 2]
   In [154]: m.remove(2)
   In [155]: m
   Out[155]: [1, 3, 2, 4, 2, 0, 1, 2]
   

   list.remove(2)方法移除了列表中第一次出现的2这个项目。

10. list.reverse：将列表对象中的各个项目前后位置就地翻转，即前变后，后变前。

    这个方法函数的效果如下所示：

    In [157]: li1
    Out[157]: [1, 2, 9, [7, 5]]
    In [158]: li1.reverse()
    In [159]: li1
    Out[159]: [[7, 5], 9, 2, 1]
    

    上述代码可以看出，列表中项目的前后顺序被翻转了。

11. list.sort：就地对列表对象中的项目排序，该操作会直接修改列表本身。

    该方法函数的效果如下图所示：

    In [163]: m
    Out[163]: [1, 3, 2, 4, 2, 0, 1, 2]
    In [164]: m.sort()
    In [165]: m
    Out[165]: [0, 1, 1, 2, 2, 2, 3, 4]
    In [166]: m.sort(reverse=True)
    In [167]: m
    Out[167]: [4, 3, 2, 2, 2, 1, 1, 0]
    

    上述输出中显示，默认情况下，是按照升序对列表对象中的项目进行排序的。如果在方法调用的时候，指定参数reverse=True，那么就可以实现降序排列的效果。

3. 实现一个简易的计算器

效果如下：

运行后提示让用户输入一个数字，然后提示输入操作符（+ - * /），再次提示输入一个数字，打印计算结果，在不退出程序的前提下，可以允许用户继续输入新一组数据计算。

代码实现：

代码的具体内容如下所示：

import sys

def calculator():
 while True:
     num1 = input('Please enter the first number: ')
     optr = input('Please enter the operator [+ - * /]: ')
     num2 = input('Please enter the second number: ')

     expr = str(num1) + optr + str(num2)
     print(num1, optr, num2, '=', eval(expr))

     again = input('Do you wana again? [y/n]: ')
     if str.lower(again) == 'n':
         sys.exit(0)
     else:
         pass

calculator()

上述代码的执行过程如下所示：

Please enter the first number: 5
Please enter the operator [+ - * /]: /
Please enter the second number: 2
5 / 2 = 2.5
Do you wana again? [y/n]: y
Please enter the first number: 3
Please enter the operator [+ - * /]: -
Please enter the second number: 2
3 - 2 = 1
Do you wana again? [y/n]: n

Process finished with exit code 0

上述代码是可以正常工作的。

4. References

[1]. Fibonacci Sequence

[2]. Prime Composite Number