2020_CIKM_Partial Relationship Aware Influence Diffusion via a Multi-channel Encoding Scheme for Soc

[论文阅读笔记]2020_CIKM_Partial Relationship Aware Influence Diffusion via a Multi-channel Encoding Scheme for Social Recommendation

论文下载地址： https://doi.org/10.1145/3340531.3412016
发表期刊：CIKM
Publish time: 2020
作者及单位:

• Bo Jin Dalian University of Technology Dalian, China [email protected]
• Ke Cheng Dalian University of Technology Dalian, China [email protected]
• Liang Zhang∗ Dongbei University of Finance and Economics Dalian, China [email protected]
• Yanjie Fu University of Central Florida Orange City, FL [email protected]
• Minghao Yin Northeast Normal University Changchun, China [email protected]
• Lu Jiang Northeast Normal University Changchun, China [email protected]

数据集： 正文中的介绍

• Yelp (用的Diffet)
• Flickr (用的Diffet)

代码：

• （作者没给）

其他：

其他人写的文章

简要概括创新点： 用的DiffNet的数据集，可能就是针对DiffNet++进行挑战的。①channel就是embedding的dimension。 ②multi-label就是 user-多个item(label)。③partial relationship就是因为某些关系形成的子连通域（子图）。④Atttention是以a channel-wise way进行的，传统的是以node-wise way进行的，其实是更精细化了。⑤数据集本身就是稀疏的，SoRec本来就是为了解决稀疏性，本文就说恰好基于稀疏性，有点面向数据编程了(如果不稀疏的话，计算量就bao了)

• (3) In light of this, we propose MEGCN (Multi-channel Encoding Graph Convolutional Network), a partial relationship aware influence diffusion model, for social recommendation. (有鉴于此，我们提出了一种 基于部分关系的影响扩散模型 MEGCN（Multi-channel Encoding Graph Convolutional Network），用于社会推荐。)
  • The key idea behind this model is a feature-wise message computation with sparse regularization in the influence diffusion process . (该模型背后的关键思想是在 影响扩散过程 中采用 稀疏正则化 的 特征信息计算。)
  • More specifically, the layer-wise diffusion process starts with an initial embedding for each user, which can be a free vector that captures the latent interest or any explicit features. (更具体地说，分层扩散过程 从每个用户的初始嵌入开始，该嵌入可以是捕获潜在兴趣或任何显式特征的自由向量。)
  • Then a GCN-like information aggregation is conducted in each layer, which can help capture neighborhood contexts. At its core, under the assumption of channel-wise graph sparsity, the traditional node-wise message computation is changed into feature-wise computation, such that user interests and shared interests will be simultaneously captured in the layer-wise inforation diffusion process. (然后在每一层中进行 类似GCN 的信息聚合，这有助于捕获邻域上下文。其核心是在 信道图稀疏的假设下 ，将传统的节点消息计算 转化为 特征计算 ，从而在 分层信息扩散过程 中同时捕获用户兴趣和 共享兴趣。)
• In the data preparation step, we filter out users with less than 2 historical action records and 2 social neighbors in both datasets. (在数据准备阶段，我们筛选出两个数据集中历史动作记录和社交邻居少于2个的用户。)

ABSTRACT

• (1) Social recommendation tasks exploit social connections to enhance recommendation performance. (社会推荐任务利用社会关系来提高推荐性能。)
• (2) To fully utilize each user’s first-order and high-order neighborhood preferences, recent approaches incorporate influence diffusion process for better user preference modeling. (为了充分利用每个用户的一阶和高阶邻域偏好，最近的方法结合了影响扩散过程，以便更好地进行用户偏好建模。)
• (3) Despite the superior performance of these models, they either neglect the latent individual interests hidden in the user-item interactions or rely on computationally expensive graph attention models to uncover the item-induced sub-relations, which essentially determine the influence propagation passages. (尽管这些模型的性能优越，但它们要么忽略了隐藏在用户-项目交互中的潜在个人兴趣，要么依赖计算昂贵的图形注意模型来揭示项目诱导的子关系，这些子关系本质上决定了影响的传播通道。)
• (4) Considering the sparse substructures are derived from original social network, we name them as partial relationships between users. (考虑到稀疏子结构源自原始社交网络，我们将其命名为用户之间的部分关系。)
• (5) We argue such relationships can be directly modeled such that both personal interests and shared interests can propagate along a few channels (or dimensions) of latent users’ embeddings. (我们认为这种关系可以直接建模，这样个人兴趣和共享兴趣都可以通过潜在用户嵌入的几个渠道（或维度）传播。)
• (6) To this end, we propose a partial relationship aware influence diffusion structure via a computationally efficient multi-channel encoding scheme. (为此，我们通过一种计算高效的多通道编码方案，提出了一种部分关系感知的影响扩散结构。)
  • Specifically, the encoding scheme first simplifies graph attention operation based on a channel-wise sparsity assumption, (具体而言，编码方案首先基于信道稀疏性假设 简化了图注意操作，)
  • and then adds an InfluenceNorm function to maintain such sparsity. (然后添加一个InfluenceNorm函数来保持这种稀疏性。)
  • Moreover, ChannelNorm is designed to alleviate the oversmoothing problem in graph neural network models. (此外，ChannelNorm被设计用于缓解图神经网络模型中的过度平滑问题。)
• (7) Extensive experiments on two benchmark datasets show that our method is comparable to state-of-the-art graph attention-based social recommendation models while capturing user interests according to partial relationships more efficiently. （在两个基准数据集上的大量实验表明，我们的方法可以与最先进的基于图形注意的社会推荐模型相媲美，同时可以更有效地根据部分关系捕获用户兴趣。）

CCS CONCEPTS

• Human-centered computing → Social recommendation; • Information systems → Recommender systems.

KEYWORDS

Social Network; Recommendation; Graph Neural Network

1 INTRODUCTION

• (1) Discerning user preference with sparse user behavior data is a key issue in a recommendation task. The social recommendation has emerged as a pioneering direction based on the social influence theory which states connected people would show similar interests pattern [30, 33, 35, 39]. (在推荐任务中，利用稀疏的用户行为数据识别用户偏好是一个关键问题。社会推荐是基于社会影响理论的一个开创性方向，该理论指出，有关联的人会表现出相似的偏好模式[30、33、35、39]。)

  • Ideally, a successful social recommendation system should capture temporal or evolutionary individual interests and shared interests. Hence uncovering self interests [2] hidden in user-item interactions while identifying the shared interests according to social influence become the most essential. （理想情况下，一个成功的社会推荐系统应该能够捕捉到 暂时的 或 进化的 个人兴趣和共同的兴趣。因此，发现隐藏在用户项目交互中的 自我兴趣 [2]，同时根据社会影响确定 共享兴趣 成为最重要的。）
  • However, unlike single-label graph learning tasks, a recommendation system based on social network is usually a multi-label graph learning task with extreme label (or user-item interaction) sparsity. (然而，与 单标签图学习任务 不同，基于社交网络的推荐系统通常是具有 极端标签（或用户项交互）稀疏性 的 多标签图学习任务 。)
  • In fact, it is the sparse label-induced social relationship substructures [4, 37] that determine the social influence channels. (事实上，决定社会影响渠道 的是 稀疏标签诱导的社会关系子结构 [4,37]。)
  • As a result, the traditional assumption that linked users in a social network tend to share the same interests no longer fits for all the users. (因此，社交网络中链接用户倾向于共享相同兴趣的传统假设不再适用于所有用户。)
    • For instance, Figure 1 illustrates the frequency distribution of similar behaviors between each user and all neighbors according to social network structure of Yelp and Flickr. The right-skewed distributions demonstrate though users in social network show some similar behaviors with neighborhoods, they largely maintain their own interests. Therefore, it is of utmost importance to capture social influence according to sparse substructures rather than the original social network structures. (例如，图1显示了根据Yelp和Flickr的社交网络结构，每个用户和所有邻居之间相似行为的频率分布。右偏分布表明，尽管社交网络中的用户在社区中表现出一些类似的行为，但他们基本上维护了自己的兴趣。因此，根据稀疏的子结构而不是原始的社会网络结构来获取社会影响力至关重要。)
      

• (2) Previous studies for social recommendation attempt to model social effects in various ways, such as by trust propagation, regularization loss, matrix factorization, network embedding and deep neural networks [30, 31, 38]. However, these studies have some limitations. (之前的社会推荐研究试图以各种方式模拟社会效应，例如通过信任传播、正则化损失、矩阵分解、网络嵌入和深度神经网络[30,31,38]。然而，这些研究有一些局限性。)

  • First, most works model friends’ influence statically or dynamically without differentiating influence importance, (首先，大多数作品对朋友的影响力进行静态或动态建模，而不区分影响力的重要性)
    • such as spatial Graph Neural Network (GNN) approaches [11,30,36], which apparently ignore the differences of social effects, and will further lead to oversmoothing problems. (例如，空间图神经网络（GNN）方法[11,30,36]，它显然忽略了社会效应的差异，并将进一步导致过度平滑问题。)
  • Second, even though attention-based models [29–31] have been proposed to distinguish social effects, they mainly calculate the node-wise similarities, which are computationally expensive in large-scale social recommendation tasks. (第二，尽管基于注意的模型[29–31]被提出用于区分社会效应，但它们主要计算节点相似性，这在大规模社会推荐任务中计算成本很高。)
  • In essence, Diffnet++ [29] and DANSER [31] achieve superior performance because they model the label-substructures [4] by incorporating user-item interactions in the information diffusion process of the social network. (本质上，Diffnet++[29]和DANSER[31]实现了卓越的性能，因为它们通过在社交网络的 信息扩散过程中 结合用户项交互来建模 标签子结构 [4]。)
  • In our work, we name the label-induced substructures as partial relationships. Moreover, the light-weight convolution [28] inspires us that node-wise computational complexity can be mitigated by splitting the node representation into chunks. (在我们的工作中，我们将标签诱导的子结构命名为部分关系。此外，轻量级卷积[28]启发我们，可以通过将节点表示拆分为块来降低节点计算复杂性。)
    • Hence, we argue that such partial relationships can be directly reflected in each dimension of user embedding without using burdensome node-wise attention-based models. (因此，我们认为，这种局部关系可以直接反映在用户嵌入的每个维度上，而无需使用繁重的基于节点的注意模型。)

• (3) In light of this, we propose MEGCN (Multi-channel Encoding Graph Convolutional Network), a partial relationship aware influence diffusion model, for social recommendation. (有鉴于此，我们提出了一种 基于部分关系的影响扩散模型 MEGCN（Multi-channel Encoding Graph Convolutional Network），用于社会推荐。)

  • The key idea behind this model is a feature-wise message computation with sparse regularization in the influence diffusion process . (该模型背后的关键思想是在 影响扩散过程 中采用 稀疏正则化 的 特征信息计算。)
  • More specifically, the layer-wise diffusion process starts with an initial embedding for each user, which can be a free vector that captures the latent interest or any explicit features. (更具体地说，分层扩散过程 从每个用户的初始嵌入开始，该嵌入可以是捕获潜在兴趣或任何显式特征的自由向量。)
  • Then a GCN-like information aggregation is conducted in each layer, which can help capture neighborhood contexts. At its core, under the assumption of channel-wise graph sparsity, the traditional node-wise message computation is changed into feature-wise computation, such that user interests and shared interests will be simultaneously captured in the layer-wise inforation diffusion process. (然后在每一层中进行 类似GCN 的信息聚合，这有助于捕获邻域上下文。其核心是在 信道图稀疏的假设下 ，将传统的节点消息计算 转化为 特征计算 ，从而在 分层信息扩散过程 中同时捕获用户兴趣和 共享兴趣。)

• (4) We summarize the contributions of this paper as follows: (我们将本文的贡献总结如下：)

  • We propose MEGCN, a partial relationship aware influence diffusion model with channel-wise sparsity, to efficiently capture both self interests and share interests in the social recommendation tasks. (我们提出了一个具有 通道稀疏性 的 部分关系感知影响扩散模型 MEGCN，以有效地捕获社交推荐任务中的 自我兴趣 和 共享兴趣 。)
    • In the information diffusion process, MEGCN realizes feature-wise message computation under the graph channel-wise sparsity assumption. (在 信息扩散 过程中，MEGCN在 图通道稀疏性假设 下实现了 特征信息计算 。)
  • We design two normalization schemes, InfluenceNorm and ChannelNorm, to guarantee channel-wise sparsity, such that they can model partial relationships and alleviate the over-smoothing problem in graph convolution networks. (为了 保证信道稀疏性 ，我们设计了两种正则化方案 InfluenceNorm 和 ChannelNorm ，这样它们可以对部分关系进行建模，缓解图卷积网络中的 过度平滑 问题。)
  • We demonstrate the effectiveness of our model on two real world datasets. Experimental results show that MEGCN can achieve comparable recommendation performance to graph attention-based models with much less computational cost. (我们在两个真实数据集上展示了我们模型的有效性。实验结果表明，MEGCN能够以更低的计算成本实现与基于图形注意的模型相当的推荐性能。)

2 PRELIMINARIES

2.1 Problem Formalization

Definition 1 (partial relationship). (部分关系)

• (1) Unlike graph-based single-label learning tasks , a social recommendation task fundamentally involves a social network as well as a user-item interaction graph. Then, each user from the user-item interaction graph can be regarded as a node with multiple labels (i.e. items), which forms various label-substructures when combined with social network structures. (与 基于图的单标签学习任务 不同，社交推荐任务基本上涉及社交网络和用户项交互图。然后，用户项目交互图中的每个用户都可以被视为一个具有多个标签（即项目）的节点，当与社交网络结构结合时，这些标签会形成各种标签子结构。)
• (2) Consequently, self interests and shared interests can simultaneously propagate along the label-induced sub social networks structures, which are named as partial relationships between users. (因此，自我兴趣 和 共享兴趣可以沿着标签诱导的子社会网络结构 同时传播，这种子社会网络结构被称为用户之间的 部分关系。)

Definition 2 (graph with channel-wise sparsity). (具有通道稀疏性的图)

• (1) A graph has channel-wise sparsity when element-wise embedding multiplication between two neighbors results in a sparse embedding, of which non-zero dimensions form information passing channels. (当两个邻域之间的元素嵌入相乘得到稀疏嵌入时，图具有通道稀疏性，其中非零维形成信息传递通道。)
• (2) As a result, the sparse partial relationships can be modeled via using the sparse channels. (因此，可以通过使用稀疏通道对稀疏部分关系进行建模。)

============

• (1) In general, a social network can be described as a set of nodes and links, with nodes representation matrix $X$ and adjacency matrix $A$ containing link weights. The degree matrix $D_{ii}={\sum }_j{A}_{ij}$ represents the sum of all link weights to node $i$. In consistent with most studies, identity matrix $I$ is used in the graph Laplacian operation and help realize self-loop operation on the graph. (一般来说，社交网络可以描述为一组节点和链接，节点表示矩阵$X$和邻接矩阵$a$包含链接权重。度矩阵$D_{ii}={\sum }_j{a}_{ij}$表示节点$i$的所有链接权重之和。与大多数研究一致，单位矩阵$I$ 用于 图形拉普拉斯运算 并帮助在图形上实现 自循环运算。)

• (2) In a social recommendation system, there are two sets of entities (a user set $U$ and an item set $V$) and two graphs (a user-item interaction graph $R$ and a social network $S$). (在社交推荐系统中，有两组实体（用户集$U$和项目集$V$）和两个图形（用户项目交互图$R$和社交网络$S$）。)

  • Note that the interaction graph $R$ can be an explicit or implicit feedback-based rating graph. (请注意，交互图$R$可以是基于显式或隐式反馈的评分图。)
  • In particular, in an implicit user-item interaction scenario (e.g. purchasing an item, voting for a song), we let $r_{ai}$ denote the link weight between user $a$ and item $i$, and $r_{ai}$ is 1 if user $a$ interacted with item $i$, otherwise $r_{ai}$ is 0. (特别是，在一个隐式用户项交互场景中（例如，购买一个项目(物品)，为一首歌投票），我们让$r_{ai}$表示用户$a$和项$i$之间的链接权重，如果用户$a$与项$i$交互，则$r_{ai}$为1，否则$r_{ai}$为0。)
  • We let $d$ represent the number of channels or dimensions of an entity embedding, (我们让$d$表示实体嵌入的通道数或维度，)
  • $M$ denote the number of users in social network. ($M$表示社交网络中的用户数量。)
  • and $N$ denote the total number of links between users. ($N$表示用户之间的链接总数。)

• (3) Besides, the associated feature matrix $P$ and $Q$ of users (e.g, user profile) and items (item text representation, item visual representation)) are usually provided. (此外，通常会提供用户（例如用用户画像）和项目（项目文本表示、项目视觉表示）的相关特征矩阵$P$和$Q$。)

  • Then, the recommendation problem can be formalized as a link prediction task on the graph $R$: given $R$, $S$, $P$ and $Q$, a social recommendation aims to predict users’ unknown interests to items in $R$: $\tilde{R}=f(R,S,P,Q)$:. Given the problem definition, we introduce the preliminaries that are closely related to our proposed model. (然后，推荐问题可以形式化为 链接预测任务 在图$R$：给定$R$、$S$、$P$和$Q$，社交推荐旨在预测用户对$R$中项目的未知兴趣：$R:\tilde{R}=f（R，S，P，Q）$。给出了问题的定义，我们介绍了与我们提出的模型密切相关的预备工作。)

• (4) Note that social recommendation is a typical graph-based multilabel learning task with one user interacts with multiple items, which needs to model label-induced sub-relations among users. (请注意，社交推荐是一项 典型的基于图形的多标签学习任务 ，一个用户与多个项目交互，需要对 标签诱导的用户子关系进行建模。)

  • As explained before, our work aims to model such sparse relationships via channel-wise sparsity. (如前所述，我们的工作旨在通过通道稀疏性对此类稀疏关系进行建模)
  • After splitting the embedding of user $u$ into unit chunks [28], each chunk or channel of latent vector $X_u$ can be regarded as an independent information passage in user $u$’s ego network $S_u$, thus modeling the label-substructure relationships in the social network. (在将用户$u$嵌入到单元块中[28]之后，潜在向量$X_u$的每个块或通道可以被视为用户$u$的自我网络$S_u$中的独立信息通道，从而对社交网络中的 标签子结构关系 进行建模.)
  • Our work models such relationships in the aforementioned function $f$. In the rest of the paper, we use $\odot$ to represent element-wise multiplication. (我们的工作在上述函数$f$中对这种关系进行了建模。在本文的其余部分中，我们使用$\odot$表示 元素乘法 。)

2.2 Graph Convolutional Network

• (1) Graph Convolutional Network [3] models the graph message aggregation process as spectral convolution, in which node representations $g_{\theta }=diag(\theta )$ are transformed into Fourier domain with a filter parameterized by $\theta =R^d$: (图形卷积网络[3]将图形消息聚合过程 建模为 谱卷积，其中节点表示形式$g\theta =diag(\theta )$被转换到 傅立叶域 ，过滤器由$\theta =R^d$参数化：)
  
  • where $U$ is formed by eigenvectors of normalized graph Laplacian matrix $L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}=U\Lambda U^T$. ($U$由 归一化图拉普拉斯矩阵 的特征向量构成)
  • However, eigenvalue decomposition is computationally expensive. (然而，特征值分解的计算代价很高。)
  • Therefore, it was suggested that $g_{\theta }$ could be approximated by a truncated expansion in terms of Chebyshev polynomials $T_k(x)$ up to $K$-th order [12]: (因此，有人建议，$g_{t}heta$可以用截断展开式近似，即 切比雪夫多项式 $T_k（x）$到第$K$阶[12]：)
    
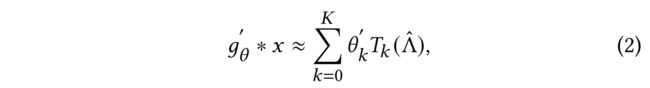
  • where$\hat{\Lambda }=\frac{2}{{\lambda }_{max}}\Lambda -I_N$ denotes the maximum eigenvalue of $L$, (表示$L的最大特征值$)
  • and ${\theta }_k^{\prime }$ is the vector of Chebyshev coefficients. (是切比雪夫系数的向量。)
• (2) In particular, when ${\lambda }_{max}\approx 2$ and $K=1$, we obtain the first-order form of GCN [3]: (特别是，当 ${\lambda }_{max}\approx 2$且 $K=1$时，我们得到GCN[3]的一阶形式：)
  
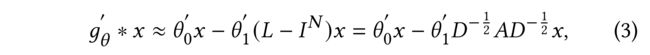
  • where free parameters ${\theta }_0^{\prime }$ and ${\theta }_1^{\prime }$ are shared over the whole graph. (自由参数${\theta }_0^{\prime }$ and ${\theta }_1^{\prime }$在整个图中共享。)
• (3) In effect, GCN constrains the number of parameters to prevent overfitting and normalizes the updated node vector to alleviate numerical instability problems (i.e. the renormalization trick $I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}⟶{\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}$, with $\hat{A}=A+I_N$ and ${\hat{D}}_{ii}={\sum }_j\widehat{A_{ij}}$). The final update function for GCN can be formulated as: (实际上，GCN限制参数的数量以防止过度拟合，并对更新的节点向量进行规范化以缓解 数值不稳定问题)
  
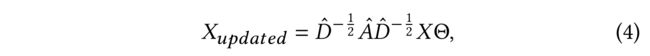
  • which can be regarded as an average on the embeddings of first-order neighbors and the central node. This can easily make nodes indistinguishable and thus cause the oversmoothing problem. (这可以看作是一阶邻居和中心节点嵌入的平均值。这很容易使节点难以区分，从而导致 过度平滑 问题。)

2.3 Graph Attention Network

• (1) Graph Attention Network [20] changes the operations of graph aggregation and combination in GCN to a weighted summation form by performing self-attention on each connected node pair. The weight between a center node $u$ and a neighbor node $s$ can be measured by: (图注意网络 [20]通过在每个连接的节点对上执行自我注意，将GCN中的图形聚合和组合操作更改为 加权求和 形式。中心节点$u$和邻居节点$s$之间的权重可以通过以下方式测量：)
  
  • where $sim$ is the similarity measure function, such as cosine similarity in most cases. (其中，$sim$是相似性度量函数，例如大多数情况下的余弦相似性。)
• (2) The coefficients are then normalized by softmax function to constrain the transformed value to avoid numerical instability problems: (然后，通过softmax函数对系数进行归一化，以约束转换后的值，以避免数值不稳定问题：)
  
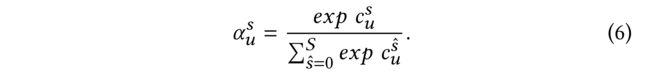
• (3) Then, the updated node embedding in a graph attention layer can be formulated as: (然后，嵌入在图注意层中的更新节点可以表示为)
  

2.4 Multi-channel Encoding Scheme

• (1) Graph Attention Network utilizes cosine similarity metric to measure the importance weight of the first order neighbors. More formally, given central user node $u$’s representation $X_u$ and one of its first-order neighbor node $s$’s representation $X_u^s$, the similarity score can be calculated as: ( 图注意网络 利用 余弦相似性度量 来度量一阶邻域的重要性权重。更正式地说，给定中央用户节点$u$的表示形式$X_u$和它的一阶邻居节点$s$的一个表示形式​$X_u^s$, 相似度得分可计算为：)
  

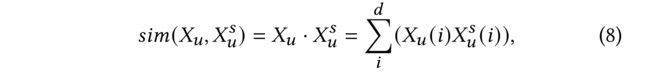
  • where $s$ denotes one of its neighbors ($s$表示它的一个邻居)
  • and $d$ is the number of dimensions or channels. ($d$是维度或通道的数量。)
  • After applying the above operation to all first-order neighbors, the similarity values of all neighbor nodes are normalized by softmax activation function to obtain the final node-wise linking weight. (将上述操作应用于所有一阶邻居后，通过softmax激活函数对所有邻居节点的相似性值进行归一化，以获得最终的 节点链接权重 。)

• (2) However, the method is computationally expensive due to multiple times of pairwise similarity computations. (然而，由于多次成对相似性计算，该方法的计算成本很高。)

  • For instance, for those nodes with hundreds of neighbors, the computational cost is unacceptable. (例如，对于具有数百个邻居的节点，计算成本是不可接受的。)
  • With channel-wise sparsity assumption, we could simplify GAT while modeling label-substructure relationships on the social network structure. (在通道稀疏性假设下，我们可以简化GAT，同时在社会网络结构上 建模标签子结构关系。)

• (3) When graph attention operations are performed on nodes of graph with sparse channel representations, pairwise node similarity can be approximated as: (当在具有稀疏通道表示的图的节点上执行图注意操作时，成对节点相似性可以近似为：)
  

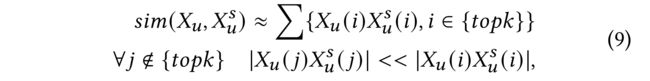
  • where the channels set $\{topk\}$ contains the channels with the largest element-wise multiplication values between $u$ and $s$. (通道集$\{topk\}$包含最大元素乘法值在$u$和$s$之间的通道。)

• (4) This approximation mainly depends on channel-wise sparsity between two adjoint nodes, (这种近似主要取决于两个伴随节点之间的 通道稀疏性，)

  • for example, when channel is sparse enough, the equation can be simplified into a single multiplication operation without summation parts. (例如，当通道足够稀疏时，方程可以简化为 一个乘法运算，而不需要求和部分。)

• (5) Under such circumstances, linking weight between user $u$ and $s$ can be approximated by: (在这种情况下，用户$u$和$s$之间的链接权重可以近似为：)
  

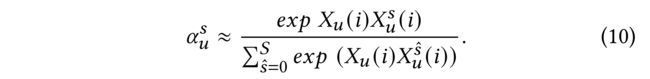
• (6)Then, the node-wise multiplication between nodes are simplified into element-wise multiplication , and weighted aggregation in GAT can be transformed into: (然后，将节点间的 节点 乘法简化为 元素 乘法，GAT中的加权聚合可以转化为：)
  

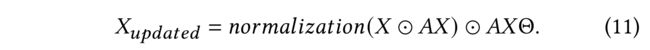
• (7) Note that the above normalization operation is performed in a channel-wise way while original graph attention mechanism realizes message computation, aggregation and update in a node-wise way. (注意，上述规一化操作是以通道方式执行的，而 原始的图形注意机制 以 节点方式 实现消息计算、聚合和更新。)

  • In essence, they have the same mathematical expression. (本质上，它们有相同的数学表达式。)
  • However, the channel-wise sparsity ensures that a few channels are sufficient for importance measurement, such that we can perform message computation after message aggregation instead of before it, which largely decreases the computational complexity of original GAT-based models. (然而，信道稀疏性确保了几个信道足以进行重要性度量，因此我们可以在消息聚合之后而不是之前执行消息计算，这大大降低了基于GAT的原始模型的计算复杂度。)
  • Besides, the equation can be regarded as controlling influence propagation on only some of the channels, which reflects partial relationships among users. (此外，该方程可被视为仅控制部分信道上的影响传播，这反映了用户之间的部分关系。)
  • In particular, it can be regarded as a chunk-based aggregation with chunk size 1, where only limited chunks (channels) transfer information. (特别是，它可以被视为块大小为1的基于块的聚合，其中只有有限的块（通道）传输信息。)
  • The framework of MEGCN is shown in Figure 2.
    
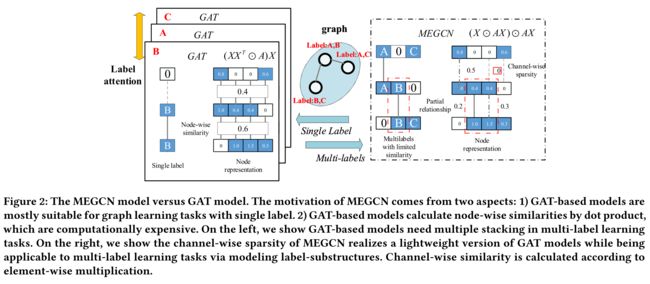
    图2:MEGCN模型与GAT模型。MEGCN的动机来自两个方面：1）基于GAT的模型主要适用于单标签的图形学习任务。2） 基于GAT的模型通过点积计算节点相似性，计算成本很高。在左边，我们展示了基于GAT的模型在多标签学习中需要多次叠加
    任务。在右边，我们展示了MEGCN的通道稀疏性实现了GAT模型的轻量级版本，同时通过建模标签子结构适用于多标签学习任务。根据元素乘法计算通道相似性。
    
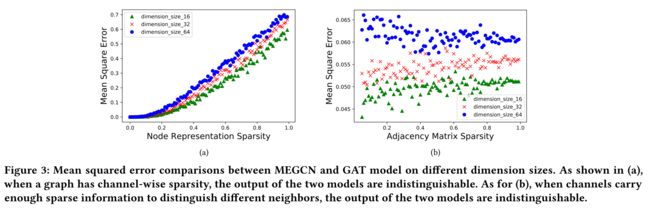
    图3:MEGCN和GAT模型在不同尺寸上的均方误差比较。如（a）所示，当一个图具有通道稀疏性时，两个模型的输出是不可区分的。至于（b），当信道携带足够的稀疏信息来区分不同的邻居时，两个模型的输出是不可区分的。

2.5 Sanity Check and Discussions

• (1) To show our model’s motivations, we test the channel-wise sparsity assumption on handcrafted datasets. (为了展示我们模型的动机，我们在手工制作的数据集上测试了 通道稀疏性假设)

  • First, we generate 100 nodes with each embedding dimension following normal Gaussian distribution. Without the loss of generality, the dimension size is set in the range [16, 32, 64]. (首先，我们生成100个节点，每个嵌入维度遵循 正态高斯分布 。在不丧失通用性的情况下，维度大小设置在[16,32,64]范围内。)
  • Then, we form the connected network structure by generating a random variable that follows the uniform distribution. As long as the value of the variable is larger than a sparse rate, which is defined as the percentage of non-zero dimensions of the original node embedding, we add a link between two nodes. (然后，我们通过生成服从均匀分布的随机变量来形成连通网络结构。只要变量的值大于稀疏率，即原始节点嵌入的非零维百分比，我们就在两个节点之间添加链接。)
  • Note that channel-wise sparsity in our work means sparsity along a few channels after element-wise multiplication of connected nodes embeddings. Therefore, it is hard to directly generate sparsity after multiplication operation. (注意，在我们的工作中，通道稀疏性是指在连接节点嵌入的元素相乘之后，沿着几个通道的稀疏性。因此，乘法运算后很难直接生成稀疏性。)
  • Instead, we use node representation sparsity to approximate channel-wise sparsity. (相反，我们使用 节点表示稀疏性 来近似 信道稀疏性。)
  • In particular, we test the effects of different node representation sparsity and adjacency matrix sparsity to show how they affect the results. (特别是，我们测试了不同 节点表示稀疏性 和 邻接矩阵稀疏性 的影响，以显示它们如何影响结果。)

• (2) As shown in Figure 3(a) , the mean squared error difference between MEGCN output and GAT output with the same sparse node representation is minimal when node sparsity percentage is very low. (如图3(a)所示，当节点稀疏度百分比非常低时，具有相同稀疏节点表示的MEGCN输出和GAT输出之间的 均方误差差 最小。)

  • The graph and node embeddings are generated with adjacency matrix sparsity of 0.2, and each node has around 20 neighbors. (图和节点嵌入是在 邻接矩阵稀疏度为0.2的情况下生成的，每个节点大约有20个邻居。)
  • As for the number of neighbors, when the number of linking channels in each pair is larger than the number of neighbors, GAT and MEGCN achieve the similar performance. The results are shown in Figure 3(b) with node representation sparsity rate of 0.2. (至于邻域数，当每对中的链接通道数大于邻域数时，GAT和MEGCN的性能相似。结果如图3（b）所示，节点表示稀疏率为0.2。)
  • However, in most cases, the number of channels can be far less than the number of neighbors, which makes it hard to distinguish node in each channel. In response, we could use neighborhood sampling techniques to help limit the channel-wise information confusion. (然而，在大多数情况下，通道的数量可能远远少于邻居的数量，这使得很难区分每个通道中的节点。作为回应，我们可以使用 邻域采样技术 来帮助 限制通道信息混乱 。)

• (3) To this end, we could adopt the same ideas on the social network-based recommendation system, which is a multi-label learning task with extreme label sparsity. (为此，我们可以在基于社交网络的推荐系统上采用相同的想法，这是一个具有 极端标签稀疏性 的 多标签学习任务。)

  • The label-substructures induce the partial relationships among users in the original social network. (标签子结构诱导了原始社交网络中用户之间的 部分关系。)
  • We need develop extra some normalization approaches to ensure the channel-wise sparsity such that personal interests and shared interests can simultaneously propagate along the sparsity channels. (我们需要开发一些额外的规范化方法来确保 通道的稀疏性，这样个人兴趣和共享兴趣可以同时沿着稀疏通道传播。)
  • We hope the normalization function in Eq. (11) can generate sparse channel links, which requires normalization functions shrink most channel values to zeros while enlarging the non-zero ones. Hence, the equation can generate a sparse update on user representation and further lead to channel-wise sparsity. (我们希望公式（11）中的归一化函数能够生成稀疏信道链路，这要求归一化函数将大多数信道值收缩为零，同时放大非零信道值。因此，该方程可以生成用户表示的稀疏更新，并进一步导致 信道稀疏性。)
  • In general, softmax function is regarded as useful normalization function. (通常，softmax函数被认为是有用的归一化函数。)
  • However, after updating a user’s representation, values among channels will be imbalanced due to the nonlinear normalization nature of softmax function. As a result, it can further lead to gradient explosion or vanishing on some linking channels, as well as overfitting problems. (然而，在更新用户表示后，由于softmax函数的非线性归一化性质，信道之间的值将不平衡。因此，它可能会进一步导致某些连接通道上的 梯度爆炸或消失 ，以及 过拟合问题。)
  • Therefore, we should normalize the values in each channel of the node representation after each update step. (因此，我们应该在每个更新步骤之后规范化节点表示的每个通道中的值。)

3 THE PROPOSED MODEL

图4：提出模型的说明。左侧子图显示了整个模型框架，右侧子图显示了影响扩散过程中的MEGCN。特别是对于MEGCN，稀疏影响被用来转换多信道影响和用户的信道稀疏性。需要注意的是，规范化掩码可以被视为社交网络上的一种兴趣分离，以模拟部分关系，它将社交网络划分为每个通道中具有稀疏链接的兴趣子结构。特别是，MEGCN通过元素级产品操作捕获多通道特征相似性。影响力管理的提出是为了保证社会影响力的稀疏性。此外，ChannelNorm设计用于平衡通道值，从而防止数值问题，并增加节点区分，以缓解过平滑问题。

3.1 Model Framework

• We introduce MEGCN into the social recommend system and the overall framework is shown in Figure 4. The model is composed of five Layers: Embedding Layer, Fusion Layer, User Action Aggregating Layer, Influence Diffusion Layer, Prediction Layer. We detail each parts as follows: (我们将MEGCN引入社交推荐系统，总体框架如图4所示。该模型由五层组成：嵌入层、融合层、用户行为聚合层、影响扩散层、预测层。我们对每个部分的详细说明如下：)

3.1.1 Embedding Layer.

• (1) For each user or item, the original discrete one-hot encoding generates extreme feature sparsity. (对于每个用户或项目，**原始的离散one-hot编码会产生 极端的特征稀疏性。)
• (2) Hence, we use an embedding layer to encode users and items with corresponding continuous values. Formally, given the one-hot representations of a user or an item, the embedding layer performs an index operation on free user embedding matrix $X$ or item embedding matrix $Y$. For instance, user $a$’s free latent embedding is obtained as: (因此，我们使用嵌入层用相应的连续值对用户和项目进行编码。形式上，给定用户或项目的 one-hot表示 ，嵌入层对 自由用户嵌入矩阵$X$或 项目嵌入矩阵$Y$执行 索引操作 。例如，用户$a$的自由潜在嵌入如下所示：)
  

3.1.2 Fusion Layer.

• (1) Besides free embedding, items and users have their associated side information, e.g. text description, which can be regarded as feature embedding. (除了自由嵌入外，项目和用户还有相关的 辅助信息 ，例如文本描述，这可以被视为 特征嵌入。)
• (2) Fusion layer takes free embedding $X$, $Y$ ($X_a$ for user $a$ or $Y_i$ for item $i$) and features embedding $P$, $Q$ ($P_a$ for user $a$ or $Q_i$ for item $i$) as input, and outputs an initial user fusion embedding $h_a^0$ or an item fusion embedding $v_i$ via a fully connected neural network. For instance, the initial fusion embedding for user $a$ is calculated as: (Fusion layer以自由嵌入$X$、$Y$（$X_a$用于用户$a$或$Y_i$用于项目$i$）和嵌入$P$、$Q$（$P_a$用于用户$a$或$Q_i$用于项目$i$）为输入，并通过 一个完全连接的神经网络 输出初始用户融合嵌入$h_a^0$或项目融合嵌入$v_i$。例如，用户$a$的初始融合嵌入计算如下：)
  
  • where $W$ and $b$ are the parameters that need to be learned, ($W$和$b$是需要学习的参数，)
  • and $\sigma$ is the activation function. ($\sigma$是激活函数。)
• (3) Obviously, by setting $W$ and $b$ as an identity matrix and zero vector, respectively, we could simplify the fusion layer into a concatenation operation. Similarly, we can obtain the item fusion embedding $v_i$ for item $i$. (显然，通过将$W$和$b$分别设置为单位矩阵和零向量，我们可以将融合层简化为串联操作。类似地，我们可以为$i$项获得$v_i$项。)

3.1.3 User Action Aggregating Layer.

• (1) We capture a user’s behavior encoding by mean pooling on the fusion embedding of items the user has interacted with in the past. Note that the method was firstly proposed in SVD++ [10]. For instance, we obtain user $a$’s behavior encoding $w_a$ by: (我们通过对用户过去交互过的项目进行融合嵌入，通过平均池化 来捕获用户的行为编码。请注意，该方法最初是在 SVD++ [10]中提出的。例如，我们通过以下方式获得 用户$a$的行为编码$w_a$：)
  
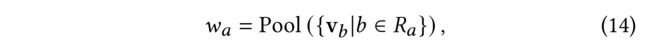
  • where $v_b$ is the item fusion vector for item $b$ in user action history $R_a$, ($v_b$是用户操作历史$R_a$中$b$项的项融合向量，)
  • and $w_a$ denotes behavior encoding of user $a$ learned from history actions. ($w_a$表示用户$a$从历史动作中学习到的行为编码。)

3.1.4 Influence Diffusion Layer.

• (1) By feeding user interest into the influence diffusion layer, we model the propagation dynamics of users’ interest in social network $S$. (通过将用户兴趣输入影响扩散层，我们对社交网络$S$中用户兴趣的动态传播进行建模 )
  • For each user $a$, we use $h_a^k$ to represent interest after $k$ hops of dynamic influence diffusion in the social network. (对于每个用户$a$，我们使用$h_a^k$表示在社交网络中进行$k$次动态影响扩散后的兴趣。)
  • Each diffusion layer contains three operations: (每个扩散层包含三个操作：)
    • selecting neighbors to diffuse information, (选择邻居去传播信息，)
    • aggregating neighbor influence （聚合邻居的影响）
    • and combining self interest with neighbors’ influence [30]. (将自身兴趣与邻居的影响结合起来)
  • To capture partial relationships among users in the social network, we propose MEGCN in the information diffusion process. (为了捕捉社交网络中用户之间的部分关系，我们在信息扩散过程中提出了MEGCN。)
  • In MEGCN, we use channel-wise similarity to measure the importance of social influence in each channel from a neighbor. (在MEGCN中，我们使用 通道相似性 来衡量邻居在每个渠道中的社会影响力的重要性。)
  • Each dimension of $h_a$ can be regarded as a channel of an independent interest. ($h_a$的每个维度​可以看作是一个独立兴趣的通道。) 这篇文章的着力点
  • For instance, the interest of color and shape could be stored in the first and second channel respectively. (例如，颜色和形状的兴趣可以分别存储在第一和第二通道中。)
  • Besides, we assume users’ interests on some channels are inherently stable, which means users will selectively absorb information from neighbors with partial relationships. (此外，我们假设用户在某些渠道上的兴趣本质上是稳定的，这意味着用户会有选择地从部分关系的邻居那里吸收信息。)
  • Therefore, with sparse channel representation, we could capture interest similarity on different channels between connected nodes. The proposed model puts the message computation part after message aggregation part instead of before it in other GNN models. (因此，通过稀疏信道表示，我们可以捕获连接节点之间不同信道上的兴趣相似性。在其他GNN模型中，该模型将消息计算部分放在消息聚合部分之后，而不是放在消息计算部分之前。)

3.1.4.1 Aggregating

• The model can be regarded as a subgraph information diffusion on each channel, where nodes distinguish from each other by controlling the sparse linking rate. (该模型可以看作是 每个通道上 的子图信息扩散，其中节点通过控制稀疏链接速率来区分彼此。)
• We perform a linear transformation on aggregated information from neighbors $\tilde{a}$ in user’s ego network $S_a$ to obtain neighbor influence vector $c^k$: (我们对来自用户自己网络$S_a$中邻居$\tilde{a}$的聚合信息执行 线性变换，以获得 邻居影响向量$c^k$：)
  

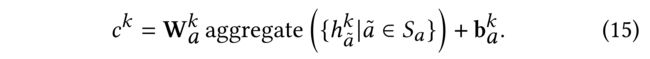
3.1.4.2 InfluenceNorm

• (1) InfluenceNorm first conducts elemen-twise multiplication to identify important channels from the neighborhood influence vector. (InfluenceNorm首先执行elemen twise乘法，从邻域影响向量中识别重要通道。)
• (2) Then, after normalization, InfluenceNorm generates a sparse channel-wise mask that determines importance weight of each channel in different label-substructure relations. (然后，在标准化之后，InfluenceForm生成一个 稀疏的通道掩码 ，该掩码确定不同标签子结构关系中每个通道的重要性权重。)
• (3) In effect, inspired by graph attention network, which uses softmax to normalize the importance weight between each node pair, we use softmax as the normalization function. The sparse influence is computed as: (实际上，受图形注意网络(该网络使用softmax规范化每个节点对之间的重要性权重)的启发，我们使用softmax作为规范化函数。稀疏影响的计算公式为：)
  
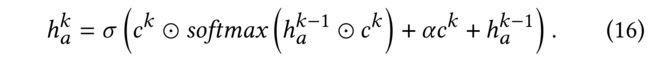
• (4) We add a residual part $a{c}^k$ to avoid gradient vanishing problem and a hyperparameter $\alpha$ to control the weight. (我们添加了一个残差部分$a{c}^k$以避免 梯度消失 问题，和一个超参数$\alpha$来控制权重。)

3.1.4.3 ChannelNorm

• (1) After performing softmax operation in InfluenceNorm, we obtain node embeddings with highly imbalanced channel values. (在InfluenceNorm中执行softmax操作后，我们获得了 通道值高度不平衡 的节点嵌入。)
• (2) Hence, the model may face numerically unstable problems in some channels, which will lead to a local minimum. (因此，该模型在某些通道中可能面临 数值不稳定 问题，这将导致局部极小值。)
• Meanwhile, channel-wise sparsity will divide the original social network into multi-channel label-substructures, (同时，通道稀疏性 将原始社会网络划分为 多渠道标签子结构)
  • i.e. partial relationships, which can be better modeled with a larger substructure diversity or channel-wise distinction. (例如.部分关系，可以用更大的子结构多样性或通道差异更好地建模。)
• (3) Hence, we adopt the ideas from PairNorm [41] to control the value imbalance between channels, and propose ChannelNorm: (因此，我们采用PairNorm[41]的思想来控制通道之间的价值不平衡，并提出了 ChannelNorm)
  
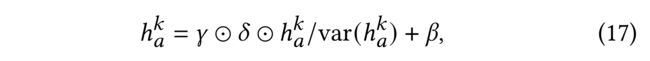
  • where $\gamma$ and $\beta$ represent trainable channel-wise scale and shift vectors in ChannelNorm operation, (表示ChannelNorm操作中 可训练的通道尺度 和 移位向量，)
  • and $\delta$ is the hyperparameter that controls the normalized variance. (是控制标准化方差的超参数。)
• (4) We add such parameters for a better channel-wise distinction. After updating sparse influence with ChannelNorm, users preserve their own interests while accepting sparse influence from neighbors, which can preserve necessary distinction between each node pair, thus alleviating the oversmoothing problem. (我们添加这些参数是为了更好地区分通道。在使用ChannelNorm更新稀疏影响后，用户在接受邻居的稀疏影响的同时保留了自己的兴趣，这可以在每个节点对之间保留必要的区别，从而缓解 过度平滑 问题。)

3.1.5 Prediction Layer.

• After $K$ hops of social influence propagation, we obtain each user’s final embedding by combining information via influence diffusion and user action aggregating. The final predicted rating is measured by the multiplication of the two latent vectors. (在社交影响传播的$K$跳之后，我们通过影响扩散和用户行为聚合来组合信息，从而获得每个用户的最终嵌入。最终的预测评级通过两个潜在向量的乘积来衡量。)
  

3.1.6 Loss Function.

• We use the same pair-wise ranking-based loss function in [16, 30]: (我们在[16,30]中使用了相同的 基于成对排序的损失函数 ：)
  
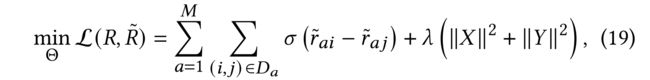
  • where $D_a=\{(i,j)|i\in R_a\wedge j\in V-R_a\}$ denotes the pairwise training data for user $a$ with user history action set $R_a$ (表示用户$a$和用户历史操作集$R_a$的成对训练数据)
  • and $\sigma (x)$ is the sigmoid function,

3.2 Training

• In this section, we introduce some implementation details in the model training part. (在本节中，我们将在模型培训部分介绍一些实现细节。)

3.2.1 Mini-Batch Training.

• In practice, to avoid huge computational consumption, we divide training data into batches following the procedure that each user’s training records are ensured in the same mini-batch, which helps avoid the repeated computation of each user a’s latent embedding $h_a^k$ in the iterative influence diffusion layers [30]. For every epoch, we shuffle the training set to generate different batches. (在实践中，为了避免巨大的计算消耗，我们按照确保每个用户的训练记录在同一个小批量中的过程将训练数据分成多个批次，这有助于避免重复计算每个用户a的潜在嵌入$h_a^k$在 迭代影响扩散层中[30]。对于每个时代，我们都会对训练集进行打乱，以生成不同的批次。)

3.2.2 Negative Sampling.

• Since we only observe positive feedbacks in the original two datasets, we use the negative sampling technique to obtain pseudo negative feedbacks at each iteration in the training process, with the assumption that all items without implicit feedbacks in training data will have equal probability to be selected as a negative sample. (由于我们只在原始的两个数据集中观察到正反馈，我们使用 负采样技术 在训练过程中的每次迭代中获得 伪负反馈 ， 假设所有在训练数据中没有隐含反馈的项目被选为负样本的概率相等。)

3.2.3 Dropout and Regularization.

• Since the MEGCN uses sparse influence to update users’ interest, the model can easily run into a local minima. (由于MEGCN使用稀疏影响来更新用户的兴趣，因此该模型很容易陷入局部极小值)
• Hence, we use feature-wise dropout between different diffusion layers. (因此，我们在不同的扩散层之间使用 基于特征的dropout。)
• To reduce the effects of channel information mixture when the number of neighbors is huge, we also apply dropout on adjacency matrix, which can be regarded as a sampling among neighbors, such that users update their interests based on a subset of neighbors. (为了减少邻居数量巨大时信道信息混合的影响，我们还对邻接矩阵应用了dropout，邻接矩阵可以被视为邻居之间的抽样，这样用户可以根据邻居的子集更新兴趣。)
• As for the regularization, we use L2-regularization on both user and item embeddings with the same regularization rate. (对于正则化，我们在用户和项目嵌入上使用L2正则化，并且正则化率相同。)

3.3 Discussion

3.3.1 Time Complexity Analysis.

• (1) Compared with traditional recommendation models, the main additional time costs of the social recommendations occur in the layer-wise influence diffusion process. (与传统的推荐模型相比，社会推荐的额外时间成本主要发生在 分层影响扩散过程中。)
• (2) More specifically, linear transform operation in GCN only costs $O(MK{d}^2)$, (更具体地说，GCN中的线性变换操作只需花费$O(MK{d}^2)$，)
  • where $M$ is the number of users in graph, ($M$是图中的用户数)
  • $K$ is the step of influence diffusion, ($K$是影响力扩散的步数)
  • and $d$ is the length of features or channels. ($d$是特征或通道的长度。)
• (3) MEGCN uses sparse influence to capture multi-channel distinction between social influence and self interests, which costs an additional time complexity $O(MKd)$ compared with GCN . ( MEGCN使用 稀疏影响 来捕捉社会影响和个人兴趣之间的 多通道区别 ，与 GCN 相比，这需要额外的时间复杂度 $O（MKd）$。)
• However, GAT needs to computs an attention score between each pair of connected nodes, thus it is the most time consuming algorithm with computational complexity $O(M^{2}K{d}^2)$ in full version and $O(MNK{d}^2)$ in sparse version ($N$ denotes links number), which is around ten times larger than other models. (然而，GAT需要计算每对连接节点之间的注意分数，因此它是最耗时的算法，完整版本的计算复杂度为$O(M^{2}K{d}^2)$,稀疏版本的计算复杂度为$O(MNK{d}^2)$（$N$表示链路数），大约是其他模型的十倍。)

4 EXPERIMENTS

• In this section, we evaluate our methods via the experiments on two real-world recommendation tasks. (在本节中，我们通过在两个实际推荐任务上的实验来评估我们的方法。)

4.1 Data Preparation

• We evaluate the performance of our model on two recommendation datasets with social network: Yelp and Flickr. (我们在两个具有社交网络的推荐数据集：Yelp和Flickr上评估了我们的模型的性能。)
• These two datasets are provided in DiffNet [30] and have been explained in detail. (DiffNet[30]中提供了这两个数据集，并对其进行了详细解释。)
• In the data preparation step, we filter out users with less than 2 historical action records and 2 social neighbors in both datasets. (在数据准备阶段，我们筛选出两个数据集中历史动作记录和社交邻居少于2个的用户。)
• Then the datasets for experiments are built as follows. We randomly divide 10% of datasets as test set, 10% as validation set, and the rest 80% as the training set. The detail statistics of the two datasets after preprocessing are shown in Table 1. (然后，实验数据集如下所示。我们随机将10%的数据集划分为测试集，10%为验证集，其余80%为训练集。预处理后的两个数据集的详细统计数据如表1所示。)
  

4.2 Baselines

Since the social recommendation task involves social networks, we compare MEGCN with various state-of-the-art social network-based graph neural networks: (由于社交推荐任务涉及社交网络，我们将MEGCN与各种最先进的基于社交网络的图形神经网络进行比较：)

• SVD++ [13]. SVD++ only utilizes user-item interaction graph without any other side information, and it can be seen as the baseline model for recommendation systems without social networks. (SVD++只利用用户项交互图，没有任何其他方面的信息，可以看作是没有社交网络的推荐系统的基线模型。)
• TrustSVD [10]. TrustSVD is the first model to use social network on recommendation systems. The model only aggregates one hop neighborhood information without other similarity assumption. (TrustSVD是第一个在推荐系统中使用社交网络的模型。该模型只聚合一跳邻域信息，没有其他相似性假设。)
• DiffNet [30]. Compared with TrustSVD, DiffNet incorporates multi-hop dynamic diffusion layers. The method uses first-order approximation of graph spectral network.
• GCN [3]. Compared with Diffnet, GCN adds a renormalization trick on the aggregating operation. (与Diffnet相比，GCN在聚合操作上增加了一个重归一化技巧。)
• GAT [20]. GAT leverages an attention layer to calculate the correlation score between two neighbor nodes and sets it as the rate of information aggregation. (GAT利用注意层计算两个相邻节点之间的相关性得分，并将其设置为信息聚合速率。)
• DualGAT [31]. DualGAT extends social effects from user domain to item domain and leverages dual graph attention mechanism to collaboratively learn representations for static and dynamic social effects. Similar works can be found in [29] and [7]. In essence, their work can model item (label)-substructure by incorporating user-item interactions in the information diffusion process of the social network. Other works [42, 43] that utilize attention mechanism without social network effects are not shown in our experiments. (DualGAT将社会效果从用户域扩展到项目域，并利用双图注意机制协作学习 静态 和 动态 社会效果的表示。类似的作品可以在[29]和[7]中找到。本质上，他们的工作可以通过在社交网络的信息扩散过程中加入用户项目交互来模拟项目（标签）子结构。我们的实验中没有展示其他利用注意机制而没有社交网络效应的作品[42,43]。)

4.3 Evaluation Metrics

As our work focuses on recommending top-N items, we use two ranking-based evaluation metrics, which are Hit Ratio (HR) and Normalized Discounted Cumulative Gain (NDCG). The two metrics are defined as: (由于我们的工作重点是推荐排名前N的项目，我们使用了两个基于排名的评估指标，即命中率（HR）和标准化贴现累积收益（NDCG）。这两个指标定义为：)

4.3.1 Hit Ratio

• measures the number of items that the user likes n the test data that has been successfully predicted in the top-N ranking list. It can be given as: (测量用户喜欢的项的数量n在前n个排名列表中成功预测的测试数据。可给出如下公式：)
  

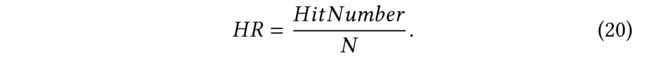
4.3.2 Normalized Discounted Cumulative Gain

• considers the hit positions of the items and gives a higher score if the hit items in the top positions [19]. (考虑项目的命中位置，如果命中项目位于顶部位置，则会给出更高的分数[19])
  

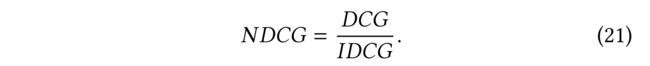
4.4 Results Summary

4.4.1 Parameter Setting.

• For all the models that are based on the latent factor models, we initialize the latent vectors with small random values. (对于所有基于潜在因子模型的模型，我们用小的随机值初始化潜在向量。)
• In the model learning process, we use Adam as the optimizing method for gradient descent based methods with an initial learning rate of 0.001. (在模型学习过程中，我们使用Adam作为基于梯度下降的方法的优化方法，初始学习率为0.001。)
• And the batch size is set as 512.
• For the parameter settings, we set the embedding dimension size as 64.
• Moreover, we adjust some baseline models to make sure all the models have consistent embedding dimensions.
• In our model, there are four hyperparameters to be fine-tuned.
• Learning rate $lr$ is selected from $[1e-1,1e-2,1e-3,1e-4,1e-5]$,
• normalization variance $\delta$ is searched in the range of [1,2,4,8],
• l2 normalization rate $\lambda$ is selected from $[1e-2,2e-2,3e-2,4e-2]$,
• and residual rate $\alpha$ is searched in the range of [0.1,0.2,0.3,0.4,0.5].
• We fine-tune those hyperparameters to get the best results on validation set.
• The values of two metrics in the test datasets are obtained after 400 epochs.

4.4.2 Overall Comparison.

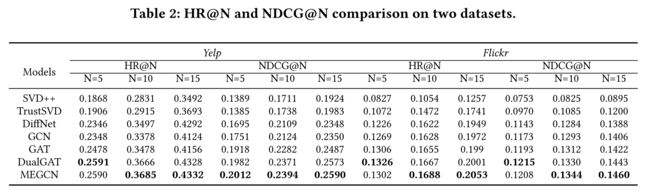
• (1) Table 2 compares the average HR and NDCG of the benchmarks with our MEGCN model. (表2比较了基准的平均HR和NDCG与我们的MEGCN模型。)
• (2) First, we can observe that our model outperforms others in all two datasets, which indicates that channel-wise sparsity-based model performs better than traditional graph attention models. (首先，我们可以观察到，我们的模型在所有两个数据集中都优于其他模型，这表明基于通道稀疏性的模型比传统的图形注意模型表现更好。)
• (3) Second, the performance of GCN is better than DiffNet in most cases, which indicates that the stacking of layers with more parameters can enhance the performance of the model. (第二，在大多数情况下，GCN的性能优于DiffNet，这表明具有更多参数的层的叠加可以提高模型的性能。)
• (4) Third, we find GAT models outperform other Laplacian Smoothing-based models, which proves the importance of distinguishing different neighbors. (第三，我们发现GAT模型优于其他基于拉普拉斯平滑的模型，这证明了区分不同邻域的重要性。)
• In addition, dualGAT achieves the best performance among baseline models since it considers both static and dynamic social influence. (此外，dualGAT在基线模型中表现最好，因为它同时考虑了 静态和动态社会影响 。)
  

4.4.3 Partial Relationship Analysis.

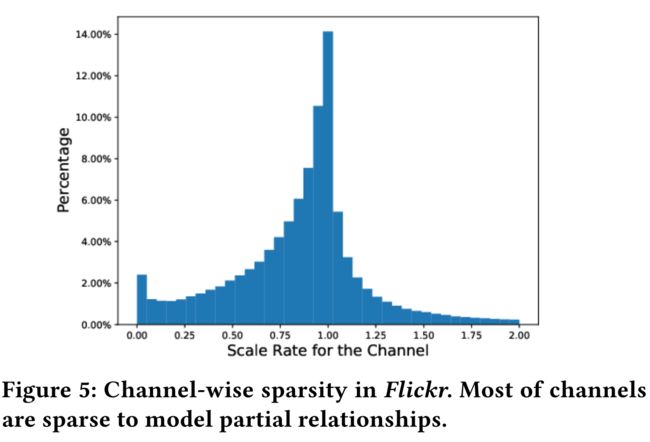
• To find out how channel-wise sparsity in MEGCN helps improve model performance, we conduct extra experiments using Flickr dataset. (为了了解MEGCN中的通道稀疏性如何帮助提高模型性能，我们使用Flickr数据集进行了额外的实验。)
• We obtain users’ representations after two hops of influence diffusion based on our model. (基于我们的模型，我们在两跳影响扩散后获得用户的表示。)
• As shown in Figure 5, about 30% of channels perform like GCN with scale weight around 1, and the others are typical MEGCN outputs with sparse influence update. (如图5所示，大约30%的通道的性能类似于GCN，标度权重约为1，其他通道是典型的MEGCN输出，具有稀疏影响更新。)
• Based on our assumption in equation 10, they model partial relationships with enough channel-wise sparsity. (基于我们在等式10中的假设，它们以足够的信道稀疏性来模拟部分关系。)
• As a result, MEGCN assigns different weights to different channels for a better recommendation performance. (因此，MEGCN为不同的渠道分配不同的权重，以获得更好的推荐性能)
  

4.4.4 Oversmoothing Problem.

• (1) We compare models performance after multi-hop influence diffusion. (我们比较了多跳影响扩散后模型的性能。)
• (2) One of the disadvantages of GCN models is the oversmoothing problem, which refers to the phenomenon that as nodes dynamically aggregate information from their neighbors, nodes will become similar with each other after multiple hops of diffusion. (GCN模型的缺点之一是 过度平滑 问题，它指的是当节点动态地聚集来自其邻居的信息时，节点在经过多跳扩散后会变得彼此相似的现象。)
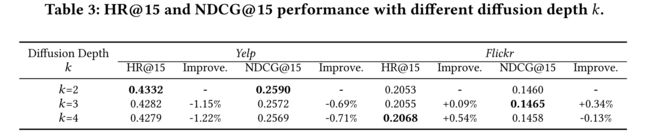
• (3) We test our model with three ascending diffusion depths, which are shown to have increasingly negative effects on recommendation performance in [1]. Nevertheless, as illustrated in Table 3, our model can achieve consistent prediction performance even after many hops of information aggregation, which shows that our model can alleviate oversmoothing problem in the dynamic influence diffusion process with InfluenceNorm and ChannelNorm. (我们用三个上升的扩散深度来测试我们的模型，在[1]中，这三个扩散深度对推荐性能的负面影响越来越大。然而，如表3所示，我们的模型即使在多次信息聚合之后也能实现一致的预测性能，这表明我们的模型可以缓解带有InfluenceNorm和ChannelNorm的动态影响扩散过程中的过度平滑问题。)
• (4) In sum, the model can separate multi-channel interests in the social influence context. (总之，该模型可以在社会影响背景下分离多渠道利益。)

4.4.5 Time Cost and Channel Independence.

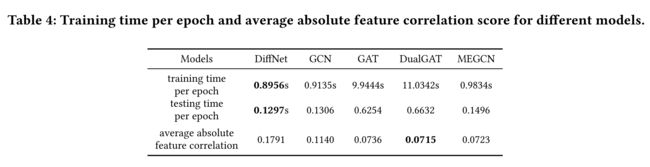
• We list the feature correlation scores and training/testing time costs for different models in Table 4. (我们在表4中列出了不同模型的特征相关分数和培训/测试时间成本。)
• On one hand, we can observe that MEGCN achieves around 10 times computational efficiency compared with advanced attention-based GNN models, such as GAT and DualGAT, while generating a similar lower correlation score. It indicates MEGCN better models partial relationship in different channels. (一方面，我们可以观察到，与先进的基于注意的GNN模型（如GAT和DualGAT）相比，MEGCN的计算效率大约是后者的10倍，同时产生了类似的较低的相关分数。这表明MEGCN能更好地模拟不同渠道的部分关系。)
• On the other hand, it displays similar time costs compared with traditional GCN models. (另一方面，它显示出与传统GCN模型类似的时间成本。)
• In particular, the feature-wise correlation matrix of user interests generated by DiffNet and MEGCN are shown in Figure 6. The lighter color heatmap directly shows the lower correlation score between features via MEGCN model. (特别是，DiffNet和MEGCN生成的用户兴趣特征相关矩阵如图6所示。通过MEGCN模型，浅色热图直接显示了特征之间较低的相关性得分。)
• Better channel independence stands for a more reliable partial relationship. (更好的渠道独立性意味着更可靠的部分关系。)
• Both MEGCN and DualGAT achieve a good performance on such metric, which indicate that MEGCN can model partial relationship like GAT-based models. (MEGCN和DualGAT在这种度量上都取得了很好的性能，这表明MEGCN可以像基于GAT的模型一样建模部分关系。)

5 RELATED WORK

5.1 Social Recommendation

• Social effects have been widely exploited in recommendation systems to solve data sparsity problems. (在推荐系统中，社会效应被广泛用于解决 数据稀疏 问题。)
• Fundamentally, current studies can be divided into similarity-based methods and model-based methods. (从根本上讲，目前的研究可以分为 基于相似性 的方法和 基于模型 的方法。)
• Especially, most current methods leverage deep neural networks [2, 6, 21, 26, 30, 39] to capture nonlinear information. (尤其是，目前大多数方法都利用 深度神经网络 [2,6,21,26,30,39]来捕捉非线性信息。)
• However, they either assume social influence dominates the user behavior or are too computationally expensive. Note that, besides direct social effects, various peer relations [24, 34] can be contructed to improve representation learning and recommendation performance. (然而，他们要么认为社会影响主导了用户行为，要么计算成本太高。请注意，除了直接的社会影响外，还可以构建各种 同伴关系 [24,34]，以提高表征学习和推荐表现。)

5.2 Graph Neural Networks

• (1) Traditional graph embedding methods [8, 9, 17] and original Graph Convolution Network [3] mainly focus on embedding nodes from a single fixed graph, thus lacking the ability to generalize to unseen nodes. (传统的 图嵌入 方法[8,9,17]和原始 图卷积网络 [3]主要关注于从单个固定图中嵌入节点，因此缺乏推广到不可见节点的能力。)
• (2) Then, [11, 22, 36] proposed to aggregate graph information in an inductive way, and the dynamic structure and feature information aggregation mechanism have helped achieve impressive performance in graph-involved tasks. (然后，[11,22,36]提出以 归纳的方式 聚合图形信息，动态结构 和 特征信息聚合机制 有助于在涉及图形的任务中获得令人印象深刻的性能。)
• (3) However, in essence, Graph Convolution Network is a special form of Laplace Smoothing [14], which is a spectrum method that constrains neighborhood to be similar. Therefore, it is not appropriate to directly utilize GCN and its variants [11, 36] directly in social recommendation task since they tend to attach equal importance weights to neighbors. (然而，在本质上，图卷积网络 是 拉普拉斯平滑 的一种特殊形式[14]，这是一种 *频谱方法，限制邻域相似 。因此，在社会推荐任务中直接使用GCN及其变体[11,36]是不合适的，因为它们 倾向于对邻居同等重视。)
• (4) One possible solution is to utilize graph attention network [20] as it can learn the latent embeddings of each node by attending to its neighbors following a self-attention strategy. (一种可能的解决方案是利用 图注意网络[20]，因为它可以通过遵循 自我注意策略 关注其邻居来学习每个节点的 潜在嵌入 。)
• Nevertheless, it is computationally expensive in large scale networks. (然而，在大规模网络中，它的计算成本很高。)
• Besides, various works have proposed to leverage substructures [22, 23, 25] information in graph-based learning models. (此外，各种研究已经提出在基于图的学习模型中利用 子结构 [22,23,25]信息。)
  

5.3 Multi-label Learning

• (1) Multi-label learning [40] has been widely applied to different machine learning tasks, such as text categorization [15, 18], image annotation [27]. (多标签学习[40]已广泛应用于不同的机器学习任务，如 文本分类 [15,18]， 图像注释 [27]。)
• (2) However, in most cases, a multi-label learning task faces empty relevant label problem [32] and then model performance can be largely affected when incomplete multi-labels are used for learning. (然而，在大多数情况下，多标签学习任务面临 空相关标签问题 [32]，当使用不完整的多标签进行学习时，模型性能会受到很大影响。)
• (3) [5] proposes to handle such problems by learning from semi-supervised weak-label data. ([5] 提出了利用 半监督弱标签数据 来处理这类问题。)
• (4) Inspired by [5], since graph-based models are typical semi-supervised, multi-task learning can be realized according to graph-based models. [37] is one of the earliest works applying multi-label learning on recommendation tasks. (受[5]的启发，由于基于图的模型是典型的半监督模型，因此可以根据基于图的模型实现多任务学习。[37]是最早将多标签学习应用于推荐任务的著作之一。)

6 CONCLUSION

• (1) In this paper, we propose MEGCN, a graph neural network based on channel-wise sparsity. (本文提出了一种基于 信道稀疏性 的图神经网络MEGCN。)

• (2) MEGCN simplifies GAT operation and utilizes two models, InfluenceNorm and ChannelNorm, to capture both self interest and shared interest in the influence diffusion process of social recommendation task. (MEGCN简化了GAT的操作，并利用两种模型，即InfluenceNorm和ChannelNorm，在社会推荐任务的影响扩散过程中捕获了 个人兴趣 和 共享兴趣 。)

• (3) Essentially, our work can model the sparse label-induced structures in the original social network, namely partial relationship, without suffering from expensive computational cost of graph attention based models. (本质上，我们的工作可以对原始社会网络中的稀疏标签诱导结构（即部分关系）进行建模，而不必承受基于图形注意模型的昂贵计算成本。)

• (4) Finally, experimental results validate the effectiveness of the proposed models. In particular, the MEGCN achieves the highest HR and NDCG score on all datasets. (最后，实验结果验证了所提模型的有效性。特别是，MEGCN在所有数据集上的HR和NDCG得分最高。)

• (1) Future research will be conducted from both theoretical and practical perspectives. Theoretically, we will explore how to further improve the performance of the MEGCN models from the optimization point of view. (未来的研究将从理论和实践两个角度进行。理论上，我们将从优化的角度探讨如何进一步提高MEGCN模型的性能。)

• (2) Besides, since graph sub-structure has been validated to be useful for graph modeling [22, 25], we will explore the usefulness of such information in the social recommendation task. (此外，由于图的子结构已被证实对图建模有用[22,25]，我们将探讨这些信息在社会推荐任务中的有用性。)

• (3) In practice, we will apply the method to other graph-based multi-label tasks and test whether it it applicable for all kinds of tasks. (在实践中，我们将把该方法应用于其他基于图的多标签任务，并测试它是否适用于所有类型的任务。)

ACKNOWLEDGMENTS

REFERENCES