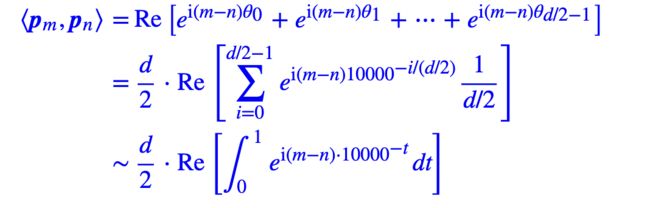Transformer 代码+原理
文章目录
- reference
- 总览
- 详述
-
- self-attention
-
- 为什么要除以 d k \sqrt{d_k} dk
- 多头注意力机制
- feed forword
- 残差连接
- 编码器
- 解码器
- 线性层和softmax
- 输入层
-
- 为什么要这么设计位置编码
reference
The Illustrated Transformer
图解transformer
总览
首先,将transformer视为黑匣子,在机器翻译任务中,输入A语言的句子,输出B语言对应的翻译:

transformer由encoders和decoders两部分组成,且encoders与decoders都是由多个encoder/decoder堆叠而成,这里假设有6个:

对于每个encoder,包含self-attention与feed forward两个层:

对于每个decoder,包含mask self-attention, encoder decoder attention, feed forward三个层:

以上就是transformer模型的总体结构。
详述
self-attention
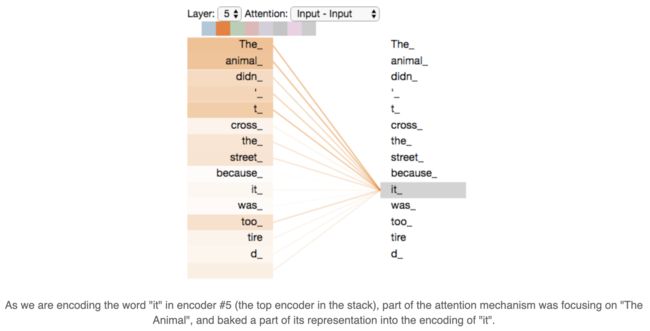
这个句子中的 it 是一个指代词,那么 it 指的是什么呢?它是指 animal 还是street?这个问题对人来说,是很简单的,但是对模型来说并不是那么容易。但是,如果模型引入了Self Attention机制之后,便能够让模型把it和animal关联起来了。同样的,当模型处理句子中其他词时,Self Attention机制也可以使得模型不仅仅关注当前位置的词,还会关注句子中其他位置的相关的词,进而可以更好地理解当前位置的词。
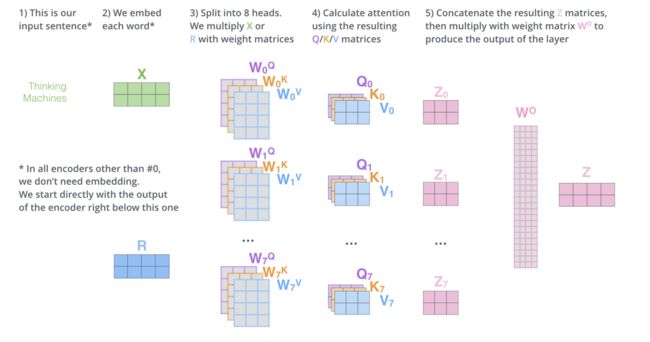
那么self-attention是怎样计算的呢?以"thinking machines"为例:
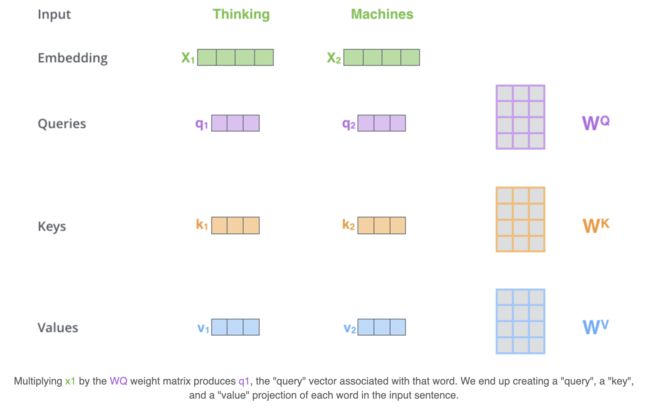 假设Thinking、Machines这两个单词经过词向量算法得到向量是 X 1 , X 2 X_1, X_2 X1,X2:
假设Thinking、Machines这两个单词经过词向量算法得到向量是 X 1 , X 2 X_1, X_2 X1,X2:
q 1 = X 1 W Q , q 2 = X 2 W Q ; k 1 = X 1 W K , k 2 = X 2 W K ; v 1 = X 1 W V , v 2 = X 2 W V , W Q , W K , W K ∈ R d x × d k q_1 = X_1 W^Q, q_2 = X_2 W^Q; \\k_1 = X_1 W^K, k_2 = X_2 W^K;\\v_1 = X_1 W^V, v_2 = X_2 W^V, \\W^Q, W^K, W^K \in \mathbb{R}^{d_x \times d_k}\ q1=X1WQ,q2=X2WQ;k1=X1WK,k2=X2WK;v1=X1WV,v2=X2WV,WQ,WK,WK∈Rdx×dk
接下来,计算score:
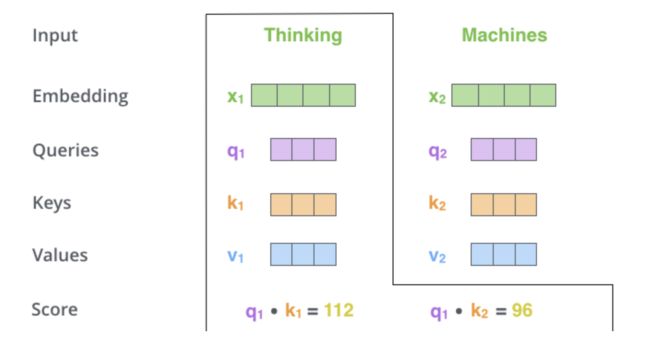

s c o r e 11 = q 1 ⋅ k 1 d k , s c o r e 12 = q 1 ⋅ k 2 d k ; s c o r e 21 = q 2 ⋅ k 1 d k , s c o r e 22 = q 2 ⋅ k 2 d k ; s c o r e 11 = e s c o r e 11 e s c o r e 11 + e s c o r e 12 , s c o r e 12 = e s c o r e 12 e s c o r e 11 + e s c o r e 12 ; s c o r e 21 = e s c o r e 21 e s c o r e 21 + e s c o r e 22 , s c o r e 22 = e s c o r e 22 e s c o r e 21 + e s c o r e 22 score_{11} = \frac{q_1 \cdot k_1}{\sqrt{d_k}} , score_{12} = \frac{q_1 \cdot k_2}{\sqrt{d_k}} ;\\ score_{21} = \frac{q_2 \cdot k_1}{\sqrt{d_k}}, score_{22} = \frac{q_2 \cdot k_2}{\sqrt{d_k}}; \\score_{11} = \frac{e^{score_{11}}}{e^{score_{11}} + e^{score_{12}}},score_{12} = \frac{e^{score_{12}}}{e^{score_{11}} + e^{score_{12}}}; \\score_{21} = \frac{e^{score_{21}}}{e^{score_{21}} + e^{score_{22}}},score_{22} = \frac{e^{score_{22}}}{e^{score_{21}} + e^{score_{22}}} score11=dkq1⋅k1,score12=dkq1⋅k2;score21=dkq2⋅k1,score22=dkq2⋅k2;score11=escore11+escore12escore11,score12=escore11+escore12escore12;score21=escore21+escore22escore21,score22=escore21+escore22escore22
计算 z z z:

z 1 = v 1 × s c o r e 11 + v 2 × s c o r e 12 ; z 2 = v 1 × s c o r e 21 + v 2 × s c o r e 22 z_1 = v_1 \times score_{11} + v_2 \times score_{12}; z_2 = v_1 \times score_{21} + v_2 \times score_{22} z1=v1×score11+v2×score12;z2=v1×score21+v2×score22
这就是self-attention的计算过程,其对应的代码如下:
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn
seaborn.set_context(context="talk")
%matplotlib inline
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1)
# query * key /sqrt d_k
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
if mask is not None:
# mask 单独处理
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
为什么要除以 d k \sqrt{d_k} dk
这里参考了Transformer和Bert相关知识解答的解答
more information : https://kexue.fm/archives/8620
论文中的解释是:向量的点积结果会很大,将softmax函数push到梯度很小的区域,scaled会缓解这种现象。方差太大会导致softmax的分母很大,从而将结果推入到梯度很小的区域,造成参数更新困难。但是为什么选择用 d k \sqrt{d_k} dk进行缩放呢? 目的是为了让方差变成1。
假设 q , k q,k q,k都是均值为0,方差为1的随机变量,那么 q ⋅ k q\cdot k q⋅k均值为0,方差为 d k d_k dk,因此 D ( q ⋅ k d k ) = d k d k 2 = 1 D(\frac{q\cdot k}{\sqrt{d_k}})=\frac{d_k}{\sqrt{d_k}^2}=1 D(dkq⋅k)=dk2dk=1。
多头注意力机制
Transformer 的论文通过增加多头注意力机制(一组注意力称为一个 attention head),进一步完善了Self-Attention。这种机制从如下两个方面增强了attention层的能力:
- 它扩展了模型关注不同位置的能力。在上面的例子中,第一个位置的输出 z 1 z_1 z1包含了句子中其他每个位置的很小一部分信息,但 z 1 z_1 z1仅仅是单个向量,所以可能仅由第1个位置的信息主导了。而当我们翻译句子:The animal didn’t cross the street because it was too tired时,我们不仅希望模型关注到"it"本身,还希望模型关注到"The"和“animal”,甚至关注到"tired"。这时,多头注意力机制会有帮助。
- 多头注意力机制赋予attention层多个“子表示空间”。下面我们会看到,多头注意力机制会有多组 W Q , W K , W V W^Q, W^K,W^V WQ,WK,WV 的权重矩阵(在 Transformer 的论文中,使用了 8 组注意力),因此可以将 X X X变换到更多种子空间进行表示。接下来我们也使用8组注意力头(attention heads)。每一组注意力的权重矩阵都是随机初始化的,但经过训练之后,每一组注意力的权重 W Q , W K , W V W^Q, W^K ,W^V WQ,WK,WV 可以把输入的向量映射到一个对应的"子表示空间"。
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
# d_model 能整除 h
assert d_model % h == 0
# d_v = d_k
self.d_k = d_model // h
self.h = h
# w_q,w_k,w_v
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) query->Q,key->K,value->V (将其拆开,split to 每个头去计算)
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) 计算attention
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) 将多头的结果拼接起来,比如:[64,12,6,50] -> [64,12,300]
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
feed forword
如前文所述,在self-attention层后跟着feed forword层,这就是一个简单的前馈网络,我们直接给出代码:
class PositionwiseFeedForward(nn.Module):
"Implements FFN equation."
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
残差连接
到目前为止,我们计算得到了self-attention的输出向量。而单层encoder里后续还有两个重要的操作:残差链接、标准化。编码器的每个子层(Self Attention 层和 FFN)都有一个残差连接和层标准化(layer-normalization),如下图所示。
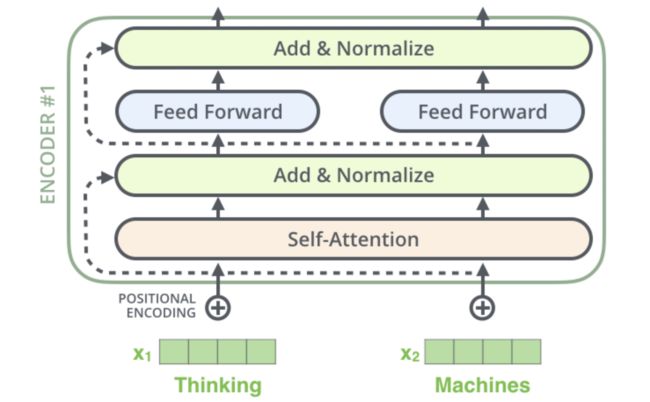
代码如下:
# sublayerconn 是做一个残差链接,然后连一个layernorm
class SublayerConnection(nn.Module):
def __init__(self,size,dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self,x,sublayer):
return x+self.dropout(sublayer(self.norm(x)))
经过前文,我们知道,编码器就是由self-attention和feed forward组合而成的,因此,我们可以写出编码器的代码。
编码器
# 每个encode是用self attn ,add norm and feed forward + add norm
class EncoderLayer(nn.Module):
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
# add & norm
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
class Encoder(nn.Module):
"完整的Encoder包含N层"
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"每一层的输入是x和mask"
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
解码器
解码器使用的self-attention为mask self-attention,即在解码器里,Self Attention 层只允许关注到输出序列中早于当前位置之前的单词。具体做法是:在 Self Attention 分数经过 Softmax 层之前,屏蔽当前位置之后的那些位置(将attention score设置成-inf)。
解码器 Attention层是使用前一层的输出来构造Query 矩阵,而Key矩阵和 Value矩阵来自于编码器最终的输出。
因此,代码如下:
# 每个decoder是用self attn, attn , fc构成的
class DecoderLayer(nn.Module):
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
# mask self-attention,这里的处理是将mask的部分设置为1e-9
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
# encoder decoder attention, key与value来自编码器
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
class Decoder(nn.Module):
"Generic N layer decoder with masking."
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
这样我们就可以将encoder 和 decoder组合起来:
# 将他们组合起来
class EncoderDecoder(nn.Module):
"""
基础的Encoder-Decoder结构。
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
"Take in and process masked src and target sequences."
return self.decode(self.encode(src, src_mask), src_mask,
tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
线性层和softmax
Decoder 最终的输出是一个向量,其中每个元素是浮点数。我们怎么把这个向量转换为单词呢?这是线性层和softmax完成的。
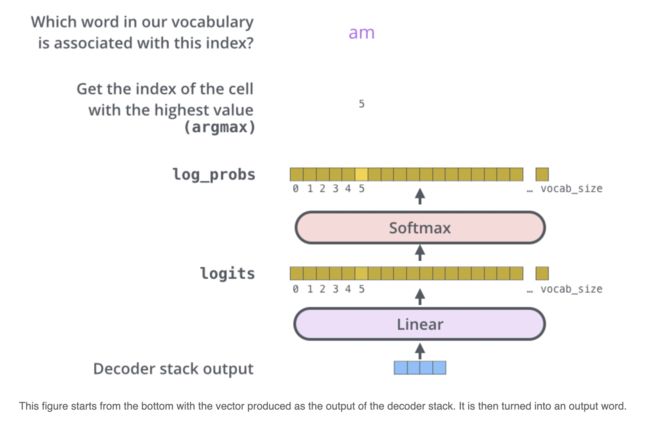
代码如下:
class Generator(nn.Module):
"定义生成器,由linear和softmax组成"
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)
通过上述的分析,我们就可以构造一个模型:
# 构造model
src_vocab = 10
tgt_vocab = 10
N = 2
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn),
c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
介绍完模型,文章的最后,介绍一下transformer的输入层。
输入层
他是由词向量与位置向量两部分构成的。self-attention虽然可以具有长程信息,但是他其实是天然对称的,也就是说 f ( . . . , x . . . , y , . . . . ) = f ( . . . , y , . . . . x ) f(...,x...,y,....)=f(...,y,....x) f(...,x...,y,....)=f(...,y,....x),但是在NLP任务中,位置其实是一个蛮重要的特征,因此,就加入了位置向量:
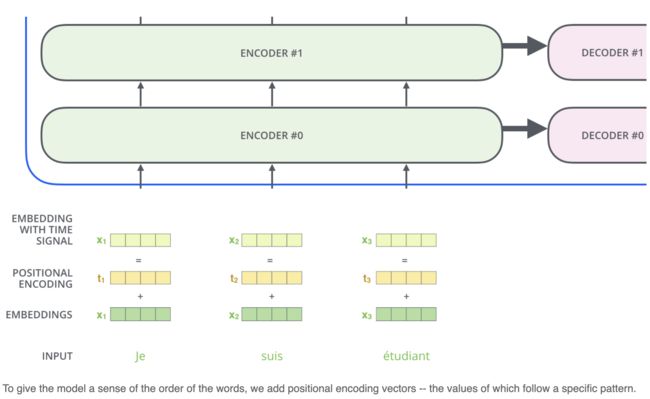
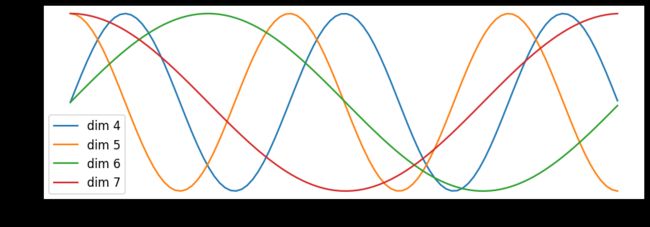
transformer这里用的是Sinusoidal位置编码:
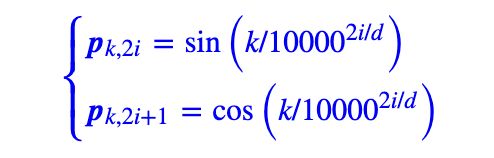
在探究其具体原因前,我们先看看怎么做:
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
class PositionalEncoding(nn.Module):
"Implement the PE function."
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
return self.dropout(x)
为什么要这么设计位置编码
本部分内容参考自:
Transformer升级之路:1、Sinusoidal位置编码追根溯源
因为attention模型本身是全对称的,即:
f ( ⋯ , x m , ⋯ , x n , ⋯ ) = f ( ⋯ , x n , ⋯ , x m , ⋯ ) f(\cdots,x_m,\cdots,x_n,\cdots)=f(\cdots,x_n,\cdots,x_m,\cdots) f(⋯,xm,⋯,xn,⋯)=f(⋯,xn,⋯,xm,⋯)
因此,我们要做的事情就是打破这种对称性,即在每个位置增加一个编码向量:
f ~ ( ⋯ , x m , ⋯ , x n , ⋯ ) = f ( ⋯ , x m + p m , ⋯ , x n + p n , ⋯ ) \widetilde f(\cdots,x_m,\cdots,x_n,\cdots)=f(\cdots,x_m+p_m,\cdots,x_n+p_n,\cdots) f (⋯,xm,⋯,xn,⋯)=f(⋯,xm+pm,⋯,xn+pn,⋯)
这样,只要每个位置的位置编码不同,其对称性就被打破了。但是transformer为什么使用Sinusoidal作为位置编码呢?它具有什么样的性质呢?
他需要具备以下性质:
- 能够表达两个位置的相对位置的信息;
- 具有远程衰减的作用。
如何表达相对位置的信息?
如果将 f ( ⋯ , x m + p m , ⋯ , x n + p n , ⋯ ) f(\cdots,x_m+p_m,\cdots,x_n+p_n,\cdots) f(⋯,xm+pm,⋯,xn+pn,⋯)中的位置编码看成是扰动项(为了简化问题,先只考虑m和n两个位置),对其进行泰勒二阶展开,我们有:

可以看出,第一项与位置无关,2-5项只依赖于单一位置;第6项包含两个位置的信息,将其记作 p m T H p n p_m^THp_n pmTHpn,希望这一项能表达相对位置的信息。
从简单的例子入手,假设 H H H是单位矩阵 I I I,那么 p m T H p n = p m T p n p_m^THp_n=p_m^Tp_n pmTHpn=pmTpn,我们希望它能够表达相对位置的信息,即:
g ( p m − p n ) = p m T p n = < p m , p n > (1) g(p_m-p_n)=p_m^Tp_n=
这里 p m p_m pm和 p n p_n pn是d维向量,假设是2维向量,借助复数来推导,即对向量 [ x , y ] = x + y i [x,y]=x+yi [x,y]=x+yi,根据复数的乘法法则,我们得到:
< p m , p n > = R e [ p m p n ∗ ]
其中, p n ∗ p_n^* pn∗是 p n p_n pn的共轭复数, R e [ ] Re[] Re[]表示复数的实部,为了能满足式(1),我们需要存在复数 q m − n q_{m-n} qm−n使得:
p m p n ∗ = q m − n p_mp_n^*=q_{m-n} pmpn∗=qm−n
两边取实部,就可以满足式(1)。为了求解这个方程,使用复数的指数形式:

- 对于第一个方程,带入 n = m ⇒ r n 2 = R 0 n=m⇒ r_n^2=R_0 n=m⇒rn2=R0,即 r n r_n rn是一个常数,这里就设为1;
- 对于第二个方程,带入 n = 0 ⇒ ϕ m − ϕ 0 = Φ m n=0⇒ \phi_m-\phi_0=\Phi_m n=0⇒ϕm−ϕ0=Φm,假设 ϕ 0 = 0 ⇒ ϕ m = Φ m ⇒ ϕ m − ϕ n = ϕ m − n \phi_0=0⇒ \phi_m=\Phi_m⇒ \phi_m-\phi_n=\phi_{m-n} ϕ0=0⇒ϕm=Φm⇒ϕm−ϕn=ϕm−n,令n=m-1,则有: ϕ m − ϕ n = ϕ 1 \phi_m-\phi_n=\phi_1 ϕm−ϕn=ϕ1,说明这是一个等差数列,通解是 m θ m\theta mθ。
经过上述分析,我们有 p m = e i m θ p_m=e^{im\theta} pm=eimθ,则有:

将这个2维的结果,推广到d维,由于内积满足线性叠加性,所以更高维的偶数维位置编码,我们可以表示为多个二维位置编码的组合:

同样满足式(1),这个解是式(1)的一个解。它跟标准的Sinusoidal位置编码形式基本一样了,只是sin,cos的位置有点不同。一般情况下,神经网络的神经元都是无序的,所以哪怕打乱各个维度,也是一种合理的位置编码,因此除了各个 θ i \theta_i θi没确定下来外,其实。
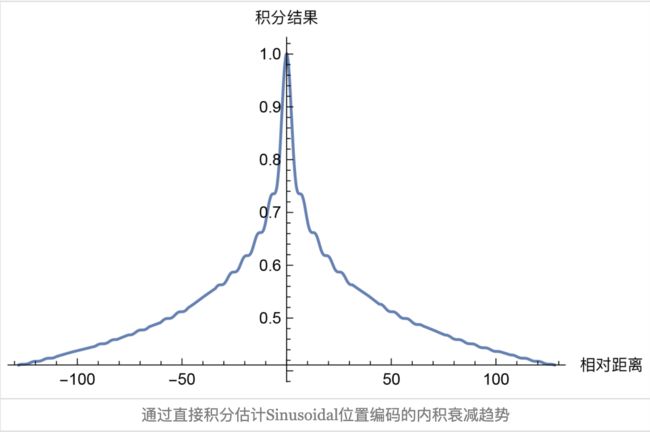
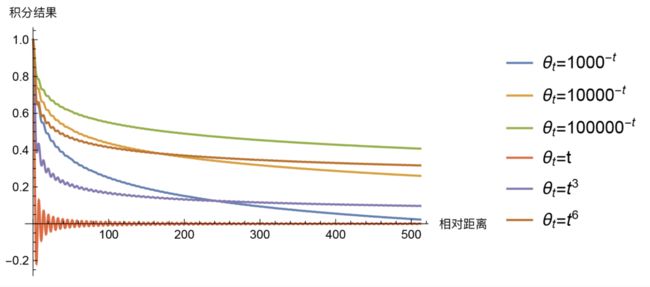
远程衰减:
transformer的选择是 θ i = 1000 0 − 2 i / d \theta_i=10000^{-2i/d} θi=10000−2i/d,为什么这么选择呢?因为这个形式有一个良好的性质:它使得随着 ∣ m − n ∣ |m−n| ∣m−n∣的增大, ⟨ p m , p n ⟩ ⟨p_m,p_n⟩ ⟨pm,pn⟩有着趋于零的趋势。