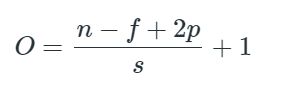PyTorch-模型建立
文章目录
- Fashion-MNIST数据集介绍
-
- 什么是MNIST?
- 什么是Fashion-MNIST?
-
- 是什么让MNIST成为Fashion MNIST?
- Fashion MNIST是怎么创建的?
- 通过PyTorch进行数据集加载
-
- 数据准备
- Datasets 和 DataLoaders
- 批量处理
- 模型建立
-
- python中的面向对象(OOP)
- PyTorch中的torch.nn
-
- nn.Module中的forward()方法
- PyTorch中的nn.functional包
- 定义神经网络的层作为类的属性
- 网络中的层layer
-
- Parameter Vs Argument
- 两种类型的Parameters
- Hyperparameters
- Data dependent hyperparameters
- Kernel和Filter
- 关于参数总结
- weight-神经网络的可学习参数
-
- 重写类方法
- 访问网络的层
- PyTorch中的Parameter类
- 可调用层(Callable Layers)
- 前向传播实现
-
- 输入层
- 卷积层:第一层和第二层
- 全连接层:第3层和第4层
- 输出层:第五层
- 总结
- 前向传播过程的解释
- 批量预测
- 单批次训练完整训练过程
- 训练集上循环完整代码
- 模型的评估-混淆矩阵的构建
Fashion-MNIST数据集介绍
数据是深度学习的主要组成部分,让我们的神经网络从数据中学习是我们的任务。
了解一个数据集需要知道的一些知识?
- 谁创建了数据集?
- 数据集是如何创建的?
- 使用了哪些转换?
- 数据集有什么目的?
- 可能的意外后果?
- 数据集有偏见吗?
- 数据集是否存在道德问题?
什么是MNIST?
MNIST数据集是美国国家标准与技术研究所(National Institute of Standards and Technology)修改后的数据库,是一个著名的手写数字数据集,通常用于培训机器学习的图像处理系统。NIST代表国家标准与技术研究所。
M 在MNIST代表modified,这是因为NIST有一个原始的数字数据集,它被修改为MNIST。

MNIST因数据集的使用频率而闻名。这很常见,有两个原因:
- 初学者使用它是因为它很简单
- 研究人员用它来衡量(比较)不同的模型。
- 该数据集由70000张手写数字图像组成,分割如下:6万张训练图片和10000张测试图像这些图片最初是由美国人口普查局员工和美国高中生创作的。
- MNIST已经得到了广泛的应用,图像识别技术也有了很大的改进,以至于人们认为数据集过于简单。这就是为什么要创建Fashion MNIST数据集。
什么是Fashion-MNIST?
Fashion MNIST顾名思义就是一个时装项目的数据集。具体而言,该数据集包含以下十类时尚项目:
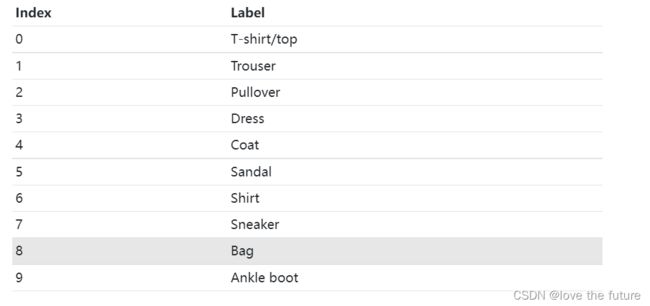
Fashion MNIST基于Zalando网站上的分类。Zalando是一家总部位于德国的跨国时尚商业公司,成立于2008年。这就是为什么我们可以在GitHub URL中看到 zalando research,在那里可以下载Fashion MNIST数据集。Zalando Research是创建该数据集的公司内部的团队。
是什么让MNIST成为Fashion MNIST?
fashion MNIST数据集以MNIST命名的原因是创作者试图用fashion MNIST替换MNIST。出于这个原因,时装数据集被设计成尽可能接近原始MNIST数据集,同时由于其数据比手写图像更复杂,导致训练难度更高。将在本文中看到Fashion MNIST镜像原始数据集的具体方式,但我们已经看到了类的数量。MNIST–有10个类(每个数字0-9对应一个)Fashion MNIST-有10个类(这是有意的)
论文地址:https://arxiv.org/pdf/1708.07747.pdf
数据集地址:https://github.com/zalandoresearch/fashion-mnist.
在这篇论文的摘要中可以看到:我们展示了Fashion MNIST,这是一个新的数据集,包含来自10个类别的70000件时装产品的28×28灰度图像,每个类别有7000张图像。训练集有60000张图像,测试集有10000张图像。Fashion MNIST旨在作为原始MNIST数据集的直接替代品,用于对机器学习算法进行测试,因为它共享相同的图像大小、数据格式以及训练和测试拆分结构。
另外,MNIST如此受欢迎的原因与它的规模有关,它允许深度学习研究人员快速检查并原型化他们的算法。此外,所有机器学习库(如scikit learn)和深度学习框架(如Tensorflow、PyTorch)都提供了辅助函数和方便的示例,可以使用MNIST开箱即用。
PyTorch确实为我们提供了一个名为torchvision的软件包,使我们能够轻松开始MNIST和Fashion MNIST。
Fashion MNIST是怎么创建的?
与MNIST数据集不同,时装集不是手工绘制的,但数据集中的图像是Zalando网站上的真实图像。然而,它们已被转换为更符合MNIST规范。这是网站上每张图片的一般转换过程:
- 转换为PNG
- 修剪
- 调整
- 大小
- 锐化
- 延长
- 否定
- 灰度
通过PyTorch进行数据集加载
提取、转换和加载即Extract, Transform, And Load (ETL)
建立一个项目的一般过程:
- 准备数据
- 建立模型
- 训练模型
- 分析模型的结果
数据准备
我们将从准备数据开始。为了准备数据,我们将遵循一个大致被称为ETL的过程。
- 从数据源中提取数据。
- 将数据转换为理想的格式。
- 将数据加载到合适的结构中。
ETL过程可以被认为是一个分形过程,因为它可以应用于各种规模。这个过程可以在小范围内应用,比如单个程序,也可以在大范围内应用,一直到企业级,在企业级有巨大的系统处理每个单独的部件。
首先需要导入所有必要的库: - torch:是顶级PyTorch软件包和tensor库。
- torch.nn :包含用于构建神经网络的模块和可扩展类的子包。
- torch.autograd :支持PyTorch中所有的可微张量运算的子包
- torch.nn.functional :一种功能接口,包含用于构建神经网络的典型操作,如损失函数、激活函数和卷积运算
- torch.optim :包含标准优化操作(如SGD和Adam)的子包。
- torch.utils :工具包,包含数据集和数据加载程序等实用程序类的子包,使数据预处理更容易
- torchvision :一个软件包,提供对流行数据集、模型架构和计算机视觉图像转换的访问。
- torchvision.transforms:转换包,含用于图像处理的常见转换的接口
pdb是Python调试器,带注释的导入是一个本地文件,用于绘制混淆矩阵,最后一行设置PyTorch print语句的打印选项。
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
#from plotcm import plot_confusion_matrix
数据准备:
Extract –从源文件中获取时尚Fashion MNIST图像数据。
Transform – 将数据转换为张量形式
Load – 将数据放入对象中,使其易于访问.
为此,PyTorch提供了两个类:
- torch.utils.data.Dataset:用于表示数据集的抽象类。
- torch.utils.data.DataLoader: 包装数据集并提供对底层数据的访问
抽象类是一个Python类,它有我们必须实现的方法,因此我们可以通过创建扩展dataset类功能的子类来创建自定义dataset。
为了使用PyTorch创建自定义数据集,我们通过创建实现这些必需方法的子类来扩展dataset类。这样做之后,我们的新子类就可以被传递给PyTorch数据加载程序对象。
我们将使用torchvision软件包内置的fashion MNIST数据集,因此我们的项目不必编写自定义的子类。只需知道Fashion MNIST内置的dataset类是在幕后完成这项工作的。
所有Dataset的子类必须重写提供数据集大小的__len__方法,getitem,支持从0到len(self)的整数索引。
具体来说,需要实现两种方法。 - 返回数据集长度的__len__方法,
- 以及从数据集中特定索引位置的数据集中获取元素的__getitem__方法。
torchvision包提供了下面的具体功能:
- Datasets (like MNIST and Fashion-MNIST)
- Models (like VGG16)
- Transforms(转换函数)
- Utils(工具包)
Fashion MNIST数据集只是扩展MNIST数据集并覆盖URL。
以下是PyTorch的torchvision源代码中的类定义:
class FashionMNIST(MNIST):
"""`Fashion-MNIST `_ Dataset.
Args:
root (string): Root directory of dataset where ``processed/training.pt``
and ``processed/test.pt`` exist.
train (bool, optional): If True, creates dataset from ``training.pt``,
otherwise from ``test.pt``.
download (bool, optional): If true, downloads the dataset from the internet and
puts it in root directory. If dataset is already downloaded, it is not
downloaded again.
transform (callable, optional): A function/transform that takes in an PIL image
and returns a transformed version. E.g, ``transforms.RandomCrop``
target_transform (callable, optional): A function/transform that takes in the
target and transforms it.
"""
urls = [
'http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-images-idx3-ubyte.gz',
'http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-labels-idx1-ubyte.gz',
'http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-images-idx3-ubyte.gz',
'http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-labels-idx1-ubyte.gz',
]
利用torchvision可以简化操作
加载数据集只需要执行以下的代码:
train_set = torchvision.datasets.FashionMNIST(
root='./data'
,train=True
,download=True
,transform=transforms.Compose([
transforms.ToTensor()
])
)
参数介绍:
- root 数据所在的磁盘位置
- train 数据集是否为训练集
- download 数据是否下载,第一次的时候,数据会从网上进行下载。
- transform 在数据元素上执行的转换组合。即讲数据元素转换成Tensor。
因为我们想把图像转换成张量,所以我们使用内置的转换。由于这个数据集将用于训练,我们将把实例命名为train_set。当我们第一次运行此代码时,Fashion MNIST数据集将在本地下载。后续通话会在下载数据之前检查数据。因此,我们不必担心重复下载或重复网络通话。
PyTorch DataLoader
创建DataLoader:
train_loader = torch.utils.data.DataLoader(train_set
,batch_size=1000
,shuffle=True
)
参数介绍:
- batch_size :一个批次的大小(1000 )
- shuffle :是否进行乱序(本例中选择的是)
- num_workers :进程数量(默认 0 表示只是用主线程)
Datasets 和 DataLoaders
从上文中我们已经得到了两个对象实例:train_set和train_loader
要查看训练集中有多少图像,我们可以使用Python中的len()函数检查数据集的长度
如果想查看每个图像的标签可以使用 train_set.targets。
如果想查看数据集中每个标签的数量,可以使用PyTorch中bincount()函数
len(train_set)
train_set.targets
train_set.targets.bincount() #表示每一类有6000张图像。
#tensor([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000])
类的平衡性:
通过上面的数据表明Fashion MNIST数据集在每个类中的样本数量上是一致的。这意味着每个类有6000个样品。因此,这个数据集被认为是平衡的。如果类具有不同数量的样本,我们会将该集合称为不平衡数据集。
类不平衡是一个常见的问题,但在Fashion MNIST数据集中,数据集是平衡的。
访问训练集中的数据:
为了从训练集中访问单个元素,我们首先将train_set对象传递给Python的iter()内置函数,该函数返回一个表示数据流的对象。
对于数据流,我们可以使用Python内置的next()函数来获取数据流中的下一个数据元素。我们希望从中得到一个样本,因此我们将相应地命名结果:
sample = next(iter(train_set))
len(sample)#2
将样本传递给len()函数后,我们可以看到样本包含两个项,这是因为数据集包含图像标签对。我们从训练集中检索的每个样本都包含作为张量的图像数据和作为张量的相应标签。(特征值,标签)的形式
由于样本是 sequence类型(tuple),我们可以使用sequence unpacking来分配图像和标签。现在,我们将检查图像和标签的类型,将其分解成PyTorch.Tensor类型
sample = next(iter(train_set))
len(sample)
type(sample)
image, label = sample
type(image)#torch.Tensor
type(label)#int
查看数据的大小:
image是shape为[1, 28, 28]的张量,
label是标量张量值。
print(image.shape)#torch.Size([1, 28, 28])
print(torch.tensor(label).shape)#torch.Size([])
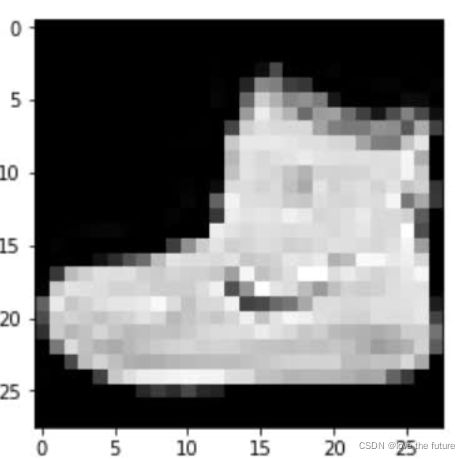
其中1表示的是颜色通道数为1 ,即为灰度图像。讲image压缩到28*28,然后绘制这张图像得到下面的结果,就是第一张图像的标签值为9,也就是第九类。
image.squeeze().shape #torch.Size([28, 28])
plt.imshow(image.squeeze(), cmap="gray")
torch.tensor(label)
#tensor(9)
批量处理
在上文中,得到图像的方式是通过使用 iter()、next()对train_set进行操作,我们也可以利用data_loader进行批量操作图像。
重新定义了一个加载器,batch=10值小一点,我们加载器中得到一批,就像我们在训练集中看到的那样。我们使用iter()和next()函数进行访问。在使用数据加载器时,有一件事需要注意。如果shuffle=True,则每次调用next时,批处理都会不同。当shuffle=True时,训练集中的第一个样本将在第一次调用next时返回。默认情况下,shuffle功能处于关闭状态。
由于batch_size=10,因此正在处理一批10幅图像和10个相应的标签。这就是为什么我们在变量名上使用复数。这些类型是我们期望的张量。然而,形状与我们在单个样本中看到的不同。我们没有使用单个标量值作为标签,而是使用了一个具有10个值的秩为1张量。包含图像数据的张量中每个维度的大小由以下每个值定义:(batch size, number of color channels, image height, image width)
display_loader = torch.utils.data.DataLoader(
train_set, batch_size=10
)
batch = next(iter(display_loader))
print('len:', len(batch)) #len: 2
images, labels = batch
print('types:', type(images), type(labels)) #types:
print('shapes:', images.shape, labels.shape) #shapes: torch.Size([10, 1, 28, 28]) torch.Size([10])
images[0].shape #torch.Size([1, 28, 28])
labels[0] #9
要绘制一批图像,我们可以使用torchvision.utils.make_grid()函数创建一个网格:
grid = torchvision.utils.make_grid(images, nrow=10)
plt.figure(figsize=(15,15))
plt.imshow(np.transpose(grid, (1,2,0)))
# plt.imshow(grid.permute(1,2,0))
print('labels:', labels)#labels: tensor([9, 0, 0, 3, 0, 2, 7, 2, 5, 5])

使用PyTorch中的DataLoader绘制图像
这是另外一种绘制图像的方法。
how_many_to_plot = 20
train_loader_iter = torch.utils.data.DataLoader(
train_set, batch_size=1, shuffle=True
)
plt.figure(figsize=(50,50))
for i, batch in enumerate(train_loader_iter, start=1):
image, label = batch
plt.subplot(10,10,i)
plt.imshow(image.reshape(28,28), cmap='gray')
plt.axis('off')
plt.title(train_set.classes[label.item()], fontsize=28)
if (i >= how_many_to_plot): break
plt.show()
模型建立
python中的面向对象(OOP)
准备好数据之后,就是建立模型,通常我们也说网络
为了在PyTorch中建立神经网络,我们扩展了Torch.nn.module的PyTorch类。这意味着我们需要在Python中使用一点面向对象编程(OOP)。更多关于Python的面向对象知识:https://docs.python.org/3/tutorial/classes.html
当我们编写程序或构建软件时,有两个关键组件,代码和数据。通过面向对象编程,我们将程序设计和结构定位于对象。对象是使用类在代码中定义的。类是定义对象的规范或规范,该规范指定类的每个对象应具有的数据和代码。
当我们创建一个类的对象时,我们称该对象为该类的实例,给定类的所有实例都有两个核心组件:
- Methods(方法)
- Attributes(属性)
方法代表代码,而属性代表数据,因此方法和属性由类定义。在一个给定的程序中,许多对象(即给定类的实例)可以同时存在,并且所有实例都将具有相同的可用属性和相同的可用方法。从这个角度来看,它们是一致的。同一类的对象之间的差异是对象中包含的每个属性的值。每个对象都有自己的属性值。这些值确定对象的内部状态。每个对象的代码和数据都封装在对象中。
class Lizard: #class declaration
def __init__(self, name): #class constructor (code)
self.name = name #attribute (data)
def set_name(self, name): #method declaration (code)
self.name = name #method implementation (code)
第一行声明类并指定类名,在本例中为testCNN。
第二行定义了一个称为类构造函数的特殊方法。在创建类的新实例时,会调用类构造函数。参数有self和name。
- self参数使我们能够创建存储或封装在对象中的属性值。当我们调用这个构造函数或任何其他方法时,我们不会传递self参数。Python会自动为我们做到这一点。
- 调用方可以任意传递任何其他参数的参数值(如name),这些传入方法的传递值可以在计算中使用,也可以在以后通过self进行保存和访问。
在完成构造函数之后,我们可以创建任意数量的方法,比如这里的方法set_name(),它允许调用者更改存储在self中的name值。我们在这里需要做的就是调用该方法并为名称传递一个新值。
test = testCNN('deep')
print(test.name)#deep
test.set_name('CNN')
print(test.name)#CNN
我们通过指定类名(testCNN)并传递构造函数参数(deep)来创建类的对象实例。构造函数将接收这些参数,并且构造函数代码将运行以保存传递的名称。
然后我们可以访问并打印名称,还可以调用set_name()方法来更改名称。一个程序中可以存在多个testCNN实例,每个实例都包含自己的数据。
从面向对象的角度来看,这个设置的重要部分是属性和方法被组织并包含在一个对象中。
现在让我们切换一下,看看面向对象编程如何与Py Torch相适应。
PyTorch中的torch.nn
在构建神经网络的时候,我们通常会利用PyTorch中的torch.nn软件包,里面包含了构建网络的基本组件,导入方法如下:
import torch.nn as nn
构建神经网络最主要的组件就是层,在PyTorch的神经网络库包含帮助我们构建层的类。nn.Module类
深层神经网络是使用多层结构构建的。这就是网络深度的原因。神经网络中的每一层都有两个主要组成部分:
- A transformation (code)
- A collection of weights (data)
与生活中的许多事情一样,这一事实使层成为使用OOP来表示对象的最佳候选对象。OOP是面向对象编程的缩写。
事实上,PyTorch就是这样。在nn包中,有一个名为Module的类,它是包含所有层的神经网络模块的基类。
这意味着PyTorch中的所有层都扩展了nn.Module类并继承nn.Module中的所有内置功能。在OOP中,这个概念被称为继承。
甚至神经网络也扩展了nn.Module类。神经网络和其中的层扩展了nn.Module类。这意味着我们如果需要在PyTorch中构建新层或神经网络,就必须extend nn.Module类。
nn.Module中的forward()方法
前向传播:当我们把一个张量作为输入传递给我们的网络时,张量通过每一层变换向前流动,直到张量到达输出层。张量通过网络向前流动的过程称为向前传递。
每一层都有自己的transformation(代码),张量向前通过每一层。每一层中的转换函数定义了整个网络的整体前向传播过程。
前向传播的目标是将输入转换或映射到正确的预测输出类,并且在训练过程中,各层权重(数据)的更新方式会导致映射进行调整,以使输出更接近正确的预测。
这意味着在PyTorch的nn.Module类中都有一个forward()方法,所以当我们构建层和网络时,我们必须提供forward()方法的实现。前向传播的过程实际就是这种数据变换的过程。
PyTorch中的nn.functional包
当我们实现nn.Module子类的forward()方法时,我们通常使用nn.functional中的函数,这个软件包为我们提供了许多可以用于构建层的神经网络操作。事实上,许多nn.Module类使用nn.functional中函数执行其操作的功能。
nn.functional包中包含nn.Module 类的方法用于实现其forward()函数。
建立神经网络的步骤:
- 1.继承(extend)nn.Module基类
- 2.将层定义为类的属性:在类构造函数中,使用torch.nn的预构建层将网络层定义为类属性
- 3.实现forward()方法。使用网络的层属性以及nn.functional中的操作来定义网络前向传递的函数API。
class Network:
def __init__(self):
self.layer = None
def forward(self, t):
t = self.layer(t)
return t
这为我们提供了一个简单的Network类,它在构造函数中有一个虚拟层,并为forward函数提供了一个虚拟实现。forward()函数的实现采用张量t,并使用虚拟层对其进行变换。转换张量后,返回新的张量。
但是该类尚未extend nn.Module类。让Network类extend到 nn.Module类中,我们还必须做两件事:
- 1.在第一行的Network后面加上括号class Network(nn.Module):
- 2.在构造函数的第3行插入对super类(父类)构造函数的调用。
class Network(nn.Module): # line 1
def __init__(self):
super().__init__() # line 3
self.layer = None
def forward(self, t):
t = self.layer(t)
return t
上面的 Network类由于extend了nn.Module类,因此具有nn.Module的所有功能。
定义神经网络的层作为类的属性
目前,我们的网络类有一个单独的虚拟层作为属性。现在让我们用PyTorch的nn库中为我们预先构建的一些真实层来替换它。我们正在构建一个CNN,所以我们将使用两种类型的层,即线性层和卷积层。
class Network(nn.Module):
def __init__(self):
super().__init__() #父类的构造函数
#两个卷积层
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
#两个全连接层
self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
#输出层
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
# implement the forward pass
return t
现在,我们有一个名为Network的Python类,它extend了PyTorch的nn.Module类。在我们的网络类中,我们有五个定义为属性的层。我们有两个卷积层self.conv1和self.conv2和三个线性层self.fc1,self.fc2,self.out.
我们在fc1和fc2中使用缩写fc,因为线性层也称为全连接层。它们还有第三个名字,我们有时可能会听到它叫“稠密”。所以线性、密集和全连接都是指同一类型的层。PyTorch使用单词linear,因此使用nn.linear类名来进行实现。out作为输出层。
网络中的层layer
在上文中,我们定义了2个卷积层和3个线性层,我们的每一层都扩展了PyTorch的神经网络Module类。对于每一层,有两个主要项目封装在里面,一个正向函数定义和一个权重张量。每个层中的权重张量包含在网络在训练过程中学习时更新的权重值,这就是我们将层指定为Network类中的属性的原因。
PyTorch的Module类跟踪每层中的权重张量。执行此跟踪的代码存在于nn.Module类中,由于我们extend了神经网络模块类,我们自动继承了这个功能。继承是我们上次讨论过的面向对象概念之一。我们所要做的就是利用这个功能,在我们的网络模块中将我们的层指定为属性,模块基类将看到这一点,并将权重注册为我们网络的可学习参数。
Parameter Vs Argument
parameter和argument这两个词有什么区别呢?
parameter在函数定义中用作占位符,而argument是传递给函数的实际值。parameter可以看作是函数内部的局部变量。
在我们的网络中,names是parameter,指定的值(value)是argument。
两种类型的Parameters
- 超参数(Hyperparameters)
- 数据相关超参数(Data dependent hyperparameters)
在神经网络中,Parameters是一个很松散的术语,无论是那种类型的Parameters,需要记住的就是Parameters是一个占位符,最终将保留或者具有一个值。
构造层时,我们将每个Parameters的值传递给层的构造函数。我们的卷积层有三个参数,线性层有两个参数。
Convolutional layers
in_channels
out_channels
kernel_size
Linear layers
in_features
out_features
Hyperparameters
一般来说,超参数是指其值是手动和任意选择的参数。作为神经网络程序员,我们选择超参数值主要基于尝试和错误,并越来越多地利用过去证明有效的值。为了构建CNN层,这些是我们手动选择的参数。这意味着我们只需选择这些参数的值。在神经网络编程中,这是很常见的,我们通常测试和调整这些参数,以找到最有效的值。
- kernel_size:设置过滤器的高度和宽度。
- out_channels:设置过滤器的深度(也就是过滤器的个数)。这是过滤器中的内核数。一个内核产生一个输出通道。
- out_features:设置输出张量的大小。
一种经常出现的模式是,我们在添加conv层时增加out_channels(6,12),在切换到线性层后,我们在过滤到输出类的数量时缩小out_features(120,60,10)。所有这些参数都会影响我们网络的架构。具体来说,这些参数直接影响层内的权重张量。
Data dependent hyperparameters
- in_channels
- in_features
- out_features
依赖于数据的超参数是其值依赖于数据的参数。突出的前两个数据相关超参数是第一卷积层的in_channels和输出层的out_features。
你看,第一个卷积层的in_channels(1)取决于组成训练集的图像中存在的颜色通道的数量。因为我们处理的是灰度图像,所以我们知道这个值应该是1。
输出层的out_features取决于我们的训练集中存在的类的数量。由于Fashion MNIST数据集中有10类服装,我们知道需要10个输出特性。
一般来说,一层的输入是前一层的输出,因此conv层中的所有in_channels和线性层中的in_features取决于来自前一层的数据。
当我们从conv层切换到线性层时,我们必须Flatten张量。这就是为什么我们有1244。12个来自前一层的输出通道数,但为什么我们有两个4?
Kernel和Filter
在深度学习中经常交替使用filter和kernel这两个词。然而,这两个概念在技术上有区别。
Kernel是2D张量(单个Kernel),Filter是包含内核集合的3D张量(包含多少个Kernel)。我们对单个通道应用内核,对多个通道应用过滤器。
关于参数总结
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
weight-神经网络的可学习参数
可学习参数是在训练过程中学习其值的参数。对于可学习的参数,我们通常从一组任意值开始,然后随着网络学习,这些值以迭代方式更新。事实上,当我们说一个网络正在学习时,我们的具体意思是网络正在学习可学习参数的适当值。适当的值是使损失函数最小化的值。
那这些可学习的参数在哪里?
这些可学习参数是网络的权重,存在于网络中的每一层。
在上文中定义的Network类,我们可以实例化:
network = Network()
实例化Network类的对象时,我们需要键入类名,后跟括号。当执行此代码时,会执行__init__构造函数中的代码,将我们的层指定为属性,然后返回。因此我们就可以通过Network类的实例变量访问该对象。
可以通过print函数打印出网络的结构。因为Network继承了nn.Module类,里面有方法实现了这个打印功能(类似tostring功能)。如果不继承nn.Module,打印出来的结果就不是这个
print(network)
# Network(
# (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
# (conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
# (fc1): Linear(in_features=192, out_features=120, bias=True)
# (fc2): Linear(in_features=120, out_features=60, bias=True)
# (out): Linear(in_features=60, out_features=10, bias=True)
# )
重写类方法
所有Python类都会自动继承Object类。如果我们想为我们的对象提供自定义字符串表示,我们可以这样做,但我们需要引入另一个面向对象的概念,称为覆盖(override)。当我们继承一个类时,我们得到了它的所有功能,为了补充这一点,我们可以添加额外的功能。然而,我们也可以通过改变现有功能来改变其行为,从而覆盖现有功能。重写__repr__方法即可。
def __repr__(self):
return "structure"
在OOP编程时,有构造函数__init__方法,以及它是如何构造对象的一种特殊Python方法。我们还会遇到其他一些特殊的方法,repr;就是其中之一。所有特殊的OOP Python方法通常都有双下划线的前置和后置.
访问网络的层
和很多的编程语言类似,python中也是通过点(.)来获得对象的属性方法。
下面时通过network对象访问网络中的每一层。
network.conv1
# Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
network.conv2
# Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
network.fc1
# Linear(in_features=192, out_features=120, bias=True)
network.fc2
# Linear(in_features=120, out_features=60, bias=True)
network.out
# Linear(in_features=60, out_features=10, bias=True)
得到每一层之后可以访问每一层中的权重
network.conv1.weight
# Parameter containing:
# tensor([[[[ 0.0692, 0.1029, -0.1793, 0.0495, 0.0619],
# [ 0.1860, 0.0503, -0.1270, -0.1240, -0.0872],
# [-0.1924, -0.0684, -0.0028, 0.1031, -0.1053],
# [-0.0607, 0.1332, 0.0191, 0.1069, -0.0977],
# [ 0.0095, -0.1570, 0.1730, 0.0674, -0.1589]]],
#
# [[[-0.1392, 0.1141, -0.0658, 0.1015, 0.0060],
# [-0.0519, 0.0341, 0.1161, 0.1492, -0.0370],
# [ 0.1077, 0.1146, 0.0707, 0.0927, 0.0192],
# [-0.0656, 0.0929, -0.1735, 0.1019, -0.0546],
# [ 0.0647, -0.0521, -0.0687, 0.1053, -0.0613]]],
#
# [[[-0.1066, -0.0885, 0.1483, -0.0563, 0.0517],
# [ 0.0266, 0.0752, -0.1901, -0.0931, -0.0657],
# [ 0.0502, -0.0652, 0.0523, -0.0789, -0.0471],
# [-0.0800, 0.1297, -0.0205, 0.0450, -0.1029],
# [-0.1542, 0.1634, -0.0448, 0.0998, -0.1385]]],
#
# [[[-0.0943, 0.0256, 0.1632, -0.0361, -0.0557],
# [ 0.1083, -0.1647, 0.0846, -0.0163, 0.0068],
# [-0.1241, 0.1761, 0.1914, 0.1492, 0.1270],
# [ 0.1583, 0.0905, 0.1406, 0.1439, 0.1804],
# [-0.1651, 0.1374, 0.0018, 0.0846, -0.1203]]],
#
# [[[ 0.1786, -0.0800, -0.0995, 0.1690, -0.0529],
# [ 0.0685, 0.1399, 0.0270, 0.1684, 0.1544],
# [ 0.1581, -0.0099, -0.0796, 0.0823, -0.1598],
# [ 0.1534, -0.1373, -0.0740, -0.0897, 0.1325],
# [ 0.1487, -0.0583, -0.0900, 0.1606, 0.0140]]],
#
# [[[ 0.0919, 0.0575, 0.0830, -0.1042, -0.1347],
# [-0.1615, 0.0451, 0.1563, -0.0577, -0.1096],
# [-0.0667, -0.1979, 0.0458, 0.1971, -0.1380],
# [-0.1279, 0.1753, -0.1063, 0.1230, -0.0475],
# [-0.0608, -0.0046, -0.0043, -0.1543, 0.1919]]]],
# requires_grad=True
# )
torch.Size([6, 1, 5, 5])
输出是一个张量,表示第一层卷积层的权值,当进行网络训练时,这些权重值会以这样一种方式更新,即损失函数最小化。
PyTorch中的Parameter类
为了跟踪网络中的所有权重张量。PyTorch有一个名为Parameter的特殊类。Parameter类继承了tensor类,因此每个层中的权重张量都是这个参数类的一个实例。这就是为什么我们在字符串表示输出的顶部看到Parameter containing:。
我们可以在Pytorch源代码中看到,Parameter类通过将Parameter containing:前置到常规张量类表示输出,来重写__repr__;函数。
def __repr__(self):
return 'Parameter containing:\n' + super(Parameter, self).__repr__()
PyTorch的nn.Module类基本上是寻找任何属性,这些属性的值是Parameter类的实例,当它找到Parameter类的实例时,它会跟踪它。
所有这些都是在幕后进行的技术细节。
这些权重的shape是怎么得到的呢?
卷积层的权重
对于卷积层,权重值存在于过滤器内部,在代码中,过滤器实际上是权重张量本身。层内的卷积运算是层内输入通道和滤波器之间的运算。这意味着我们真正拥有的是两个张量之间的运算。
对于第一个conv层,我们有一个颜色通道,应该由6个5x5大小的过滤器进行卷积,以产生6个输出通道。这就是我们如何解释层构造函数中的值。但在我们的层中,我们并没有明确地为6个过滤器中的每一个设置6个权重张量。实际上,我们用一个权重张量来表示所有6个过滤器。
第一个卷积层的权重张量的形状[6, 1, 5, 5]表明我们有一个秩4的权重张量。第一个轴的长度为6,这是6个过滤器的原因。表示有6个输出通道,1表示单个输入通道,后面的[5,5]表示的是卷积核大小。
第二个conv层有12个滤波器,因此有12个输出通道,而不是卷积单个输入通道,而是来自前一层的6个输入通道。
network.conv2.weight.shape
#torch.Size([12, 6, 5, 5])
(Number of filters, Depth, Height, Width)
- 所有过滤器都用一个张量表示。
- 过滤器的深度可以解释输入通道。
我们的张量是四阶张量。第一个轴表示过滤器的数量。第二个轴代表每个滤波器的深度,对应于被卷积的输入通道的数量。
最后两个轴代表每个过滤器的高度和宽度。我们可以通过索引权重张量的第一个轴来拉出任何一个过滤器。
全连接层的权重
对于全连接层,我们将秩为1的张量作为输入和输出。我们将全连接层中的in_features转换为out_features的方法是使用秩2张量,通常称为权重矩阵。这是因为权重张量的秩为2,具有高度和宽度轴。
network.fc1.weight.shape
#torch.Size([120,192]) = = > torch.Size([out_features,in_features])
全连接层的权重矩阵就是通常情况下的y=Ax+B的形式,A为权重矩阵,shape=[out_features,in_features]。
linear函数的源码如下:
# torch/nn/modules/linear.py (version 1.0.1)
def __init__(self, in_features, out_features, bias=True):
super(Linear, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.Tensor(out_features, in_features))
if bias:
self.bias = Parameter(torch.Tensor(out_features))
else:
self.register_parameter('bias', None)
self.reset_parameters()
下面是一段代码,通过输入in_features来调用linear层。我们可以这样调用对象实例,因为神经网络模块是可调用的Python对象。我们确实得到了一个包含三个元素的一维张量。然而,产生了不同的价值观。这是因为PyTorch创建了一个权重矩阵,并使用随机值对其进行初始化。这意味着两个例子中的线性函数是不同的,所以我们使用不同的函数来产生这些输出。
in_features = torch.tensor([1,2,3,4], dtype=torch.float32)
weight_matrix = torch.tensor([
[1,2,3,4],
[2,3,4,5],
[3,4,5,6]
], dtype=torch.float32)
weight_matrix.matmul(in_features)
#tensor([30., 40., 50.])
fc = nn.Linear(in_features=4, out_features=3, bias=False)
fc(in_features) #tensor([1.3524, 4.0868, 0.1020], grad_fn=)
可调用层(Callable Layers)
下面这种形式就是属于可调用层,可以进行调用的原因就是在PyTorch的模块类中实现了一种特殊的函数__call__(),如果某个类实现了__call__()方法,那么在调用对象实例的时候就会调用这个方法。
fc(in_features)
我们不直接调用forward()方法,而是调用对象实例。调用对象实例后,在引擎盖下调用__call__()方法,call()反过来调用forward()方法。这适用于所有神经网络模块,即网络和层。在PyTorch源代码中看到这一点。
# torch/nn/modules/module.py (version 1.0.1)
def __call__(self, *input, **kwargs):
for hook in self._forward_pre_hooks.values():
hook(self, input)
if torch._C._get_tracing_state():
result = self._slow_forward(*input, **kwargs)
else:
result = self.forward(*input, **kwargs)
for hook in self._forward_hooks.values():
hook_result = hook(self, input, result)
if hook_result is not None:
raise RuntimeError(
"forward hooks should never return any values, but '{}'"
"didn't return None".format(hook))
if len(self._backward_hooks) > 0:
var = result
while not isinstance(var, torch.Tensor):
if isinstance(var, dict):
var = next((v for v in var.values() if isinstance(v, torch.Tensor)))
else:
var = var[0]
grad_fn = var.grad_fn
if grad_fn is not None:
for hook in self._backward_hooks.values():
wrapper = functools.partial(hook, self)
functools.update_wrapper(wrapper, hook)
grad_fn.register_hook(wrapper)
return result
前向传播实现
模型构建的一般步骤如下:现在需要进行的就是建立模型阶段的第三个阶段
- 准备数据
- 建立模型
– 创建一个扩展神经网络的神经网络类。模块基类。
– 在类构造函数中,将网络的层定义为类属性。
– 还可以使用网络的层属性。用于定义网络前向传递的函数API操作。 - 训练模型
- 分析模型的结果
class Network(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12 * 4 * 4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
# implement the forward pass
return t
输入层
任何神经网络的输入层都由输入数据决定。例如,如果我们的输入张量包含三个元素,那么我们的网络将在其输入层中包含三个节点。
因此,我们可以将输入层视为身份转换。从数学上来说,这就是函数f(x)=x.
可以通过下面的方式显示标识,但是其实是没有必要的。
# (0) input layer
t = t
卷积层:第一层和第二层
这两个隐藏的卷积层在执行转换方面非常相似。在深度学习中,所有不是输入或输出层的层都被称为隐藏层,这就是为什么我们将这些卷积层称为隐藏层。
为了进行卷积运算,我们将张量传递给第一个卷积层的forward函数,self.conv1。我们已经了解了所有的PyTorch神经网络模块如何具有forward()方法,以及何时调用nn.Mudule中forward()方法,我们有一种特殊的调用方式。
当你想调用nn.Mudule中forward()方法时,我们调用实际实例,而不是直接调用forward()方法。
不是self.conv1.forward(tensor),而是self.conv1(tensor)。这就是前文中所讲到的可调用层。让我们继续添加实现这两个卷积层所需的所有调用。
# (1) hidden conv layer
t = self.conv1(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (2) hidden conv layer
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
当我们在卷积层中移动时,我们的输入张量t被转换。第一个卷积层有一个卷积操作,然后是一个relu激活操作,其输出随后被传递给一个最大池操作, kernel_size_size=2,stride=2。
然后,第一个卷积层的输出张量t被传递到下一个卷积层,结构与第一个卷积层相同。
这些层中的每一层都由一组权重(数据)和一组收集操作(代码)组成。权重封装在nn.Conv2d()类的实例中。relu()和max_pool2d()调用只是纯粹的操作。它们都没有权重,这就是为什么我们直接从nn.functional中调用API。
有时我们可能会看到称为池化层的池操作。有时我们甚至会听到被称为激活层的激活操作。然而,层与操作的区别在于层具有权重。由于池操作和激活函数没有权重,我们将它们称为操作,并将它们视为添加到层操作集合中。
例如,我们将说网络中的第一层是一个卷积层,它包含一组权重,并执行三个操作,一个卷积操作、relu激活操作和最大池操作。
请注意,这里的规则和术语并不严格。这只是描述网络的一种方式。还有其他方式来表达这些想法。我们需要注意的主要问题是,哪些操作是使用权重定义的,哪些操作不使用任何权重。一般来说,使用权重定义的操作就是我们所说的层。后来,其他操作被添加到混合中,比如激活函数和池操作,这在术语上造成了一些混乱。从数学上讲,整个网络只是函数的组合,而函数的组合就是函数本身。所以网络只是一个函数。所有的术语,如层、激活函数和权重,都只是用来帮助描述不同的部分。
全连接层:第3层和第4层
在我们将输入传递到第一个隐藏的线性层之前,我们必须reshape()或flatten张量。当我们把卷积层的输出作为输入传递给线性层时,情况就是这样。由于第3层是第一个线性层,我们将把reshape操作作为第3层的一部分。
# (3) hidden linear layer
t = t.reshape(-1, 12 * 4 * 4)
t = self.fc1(t)
t = F.relu(t)
# (4) hidden linear layer
t = self.fc2(t)
t = F.relu(t)
我们在前文中可以知道,reshape操作中的数字12由来自前一个卷积层的输出通道数决定。然而,44是一个没有解释的问题。现在让我们来揭示答案。44实际上是12个输出通道中每个通道的高度和宽度。
我们从一个1×28×28的输入张量开始。这给出了一个单色通道,28 x 28的图像,当我们的张量到达第一个线性层时,尺寸已经改变了。通过卷积和池运算,高度和宽度尺寸已从28 x 28减小到4 x 4。卷积和合并操作是高度和宽度维度上的缩减操作。其中原理就是卷积操作之后特征矩阵的一个变化公式。在张量被reshape之后,我们将张量传递给线性层,并将结果传递给relu()激活函数。
输出层:第五层
网络的第五层也是最后一层是线性层,我们称之为输出层。当我们把张量传递到输出层时,结果就是预测张量。由于我们的数据有十个预测类,我们知道我们的输出张量将有十个元素。
# (6) output layer
t = self.out(t)
#t = F.softmax(t, dim=1)
十个输出将对应于我们每个预测类的预测值。在网络内部,我们通常使用relu()作为我们的非线性激活函数,但对于输出层,每当我们试图预测一个类别时,我们就使用softmax()。softmax函数为每个预测类返回正概率,概率总和为1。
然而,在我们的例子中,我们不会使用softmax(),因为我们将使用的损失函数F.cross_entropy()会隐式地对其输入执行softmax()操作,所以我们只返回上一次线性变换的结果。
总结
最后,将上面的各层放在forward()函数中。
def forward(self, t):
# (1) input layer
t = t
# (2) hidden conv layer
t = self.conv1(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (3) hidden conv layer
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (4) hidden linear layer
t = t.reshape(-1, 12 * 4 * 4)
t = self.fc1(t)
t = F.relu(t)
# (5) hidden linear layer
t = self.fc2(t)
t = F.relu(t)
# (6) output layer
t = self.out(t)
#t = F.softmax(t, dim=1)
return t
前向传播过程的解释
为了更好的理解前向传播的整个过程,理解深度神经网络的实现,在进入训练之前,需要对前向传播中的部分细节进行解释。
什么是前向传播?
正向传播是将输入张量转换为输出张量的过程。神经网络的核心是将输入张量映射到输出张量的函数,而前向传播只是将输入传递到网络并从网络接收输出的过程的一个特殊名称。
正如我们所见,神经网络以张量的形式对数据进行操作。前向传播的概念用于表示输入张量数据通过网络向前传输。这就是为什么forward()方法名为forward,forward()的执行是向前传播的过程。如果您正在关注这个系列,我们现在知道,我们不直接调用forward()方法,而是调用网络实例(前文中讲到的可调用层)。还有一种反向传播(backpropagation)的概念,在训练过程中,反向传播发生在正向传播之后。
在我们的例子中,从实际的角度来看,前向传播是将输入图像张量传递给我们在上一集中实现的forward()方法的过程。这个输出是网络的预测。在关于数据集和数据加载器的一集中,我们看到了如何从我们的训练集中访问单个样本图像张量,更重要的是,如何从数据加载器访问一批图像张量。现在我们已经定义了网络并实现了forward()方法,将图像传递到网络以获得预测。
下面的代码可以控制是否启动梯度更新的功能,false表示不启动,true表示启动,在正式训练的时候,是需要开启的,因为训练过程需要进行梯度的更新。
torch.set_grad_enabled(False)
下面让我们构建一个简单的预测过程,将一张图片传入神经网络进行预测。
sample = next(iter(train_set))
image, label = sample
image.shape
#torch.Size([1, 28, 28])
由train_set得到的单个图像是[1, 28, 28],但是神经网络的输入需要(batch_size, in_channels, height, width)形式的输入,所以要对单张输入图像进行unsqueeze(),得到[1, 1, 28, 28],将其输入神经网络中进行预测。
# Inserts an additional dimension that represents a batch of size 1
image.unsqueeze(0).shape
#torch.Size([1, 1, 28, 28])
完整的预测代码如下:
network = Network()
sample = next(iter(train_set))
image, label = sample
pred = network(image.unsqueeze(0))
# image shape needs to be (batch_size × in_channels × H × W)
pred
#tensor([[0.0991, 0.0916, 0.0907, 0.0949, 0.1013, 0.0922, 0.0990, 0.1130, 0.1107, 0.1074]])表示每个类别的预测值
label
#9 表示该图片的真实标签值
pred.argmax(dim=1) #查看预测类别中概率最大的下标即为预测的类别,为7
从上面的过程可以看出,最后的预测tensor是([1, 10]),表示有一张图片和10个预测类别,即(batch size, number of prediction classes),对于批次中的每个输入,以及每个预测类,我们都有一个预测值。如果我们想让这些值成为概率,我们可以只使用nn.functional中的softmax()函数即可
F.softmax(pred, dim=1)
#tensor([[0.1096, 0.1018, 0.0867, 0.0936, 0.1102, 0.0929, 0.1083, 0.0998, 0.0943, 0.1030]])
F.softmax(pred, dim=1).sum()
#tensor(1.) 概率值的总和为1
上面的预测结果是错误的,因为网络中的权重是随机生成的,并且没有进行迭代的更新梯度,所以预测结果不准确。
- 关于这些结果,我们需要指出几件重要的事情。大多数概率接近10%,这是有意义的,因为我们的网络在猜测,我们有10个来自平衡数据集的预测类。
- 随机生成的权重的另一个含义是,每次我们创建网络的新实例时,网络中的权重都会不同。这意味着,如果我们创建不同的网络,我们得到的预测将不同。记住这一点。你的预测将与我们在这里看到的不同。
net1 = Network()
net2 = Network()
net1(image.unsqueeze(0))
#tensor([[ 0.0855, 0.1123, -0.0290, -0.1411, -0.1293, -0.0688, 0.0149, 0.1410, -0.0936, -0.1157]])
net2(image.unsqueeze(0))
#tensor([[-0.0408, -0.0696, -0.1022, -0.0316, -0.0986, -0.0123, 0.0463, 0.0248, 0.0157, -0.1251]])
前向传播过程矩阵shape的变换:
批量预测
在上面的讲述中,我们实现了单个图像的预测,在本小节中,我们将一个批次传递到网络中进行预测。
准备工作和上面的一样。
- Our imports.
- Our training set.
- Our Network class definition.
- To disable gradient tracking. (optional)
- A Network class instance.
现在我们将batch_size=10.
最后我们将返回的图像shape是(batch size, input channels, height, width)
data_loader = torch.utils.data.DataLoader(
train_set, batch_size=10
)
batch = next(iter(data_loader))
images, labels = batch
images.shape
#torch.Size([10, 1, 28, 28])
labels.shape
#torch.Size([10])
preds = network(images)
preds.shape
#torch.Size([10, 10]) #输出的shape(batch size, number of prediction classes)
preds
tensor(
[
[ 0.1072, -0.1255, -0.0782, -0.1073, 0.1048, 0.1142, -0.0804, -0.0087, 0.0082, 0.0180],
[ 0.1070, -0.1233, -0.0798, -0.1060, 0.1065, 0.1163, -0.0689, -0.0142, 0.0085, 0.0134],
[ 0.0985, -0.1287, -0.0979, -0.1001, 0.1092, 0.1129, -0.0605, -0.0248, 0.0290, 0.0066],
[ 0.0989, -0.1295, -0.0944, -0.1054, 0.1071, 0.1146, -0.0596, -0.0249, 0.0273, 0.0059],
[ 0.1004, -0.1273, -0.0843, -0.1127, 0.1072, 0.1183, -0.0670, -0.0162, 0.0129, 0.0101],
[ 0.1036, -0.1245, -0.0842, -0.1047, 0.1097, 0.1176, -0.0682, -0.0126, 0.0128, 0.0147],
[ 0.1093, -0.1292, -0.0961, -0.1006, 0.1106, 0.1096, -0.0633, -0.0163, 0.0215, 0.0046],
[ 0.1026, -0.1204, -0.0799, -0.1060, 0.1077, 0.1207, -0.0741, -0.0124, 0.0098, 0.0202],
[ 0.0991, -0.1275, -0.0911, -0.0980, 0.1109, 0.1134, -0.0625, -0.0391, 0.0318, 0.0104],
[ 0.1007, -0.1212, -0.0918, -0.0962, 0.1168, 0.1105, -0.0719, -0.0265, 0.0207, 0.0157]
]
)
预测结果的形状是10乘10,这给了我们两个轴,每个轴的长度是10。这反映了这样一个事实:我们有十幅图像,对于这十幅图像中的每一幅,我们有十个预测类。
第一维度的元素是长度为10的数组。这些数组元素中的每一个都包含对应图像的每个类别的十个预测。
第二维度的元素是数字。每个数字都是特定输出类的赋值。输出类由索引编码,因此每个索引代表一个特定的输出类。最大的那个索引就是预测的类别。
我们使用argmax()函数找出哪个索引包含最高的预测值。一旦我们知道哪个索引具有最高的预测值,我们就可以将索引与标签进行比较,看看是否存在匹配。为此,我们对预测张量调用argmax()函数,并指定第二维度。
preds.argmax(dim=1)
#tensor([5, 5, 5, 5, 5, 5, 4, 5, 5, 4])
labels
#tensor([9, 0, 0, 3, 0, 2, 7, 2, 5, 5])
#查看预测结果是否匹配
preds.argmax(dim=1).eq(labels)
# tensor(
# [False, False, False, False, False, False, False, False, True, False]
# )
#预测正确的个数
preds.argmax(dim=1).eq(labels).sum()
#tensor(1)
我们可以将最后一个调用封装到一个名为get_num_correct()的函数中,该函数接受预测和标签,并使用item()方法返回正确预测的Python数量。
def get_num_correct(preds, labels):
return preds.argmax(dim=1).eq(labels).sum().item()
get_num_correct(preds, labels)
#1
单批次训练完整训练过程
在完整的训练过程中需要计算损失值,梯度,更新权值。
上面针对单批次进行了实现,现在需要对每个批次重复这个过程,直到我们涵盖了培训集中的每个样本。在我们完成了所有批次的这个过程,并通过了训练集中的每个样本之后,我们说一个epoch已经完成。我们用epoch这个词来表示一个时间段,在这个时间段内,我们的整个训练集都被覆盖了。
在整个训练过程中,我们需要以下的一些步骤:
- 从培训集中获取batch。
- 将batch传递到网络。
- 计算损失(预测值和真实值之间的差值)。
- 计算损失函数的梯度和网络的权重。
- 使用梯度更新权重以减少损失。
- 重复步骤1-5,直到完成一个历元。
- 重复步骤1-6以达到最小损失所需的次数。
在正式的训练过程中,我们要开启梯度跟踪功能,(默认情况下是打开的)。
torch.set_grad_enabled(True)
训练过程
cross_entropy()函数返回一个标量值,因此我们使用item()方法将损失打印为Python数字。我们100个预测中有9个是正确的,因为我们有10个预测类,这是我们随机猜测的结果。
network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=100) #batch=100
batch = next(iter(train_loader)) # Getting a batch
images, labels = batch
preds = network(images)#预测
loss = F.cross_entropy(preds, labels) #计算损失
loss.item()#取出具体的值2.307542085647583
get_num_correct(preds, labels) #获得预测准确的个数 9
梯度计算:
使用PyTorch计算梯度非常容易。因为我们的网络是nn.Module,PyTorch创建了一个计算图。当我们的张量在网络中向前流动时,所有的计算都被添加到了图表中。然后,PyTorch使用计算图计算损失函数相对于网络权重的梯度。在计算梯度之前,让我们先确认conv1层中当前没有梯度。梯度是可以在每个层的权重张量的grad(梯度的缩写)属性中访问的张量。
network.conv1.weight.grad#None
为了计算梯度,我们对loss张量调用backward()方法,如下所示:
loss.backward() # Calculating the gradients
network.conv1.weight.grad.shape
# 可以得到每一层的梯度值:torch.Size([6, 1, 5, 5])
更新梯度
优化器使用这些梯度来更新相应的权重。为了创建优化器,我们使用torch.optim包中有许多优化算法的实现,我们可以使用。我们将以Adam为例。
我们将网络参数传递给Adam类构造函数(优化器就是这样访问梯度的),然后传递学习率。最后,我们要做的就是更新权重,告诉优化器使用梯度,朝着损失函数的最小值前进。
optimizer = optim.Adam(network.parameters(), lr=0.01)
optimizer.step() # Updating the weights
调用step()函数时,优化器使用存储在网络参数中的梯度更新权重。这意味着,如果我们再次通过网络传递同一批,我们的损失应该会减少。检查一下,我们可以看到事实确实如此
preds = network(images)
loss = F.cross_entropy(preds, labels)
loss.item()#2.262690782546997
get_num_correct(preds, labels)#15
所以,单个批次训练两次的代码如下:
network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
optimizer = optim.Adam(network.parameters(), lr=0.01)
batch = next(iter(train_loader)) # Get Batch
images, labels = batch
preds = network(images) # Pass Batch
loss = F.cross_entropy(preds, labels) # Calculate Loss
loss.backward() # Calculate Gradients
optimizer.step() # Update Weights
print('loss1:', loss.item())
preds = network(images)
loss = F.cross_entropy(preds, labels)
print('loss2:', loss.item())
#loss1: 2.3034827709198
#loss2: 2.2825052738189697
训练集上循环完整代码
现在,为了使用train_loader中的所有批处理进行培训,我们需要做一些更改,并添加一行额外的代码:增加一个循环,以及记录loss和正确率的变量:下面是所有训练集上的一次完整训练(an epoch)
network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
optimizer = optim.Adam(network.parameters(), lr=0.01)
total_loss = 0
total_correct = 0
for batch in train_loader: # Get Batch
images, labels = batch
preds = network(images) # Pass Batch
loss = F.cross_entropy(preds, labels) # Calculate Loss
optimizer.zero_grad()
loss.backward() # Calculate Gradients
optimizer.step() # Update Weights
total_loss += loss.item()
total_correct += get_num_correct(preds, labels)
print(
"epoch:", 0,
"total_correct:", total_correct,
"loss:", total_loss
)
#epoch: 0 total_correct: 42104 loss: 476.6809593439102
total_correct / len(train_set)
#0.7017333333333333
我们将创建一个for循环,迭代所有批次,而不是从数据加载器中获取单个批次。由于我们的训练集中有60000个样本,我们将有60000/100=600次迭代。出于这个原因,我们将从循环中删除print语句,并跟踪总损失以及最终打印它们的正确预测总数。
训练多个epoch:
network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
optimizer = optim.Adam(network.parameters(), lr=0.01)
for epoch in range(10):
total_loss = 0
total_correct = 0
for batch in train_loader: # Get Batch
images, labels = batch
preds = network(images) # Pass Batch
loss = F.cross_entropy(preds, labels) # Calculate Loss
optimizer.zero_grad() #每各batch之后都要讲梯度清零
loss.backward() # Calculate Gradients
optimizer.step() # Update Weights
total_loss += loss.item()
total_correct += get_num_correct(preds, labels)
print(
"epoch", epoch,
"total_correct:", total_correct,
"loss:", total_loss
)
最后训练之后的结果:我们可以看到正确值的数量增加,损失减少。
epoch 0 total_correct: 43301 loss: 447.59147948026657
epoch 1 total_correct: 49565 loss: 284.43429669737816
epoch 2 total_correct: 51063 loss: 244.08825492858887
epoch 3 total_correct: 51955 loss: 220.5841210782528
epoch 4 total_correct: 52551 loss: 204.73878084123135
epoch 5 total_correct: 52914 loss: 193.1240530461073
epoch 6 total_correct: 53195 loss: 184.50964668393135
epoch 7 total_correct: 53445 loss: 177.78808392584324
epoch 8 total_correct: 53629 loss: 171.81662507355213
epoch 9 total_correct: 53819 loss: 166.2412590533495
模型的评估-混淆矩阵的构建
混淆矩阵将向我们显示模型混淆的地方。更具体地说,混淆矩阵将向我们显示模型正确预测的类别以及模型错误预测的类别。对于错误的预测,我们将能够看到模型预测的类别,这将告诉我们哪些类别进行了错误的预测。
构建函数以获得所有样本的预测
我们将创建一个名为get_all_preds()的函数,并传递一个model和一个loader。model将用于获得预测,loader将用于提供训练集中的批次。该函数需要做的只是在loader上迭代,将批传递给模型,并将每个批的结果连接到一个预测张量,该预测张量将返回给调用者。
利用torch.cat将每一个批次的结果连接成一个张量。
@torch.no_grad()
def get_all_preds(model, loader):
all_preds = torch.tensor([])
for batch in loader:
images, labels = batch
preds = model(images)
all_preds = torch.cat(
(all_preds, preds)
,dim=0
)
return all_preds
这个函数内部会产生一个空的张量,所有这些张量都用来保存输出预测。然后,它迭代来自loader的batch,并将输出预测与all_preds张量连接起来。最后,所有的预测都返回给调用者。
注意,在顶部,我们使用@torch.no_grad()对函数进行了注释。这是因为我们希望这个函数的执行忽略梯度跟踪。这是因为梯度跟踪使用内存,在推理过程中(在不训练的情况下获得预测),不需要跟踪计算图。这个注解是在执行特定功能时局部关闭渐变跟踪功能的一种方式。
我们现在准备好调用获取训练集的预测。我们需要做的就是创建一个具有合理批量大小的数据加载器,并将模型和数据加载器传递给get_All_preds()函数。with torch.no_grad()表示关闭梯度跟踪。
with torch.no_grad():
prediction_loader = torch.utils.data.DataLoader(train_set, batch_size=10000)
train_preds = get_all_preds(network, prediction_loader)
现在,我们有了预测张量,我们可以将它传递给我们在上一集中创建的get_num_correct()函数,以及训练集标签,以获得正确预测的总数。
preds_correct = get_num_correct(train_preds, train_set.targets)
print('total correct:', preds_correct)
print('accuracy:', preds_correct / len(train_set))
#total correct: 53578
#accuracy: 0.8929666666666667
构造混淆矩阵
我们构建混淆矩阵的任务是根据真实值(目标)计算预测值的数量。这将创建一个矩阵,作为热图,告诉我们预测值相对于真实值的下降位置。
train_set.targets#真实值
#tensor([9, 0, 0, ..., 3, 0, 5])
train_preds.argmax(dim=1) #预测值
#tensor([9, 0, 0, ..., 3, 0, 5])
现在,如果我们在元素方面比较这两个张量,我们可以看到预测的标签是否与目标匹配。此外,如果我们计算预测标签与目标标签的数量,两个张量内的值将作为矩阵的坐标。让我们把这两个张量沿二维叠加,这样我们就可以有60000个有序对。
stacked = torch.stack(
(
train_set.targets
,train_preds.argmax(dim=1)
)
,dim=1
)
stacked.shape
#torch.Size([60000, 2]) #2表示的一列是真实值,一列是预测值
stacked
# tensor([
# [9, 9],
# [0, 0],
# [0, 0],
# ...,
# [3, 3],
# [0, 0],
# [5, 5]
# ])
stacked[0].tolist()
#[9, 9]
现在,我们可以迭代这些对,计算矩阵中每个位置的出现次数。让我们创建矩阵。因为我们有十个预测类别,我们将有一个十乘十的矩阵。
cmt = torch.zeros(10,10, dtype=torch.int64)
cmt
# tensor([
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
# ])
for p in stacked:
tl, pl = p.tolist()
cmt[tl, pl] = cmt[tl, pl] + 1
cmt
# tensor([
# [5637, 3, 96, 75, 20, 10, 86, 0, 73, 0],
# [ 40, 5843, 3, 75, 16, 8, 5, 0, 10, 0],
# [ 87, 4, 4500, 70, 1069, 8, 156, 0, 106, 0],
# [ 339, 61, 19, 5269, 203, 10, 72, 2, 25, 0],
# [ 23, 9, 263, 209, 5217, 2, 238, 0, 39, 0],
# [ 0, 0, 0, 1, 0, 5604, 0, 333, 13, 49],
# [1827, 7, 716, 104, 792, 3, 2370, 0, 181, 0],
# [ 0, 0, 0, 0, 0, 22, 0, 5867, 4, 107],
# [ 32, 1, 13, 15, 19, 5, 17, 11, 5887, 0],
# [ 0, 0, 0, 0, 0, 28, 0, 234, 6, 5732]
# ])
混淆矩阵的绘制
将实际的混淆矩阵生成为numpy.ndarray,我们使用sklearn.metrics中的confusion_matrix()函数
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from resources.plotcm import plot_confusion_matrix
对于from resources.plotcm import plot_confusion_matrix导入,请注意plotcm是一个名为plotcm.py的文件位于当前目录中名为resources的文件夹中。在plotcm.py文件中,我们将调用一个名为plot_confusion_matrix()的函数。
我们可以这样生成混淆矩阵:
cm = confusion_matrix(train_set.targets, train_preds.argmax(dim=1))
print(type(cm))
cm
#和上面的混淆矩阵不同,由于在不同的时间运行的
# plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, train_set.classes)
# Confusion matrix, without normalization
# [[5431 14 88 145 26 7 241 0 48 0]
# [ 4 5896 6 75 8 0 8 0 3 0]
# [ 92 6 5002 76 565 1 232 1 25 0]
# [ 191 49 23 5504 162 1 61 0 7 2]
# [ 15 12 267 213 5305 1 168 0 19 0]
# [ 0 0 0 0 0 5847 0 112 3 38]
# [1159 16 523 189 676 0 3396 0 41 0]
# [ 0 0 0 0 0 99 0 5540 0 361]
# [ 28 6 29 15 32 23 26 14 5827 0]
# [ 0 0 0 0 1 61 0 107 1 5830]]
- 水平轴:预测标签(类)
- 真实标签
- 热图值(颜色)
预测标签和真标签显示了我们正在处理的预测类。矩阵对角线表示矩阵中预测和真相相同的位置,所以这是我们希望热图更暗的地方。
任何不在对角线上的值都是不正确的预测,因为预测和真实标签不匹配。如果想知道更多的细节,我们可以使用以下步骤: - 在水平轴上选择一个预测标签。
- 检查该标签的对角线位置,查看总数是否正确。
- 检查其他非对角位置,查看网络混乱的位置。
例如,网络将T-shirt/top与 shirt混淆,但不会将T-shirt/top与以下内容混淆: - Ankle boot
- Sneaker
- Sandal
随着我们的模型的学习,我们将看到对角线之外的数字变得越来越小。