条件随机场（CRF）极简原理与超详细代码解析

CRF是一个非常经典的图模型，网上关于CRF的详细介绍也很多，但本文不会针对原理做很多介绍和推导，我也不是很擅长这方面，而是从NLP应用的角度，以经典的LSTM-CRF或BERT-CRF等 序列标注模型为切入点，介绍CRF模型是怎样用pytorch实现的，以及在实现的过程中，CRF模型到底在做什么。

如果你符合以下情况之一，那么我认为此文适合你阅读：

1. 刚接触NLP任务，对序列标注模型有大概的理解，但不是很熟练；
2. 已经做NLP很久了，但是每次建模都是调包导模型，并不清楚模型是怎样运作的；
3. 概率论学的不是很好，不想看公式；
4. 看过很多关于CRF的介绍文章，当时懂了，回头又忘记CRF是怎么回事儿。

本文将以pytorch版本CRF的一个实现为例，尽可能详细地说明CRF是怎样实现的，对代码的解释几乎精细到每一行，相信你耐心读完本文，会从实践的角度对CRF的理解更加深刻。

1. 原理

尽管在使用CRF时，好像很简单，只需要实例化一个crf对象，然后把它拼接在特征抽取模型之后就可以了，但是说起CRF的原理，推导起来还比较复杂，多数介绍理论的文章会从图模型说起，讲到马尔可夫模型，最后再讲到CRF。但是本文是一篇偏向实践的介绍，在这里介绍原理，也只是为了更好地理解代码，所以我会说的非常简略。并且，我个人理解可能不是特别透彻，如果有讲的不准确的地方，还请路过的大佬们帮忙指正。

1.1 从名称说起

CRF全称Conditional Random Field，条件随机场，本质上是一个无向图模型，其中的“随机”，可以理解为图中的每个节点，都是一个随机变量。对于我们常提起的条件随机场模型，其实指的是狭义的线性条件随机场，我们有两组随机变量X和Y，其中Y是我们所关心的目标变量，X是可以直接获取到的观测变量。

同时也是马尔可夫随机场的一个特例，具备马尔可夫性。说起马尔可夫性，直观的理解就是，图上的每个节点的分布，只与它相邻的节点的分布有关。对于线性、有向的条件随机场来讲，也就是每一个目标变量$y_i$，只会受到它的上一个变量$y_{i-1}$的影响。

但真实世界中，这种假设，有点难以满足。刚才的假设，是只看目标变量Y的情况下，但实际情况下，Y会受到外界因素X的影响，例如，我们关心一个孩子10岁能长多高，除了需要知道他9岁的时候长了多高之外，我们还希望知道他吃的好不好，营养能不能跟得上。这也就是条件随机场中的“条件”，即CRF是对P(Y|X)进行建模的。

1.2 优化的目标

在序列标注任务中，CRF是一个链式的模型。假设我们有一个长度为seq_len的序列，我们希望把序列中的每一个token，预测它的类型，所以我们的目标可以看做是获取一个(seq_len, num_labels)的矩阵，进而可以把问题看做是一个找正确路径的问题。

假设有一个人，要从序列的开始位置走到序列的结束位置，对于每一个位置，都可以取num_labels个格子可以走，但是其中每次只有一个格子是正确的格子。那么最终可以组合出来的路径总数，一共有seq_len ** num_labels种，这其中，有一条路径，是正确的路径（也就是每个位置上的label全都预测正确），我们希望这个人，尽量能找到正确的那条路径（注意，我们关心的是尽量让每个位置的label都找正确，而不仅仅是最后的结束位置的label正确）。

假设深色的格子是每一步中正确的label，则途中红色的路径就是正确的路径。

假如每一条路径都有一个得分$p$，第$k$条路径的得分为$p=e^{s_k}$，我们的目标就是正确的那一条路径的得分$p_{real}$，越大越好，为了消除分数的量纲，我们的目标确定为：

$$Prob=\frac{e^{p_{real}}}{e^{p_1}+e^{p_2}+...+e^{seqlen\ast numlabels}}$$

在上图的例子中，总共有$3^3=27$种路径，分母就一共有27项。

我们希望真实路径的得分越大越好，所以上式取负对数，就可以作为损失函数：
$$Loss=-{\log }_{}Prob=\log (e^{p_1}+e^{p_2}+...+e^{seqlen\ast numlabels})-P_{real}$$

对于每一条路径的得分，定义发射得分和转移得分，

• 发射得分 $e{m}_{t,i}$：第i个token的label的index是t的得分；
• 转移得分 $t{r}_{t_1,t_2}$：上一个token，label index是$t_1$，当前token的label index是$t_1$的得分。

1.3 如何计算

从损失函数的构成可以看到，有两部分需要计算，一是真实路径的得分，二是达到该点的所有路径的总分。
其中真实路径的得分，我们可以直接根据真实的label，分别计算出发射得分和转移得分，然后将这两项相加即可。
而所有路径的得分之和$\log (e^{p_1}+e^{p_2}+...)$，如果计算每一条路径的得分，然后加起来的话，复杂度太高了，实际情况下，会采取动态规划的技巧。

假设用$P_{i,t}$表示$t$时刻，label index为$i$的logsumexp形式的所有路径的得分之和，那么我们想要求个多有路径得分的总和，就是$i$取所有情况时的结果之和：
$$\log (e^{p_1}+e^{p_2}+...)=P_{1,seqlen}+P_{2,seqlen}+...+P_{numlabels,seqlen}$$

我们在seq_len的维度上，也就是对时刻t，做动态规划：对于某个时刻$t$，可以由上一个时刻$t-1$转移得到这个时刻的总分。

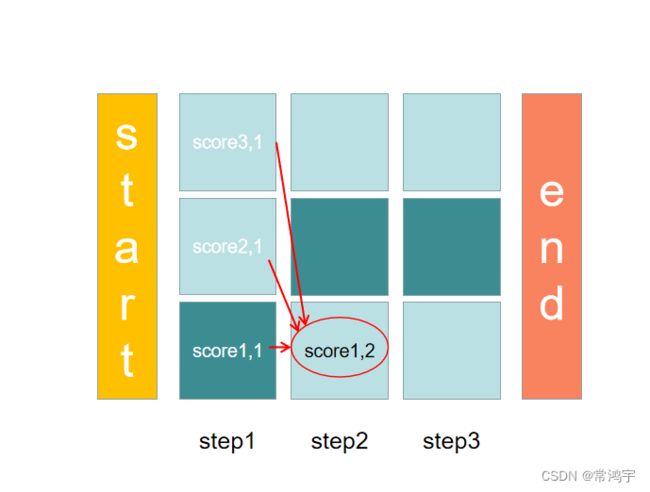
每一步的全部得分，都可以从它上一步的所有可能的得分转移得到，由此来实现状态转移。

具体而言，反应在公式上就是：
假如这个时刻的label index是1，它上一个时刻的label index 也是1，那么有：
$$P_{1,t-1}\to P_{1,t}=P_{1,t-1}+e{m}_{t,1}+t{r}_{1,1}$$
同理，当它上一个时刻的label index是2时：
$$P_{2,t-1}\to P_{1,t}=P_{2,t-1}+e{m}_{t,1}+t{r}_{2,1}$$
于是，上一个节点的label是对于num_labels（简写为$m$）中的每一种情况，我们令：
$$Q_1=P_{1,t-1}+e{m}_{t,1}+t{r}_{1,1}$$
可以从1写到$m$（label的总数）：

$$Q_m=P_{m,t-1}+e{m}_{t,1}+t{r}_{m,1}$$
（从上式我们可以看到，num_labels这一维度，只影响到了上一个时刻的得分，以及转移得分，对发射得分没有影响。）

于是由$P_{i,t}$的定义可以得到，
$$P_{1,t}=\log (e^{Q_1}+e^{Q_2}+...+e^{Q_m})\text{\hspace{1em}(*)}$$
这是我们考虑$i=1$的情况时，那么对于时刻$t$，一共有$m$个label，同样的式子我们就可以写$m$个。到这里，最终的解法也就呼之欲出了。

我们维护一个previous矩阵，它的每一行考虑了上一个状态的每一种情况时的得分，然后重复了$m$行：
$$\left(\begin{array}{cccc}{P}_{1,t-1},& P_{2,t-1},& ...,& P_{m,t-1}\\ ...& ...& ...& ...\\ P_{1,t-1},& P_{2,t-1},& ...,& P_{m,t-1}\end{array}\right)$$

以及发射矩阵：
$$\left(\begin{array}{cccc}e{m}_{t,1},& e{m}_{t,1},& ...,& e{m}_{t,1}\\ e{m}_{t,2},& e{m}_{t,2},& ...,& e{m}_{t,2}\\ ...& ...& ...& ...\\ e{m}_{t,m},& e{m}_{t,m},& ...,& e{m}_{t,m}\end{array}\right)$$

以及转移矩阵：
$$\left(\begin{array}{cccc}t{r}_{1,1},& t{r}_{2,1},& ...,& t{r}_{m,1}\\ t{r}_{1,2},& t{r}_{2,2},& ...,& t{r}_{m,2}\\ ...& ...& ...& ...\\ t{r}_{1,m},& t{r}_{2,m},& ...,& t{r}_{m,m}\end{array}\right)$$

现在把这三个矩阵的对应位置的元素相加，就得到了我们刚刚定义的$Q$的矩阵，
$$\left(\begin{array}{cccc}{Q}_{1,1},& Q_{1,2},& ...,& Q_{1,m}\\ ...& ...& ...& ...\\ Q_{m,1},& Q_{m,2},& ...,& Q_{m,m}\end{array}\right)$$

由(*)式我们可以得到，$Q$矩阵的每一行，取logsumexp就是一个路径得分之和$P$，第一行的logsumexp就是$P_{1,t}$，以此类推。这样$m$行都取logsumexp，然后转置，恰好就得到了
$$[P_{1,t},P_{2,t},...,P_{m,t}]$$

我们对这个东西求和，也就是我们要求的就是t时刻所有路径的得分之和（优化目标的分母）。

并且，把这个行复制$m$份，拼起来的新的矩阵，刚好就是下一个时刻$t+1$对应的prev矩阵：
$$\left(\begin{array}{cccc}{P}_{1,t},& P_{2,t},& ...,& P_{m,t}\\ ...& ...& ...& ...\\ P_{1,t},& P_{2,t},& ...,& P_{m,t}\end{array}\right)$$

至此，某时刻的所有路径得分之和的动态规划解法，就介绍完了，如果有同学觉得这样讲的不是很详细，可以参考这篇推送。

2. 代码

crf的pytorch实现有很多很多版本，在之前的博客中，我们简单介绍了torchcrf中的代码，但是这篇博客不再沿用之前的那一版代码进行介绍，而是采用另一个版本（多看不同版本的代码有助于加深理解）。

这个版本的代码其实是一种mask的CRF，也就是说，对所有非法的路径进行了mask，例如，从B-PER到I-LOC的转移。下面的代码中会涉及到mask，所以提前说明一下。

这一版本的CRF实现，是从经典的信息抽取模型OneIE的开源代码中粘出来的，我不确定这个代码是来自其他开源项目，还是该项目原创，总之我们现在有这样一套代码，接下来让我们一步步弄清楚在这段代码里边发生了什么。

2.1 基本结构

首先我们从整体的角度看一下代码结构，可以分为三个部分：

• 初始化
• 计算得分
• viterbi解码

下面是代码基本结构：

class CRF(nn.Module):
    def __init__(self, label_vocab, bioes=False):
        super(CRF, self).__init__()
        pass

	def initialize(self):
		"""初始化转移矩阵"""
		pass

	@staticmethod
    def pad_logits(logits):
    	"""辅助padding方法"""
    	pass
	
	# 以下5个方法用来在训练过程中计算得分
	def calc_binary_score(self, labels, lens):
		"""计算转移得分"""
		pass

	def calc_unary_score(self, logits, labels, lens)
		"""计算发射得分"""
		pass

	def calc_gold_score(self, logits, labels, lens):
		"""获取正确得分"""
		pass

	def calc_norm_score(self, logits, lens):
		"""计算所有路径得分"""
		pass

	def loglik(self, logits, labels, lens):
		"""计算损失"""
		pass

	# viterbi解码
	def viterbi_decode(self, logits, lens):
		pass

作为一个记录了节点状态的过程，CRF其实并不算复杂，我们需要注意的特征维度其实只有两个，标签数量m，以及状态节点的总数n，然后在实际使用中，通常还有一个batch size：

• batch_size: 训练的批次，下文的介绍中为了简单起见我们通常假设它为1；
• num_labels: 也就是标签数量m，序列每个位置上的label可能的取值，例如只有一个实体的BIO标注的情况下，m=3（B, I, O），如果是BIOES标注，则m=5；
• seq_len: 序列的长度n。

在正式开始之前，还是要唠叨一句，看代码的过程中一定要有维度的意识，这对我们理解代码是如何操作的非常重要，在下文中，我把所有的维度信息全都高亮了，以引起大家的注意。接下来我们将逐步拆解每一部分代码。

2.2 模型初始化

我们知道，在一个线性的CRF中，每一个节点的状态由它上一个节点的状态以及输入x计算获得：

• 对于BERT-CRF模型，输入x是由BERT编码得到的特征，相对CRF模型来讲可以看做是外部输入，所以在构建CRF模型本身时，我们并不需要在类中维护这样一个变量，只需要将它以数据流的形式参与计算即可。
• 而节点与节点之间的状态转移，则是CRF模型内部的，需要在训练的过程中对其进行维护，它的内容是每一个label到另一个label（包括其自身）的得分，所以我们需要维护一个尺寸为[num_labels, num_labels]的一个矩阵。

模型的初始化部分包括了__init__和initialize。

需要注意的是，CRF的整个路径的长度，与待标注的序列的长度其实是不一样的，多了一个开始标记位和一个结束标记位，这就造成了转移矩阵的尺寸需要加2，所以准确地说，我们的状态转移矩阵的尺寸应该是[num_labels+2, num_labels+2]，并且拿到bert编码输出之后，传入CRF之前，需要一个额外的padding操作，我们把padding的方法pad_logits也放在初始化这部分中讲。

具体的解释详见下面代码中的注解。

class CRF(nn.Module):
    def __init__(self, label_vocab, bioes=False):
    	"""
		:param label_vocab: Dict: 每个label对应的idx，例如{"O": 0, "B-PER": 1, ...}
		:param bioes: bool: 是bioes形式的标注还是bio形式的标注，默认bio
		整个初始化过程其实就是创建了一个状态转移矩阵transition
		"""
        super(CRF, self).__init__()

        self.label_vocab = label_vocab
        self.label_size = len(label_vocab) + 2                         # 增加了和
        self.bioes = bioes

        self.start = self.label_size - 2                               # 倒数第2个label是
        self.end = self.label_size - 1                                 # 倒数第1个label是
        transition = torch.randn(self.label_size, self.label_size)     # 初始化一个(num_labels+2, num_labels+2)的矩阵
        self.transition = nn.Parameter(transition)                     # 将状态转移矩阵转化为可训练参数
        self.initialize()

    def initialize(self):
    	"""
    	对转移矩阵进行进一步操作，将所有必然不可达的状态都设置为一个默认值-100
		注意第一个axis是to_label, 第二个axis才是from_label
		"""
        self.transition.data[:, self.end] = -100.0                     # 不可以向任何一个label转移
        self.transition.data[self.start, :] = -100.0                   # 没有任何一个label可以转移到

		# 对num_labels两层遍历，排除所有不合理的情况
        for label, label_idx in self.label_vocab.items():              # ("O": 0), ("B-PER": 1), ...
            if label.startswith('I-') or label.startswith('E-'):       # 不能跳过B直接转移到I和E
                self.transition.data[label_idx, self.start] = -100.0
            if label.startswith('B-') or label.startswith('I-'):       # 不能由B或I转移得到（这是BIOES的规则）
                self.transition.data[self.end, label_idx] = -100.0

        for label_from, label_from_idx in self.label_vocab.items():
            if label_from == 'O':
                label_from_prefix, label_from_type = 'O', 'O'
            else:
                label_from_prefix, label_from_type = label_from.split('-', 1)

            for label_to, label_to_idx in self.label_vocab.items():
                if label_to == 'O':
                    label_to_prefix, label_to_type = 'O', 'O'
                else:
                    label_to_prefix, label_to_type = label_to.split('-', 1)

                if self.bioes:
                	# 1. 如果是BIOES形式，则
                	# 1) [O, E, S]中的任意一个状态，都可以转移到[O, B, S]中任意一个状态，不论前后两个状态的label是否相同
                	# - 例如，可以从E-PER转移到B-LOC
                	# 2) 当label相同时，允许B->I, B->E, I->I, I->E
                	
                    is_allowed = any(
                        [
                            label_from_prefix in ['O', 'E', 'S']
                            and label_to_prefix in ['O', 'B', 'S'],

                            label_from_prefix in ['B', 'I']
                            and label_to_prefix in ['I', 'E']
                            and label_from_type == label_to_type
                        ]
                    )
                else:
                	# 2. 如果是BIO形式，则
                	# 1) 任何一个状态都可能转移到B和O
                	# 2) I状态只能由相同label的B或者I得到
                    is_allowed = any(
                        [
                            label_to_prefix in ['B', 'O'],

                            label_from_prefix in ['B', 'I']
                            and label_to_prefix == 'I'
                            and label_from_type == label_to_type
                        ]
                    )
                if not is_allowed:
                    self.transition.data[label_to_idx, label_from_idx] = -100.0

下面是padding的方法，其实就是给logits在第axis=2上添加了一个sos和一个eos，并且把序列的所有位置的sos和eos的概率全都设置为-100：

    @staticmethod
    def pad_logits(logits):
        """Pad the linear layer output with  and  scores.
        :param logits: Linear layer output (no non-linear function).
        """
        batch_size, seq_len, _ = logits.size()                     # (batch, seq_len, num_labels)
        pads = logits.new_full((batch_size, seq_len, 2), -100.0,   
                               requires_grad=False)                # 返回一个形状为(batch, seq_len, 2)的tensor，所有位置填充为-100
        logits = torch.cat([logits, pads], dim=2)                  # 拼接得到(batch, seq_len, num_labels+2)
        return logits

经过上面的变化，我们就可以实现BERT输出的logits与CRF中转移矩阵的尺寸对应了。

2.3 BERT提取的特征如何输入给CRF

在展开计算得分的介绍之前，我们需要先搞明白，CRF与我们的特征提取模型（BERT编码器）是如何进行交互的。
假如我们有一个用transformers创建的BERT模型：

from transformers import BertModel, BertTokenizer
bert = BertModel.from_pretrained('bert-base-uncased')
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')

然后我们对输入进行tokenize之后，得到input_ids和attention_mask，然后把它们传给模型。

text = 'your text here.'
inputs = tokenizer(text)
bert_out = bert(inputs['input_ids'], attention_mask=inputs['attention_mask'])[0]

对这一块不熟悉的同学可以先去学一下transformers模块。
我们这里拿到的bert_out，是一个尺寸为(batch, seq_len, hidden)的tensor，

到这里还不够，细心的同学可能已经发现，在前文的维度介绍中，并没有bert的hidden_size这个尺寸，CRF关心的是每个token被分为每个label的概率，并不关心bert所定义的向量空间，所以需要用一个linear层把它干掉。

import torch.nn as nn
label_ffn = nn.Linear(bert_hidden_size, num_labels, bias=True)
label_scores = label_ffn(bert_out)

经过这样的一个线性变换，我们得到的label_scores，也就是输入给CRF的外部特征x序列，尺寸就变成了(batch, seq_len, num_labels)。

然而，我们刚刚也说了label_scores的尺寸中是num_labels，而CRF中需要的是num_labels+2，所以我们利用刚才的padding方法，进行转换：

crf = CRF(vocab)   # 这里实例化一个CRF类，目的是利用它的padding方法
label_scores = crf.pad_logits(label_scores)

于是现在label_scores的尺寸变成了CRF所需要的(batch, seq_len, num_labels+2)。

万事俱备，只差CRF。

2.4 计算得分

2.4.1 CRF的输入与计算逻辑

终于到了CRF的核心部分。接着2.3节中的内容，我们看一下crf计算损失的总控函数是怎样的。在这一版的代码中，CRF.loglik就是这个总控方法，其调用时传入的参数如下：

label_loglik = crf.loglik(label_scores,
                          label_idxs,
                          token_nums)

• label_scores: 上文所述的每个位置上每个label得分，(batch, seq_len, num_labels+2);
• label_idxs: 每个位置上正确的label index，(batch, seq_len);
• token_nums: batch中每个序列的token数量，(batch).

为了更好地帮助读者理解，我们举一个例子：
假如我们有一个序列（简单起见不考虑[CLS], [SEP]和subword分词）：

['Tom', 'went', 'to', 'New', 'York', '.']

我们的label是BIO的形式标注的两类实体，PER和LOC，那么所有label为：

['O', 'B-PER', 'I-PER', 'B-LOC', 'I-LOC']

以及label对应的vocab：

{'O': 0, 'B-PER': 1, 'I-PER': 2, 'B-LOC': 3, 'I-LOC': 4}

那么，我们需要输入CRF的label_scores就是一个(1, 6, 5)的tensor，
对应的label_idxs是一个(1, 6)的tensor，它应该是：

tensor([[1, 0, 0, 3, 4, 0]])
# PER, O, O, LOC, LOC, O

以及token_nums是一个(batch)的tensor，它应该是：

tensor([6])

至于它们三个分别是干什么用的，到了具体的计算中自然就清楚了。

说回我们的总控方法：

    def loglik(self, logits, labels, lens):
        norm_score = self.calc_norm_score(logits, lens)          # 全部路径的得分总和
        gold_score = self.calc_gold_score(logits, labels, lens)  # 由正确的label计算出来的得分
        return gold_score - norm_score

这一部分就很清楚地写出了CRF的训练目标，
$$Loss=-{\log }_{}Prob=\log (e^{p_1}+e^{p_2}+...+e^{seqlen\ast numlabels})-P_{real}$$

但是这个loglik中跟损失函数实际上是反着的，所以在优化这个损失的时候，记得给它取负号。

2.4.2 计算真实得分

在loglik中我们看到，CRF的训练目标，是gold_score与norm_score之间的差值，我们希望这两部分尽量接近，也就是真实路径的得分所占全部路径得分之和的比值尽可能大。

那么gold_score，也就是真实得分，是怎么来的呢，它由发射得分和转移得分两部分构成：

    def calc_gold_score(self, logits, labels, lens):
        """计算真实得分"""
        unary_score = self.calc_unary_score(logits, labels, lens).sum(1).squeeze(-1)
        binary_score = self.calc_binary_score(labels, lens).sum(1).squeeze(-1)
        return unary_score + binary_score

接下来的2.4.2.1和2.4.2.2两节中，将详细介绍发射得分和转移得分是怎么来的。

2.4.2.1 计算发射得分

发射得分，是由外部输入x得到的，有些人也习惯称其为Unigram得分，因为只考虑了x这一项（与此同时，转移得分也称作Bigram，因为同时考虑了y_i和y_i-1）。

发射得分的代码是这样写的：

    def calc_unary_score(self, logits, labels, lens):
        """
        计算发射得分
        logits: (batch, seq_len, num_labels+2)
        labels: (batch, seq_len)
        lens: (batch)
        """
        labels_exp = labels.unsqueeze(-1)
        scores = torch.gather(logits, 2, labels_exp).squeeze(-1)
        mask = sequence_mask(lens).float()
        scores = scores * mask
        return scores

可以看到它把三项输入全都用上了。
这个方法的核心就是一个torch.gather()，具体而言，就是对根据一个idx tensor，对目标tensor取值，然后再拼接再一起。

• 其中第一个参数logits，是目标tensor，也就是说，gather返回的值，是从这个tensor中取出来的；
• 第二个参数2，意思是在哪一个维度上进行操作，我们知道logits有0, 1, 2三个维度，这里的2意思就是在维度2，也就是num_labels+2的那个维度上进行操作；
• 第三个参数label_exp，是告诉gather方法，在取值的时候怎么取。

由于torch.gather要求idx tensor和目标tensor的维度是一样的，而labels相比logits少了一个维度，所以我们需要先对它unsqueeze出一个维度。

简便起见，我们忽略batch维度，假设输入的logits是这样的：

# logits: (seq_len, num_labels+2)
tensor([[-3.5,   7.1,   6.9,   -5.4,   2.0,   -8.7,   -1.9],
        [15.7,   -4.2,   6.6,  -5.3,  -11.9,  -2.2,   2.3],
        ...])

假设输入的label，在忽略batch，并且unsqueeze之后，是这样的：

# labels: (seq_len, 1)
tensor([[1],
        [0],
        ...,])

那么gather之后的结果就是这样的（同样是忽略batch）：

# scores: (seq_len, 1)
tensor([[7.1],
        [15.7],
        ...])

也就是logits中的第0行，根据label的第0行，取了第1个元素，logits的第1行，根据label的第1行取了第0个元素，……，然后再把取完之后的结果拼起来，具有形状(batch, seq_len, 1)，最后在squeeze掉最后一个维度，就是我们需要的scores了，形状是(batch, seq_len)。

然后要进行mask，这个sequence_mask是一个辅助函数，定义如下：

def sequence_mask(lens, max_len=None):
    """Generate a sequence mask tensor from sequence lengths, used by CRF."""
    batch_size = lens.size(0)
    if max_len is None:
        max_len = lens.max().item()
    ranges = torch.arange(0, max_len, device=lens.device).long()
    ranges = ranges.unsqueeze(0).expand(batch_size, max_len)
    lens_exp = lens.unsqueeze(1).expand_as(ranges)
    mask = ranges < lens_exp
    return mask

这个方法很简单，就是根据一个batch生成一个mask tensor，举个例子，如果你的batch_size=4，序列的长度分别为3，5，2，6,那么生成的mask矩阵就是一个形状为(batch, max_seq_len)的tensor：

tensor([[True,  True,  True, False, False, False],
        [True,  True,  True,  True,  True, Flase],
        [True,  True, False, False, False, False],
        [True,  True,  True,  True,  True,  True]])

将mask作用在scores上，就实现了对scores的padding部分（注意这里说的padding是序列长度方向上的padding，不是上文padding函数的num_labels方向上的padding，因为到这里num_labels这个维度已经被gather掉了）的mask。

以上就是ugram特征（发射得分）的计算过程，最终我们得到的scores是形状是(batch, seq_len)，还是比较容易理解的。

趁热打铁，我们来直观地理解一下这个发射得分是什么东西。回顾一下这个计算过程，首先我们利用BERT编码器，获取到了batch中每个instance的token的特征（(batch, seq_len, hidden)），然后我们利用一个Linear层，将每个token上的特征，转化成了在label空间上的logits（(batch, seq_len, num_labels+2)），这一步的结果，可以理解为，每个token属于某一类label的“概率”。

我们知道，CRF是一个判别模型，所以直观地理解，我们希望这个模型“更准确”，那么就是希望对于某一个token，能够以更大的“概率”，将其判断为正确的label，所以自然地，在我们知道label的情况下，把所有正确label位置上的得分都取出来，就是整个序列的发射得分，我们希望它尽可能大。
（TODO: 类别加权算分）

2.4.2.2 计算转移得分

如2.2节中所述，转移得分的计算与发射得分不同，是需要用到CRF类的transition矩阵的（刚刚的calc_unary_score放到CRF类里，在pycharm中会有黄色的波浪线，因为它是静态方法）。

需要注意的是，既然是状态转移“矩阵”，那就是涉及到两个方向的，所以num_labels维度和seq_len维度在这一部分中都需要注意。

为了方便说明转移得分的计算过程，我们还是以之前的例子，两类实体BIO格式标注，共有5个label，那么，加上sos和eos两个额外的label，一共就是7个label，其中每个label对应的idx如下：

• ‘O’: 0
• ‘B-PER’: 1
• ‘I-PER’: 2
• ‘B-LOC’: 3
• ‘I-LOC’: 4
• ‘sos’: 5
• ‘eos’: 6

为了与前文保持统一，仍然称真实的label数量为num_labels（5），添加了开始和结束位的数量为num_labels+2（7）。

这一部分可能有点绕，但是别慌，跟着下面的思路走，理解应该不成问题。先把注解版的代码贴在下面，然后我们一段一段的讲这部分代码。

    def calc_binary_score(self, labels, lens):
        """
        计算转移得分
        :param labels: (batch, seq_len)
        :param lens: (batch)
        :return:
        """
        batch_size, seq_len = labels.size()

        # 1. 扩展label：其实就是对labels在seq_len的维度上扩展了一个开头和末尾
        # A tensor of size batch_size * (seq_len + 2)
        labels_ext = labels.new_empty((batch_size, seq_len + 2))             # 生成一个(batch_size, seq_len + 2)没有初始化的tensor
        labels_ext[:, 0] = self.start                                        # batch中每个instance的第1个位置的值变成start（label_size -2)
        labels_ext[:, 1:-1] = labels
        mask = sequence_mask(lens + 1, max_len=(seq_len + 2)).long()         # 开头start位置为True，后边true部分每一位向后移动一位
        pad_stop = labels.new_full((1,), self.end, requires_grad=False)      # (batch)， 以eos生成一个tensor([6,...,6])
        pad_stop = pad_stop.unsqueeze(-1).expand(batch_size, seq_len + 2)    # (batch) -> (batch, seq_len+2)
        labels_ext = (1 - mask) * pad_stop + mask * labels_ext               # 被mask的部分变成6，剩下的部分是正确的label
        labels = labels_ext

        # 2. 扩展transition：复制了batch份，另batch中的每个instance都有一个transition矩阵
        trn = self.transition                                                # 注意，self.transition的行是from_label, 列是to_label
        trn_exp = trn.unsqueeze(0).expand(batch_size, self.label_size,
                                          self.label_size)
        
        # 接下来两部分是重点，计算了从一个label转移到另一个label的得分
        # 3. to_label的得分计算
        lbl_r = labels[:, 1:]  # 在原始的seq_len上去掉了第一个token
        lbl_rexp = lbl_r.unsqueeze(-1).expand(*lbl_r.size(), self.label_size)  # (batch, seq_len+1) -> (batch, seq_len+1, num_labels)
        # score of jumping to a tag
        # 取trn_exp的lbl_rexp中对应的一行（也就是取真实label对应的转移），然后拼起来
        # (batch, num_labels+2, num_labels+2) -> (batch, seq_len-1, num_labels+2)
        trn_row = torch.gather(trn_exp, 1, lbl_rexp)                         # 这个就是每一个token上，由某个label转移到当前label的得分

        # 4. from_label的得分计算
        lbl_lexp = labels[:, :-1].unsqueeze(-1)                              # (batch, seq_len+1, 1)  每个位置是从哪个label转移来的
        trn_scr = torch.gather(trn_row, 2, lbl_lexp)                         # (batch, seq_len+1, 1)  from_label到to_label的真实得分
        trn_scr = trn_scr.squeeze(-1)                                        # (batch, seq_len+1, 1) -> (batch, seq_len-1)

        # 5. mask掉seq_len维度上的start，注意不是mask掉num_labels上的start
        mask = sequence_mask(lens + 1).float()
        trn_scr = trn_scr * mask
        score = trn_scr

        return score

我们把这部分代码拆解成五个部分，

§ 第一部分

第一部分是将labels做了一个扩展，看似很简单，但是第一眼看过去可能有点疑惑，这么做的目的是什么，
其实是为这个函数的核心思想——错位——做准备。

        # 1. 扩展label：其实就是对labels在seq_len的维度上扩展了一个开头和末尾
        # A tensor of size batch_size * (seq_len + 2)
        labels_ext = labels.new_empty((batch_size, seq_len + 2))             # 生成一个(batch_size, seq_len + 2)没有初始化的tensor
        labels_ext[:, 0] = self.start                                        # batch中每个instance的第1个位置的值变成start（label_size -2)
        labels_ext[:, 1:-1] = labels
        mask = sequence_mask(lens + 1, max_len=(seq_len + 2)).long()         # 开头start位置为True，后边true部分每一位向后移动一位
        pad_stop = labels.new_full((1,), self.end, requires_grad=False)      # (batch)， 以eos生成一个tensor([6,...,6])
        pad_stop = pad_stop.unsqueeze(-1).expand(batch_size, seq_len + 2)    # (batch) -> (batch, seq_len+2)
        labels_ext = (1 - mask) * pad_stop + mask * labels_ext               # 被mask的部分变成eos的idx，剩下的部分是正确的label
        labels = labels_ext

这几行其实就是在seq_len的维度上加了2，从形状为(batch, seq_len)的labels，生成了一个扩展的形状为(batch, seq_len+2)的label_ext。
细心的同学可能发现了，之前我们+2，增加的sos和eos位置，那不是在num_labels的维度上加的吗，意思是标记状态转移的开始和结束，现在怎么又加在seq_len维度上了，这不就乱了吗？其实这两者正好是对应的，也就是我们在开始之前有一个虚拟的开始位置，它的label是sos，结束之后有一个结束位置，label是eos。

说回错位的思想：

由CRF的（条件）马尔可夫性可知，某一个时刻的状态，除了受外界条件（输入x，也就是发射得分的部分）影响之外，只受它的前一时刻的状态影响，所以理论上我们需要两个label序列，一个from序列，和一个to序列。但是对于label来讲，两个序列其实是共享的，他们之间只差了一个时间步（也就是在seq_len维度上），所以我们没有必要做两条label序列出来，而是给它做长一点就可以了：

生成一个label_ext，使得取[:, 1:]时，获取的是to序列的label，取[:, :-1]时，获取的是from序列的label。
具体是怎么操作的呢，还是假设batch_size是1，假如我们的label原本是这个样子：

[[1, 0, 0, 3, 4, 0]]
# [[B-PER, O, O, B-LOC, I-LOC, O]]

经过前三行之后，就变成了：

[[5, 1, 0, 0, 3, 4, 0, ?]]
# [[sos, B-PER, O, O, B-LOC, I-LOC, O, empty]]

然后生成了一个mask，mask跟之前的mask相比，其实就是对batch中的每一个instance，在第一个1之前又加了一个1。于是我们有mask：

[[1., 1., 1., 1., 1., 1., 1., 0.]]

再然后，以eos（idx=6）做了一个用来pad_stop，形状为(batch, seq_len+2)，其中的内容全都是eos对应的idx，也就是6.，然后把这个结合mask作用在label_ext上，也就是所有被mask的位置的label，变成eos的idx，其余位置保留。

折腾了一大圈下来，我们的label_ext也就变成了：

[[5, 1, 0, 0, 3, 4, 0, 6]]

假如我们的batch_size不是1，还有另外一句话，“Tom is cool.”，那生成的label_ext，可能是这个样子：

[[5, 1, 0, 0, 3, 4, 0, 6],
 [5, 1, 0, 0, 0, 6, 6, 6]]

§ 第二部分

第二部分是扩展转移矩阵transition

        # 2. 扩展transition：复制了batch份，另batch中的每个instance都有一个transition矩阵
        trn = self.transition                                                # 注意，self.transition的行是from_label, 列是to_label
        trn_exp = trn.unsqueeze(0).expand(batch_size, self.label_size,       # 这里的self.label_size就是一直强调的num_labels+2
                                          self.label_size)

这部分很容易理解，就是在batch维度上复制，相当于给了batch中的每一个instance都有一个转移矩阵，扩展之后的trn_exp的形状为(batch, num_labels+2, num_labels+2)。

需要注意的是，self.transition的两个num_labels+2的维度，是to在前，from在后，如果这里没有注意到，后边的代码可能就优点困惑了。详见2.2节中的初始化部分。

§ 第三部分

第三部分计算是to label，得到的是：
“假如我们知道当前位置的label，从上一个位置的每一个label转移过来的得分”

可能比较拗口，下面根据代码解释一下：

        # 3. to_label的得分计算
        lbl_r = labels[:, 1:]  # 在原始的seq_len上去掉了第一个token
        lbl_rexp = lbl_r.unsqueeze(-1).expand(*lbl_r.size(), self.label_size)  # (batch, seq_len+1) -> (batch, seq_len+1, num_labels)
        # score of jumping to a tag
        # 取trn_exp的lbl_rexp中对应的一行（也就是取真实label对应的转移），然后拼起来
        # (batch, num_labels+2, num_labels+2) -> (batch, seq_len+1, num_labels+2)
        trn_row = torch.gather(trn_exp, 1, lbl_rexp)                          # 这个就是每一个token上，由某个label转移到当前label的得分

代码第一行：如第一部分中所述，我们对labels取[:, 1:]时，获取的是to序列的label
代码第二行：扩展出一个维度，(batch, seq_len+2-1) 扩展为 (batch, seq_len+2-1, num_labels)
代码第三行：以to label（每个位置上的真实label）为标准，在转移矩阵的维度1（num_labels+2的维度上），取相应的行拼在一起，得到一个形状为(batch, seq_len+1, num_labels+2)的tensor trn_row。

具体的，在不考虑batch的情况下，假如我们在第二部分中扩展trn_ext是这个样子（实际不会是这样样子，这样写为了方便理解gather）：

tensor([[0, 0, 0, 0, 0, 0, -100],
        [1, 1, 1, 1, 1, 1, -100],
        [2, 2, 2, 2, 2, 2, -100], 
        ...,])

gather之后的trn_row就是分别取了to label对应的每一行，然后再拼起来，也就是：

tensor([[5, 5, 5, 5, 5, 5, -100],
        [1, 1, 1, 1, 1, 1, -100],
        [0, 0, 0, 0, 0, 0, -100],
        ...])

再强调一遍，trn_row中的每一行，不会是像 [1, 1, 1, 1, 1, 1, -100]，它的实际意义是，每一个token（列的方向上），由上一个token的每一种可能的label（行的方向上），转移到当前label的得分。也就是说，这一步的计算，固定了to label，而没有固定from label。

每一行中，指的是上一个token的label，而不是当前这个token的label。所以我们看到，任意一行，最后一个元素一定是-100，因为不可能出现“上一个token是eos”的状况。

§ 第四部分

第四部分计算的是from label

得到的是：当上一个token的label是$labe{l}_i$时，转移到当前token的label是$labe{l}_j$的得分。

理解了第三部分之后，第四部分就相对容易理解了。刚才说了，第三部分中只确定了当前token的label，而上一个token的label是任意的，第四部分就是把上一个token的label也确定下来，这样就得到了在当前的转移矩阵下，真实情况下的从label_i转移到label_j的转移得分。

        # 4. from_label的得分计算
        lbl_lexp = labels[:, :-1].unsqueeze(-1)                              # (batch, seq_len+1, 1)  每个位置是从哪个label转移来的
        trn_scr = torch.gather(trn_row, 2, lbl_lexp)                         # (batch, seq_len+1, 1)  from_label到to_label的真实得分
        trn_scr = trn_scr.squeeze(-1)                                        # (batch, seq_len+1, 1) -> (batch, seq_len-1)

第一行代码：取label的左移部分，模拟的是上一个token的label；
第二行代码：简单解释一下，就是在我们刚刚得到的trn_row中的每一行，根据真实的label，取对应的列，然后重新组合，得到真实的分值；
第三行代码：删除多余的num_labels+2维度。

至此，我们就成功取到了转移得分。

§ 第五部分
最后把多余的虚拟的start位置的得分给mask掉。这部分就不展开介绍了。

2.4.2.3 小结

全部讲完之后，还是定性的来理解一下转移得分，其实就是每个token上，我们不考虑这个token的词是谁，有什么特征，我们只关心它的上一个token的label是什么，以此来判断当前这个词的label，说白了，就像是“找规律”一样，类似于一种先验知识，我们通过学习一个transition矩阵，知道了某个label它的下一个label更有可能是谁，BERT-CRF模型，也正是因为在BERT编码器学到的特征之外，额外考虑了这部分“先验”的知识，才使得效果能够有所提升。

在发射分和转移分的计算上，最终都是落在了某个token的得分上，但是我们想要的，是整个序列整体的好坏，而不是某个位置的得失。对于这个问题，其实很简单，直接取平均就好。

回顾2.4.2中gold_score的计算，也正是在seq_len维度上取了平均。

拓展一下思维，除了取平均，我们当然也可以采用其他的思想来综合地衡量整个序列，例如，如果我们不怎么关心’O’label，更关心实体的话，可以根据label的类型不同，进行加权。

2.4.3 计算全部路径得分

这一部分一定要结合第1.3节来理解。

代码中的alpha，其实就是前面介绍的动态规划过程中为何的previous矩阵。

完整的代码如下：

    def calc_norm_score(self, logits, lens):
        """
        :param logits: (batch, seq_len, num_labels+2))
        :param lens: (batch)
        :return:
        """
        batch_size, _, _ = logits.size()
        alpha = logits.new_full((batch_size, self.label_size), -100.0)     # 生成一个(batch, num_labels+2)的-100
        alpha[:, self.start] = 0                                           # 每一步的状态分
        lens_ = lens.clone()

        logits_t = logits.transpose(1, 0)                                  # (seq_len, batch, num_labels+2)
        for logit in logits_t:
            # 对每一个step进行遍历
            logit_exp = logit.unsqueeze(-1).expand(batch_size,             # 新增了一个维度，并复制了num_labels+2份
                                                   self.label_size,
                                                   self.label_size)
            alpha_exp = alpha.unsqueeze(1).expand(batch_size,              # 同理, (batch, num_labels+2, num_labels+2)
                                                  self.label_size,
                                                  self.label_size)
            trans_exp = self.transition.unsqueeze(0).expand_as(alpha_exp)  # (batch, num_labels+2, num_labels+2)
            # 状态转移，每一步的得分是上一步的得分+状态分+转移分
            mat = logit_exp + alpha_exp + trans_exp                        # (batch, num_labels+2, num_labels+2)
            # 为下一步的转移生成prev矩阵
            alpha_nxt = log_sum_exp(mat, 2).squeeze(-1)                    # (batch, num_labels+2)

            mask = (lens_ > 0).float().unsqueeze(-1).expand_as(alpha)
            alpha = mask * alpha_nxt + (1 - mask) * alpha
            lens_ = lens_ - 1

        alpha = alpha + self.transition[self.end].unsqueeze(0).expand_as(alpha)   # 所有token遍历完之后加结束位
        norm = log_sum_exp(alpha, 1).squeeze(-1)

        return norm

然后我们一点一点来消化这部分代码：
首先前几行：

        batch_size, _, _ = logits.size()
        alpha = logits.new_full((batch_size, self.label_size), -100.0)     # 生成一个(batch, num_labels+2)的-100
        alpha[:, self.start] = 0                                           
        lens_ = lens.clone()

初始化了一个形状为(batch, num_labels+2)的alpha，如果不考虑batch的话，它其实就是1.3节里介绍的previous矩阵中的一行。

然后对logits进行了转置：

        logits_t = logits.transpose(1, 0)

交换了batch和seq_len这两个维度，因为我们的状态转移发生在一个time step到下一个time step之间，所以接下来要对seq_len这个维度进行循环，所以把它换到最前面。

然后开始遍历，计算每一个step的所有可能的路径的路径分之和：

        for logit in logits_t:
            # 对每一个step进行遍历
            logit_exp = logit.unsqueeze(-1).expand(batch_size,             # 新增了一个维度，并复制了num_labels+2份
                                                   self.label_size,
                                                   self.label_size)
            alpha_exp = alpha.unsqueeze(1).expand(batch_size,              # 同理, (batch, num_labels+2, num_labels+2)
                                                  self.label_size,
                                                  self.label_size)
            trans_exp = self.transition.unsqueeze(0).expand_as(alpha_exp)  # (batch, num_labels+2, num_labels+2)
            # 状态转移，每一步的得分是上一步的得分+状态分+转移分
            mat = logit_exp + alpha_exp + trans_exp                        # (batch, num_labels+2, num_labels+2)
            # 为下一步的转移生成prev矩阵
            alpha_nxt = log_sum_exp(mat, 2).squeeze(-1)                    # (batch, num_labels+2)

            mask = (lens_ > 0).float().unsqueeze(-1).expand_as(alpha)
            alpha = mask * alpha_nxt + (1 - mask) * alpha
            lens_ = lens_ - 1

可以看到，logit被复制了num_labels+2份（也就是$m$份），logits是什么呢，前边的代码介绍中说了，是特征提取模型的特征映射到num_labels这个空间下的“概率”，也就是发射得分。

然后alpha也被同样的复制，就得到了previous矩阵。

再然后，得到了转移矩阵。

三个矩阵具有相同的形状(batch, num_labels+2, num_labels+2)，对应位置元素三项相加，就是在执行状态转移了，得到的这个mat，就是1.3节对应的$Q$了，紧接着对它求logsumexp，就得到了当前step（也就是截止当前token长度）的所有路径的得分之和。

算完了当前的step，再把这个alpha_nxt更新到alpha，作为下一个step的previous矩阵。

在遍历的最后，我们还需要把seq_len维度上的padding的部分给mask掉（因为代码在实际操作的时候是批处理的，所以短的句子末尾的padding需要mask），这样一来，一次完整的遍历就结束了。

当整个for循环完成之后，就到达了序列的末尾，最后要注意一下边界条件，要把结束位再算一下，就大功告成啦。

至于logsumexp是怎么计算的，这一版代码的实现方法如下：

def log_sum_exp(tensor, dim=0, keepdim: bool = False):
    """LogSumExp operation used by CRF."""
    m, _ = tensor.max(dim, keepdim=keepdim)
    if keepdim:
        stable_vec = tensor - m
    else:
        stable_vec = tensor - m.unsqueeze(dim)
    return m + (stable_vec.exp().sum(dim, keepdim=keepdim)).log()

回顾优化目标：
$$Prob=\frac{e^{p_{real}}}{e^{p_1}+e^{p_2}+...+e^{seqlen\ast numlabels}}$$
2.4.2节中，我们介绍了目标变量的分子部分的计算，2.4.3节中，介绍了分母的计算，这样一来，就可以回到2.4.1节中，完成损失函数的计算了。

2.5 模型的训练

之前讲过了本文的重点是帮助大家理解CRF的运作，所以具体怎么使用，会比较简略的介绍。

在计算损失函数之后，接下来要关心的是，如何把CRF模型放进BERT-CRF这个框架中去，并实现对它的训练呢？

在2.3节中，已经介绍了，BERT的编码结果是怎样输入给CRF的，

假设已经实例化好了bert模型和crf模型：

import torch.nn as nn
from transformers import BertModel, BertTokenizer
bert = BertModel.from_pretrained('bert-base-uncased')
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
crf = CRF(vocab)

假设bert部分的损失采用的是交叉熵损失：

bert_criteria = nn.CrossEntropyLoss()

然后计算了bert的序列标注得分：

text = 'your text here.'
inputs = tokenizer(text)
bert_out = bert(inputs['input_ids'], attention_mask=inputs['attention_mask'])[0]

label_ffn = nn.Linear(bert_hidden_size, num_labels, bias=True)
label_scores = label_ffn(bert_out)
label_scores_softmax = label_scores.softmax(dim=2)

进而计算bert的损失：

label_scores_softmax = label_scores_softmax .view(-1, entity_type_num)  # 这里的entity_type_num是实体类型数
bert_loss = bert_criterira(label_scores_softmax, real_labels)  # real_labels是真实标签铺平

然后按照2.3节的步骤，把bert_out给到crf，计算crf的损失，并加到bert损失上（注意符号，求crf的损失要取负号）：

label_scores = crf.pad_logits(label_scores)
crf_loglik = crf.loglik(label_scores,
                        label_idxs,
                        token_nums)
total_loss = bert_loss - crf_loss.mean()

最后，把这部分内容写到整个BERT-CRF模型训练时的forward方法里就可以了。

2.6 viterbi解码

解码发生在模型的预测阶段。这一部分会讲的相对简略一点，因为涉及到的思想和代码在之前其实都已经出现过了。

当我们训练好了一个CRF模型，这个模型的转移矩阵transition已经确定下来了，接下来我们需要根据外部的输入$X$，也就是特征提取模型计算出来的logits，来结合CRF模型的状态转移，解码出最优的路径，作为序列标注任务的最终输出结果。

暴力解法当然是最容易想到的，不管序列有多长，全部的路径是有限的，那就把每一条路径的得分全都计算出来，然后取得分最高的。但是暴力法的复杂度，随着序列长度的增加，是呈指数增长的，因为在每一个token上，都会有$m$种label可以选择，这样的复杂度，在真实场景中显然是无法接受的。

因此，viterbi解码被引入了，它的本质其实还是动态规划。
我们用$Scor{e}_{[start][end]}$来表示从$start$到$end$位置的所有可能的得分，那么显然，求解的目标就是从开始位置$sos$到结束位置$eos$的所有可能的路径中，得分最大的一条路径：
$$Path(max(Scor{e}_{[sos][eos]}))$$
那么，就可以向前递推，当我们想要求eos位置的最大分数，其实就是求红色圈中的三者得分转移到eos位置中的得分最大者：

那么在step3时，每一项，同样是求前面一步中，三项转移到step3的得分的最大者。

下面是代码，如果不太理解的话可以结合前面求所有路径分的动态规划过程，回顾一下torch中这几个操作时在做什么。

    def viterbi_decode(self, logits, lens):
        """Borrowed from pytorch tutorial
        Arguments:
            logits: [batch_size, seq_len, n_labels] FloatTensor
            lens: [batch_size] LongTensor
        """
        batch_size, _, n_labels = logits.size()
        vit = logits.new_full((batch_size, self.label_size), -100.0)           # (batch, num_labels)形状的全-100
        vit[:, self.start] = 0                                                 # vit是动态规划中的状态转移，记录所有路径得分
        c_lens = lens.clone()

        logits_t = logits.transpose(1, 0)                                      # (seq_len, batch, num_labels)
        pointers = []                                                          # 记录每一个step的label中对应的上一步的最大分
        for logit in logits_t:
            # 仍然是在seq_len的维度上进行遍历
            vit_exp = vit.unsqueeze(1).expand(batch_size, n_labels, n_labels)  # (batch, num_labels, num_labels)
            trn_exp = self.transition.unsqueeze(0).expand_as(vit_exp)          # 相同形状的转移分
            vit_trn_sum = vit_exp + trn_exp
            vt_max, vt_argmax = vit_trn_sum.max(2)                             # 在from的维度上求最大

            vt_max = vt_max.squeeze(-1)                                        # 删除求最值时作废的维度
            vit_nxt = vt_max + logit                                           # 为下一个step做准备
            pointers.append(vt_argmax.squeeze(-1).unsqueeze(0))                # 当前step的所有label各自对应的上一step的最大分

            mask = (c_lens > 0).float().unsqueeze(-1).expand_as(vit_nxt)       # 每走一步，剩下的部分的有效mask就会少一个
            vit = mask * vit_nxt + (1 - mask) * vit

            mask = (c_lens == 1).float().unsqueeze(-1).expand_as(vit_nxt)
            vit += mask * self.transition[self.end].unsqueeze(                 # mask掉padding部分
                0).expand_as(vit_nxt)

            c_lens = c_lens - 1                                                # 对mask生效

        pointers = torch.cat(pointers)
        scores, idx = vit.max(1)                                               # 在to_label上求最大以找到得分最高的路径
        paths = [idx.unsqueeze(1)]                                             # 删除求最值时作废的维度
        for argmax in reversed(pointers):
            idx_exp = idx.unsqueeze(-1)
            idx = torch.gather(argmax, 1, idx_exp)
            idx = idx.squeeze(-1)

            paths.insert(0, idx.unsqueeze(1))

        paths = torch.cat(paths[1:], 1)
        scores = scores.squeeze(-1)

        return scores, paths

结束

本文从代码实现的角度，详细的介绍了CRF的运作原理，希望以此来帮助大家加深对CRF的理解和印象。创作不易，如果本文对你有所帮助的话，麻烦留下一个免费的赞。我们下期再见。