深度学习(十) Unsupervised Learning 理论部分

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

前面我们提到过很多个无监督学习方法，但是一直没有系统地介绍这些学习方法内容，这次将会从机器学习的角度去剖析它们。

一、无监督学习与监督学习的区别

1. 原理不同
   监督学习是指利用一组已知类别的样本调整分类器的参数，使其达到所要求性能的过程，所以监督学习需要给数据打标签。
   无监督学习指根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题的过程，无监督学习不需要给数据打标签。
2. 核心不同
   监督学习的核心是分类，有监督的工作是选择分类器和确定权值。
   无监督学习的核心是聚类（将数据集合分成由类似的对象组成的多个类），无监督的工作是密度估计（寻找描述数据统计值），这意味着无监督算法只要知道如何计算相似度就可以开始工作。
3. 定性过程不同
   监督学习的输出结果，也就是分好类的结果会被直接贴上标签，是好还是坏。也即分类分好了，标签也同时贴好了。
   无监督学习的结果只是一群一群的聚类，如果想要定性，还需要后续设计算法去进行定性。
4. 维度处理不同
   监督学习的输入如果是n维，特征即被认定为n维，通常不具有降维的能力。
   而无监督经常要参与深度学习，做特征提取，或者干脆采用层聚类或者项聚类，以减少数据特征的维度。
5. 可解释性不同
   监督学习一般不具有很强的可解释性，因为它的训练过程一般是黑盒子。
   无监督学习由于核心思想是聚类，知道聚类的原因与后续的定性处理，所以可解释性要强的多。

二、K-means

1.K-means的优缺点

1. 优点:

• 原理简单，实现方便，算法复杂度低，收敛速度快；
• 模型的可解释性较强；
• 调节参数的数量较少，主要需要调参的参数仅仅是簇数K；

2. 缺点:

• 采用迭代方法，聚类结果往往收敛于局部最优而得不到全局最优解
• 易受噪声、边缘点、孤立点影响；
• K 值需要人为设定，不同 K 值得到的结果不一样
• 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类

2.各种距离

想要了解K-means的计算原理，我们首先要理解一些基础概念跟距离模型。
首先我们设两个点 $x=(x_1,x_2...x_n),y=(y_1,y_2...y_n)$

1. 闵可夫斯基距离
   $$d(x,y)=(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$
   其中$p\ge 1$,事实上这个也是一个$L_p$范数
2. 欧氏距离
   欧氏距离是最常用的距离之一，其实是闵可夫斯基距离的特殊情况之一，是一个二范数，可以表征最短距离。
   $$d(x,y)=(\sum _{i=1}^n|x_i-y_i{|}^2{)}^{\frac{1}{2}}$$
3. 曼哈顿距离
   曼哈顿距离也是很常用的距离之一，也是闵可夫斯基距离的特殊情况之一，是一个一范数，可以表征垂直方向上(x和y方向)的距离之和
   $$d(x,y)=\sum _{i=1}^n|x_i-y_i|$$
   
   图中绿色边是欧氏距离，其他都是曼哈顿距离

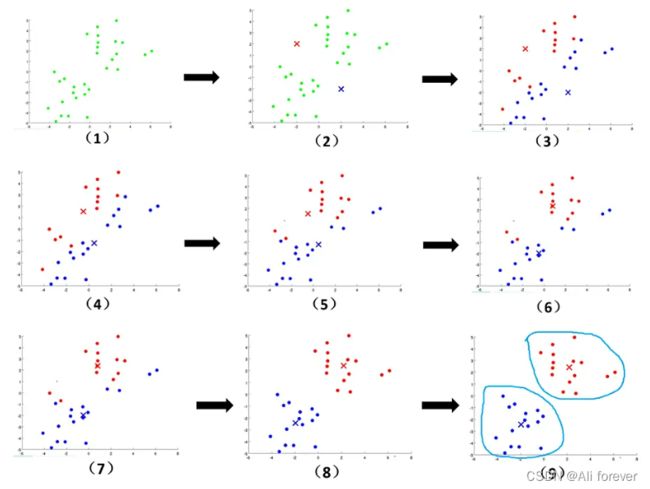
3.K-means算法

簇：所有数据点的点集合，簇中的对象是相似的
质心：簇中所有点的中心（由簇中所有点的均值求得）

1. 随机初始化k个点作为簇质心
2. 然后将样本集中的每个点分配到一个簇中；计算每个点与质心之间的距离（常用欧式距离和余弦距离），并将其分配给距离最近的质心所对应的簇中；
3. 更新簇的质心。每个簇的质心更新为该簇所有点的平均值；
4. 反复迭代2 - 3 步骤，直到达到某个终止条件；

聚类效果的评价指标一般为SSE(平方误差和)，SSE越小越说明质点越来越接近簇心，聚类效果越好。
$$SSE=\sum _{i=1}^k\sum _{x\in C}(x-{\mu }_i{)}^2$$

三、HAC(层次汇合聚类)

1.HAC的优缺点

1. 优点

• 距离的定义比较容易，而且比较自由
• 可以生成非球形的簇，发现层次间的关系。
• 有时可以不用指定所需类别个数，可以通过阈值来进行类的划分

2. 缺点

• 在建树过程中要计算每个样本间的距离，计算复杂度较高；
• 容易受异常点的影响
• 容易形成链状的簇

2.HAC的算法过程

1. 把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；
2. 寻找各个类之间最近的两个类，把他们归为一类（这样类的总数就少了一个）；
3. 重新计算新生成的这个类与各个旧类之间的相似度；
4. 重复2和3直到所有样本点都归为一类，就结束了

这样下来，你会发现通过这个手段，HAC生成了一颗自底向上的树，并且终止条件可以是一个阈值，比较两个类的距离，如果大于某个阈值就可以停止进行聚类。
最后只需要在每一层上切一刀，相邻地叶子结点就是一个聚类。

四、PCA算法(主成分分析)

上面介绍的K-means与HAC都是聚类的方法，他们致力于将类别划分在一起，如何划分在一起，接下来将会介绍一些降维的方法。

1.为什么要使用PCA算法？

1. 聚类的缺点是以偏概全，强迫每个数据都要归顺于某一个簇，但是事实上一个数据可能归顺于多个簇，包含多个特征，如果这样做将会丢失掉这个数据得到其他特征，所以应该找一个向量去包含这些特征。
2. 许多变量之间存在相关性，如果对每个指标进行分析，将会是孤立的，无法利用到数据中心的很多信息，所以我们要在减少需要分析的指标同时，尽量减少原指标包含信息的损失

2.PCA算法的优缺点

1. 优点:

• 各主成分之间正交，可消除原始数据成分间的相互影响
• 用PCA技术可以对数据进行降维，同时对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息
• PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关
• 计算方法简单，主要运算是特征值分解，易于实现。

2. 缺点:

• 主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
• 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
• PCA是无监督的，不知道数据的标签，这样在降维映射之后可能会把两类数据混到一起。
• PCA是线性的，把一个三维空间中的S形分布的数据做PCA之后的效果，就是把S形拍扁，而非展开。
  

3.奇异阵分解(SVD)

1.奇异阵分解的作用以及应用

奇异阵分解的核心目标就是在低维空间中寻找最接近原矩阵A的低维矩阵M ,实现数据降维。
因为在数学上来说，一定能找到一个更低规模的矩阵去迫近原来高维度的矩阵，这样就实现了数据的压缩，提高后续处理的速度。
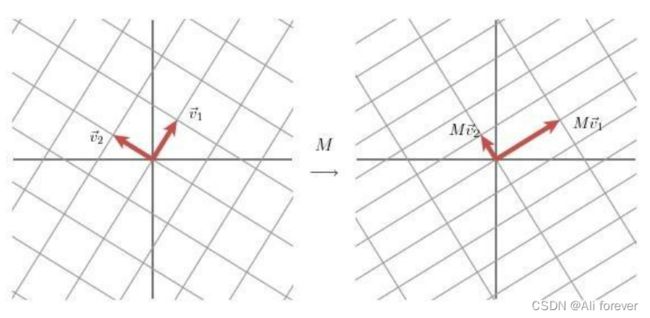
而奇异值分解的几何含义为：对于任何的一个矩阵，我们要找到一组两两正交单位向量序列，使得矩阵作用在此向量序列上后得到新的向量序列保持两两正交。
奇异阵分解的主要应用:

• 图像压缩
• 图像恢复
• 获取特征脸
• 谱聚类
• 从视频中删除背景

2.奇异阵分解原理

给定一个大小为M*N的矩阵A,我们可以将其分解成:
$$A_{m\ast n}=U_{m\ast m}{\Lambda }_{m\ast n}{V}_{n\ast n}$$
我们可以看到 U 跟 V两个矩阵都是方阵，而中间的特征矩阵则是一个非方阵，接下来我们将对我们的A矩阵进行对角化分解
$$A{A}^T=P{\Lambda }_1{P}^T$$
$$A^{T}A=Q{\Lambda }_2{Q}^T$$
由于对角化分解后的结果是一个方阵，所以这时我们的${\Lambda }_1,{\Lambda }_2$则分别是一个$m\ast m$和$n\ast n$的方阵，而P的大小也是$m\ast m$,Q的大小为$n\ast n$。
对角化分解后的两个矩阵$A{A}^T,A^{T}A$之间存在很大的关系，我们会发现虽然它们的特征矩阵不同，但是它们在对角线上的特征值是完全相等的，接下来我们只要取特征矩阵较小的那个那个特征矩阵作为我们的$\Lambda$就可以进行迫近了，因为这个特征矩阵已经包含了整个奇异阵分解的大部分有用信息，最后得出的分解结果为:(假设特征矩阵的秩为k)
$$A_{m\ast n}=U_{m\ast k}{\Lambda }_{k\ast k}{V}_{k\ast n}$$
注意:这里的特征值是求平方根后的结果，必须要保证最后的结果是正的
我们同时展开奇异阵分解，会得到如下式子:
$$A={\lambda }_1{u}_1{v}_1+{\lambda }_2{u}_2{v}_2+...{\lambda }_n{u}_n{v}_n$$
我们要做的就是将它们截断，截留前k个奇异值，得到新的迫近矩阵
$$M={\lambda }_1{u}_1{v}_1+{\lambda }_2{u}_2{v}_2+...{\lambda }_k{u}_k{v}_k$$

4.一维PCA的简单推导过程

PCA的目标是找到一组新的正交基 （从n维下降到k维），使得数据点在该正交基构成的平面上投影后，数据间的距离最大，即数据间的方差最大，这样数据就会越分散，越能区分开它们。如果数据在每个正交基上投影后的方差最大，那么同样满足在正交基所构成的平面上投影距离最大。

1. 设正交基$u_j$,数据点$x_i$在它上投影距离为$x_i^T{u}_j$，则所有数据在这个正交基中投影所得到的方差为:$$J_j=\frac{1}{m}\sum _{i=1}^m(x_i^T{u}_j-x_{center}^T{u}_j{)}^2$$
   其中m是样本数量，数据运算之前先对数据x进行0均值化，也叫去中心化，令$x_{center}=0$
   接下来我们将式子展开，得到$$J_j=\frac{1}{m}\sum _{i=1}^m(x_i^T{u}_j{)}^2=u_j^T(\frac{1}{m}\sum _{i=1}^m{x}_i^T{x}_i)u_j$$
   这个形式似曾相识，十分地与我们上面奇异阵分解的形式不约而同的相等，当我们将中间那串东西看作奇异阵分解中的特征矩阵即可化简成下面这种形式:
   $$J_j=u_j^{T}S{u}_j$$
   其中$S=\frac{1}{m}{\sum }_{i=1}^m{x}_i^T{x}_i$

2. 然后我们加入限制条件，也就是加上拉普拉斯算子进行限制:$$st:u_j^T{u}_j=1$$
   构造函数得到$$F(u_j)=u_j^{T}S{u}_j+\lambda (1-u_j^T{u}_j)$$
   通过梯度下降的方式求解这个函数的极值，得到的结果是:
   $$S{u}_j=\lambda u_j$$
   代回原式子，我们可以得到结果是
   $$J_{jmax}=u_j^T{\lambda }_j{u}_j={\lambda }_j$$

3. 然后统计所以基底$u=u_1,u_2..u_j$下的最大方差，可以得到:
   $$J_{max}=\sum _{j=1}^k{\lambda }_j$$
   这里的j是按照特征值大小来进行排序的吗，所以投影正交基为S的特征向量中的前k个最大特征值对应的特征向量。

4. 根据奇异阵分解，我们知道新的正交基$u\in svd(S)$,S即为X的协方差矩阵(同时是一个对角矩阵，因为$x_{center}=0$)。

5. 按照特征值从大到小排序，要降低为k维，那么取前k个特征值对应的特征向量，就是新的k个坐标轴

6. 最后将X映射到新的基底当中，完成我们的降维操作

5.更高维度的PCA投影

如果想要投影到更高维度，那么我们必须要设定多个维度的变换

这样随之而来的问题是会出现多个限制条件和多个方差函数，并且会出第一大特征和第二大特征，就会有多个特征向量值

五、manifold learning(流行学习)

1.为什么要使用流行学习？

1. 前面我们说过，PCA的降维是一种线性的降维方法，他把多维空间进行了压平，而不是展开，这样在计算欧氏距离就会产生问题，而流行模型在局部具有欧式空间的性质，可以利用这个性质进行降维映射，并且可以实现可视化。
2. 我们所能观察到的数据其实是由一个低维流形映射到高维空间上的（一个立方体可以展开为平面）。由于数据内部特征的限制，一些高维中的数据会产生维度上的冗余，实际上只需要比较低的维度就能唯一的表示。

2.多维标度分析(MDS)

1.为什么要使用MDS算法？

PCA的思想，它是找到一个最佳的投影方向使得数据在该方向投影之后保留足够多的信息。但这样只考虑了数据整体的分布情况（即方差），而没有考虑点与点之间的距离关系。但是我们希望降维前后能够保持距离关系不变，从而能够很好地进行可视化，而MDS算法能将距离固定为欧氏距离，保持彼此之间的相对距离变化最小，使其尽可能与原先的相似性大致匹配。

2.MDS算法步骤

1. 现在考虑将原始数据矩阵$X\in R^{d\ast m}$降维成$Z\in R^{d^{\prime }\ast m}$，其中 m 是样本点的个数。原始数据的维数是 d，希望将其降到 d’。那么我们要做的是找到这样的 m 个 d’ 维的向量
   $$mi{n}_z\sum _{i,j}(||z_i-z_j||-d_{ij}{)}^2$$
   其中$d_{ij}$是原始样本 i 和原始样本 j 之间的距离，
2. 我们对这个最小值展开，我们将得到:
   $$\begin{array}{rl}{d}_{ij}^2& =||z_i-z_j|{|}^2=||z_i|{|}^2+||z_j|{|}^2-2||z_i|{|}^T||z_j||\\ & =b_{ii}+b_{jj}-2b_{ij}\end{array}$$
3. 然后进行求和得到:
   $$\begin{array}{rl}\sum _{i=1}^m{d}_{ij}^2& =\sum _{i=1}^m{b}_{ii}+\sum _{i=1}^m{b}_{jj}-\sum _{i=1}^{m}2b_{ij}\\ & =tr(B)+m{b}_{jj}+0(中心化约束)\end{array}$$
4. 再对j求和得到结果是$2mtr(B)$
5. 根据上面的几个式子我们可以分别推导出$b_{ii},b_{jj},b_{ij}$的值，它们分别是
   
6. 接下来我们可以对B进行奇异阵分解了,实现降维。
   $$B=Z{Z}^T=U\Lambda U^T=({\Lambda }^{\frac{1}{2}}{U}^T{)}^T({\Lambda }^{\frac{1}{2}}{U}^T)$$
7. 截断后得到MDS的解$$Z={\Lambda }_{d’}^{\frac{1}{2}}{U}_{d’}^T$$

3.ISOMAP算法

ISOMAP是一种特殊的MDS算法，只是在距离阵的计算方法中不一样，其他都是一样的

1. 根据给定的欧氏距离阵，利用前面提到的最短路径算法得到调整的距离阵；
2. 将调整的距离阵代入MDS算法框架中。

Isomap算法是全局的，它要找到所有样本全局的最优解，当数据量很大时或者样本维度很高时，计算量非常大。

4.LLE算法(局部线性嵌入)

LLE算法主要就是为了解决ISOMAP算法全局最优的问题，实现局部最优

• LLE算法的简单步骤:
  step 1：确定近邻点,运用k近邻算法得到每个数据 $x_i$ 的 k 近邻点
  step 2: 求解权重系数矩阵
  
  step 3: 映射到低维空间,利用上面计算出来的最优解$w_{ij}$对低维空间进行映射
  
• LLE算法的优点:
  1）可以学习任意维的局部线性的低维流形。
  2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。
  3）可以处理非线性的数据，能进行非线性降维。
• LLE算法的缺点:
  1）算法所学习的流形只能是不闭合的，且样本集是稠密的。
  2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

3.t-SNE

1.t-SNE的优缺点

1. 优点:

• 如果用 PCA 降维进行可视化，会出现所谓的“拥挤现象”,而t-SNE就可以解决拥挤现象
  
• t-SNE 更加注重保留原始数据的局部特征

2. 缺点:

• 只能可视化，不用于数据转换，这是因为中间并没有出现任何的结构型网络，只是简单地对原数据集进行迫近，当有新的数据输入进来时，将会重新进行训练。
• 过于高维一般不直接使用，因为维数过高时，将会使变换矩阵十分地庞大，计算量过大。

2.t-SNE的过程

与前面MDS的思想一致，在变换前后两个点之间的相对距离应该保持一致，也就是原先距离近的数据，降维之后距离应该也很近；原先距离远的数据，降维之后距离应该也很远。
但是t-SNE的思想是将距离的远近看作概率分布，即变换前后都生成一个概率分布，通过KL散度来衡量它们的接近情况

1. 对于高维度中每一个数据点i，其概率分布为:
   $$p(j|i)=\frac{S(x_i,x_j)}{{\sum }_{k\ne i}S(x_i,x_j)}$$
   其中S表征的是两个点i和j之间的相似度
2. 对于低维度中每一个数据点i，其概率分布为:
   $$q(j|i)=\frac{S^{\prime }(z_i,z_j)}{{\sum }_{k\ne i}{S}^{\prime }(z_i,z_j)}$$
   其中S’表征的是两个点i和j之间的相似度,S跟S’可以是两个不一样的表征函数
3. 接下来引入KL散度来进行衡量两个分布的相似性:
   $$L(z_1,z_2...z_n)=\sum _{i=1}^n\sum _{j\ne i}p(j|i)\log \frac{p(j|i)}{q(j|i)}$$
4. 用梯度下降算法求得令损失函数最小的那一组z，必要时可以加入动量来加速我们的收敛。

3.t-SNE的相似函数

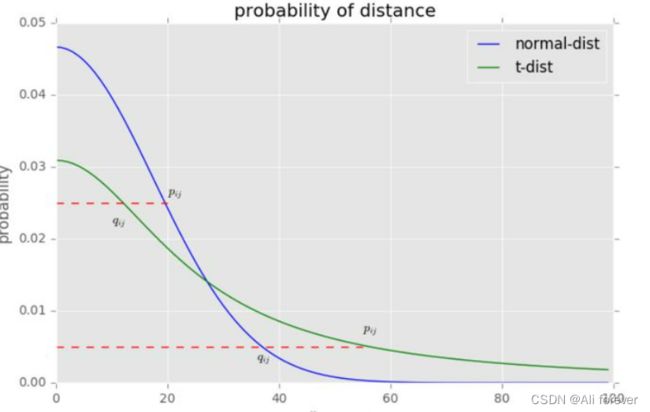
在SNE中我们采用的是指数分布，因为指数分布的收敛快，只要距离一拉开，那么相似度迅速减小，从而在低维空间中将那些稍有间隔的点拉得很开。
$$S(x_i,x_j)=exp(\frac{-||x_i-x_j|{|}_2^2}{(2\sigma {)}^2})$$
但在t-SNE中我们采用的就是t分布，t分布能够更好地解决拥塞问题，距离接近的点变得更近；距离较远的点变得更远。
$$S^{\prime }(x_i,x_j)=\frac{1}{(1+||x_i-x_j|{|}_2^2)}$$

总结

本文介绍了Unsupervised Learning非监督学习，并且最后附上本文章的思维导图，希望能帮助大家快速地熟悉Unsupervised Learning的运作规律。