论文研读——n个物体相互间的碰撞避免
论文研读——Reciprocaln-body Collision Avoidance
此篇文章为论文的学习笔记,只供学习使用,不作商业用途,侵权删除。并且本人学术功底有限,如有思路不正确的地方欢迎批评指正!
摘要
在本文中,我们提出了一种形式化的n个物体相互避碰方法,其中多个移动机器人在一个共同的工作空间中移动时需要避免彼此碰撞。在我们的公式中,每个机器人完全独立行动,不与其他机器人通信。在速度障碍定义的基础上,通过将问题简化为求解一个低维线性规划,得到了无碰撞运动的充分条件。我们在几个密集而复杂的模拟场景中测试了我们的方法,其中包括数千个机器人,并在短短几毫秒内计算出所有机器人的无碰撞动作。据我们所知,该方法是第一个能够保证大量机器人在杂波工作空间中的局部无碰撞运动的方法。
1、介绍
碰撞避免是机器人的一个基本问题。这个问题通常可以定义为一个自主移动机器人在有障碍物和/或其他移动实体的环境中导航,机器人使用一个连续的感知和行动循环。在每个循环中,机器人的一个动作必须根据对环境的局部观察来计算,这样机器人在朝着目标前进时就不会与障碍物和其他移动机器人发生碰撞。
在本文中,我们提出了一种快速和新颖的方法,可以同时确定许多(可能是数千)机器人的行动,每个机器人可能有不同的目标。每个机器人的动作都是独立计算的,没有机器人之间的通信或中心协调。然而,我们证明了我们的方法保证了每个机器人的无碰撞运动。
我们使用一个简化的机器人模型,其中每个机器人都假定有一个简单的形状(圆形或凸多边形)在二维工作空间中移动。此外,我们假设机器人是完整的,即它可以向任何方向移动,这样每个机器人的控制输入简单地由一个二维速度向量给出。此外,我们假设每个机器人都有完美的感知能力,能够推断出环境中障碍物和其他机器人的确切形状、位置和速度。
主要结果:我们提出了一个严格的方法来处理往复体碰撞避免,为每个机器人提供一个有效的无碰撞条件未来至少有固定数量的时间,仅限于使用其他机器人相同的避碰协议。我们的方法基于可靠性。这意味着每个机器人都会考虑其他机器人的观测速度,以便避免与它们发生碰撞,也避免机器人从中选择自己的速度它的速度空间,其中某些区域被标记为“禁止”,因为其他机器人的存在。我们的公式“最佳交互碰撞避免”,为每个机器人推断出一个速度为允许选择,以确保避免碰撞。那么机器人呢从所有允许的半平面的交点中选择其最佳速度可以使用线性规划有效地完成。在一定条件下在机器人密集的情况下,由此产生的线性规划可能是不可行的,在这种情况下我们使用三维线性规划选择“最安全”的速度。
我们在几个包含数千个机器人的复杂模拟场景中试验了我们的方法。由于每个机器人都是独立的,我们可以完全并行计算每个机器人的动作,并报告非常快的实时运行时间。此外,我们的实验表明,我们的方法实现了令人信服的运动,平滑和无碰撞。
本文的其余部分组织如下。我们从第2节中讨论以前的工作开始。在第3节中,我们正式定义了本文中要解决的问题。在第4节中,我们推导了一个机器人相对于另一个机器人的最佳互反避碰的允许速度半平面,并在第5节中展示了如何使用这种方法在多个机器人之间导航。我们在第6节报告实验结果,在第7节总结。
2、之前的工作
避碰问题已经得到了广泛的研究。许多方法假设观察到的障碍物是静态的(即不移动的),并计算机器人的立即行动,以避免与障碍物发生碰撞,在许多情况下考虑机器人的运动学和动力学。如果障碍也在移动,这种方法通常会根据对障碍位置的新解读反复“重新规划”。如果障碍物的移动速度比机器人慢,这种方法就很有效,但在快速障碍物(如穿越公路)中,需要特别考虑障碍物的速度。这个问题通常被称为“小行星躲避”,通常通过推算观测到的速度来估计障碍物未来的位置。
当障碍物不仅仅是在不考虑其环境的情况下移动,而且也是试图避免碰撞的智能决策实体时,避免碰撞的问题就变得更加困难了。简单地将它们视为移动的障碍物可能会导致振荡,如果其他实体也将所有其他机器人视为移动的障碍物。因此,必须特别考虑到其他实体的反应性质,以确保避免碰撞。然而,机器人可能无法与其他实体交流,也可能不知道它们的意图。我们称这个问题为互反避碰,这是本文的重点。
速度障碍(VO)是一种成功的基于速度的方法来避免与移动障碍物的碰撞;它们为机器人选择速度以避免与以已知速度移动的障碍物发生碰撞提供了充分和必要的条件。根据速度互反障碍(RVO)的定义,将该方法推广到机器人-机器人避碰中,其中两个机器人都假设选择另一个机器人诱导的速度外的速度。然而,这个公式只保证在特定条件下避免碰撞。事实上,两个机器人在彼此的RVO内选择一个速度是导致碰撞的充分条件,但反之则不成立。在速度障碍定义的基础上,提出了最优互反避碰原则,为多机器人之间避免碰撞提供了充分条件。
我们注意到,通过在所有机器人速度的二维空间中定义复合速度障碍,可以为多个(说)机器人选择避碰速度提供一个充分必要条件。然而,这不仅在计算上不切实际,而且还需要机器人之间的中心协调。这与本文所关注的分布式多机器人导航类型是不相容的,即每个机器人在自己的二维速度空间中独立地同时选择自己的速度。
3、问题定义
本文所讨论的问题的形式化定义如下。让一组n个机器人共享一个环境。为了简单起见,我们假设机器人是圆盘形的,并且在平面R2中移动(我们在本文中提出的定义和算法可以很容易地扩展到翻译多边形,也可以扩展到更高维度)。每个机器人A都有一个当前位置pA(圆盘的中心),一个当前速度VA和一个半径rA。这些参数是机器人外部状态的一部分,即我们假设其他机器人可以观察到这些参数。此外,每个机器人都有一个最大速度 v A m a x v^{max}_A vAmax和一个首选速度 v A p r e f v^{pref}_A vApref,这是机器人在没有其他机器人挡路时所假定的速度(例如,一个指向机器人目标的速度,其大小等于机器人的首选速度)。我们认为这些参数是机器人内部状态的一部分,因此不能被其他机器人观察到。
任务是每个机器人独立地(同时地)为自己选择一个新的速度 V A n e w V^{new}_A VAnew,这样所有的机器人都能保证在预设的时间 τ \tau τ 内不受碰撞,当他们继续以新的速度移动时。作为一个次要目标,机器人应该选择他们的新速度尽可能接近他们的首选速度。机器人之间不允许相互交流,只能使用对对方机器人当前位置和速度的观察。然而,每个机器人都可以假设其他机器人使用与自己相同的策略来选择新的速度。
我们将这个问题命名为“往复体避碰”。注意,这个问题不能用中心协调来解决,因为每个机器人的首选速度只有机器人自己知道。在第4节中,我们给出了每个机器人选择一个(至少) τ \tau τ 时间内无碰撞速度的充分条件。在第5节中,我们将展示如何在多机器人导航的连续循环中使用这一原则。
4、相互的碰撞避免
4.1 准备工作
对于两个机器人A和 B,速度障碍 V O A ∣ B τ VO^\tau_{A|B} VOA∣Bτ(对于速度障碍A 由 B 推导出的时间窗口 τ \tau τ )是A相对于B的所有相对速度的集合,这会导致A和B在时间 τ \tau τ之前的某个时刻发生碰撞。它的正式定义如下:D (p,r)表示一个以半径为r的开口圆盘中心P:
![]()
此时:
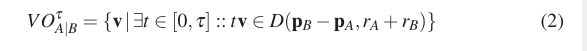
速度障碍的几何解释如图1所示。注意, V O A ∣ B τ VO^\tau_{A|B} VOA∣Bτ和 V O B ∣ A τ VO^\tau_{B|A} VOB∣Aτ在原点是对称的。
4.2 最优相互撞碰避免
定义1(最佳互反避免碰撞)。以及相关的公式定义。
5、 n个物体的碰撞避免
在本节中,我们将展示如何应用上面定义的ORCA原则在多个移动机器人之间执行身体碰撞避免,并讨论如何在这个框架中合并静态障碍。
5.1 基本方法
总体方法如下。每个机器人执行一个连续的感知和动作周期,时间步长∆t。在每次迭代中,机器人获取其他机器人(以及自身)的半径、当前位置和当前的优化速度。基于这一信息,机器人推断出相对于机器人B的速度或 O R C A A ∣ B τ ORCA^\tau_{A|B} ORCAA∣Bτ的允许半平面。对于所有机器人来说,允许的速度集合是由彼此机器人诱导的允许速度半平面的交点,我们表示这个集合 O R C A A τ ORCA^\tau_A ORCAAτ如下公式:

注意,这个定义还包括robotA的最大速度限制。
接下来,机器人自己选择一个新的速度 v A n e w v^{new}_A vAnew,在所有允许速度范围内的速度中最接近它的首选速度 v A p r e f v^{pref}_A vApref:
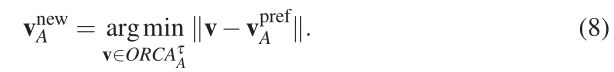
下面我们将展示如何有效地计算这个速度。最后,机器人到达了它的新位置;

感知-作用循环往复。
5.2选择最优的速度
我们还没有解决的一个问题是如何为每个机器人选择 v A o p t v^{opt}_A vAopt。为了让机器人在没有通信的情况下推断出半平面, v A o p t v^{opt}_A vAopt必须对其他机器人可见。后面我们讨论一些合理的可能性。
5.3 密集的条件
如果我们选择 v A o p t = v A v^{opt}_A = v_A vAopt=vA,那么在机器人密度非常高的情况下,可能不会有一个单一的速度满足线性规划的所有约束。换句话说,集合 O R C A A τ ORCA^\tau_A ORCAAτ是空的,第5.1节的算法返回线性规划是不可行的。在这种情况下,不能保证选择一个无碰撞速度。相反,我们为机器人选择“可能最安全”的速度,即最低限度地“穿透”其他机器人所引起的限制的速度。更正式地说,让 d A ∣ B ( v ) d_{A|B}(v) dA∣B(v)表示速度vto半平面边缘的有符号(欧几里得)距离或 O R C A A τ ORCA^\tau_A ORCAAτ。如果 v ∈ O R C A A ∣ B τ v∈ORCA^\tau_{A|B} v∈ORCAA∣Bτ,则 d A ∣ B ( v ) d_{A|B}(v) dA∣B(v)为负。现在我们选择速度,使其他机器人到任何半平面的最大距离最小化:
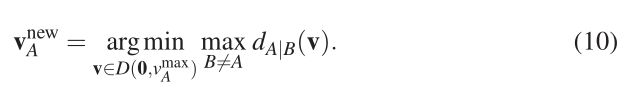
几何上,这可以解释为以相等的速度垂直向外移动半平面 O R C A A ∣ B τ ORCA^\tau_{A|B} ORCAA∣Bτ的边缘,直到有一个速度有效。
5.4 静态障碍
到目前为止,我们只讨论了机器人如何避免彼此碰撞,但典型的多机器人环境也包含(静态)障碍。我们可以很容易地将它们纳入上述框架。我们基本上遵循上述相同的方法,但关键的不同是,障碍物不会移动,所以机器人应该完全负责避免与它们碰撞。
我们通常可以假设障碍物是一组线段的集合。让O成为这样的线段之一,让a是一个半径 r A r_A rA,位置在 p A p_A pA的机器人。由障碍物引起的的速度障碍 V O A ∣ O τ VO^\tau_{A|O} VOA∣Oτ,定义如下:
![]()
在有障碍物的情况下,我们为所有的机器人A选择 A A o p t = 0 A^{opt}_A=0 AAopt=0。这就保证了机器人总是存在一个有效的速度,以避免在τ时间内与障碍物发生碰撞。相对于其他机器人,我们通常可以使用较小的τ值,因为如果需要避开其他机器人,机器人通常不应该“害羞”地朝障碍移动。另一方面,机器人相对于障碍物的允许速度的限制应该是困难的,因为应该不惜一切代价避免与障碍物的碰撞。因此,当第5.1节的线性规划由于机器人密度过高而不可行的时候,障碍物的约束并没有放松。
我们注意到,上面定义的允许速度的半平面只确保机器人避免与障碍物碰撞;它们不会让机器人在它们周围移动。机器人围绕障碍物向目标运动的方向应该反映在机器人的优先速度上,该速度可以通过(有效的)全局路径规划技术得到。
6、实验结果
为了测试我们的技术,我们运行了几个模拟。我们执行了小规模模拟来测试局部行为,并执行了大规模模拟来分析性能扩展。
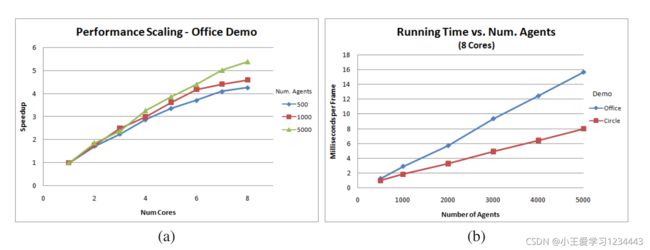
模拟1000个探员试图通过圆心移动到对跖点位置。机器人能顺利地穿过中心形成的拥堵如下图所示:

1000名虚拟特工疏散办公室的模拟截图,这是人群模拟的一部分,如下图所示:

性能图:(a) 1 - 8核疏散模拟的性能扩展。(b)不同数量的agent在8核上的运行时间(越低越好)。两种模拟都随着代理的数量近似线性地扩展。
结论与未来工作
在本文中,我们提出了一种有效的方法,为多个机器人提供了一个充分的条件来选择一个动作,以避免与其他机器人的碰撞,尽管每个动作都是独立的,不与其他机器人通信。在我们的实验中,我们的往复体避免碰撞的方法表现出快速的运行时间和平滑、令人信服的行为。
我们使用了一个简单的机器人模型,其中忽略了运动学和动力学。对未来工作的一个重要扩展是考虑到这些限制。我们可以将此作为一个后处理步骤,在此过程中,计算出的新速度将被“固定”到运动学和动态约束所允许的范围内。这将不再严格保证避免碰撞,但它可能在实践中工作得很好。一个更彻底的解决方案是,在推导机器人的允许速度时,从本质上考虑这些因素。
在本文中,我们只演示了二维环境下的结果。然而,所有的定义和算法都可以扩展到三维。这可能是有趣的应用,如自动飞行器,或成群的鸟或鱼的模拟。未来工作的另一个重要方向是在真实机器人上实现所提出的框架,并纳入传感不确定性。我们相信,在该实施中,我们可以相对容易地用ORCA方案取代RVO方案。