论文研读笔记(一)——多智能体强化学习的相对分布编队和避障
Relative Distributed Formation and Obstacle Avoidance with Multi-Agent Reinforcement Learning(多智能体强化学习的相对分布编队和避障)
最近我在学习多机器人编队导航的论文,此篇文章为“[1] Yan Y , Li X , Qiu X , et al. Relative Distributed Formation and Obstacle Avoidance with Multi-agent Reinforcement Learning[J]. arXiv e-prints, 2021.”的论文学习笔记,只供学习使用,不作商业用途,侵权删除。并且本人学术功底有限,如果有思路不正确的地方欢迎批评指正!
论文所提及算法的代码如下:https://github.com/efc-robot/MultiVehicleEnv
摘要
多智能体编队以及避障是多智能体系统领域研究最活跃的课题之一。尽管模型预测控制 (MPC) 和模糊控制等一些经典控制器取得了一定程度的成功,但它们中的大多数都需要在恶劣环境中无法获得的精确全局信息。另一方面,一些基于强化学习(RL)的方法采用领导者-跟随者结构来组织不同智能体的行为,这牺牲了智能体之间的协作,从而在可操作性和鲁棒性方面遇到瓶颈。在本文中,文中提出了一种基于多智能体强化学习(MARL)的分布式编队和避障方法。文中系统中的智能体仅利用本地和相关信息来做出决策并分布式控制自己。多智能体系统中的智能体在其中任何一个断开连接的情况下,会迅速将自己重新组织成一个新的拓扑结构。与基线(经典控制方法和另一种基于 RL 的方法)相比,文中的方法在编队误差、编队收敛速度和避障成功率方面取得了更好的性能。通过阿克曼转向车辆的仿真和硬件实现验证了文中方法的可行性。
- 个人总结:提出了一种基于MARL的分布式编队和避障的方法,智能体通过本地及相关信息自我决策,且能够在断开连接的情况下迅速组成新的拓扑,从而实现了编队误差、编队收敛速度和避障成功率上的更好性能
摘要
避免障碍的同时控制是多智能体系统(MAS)的最基本功能之一。在诸如车辆互联网之类的场景中,自动排列(作为一项编队任务)和超车(作为避免障碍的任务)是最常见和最重要的动作。大多数先前的研究[1]-[6] 将整个任务视为优化问题,以根据目的地和奖励功能计划智能体的路线和运动,同时在避免运动过程中避免障碍物和其他智能体等约束。由于优化问题倾向于非凸,因此提出了一些基于经典层次控制(例如模型预测控制(MPC)[7],[8]或模糊控制[9]来处理该问题。但是,他们中的大多数都需要高精度的全球信息,例如GPS和数字地图,从而在紧急灾难中的搜索和撤退等严酷的环境中产生不适用性。此外,在这些传统方法中,智能体之间的协作并未完全考虑,这意味着在多智能体协作方面仍然有很大的改进空间。在过去的几十年中,由于强化学习(RL)和控制理论[10]-[13]的深刻组合,智能试剂的成熟度得到了很大的增强。以前的一些文献[14],[15]进行RL以实现自动形成控制和避免障碍,但是他们中的大多数人都无法摆脱领导者的结构,主要专注于控制某个单一智能体[16]-[20]。如果领导者被破坏或断开连接,则整个系统将崩溃。仅通过数值模拟来验证常见的基于RL的作品。很少有作品在硬件平台上实现其算法,但仅考虑全向轮模型[21],[22],这不足以用于实用的阿克曼转向[23]车辆系统。
在本文中,文中使用多智能体近端策略优化 (MAPPO) [24]、[25] 设计了一种分布式编队和避障算法。所提出的方法只需要实际系统容易获得的相关信息,并且控制策略可以分布式执行。文中工作的贡献如下:1)分布式。文中提出了一种独立于全球位置信息的相对编队策略。智能体通过考虑时空合作获得的网络拓扑而不是绝对坐标或方向角度信息来调整他们的位姿。文中避免了leader-follower结构,训练了一个支持去中心化执行的策略,更健壮;2)自适应。通过政策提炼将多种形成策略整合到文中的模型中。如果编队中的任何智能体被破坏或断开连接,其他智能体将自适应地重新组织成一个新的拓扑以继续他们的工作。此外,文中使用课程学习 [26] 来加速避障训练,提高 MAS 在复杂环境中的稳定性。 3) 有效。文中通过数值模拟将文中的方法与现有的传统控制算法(MPC[7]、模糊控制[9])和基于 RL 的领导者-跟随者方法[19]进行了比较。平均编队误差、编队收敛率和避障成功率的结果表明,文中的方法比基线方法取得了更好的性能。 4)实用。文中使用具有阿克曼转向几何的智能汽车作为智能体在硬件平台上执行文中的方法。
- 个人总结:工作贡献:1、分布式,通过网络拓扑调整智能体的位姿,以去中心化;2、自适应,当编队出现意外,能迅速的中心组成一个新的网络;3、有效性,平均编队误差、编队收敛率和避障成功率有更好的性能;4、实用性,可以在硬件上执行该方法。
问题表述
1.相对定位和编队误差
高精度的位置信息是编队、避障等复杂任务的前提和重要保障。最先进的研究主要集中在全局定位优化上,这是在恶劣环境中成本高且无保障的[27]。在车联网等场景中,人们更关注反映网络几何形状的相对关系[28],因为相对拓扑足以完成超车或编队等机动,并且更容易获得。
考虑由 N 个代理组成的二维结构,代理的集合表示为 N。代理 i 的全局位置表示为 p i = [ x i , y i ] T pi = [x_i,y_i]^T pi=[xi,yi]T。在智能体 i i i的局部坐标系中,任何其他智能体 j 的相对位置表示为 p i ← j = [ x j − x i , y j − y i ] T p_{i←j}=[x_j - x_i,y_j-y_i]^T pi←j=[xj−xi,yj−yi]T。编队的相对位置参数向量记为 p i ← i = [ p i ← 1 , . . . , p i ← N ] T p_{i←i} = [p_{i←1},...,p_{i←N}]^T pi←i=[pi←1,...,pi←N]T。对于定位为 p 的给定地层,该地层的等效几何形状表示为:

其中, ω = [ Γ ϑ t ] \omega =[\Gamma_\vartheta t ] ω=[Γϑt], Γ ϑ \Gamma_\vartheta Γϑ表示角度 θ ∈ [ 0 , 2 π ) θ∈[0, 2π) θ∈[0,2π)的旋转矩阵, t ∈ R 2 t∈\mathbb{R} ^2 t∈R2表示在 x、y 轴上的平移。
2.多智能体强化学习
相对分布式编队和避障可以看作是一个完全合作的问题,在 MARL 框架下解决。
N 个代理的 MARL 过程可以建模为 N N N个马尔可夫决策过程的扩展 [29]。它由描述所有代理的可能配置的状态空间 S、一组动作 A 1 , A 2 , . . . , A N A_1,A_2,...,A_N A1,A2,...,AN和一组观察值 O 1 , O 2 , . . . , O N O_1,O_2,...,O_N O1,O2,...,ON 组成。
在所有策略梯度方法中,PPO 显示了它在稳定策略和探索最优结果方面的效率。此外,由于其对包括 MAS 在内的各种任务的泛化,它已成为 DRL 最强大的基线算法。在本文的其余部分,文中的方法应用了 MAPPO [25],这是用于多智能体任务的 PPO 的高级版本来解决形成问题。
方法
1.设计奖励函数
RL 最重要的任务之一是奖励函数的设计。提出的奖励函数分为三个部分:相对编队奖励、导航奖励和避障奖励。

其中 α 和 β 是奖励权重的超参数。
相对编队奖励是根据(2)中定义的编队误差设计的。给定一个理想的编队拓扑 q,编队误差 E(̆p, q) 可以用来衡量理想编队与实际编队之间的差异,这是 RL 框架中的一个可优化目标。在所提出的方法中,奖励定义为:
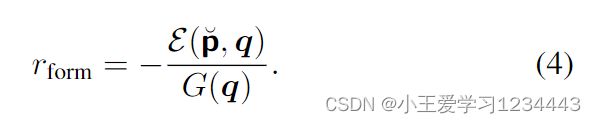
G ( q ) G(q) G(q)是一个归一化因子,仅与理想编队的大小和拓扑结构有关,其中 dij 表示编队中代理 i 和代理 j 之间的距离。引入它来归一化奖励,而不考虑不同的形成规模,避免重复调整超参数 α 和 β。
2.编队适应的策略优化
文中称之为编队适应,即代理需要将自己重新组织成一个新的拓扑结构,以防任何代理断开连接。为了实现编队适应,文中进行了策略蒸馏[32],这是一种整合学习到的策略来处理不同数量的代理以完成编队的方法。例如,如果由 5 个智能体组成的正五边形阵型中的一个智能体因障碍物碰撞而损坏,则其余 4 个智能体需要重新组织成一个正方形才能继续前进。
编队中的最大智能体数设为 N N N,对应的理想编队拓扑为 q N q_N qN。对于参与编队的 n n n个代理 ( n < N ) (n < N) (n<N),文中预设其对应的理想编队拓扑为 q n q_n qn。为了让不同数量的智能体自适应地完成形成,文中根据不同的 n n n和 q n q_n qn训练教师模型。然后文中使用策略蒸馏从教师模型中训练一个可以处理多种情的学生模型。

图中形成适应的政策提炼。观察结果(灰色块用于全零观察填充,绿色块用于真实观察)以及相应的死亡掩蔽输入到教师模型中进行训练。教师模型为学生模型的监督学习生成输入状态和目标输出,其中 KL 散度用作损失函数。
避障课程学习
如第二节所述,优化问题往往是非凸的。直接在复杂环境中训练网络很可能导致不收敛。为了降低训练难度,加快收敛速度,文中采用预定义课程学习的思想[34],设置不同级别的避障难度。
具体课程设置如下: 文中根据障碍物的密度共设置了5个难度级别。一开始,环境中不会放置任何障碍物(0 级)。代理主要专注于学习基本的编队策略和导航到目的地。随着奖励曲线逐渐收敛,难度会增加,不同大小的障碍会逐渐增多出现在环境中。智能体能够学习如何避免到达目的地的障碍以及尽可能稳定地保持理想的编队。设置和结果将在下一节中详细介绍。

上图中使用的演员-评论家网络的模型结构。请注意,文中还使用了诸如观察归一化、层归一化、ReLU 激活等技巧,就像在 [25] 中一样,但为了简单起见,这里不显示。
实验和结果
为了验证文中算法的有效性,将文中的方法与几种基线方法进行了比较,包括 MPC [7]、模糊控制 [9] 和基于 RL 的领导者-跟随者方案 [19] 在多智能体粒子世界环境( MPE) [29]。为了进一步评估文中的方法在物理约束下的实用性,文中不仅开发了一个新的模拟器,称为多车辆环境 (MVE) 3,它支持阿克曼转向模型而不是全向车轮模型,而且还在一个相应的硬件平台。
A.模型配置
在文中的模型中,actor网络和critic网络都依次由3个dense层、1个GRU层和1个dense层组成,如图3所示。dense层和GRU层的隐藏大小设置为是 64。文中遵循 PPO 实施中的常见做法,包括具有优势归一化的广义优势估计 (GAE) [35]、观察归一化、梯度裁剪、层归一化、具有正交初始化的 ReLU 激活。遵循 [36] 提出的 PopArt 技术,文中通过对值估计的运行平均值对值进行归一化,以稳定值学习。
B.MPE 中的仿真结果
场景设置如下: 代理的最大速度限制为 1m/s。代理是边长为 0.01m 的正方形。代理在 x ∈ [−2m, 2m], y ∈ [−2m, 2m] 范围内随机启动,并且目的地将在距离代理初始位置至少 36m 的距离处启动。障碍物是半径在 [0.01m, 0.05m] 之间的圆。障碍物均匀分布在起点 [0m, 0m] 和目的地之间。地图上随机分布的障碍物数量会根据难度的不同而增加。文中在 MPE 中的场景渲染如下图所示

图中多智能体粒子世界环境 (MPE) 中的仿真结果。代理(绿色方块)正在向屏幕外的目的地导航,同时保持队形并避开障碍物(灰色圆圈)。红色光线代表特工装备的激光雷达的视野。
传统控制器(MPC 和模糊控制)将多任务场景视为运动规划问题。每个子任务的所需位置将作为控制器的输入。为了确保复合行为的性能,子任务被分配到具有微调阈值的不同优先级。控制器将在一个时间步执行具有最高优先级的任务。既然安全是第一要务,那么规避行为是重中之重,形成行为是次要的。因此,除非代理进入安全区域并且编队误差收敛,否则不会触发导航行为。避障行为是用基于流的路径规划器设计的。
基于 RL 的领导者-跟随者方案使用与我们的方法相同的网络架构,通过跟踪虚拟领导者来训练代理以形成理想的拓扑。每个代理只负责跟踪其与领导者和障碍物的相对位置,如 [19].

上图显示了不同控制器执行的编队误差和导航奖励的收敛情况。看来,我们的方法在编队精度、收敛速度和处理多任务的能力方面表现出色。具体来说,我们的方法可以收敛到较低的编队误差,这表明在运动过程中可以更好地保持编队。这导航奖励描述了 DRL 方案在处理多任务问题时的优势。随着编队误差的收敛,鼓励编队加速导航,但传统控制器难以在不同行为之间切换。这主要是因为我们的方法联合优化了所有奖励函数,这使得智能体能够在没有任何先验知识的情况下成功学习编队控制和导航之间的优先级。我们的方法还实现了与基线相当的避障成功率,同时实现了更高的移动到目的地的效率。
C.使用 MVE 实现硬件
MVE 中的代理被设计为具有阿克曼转向的智能车辆。与 MPE 中的简化模型不同,我们在实践中考虑了轴距和转向角的约束,这导致了车辆的非零转弯半径。给定轴距 L L L和转向角 ϕ \phi ϕ,转弯半径 R R R可以计算为: R = L ϕ R=\frac{L}{\phi} R=ϕL 。给定后轮的速度 v b v_b vb,方位角 θ θ θ的角速度可以计算为 ω = v b L t a n ϕ ω = \frac{v_b}{L}tan\phi ω=Lvbtanϕ。如果 L L L设置为 0,模型将退化为 MPE,我们可以直接用 v v v和 ω ω ω控制车辆。在 MVE 和硬件实现中,控制变量变为 θ θ θ和 v v v。由于硬件控制系统的限制,我们将控制变量的值离散化。决策频率为1Hz,控制频率为100Hz。在决策阶段,模型给出了理想的 v b v_b vb和 ϕ \phi ϕ。在控制阶段,智能体将尽最大努力达到理想的控制变量。


在硬件实现中,我们使用的场景如图 1 和图 2(a)。多个 Ackermann-steering 代理随机放置在一个房间中。将半径为 0.14m 的圆柱形物体作为障碍物放置在场地中。智能车辆如图2(b)所示。轴距L为0.20m,全宽0.18m,全长0.25m,即与仿真平台完全一致,如图2©所示。最大速度限制为 0.361m/s,最大转向角限制为 0.298rad/s。我们使用 OptiTrack 运动捕捉系统 4 来获取位置的真实情况并给出相关的观察结果,如图 2(d) 所示。代理通过激光雷达检测障碍物。我们进行了几次硬件实验,不同数量的代理在避障环境中形成。可以在以下位置找到演示https://sgroupresearch.github.io/relativeformation/
结论
在本文中,我们开发了一种基于 MAPPO 的分布式编队和避障方法,其中代理仅使用其本地和相关信息来做出运动决策。我们引入了策略蒸馏,以使形成系统在代理意外断开的情况下具有适应性。课程学习也用于简化学习过程。我们的模型在平均编队误差、编队收敛率和避障成功率方面取得了更好的表现。此外,我们还构建了一个新的仿真环境和一个支持阿克曼转向几何的硬件平台,以验证我们算法的可行性。
对于未来的工作,我们将探索大规模分布式形成方法,其中代理不完全连接,只能与邻居获取信息。此外,我们还将专注于开发自研的MVE和相应的硬件平台,以解决MARL算法部署中的sim-to-real问题。