翻译：一个交互式森林(An interactive forest)

一个交互式森林(An interactive forest)

Thomas di Giacomo   
Stéphane Capo
François Faure   
翻译：张嘉华
[email protected]

来源：http://w3imagis.imag.fr/Membres/Thomas.Di-Giacomo/research/egwcas01/，大规模场景系列文章(2)

摘要 (Abstract):

我们展现了一个森林原型，在这个原型里，视频游戏玩家能够移动和物理地和树木进行交互。树木在每次重画的时候过程式on-the-fly构造。两个动画方法联合起来：一个程序方法有效地处理大部分的,一个基于物理的方法允许用户和树木交互。基于物理的方法在需要的地方动态应用。物理数据仅仅在物理方法应用的时候被计算，用完之后就被删除。我们在动画各帧直接实施了平滑过渡。我们在渲染和过程动画中使用了细节层次技术（Levels of detail）。我们的方法允许实时显示包含角色动作和一个256颗树构成的森林的交互式动画。

1. 动机与综述 (Overview and Motivation)

在我们和一家视频游戏公司合作的内容中，我们把显示大量植物场景动画定位为主要的问题。更明确一点就是我们的目标是建模一个交互式森林，玩家能够在森林里移动和进行交互动作，例如夺取一个树枝或者摇动一颗树。这样一个应用程序将会是计算机图形学里的一个挑战，由于几何上动态复杂性。渲染一颗单独的树可能需要过千的三角形面片和自由的角度或者更多。因此，一个森林可能相当复杂以致难以处理。但是，细节层次（LOD）方法能够帮助我们根据元素的可视的贡献度调整元素的复杂度。一颗处于前景的树或许会用一万个多边形建模，而一颗后景的树可能只用100个三角形。对于一个带有固定观察点的应用来说，动态元素和几何结构能力脱离图形流水线预建模，假设我们能够精细化这些元素根据它们可视的贡献度，然后用标准的技术去渲染场景。更困难的问题是，事实上观察点是经常改变，由于细节层次（LOD）需要动态调整，因此我们必须在各LOD之间实施平滑过渡而避免“popping”效果。这应用在几何结构上将会像动画过程一样。

当使用标准的图形硬件进行加速时，渲染复杂度主要依赖于多边形的数量和纹理数据的数量。与之形成鲜明对比，动画复杂度不仅仅是模型中自由度数量的函数，它还依赖于具体使用的方法。过程式方法能够很快速，但是不能保证物理上的合理性，特别是当交互操作发生时。与之形成对比，基于物理的方法生成更加现实的运动，并且允许交互，但是它们通常是需要大量计算的。

在这篇文章里，我们展现了一种渲染整个森林的方法，我们主要的焦点是森林的交互动画。我们的几何模型在每次重画时通过on-the-fly程序计算生成，使用了一个完全定义每颗个体树的小的参数集。这产生了一个非常紧凑的几何数据集。我们使用过程式方法在每个不同的细节层次（LOD）为树木进行动画，以模拟风吹的效果。一个化简的动态的树木模型用于处理用户交互。这些动画方法和我们熟悉的方法都是很接近的。我们主要的贡献是联合了这些方法，使基于物理的动画只在需要的地方使用。物理数据将会动态生成以处理交互和之后的删除。我们在过程式和物理式动画之间进行过渡而避免跃动（popping）效果。结合我们过程式LOD，该方法允许交互森林动画由小于100颗树组成，同时带有独立的视频游戏质量。

本文章剩下的部分是按如下组织的：在第2节，我们介绍过往的相关工作，在第3节，我们大致描述我们的几何建模方法，在第4节介绍我们的动画方法，第5节将介绍我们的结果，最终的总结和未来工作的讨论将在第6节。

2. 相关工作 (Related Work)

2.1动画细节层次技术（LOD for animation）

对于几何结构，动画技术能够调整和简化确定的情况(例如，当运动太快、太远或者对于人的视觉来说无限多[Ber97]，或者当运动对于人来说是很少感兴趣，或者不需要复杂的计算)。尽管 [GCB95] 应用这种方法去产生过程式动画（通过减少运动采用频率，并且以自由的角度衔接角色动作），但显得更适合于应用它到基于物理的动画，因为它需要很高消耗的计算。为了简化或者细化运动，自适应的模型必须建立，并且在保证各个细节层次之间的平滑过渡 [Val99] 。

目前已经能够混合不同模型，或者能够重构一个不同分辨率的模型。多分辨率模型已经得到应用 [CH97] ，用以在三种不同的模型模拟单一点运动，动态的运动学上的单一质点运动，渐变可能仅仅在某一确定时间。[PC01] 通过三个模型模拟一个牧场。三维刀片状草，纹元（texel）和二维纹理通过插入三维运动以匹配需要的纹元。

在单一多分辨率模型工作的方法主要是基于物理的方法：[HPH96] 和 [HH98] 细化mass-spring网络, [DDBC99] 和 [DDCB01] 提议多分辨率FEM 以模拟肝脏的变形。

在这篇文章，我们介绍了一种混合方法使用两种不同的模型，其中一种是多分辨率模型。

2.2 风、树 (Wind, trees)

森林中偶然的风已经有一定的相关研究（[SF92]和[Sta96]），这两种方法都为风使用随机向量域，以及为树对风的响应使用一个枝条摆动分析模型。但是[Sta96]直接合成运动，不考虑综合。我们不能够应用这样一种方法由于我们需要综合。我们生成风带有和[PC01]同样的微元，那就是说二维掩码包含一个向量域，带有速率和影响的区域。

我们和[Ono97]相似，同样简化地假定树木的动力学：树木的密度是一致的，没有树枝和叶子间的碰撞，树枝由弯曲运动，而不是扭转。

3. 几何模型 (Geometrical model)

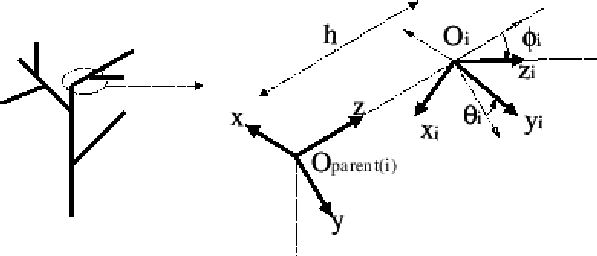
我们的树是由一系列定义了拓扑结构的骨架结点和一些了定义了几何结构的网格组成。骨架结点定义了拓扑结构、树枝的长度和角度。图1展示的几何参数用于定义一个树枝相对于它父结点的位置。子结点的参考系首先进行h大小的平移和沿着z轴相对于父结点角度大小的旋转，接着应用一个沿着y轴，角度为的旋转应用到子结点。

图1：一个树枝i相对于它的父结点决定位置

网格定义了树枝的形状和纹理，为了减少几何数据，骨干结点和网格在每次屏幕刷新时通过一小系列结点需要的参数预计算。种子集完整地定义了森林并且是唯一的参数集。和其它应用中的渐进网格方法相比，我们方法有以下优点：

• 只需要很小的内存消耗就能够生成一整个带有不同类型树木的森林
• 拓扑和几何信息允许我们像外形一样化简拓扑结构
• 平滑度不受参考模型限制，能够达到任意高度

额外的计算消耗被数据流动减少部分得到平衡。此外，平台（Playstation 2, recent PC cards）数量的增加，使用专门的处理器用于网格生成，能够节省大量的计算时间。我们的目标是为游戏以及其它植物应用程序生成具有高度视觉真实感的树木。因此我们作出下面的选择：

• 骨干的生成通过一个图形节目由游戏设计给定的一些参数（大小，子结点的数量，树叶的数量）控制
• 系统使用一些通过对真实树木观察所得的简单的规则，并且不允许改变这些规则。例如，树枝和它的母亲结点之间的最大角度是它们亲缘直径的函数。
• 参数的数量尽可能小。这能够让建模更简单并且减少建模一颗唯一的树所需的数据到小于1k，同时使用Perlin noise去获得更为真实的自然质感。

我们根据元素在屏幕空间的投影大小调整LOD。LOD通过一个全局的因子调整，该因子是上一帧场景整体复杂度的函数。反馈机制允许我们们近似设置全局复杂度到任意的层次。

4. 树木动画 (Tree animation)

我们通过为每一个树枝控制角度和形成树木动画（见图1）。在这一节，我们首先介绍过程式动画方法，然后介绍基于物理的方法，最后介绍上述两种方法相结合后的方法。

4.1 过程式动画 (Procedural animation)

我们的过程式运动是风元（wind primitive）穿越场景的函数。我们首先简单地描述风，然后定义运动方程式，然后应用细节层次技术去产生过程式运动。

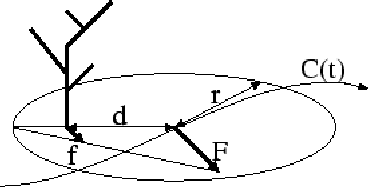
风元（Wind Primitive）：一个风元（wind primitive）（见图2）由一个圆盘（disk）状影响区域、一个力矢量F和一个震动（pulsation）定义。

图2：应用到树木上的一个风元

每个在区域里的树木的树枝受到力f的影响，力f定义如下：

为了简化计算，这里忽略相位角度。圆盘区域能够能够沿着给定的轨道C(t)移动。这种风元允许我们测试我们的框架。在未来的工作，我们会实现更科学的函数。

对风的响应(Response to wind)：我们的过程式方法不是物理的，由于它不是基于由加速度综合得到的时间。但是它设计的目的是用于容易转变到基于物理的方法。每个应用到树枝上的风力产生一个基于它的力矩，是形成转到运动的成因。我们通过下面的公式近似计算力矩：

其中L是树枝的长度，z是它的轴。然后投影力矩到旋转轴以获得一个旋转幅度（rotation amplitude）。运动由风云引起，可以描述如下：

其中和y是树枝相对于父结点的旋转轴（见图1）。m是树枝惯性的近似值（见4.2.1节）。风的动作如此作为一种外力综合了两次。通过对所有应用到树枝上的风元运动求和，得到了该树枝最终得到的值：

角度直接设置到应用的力矩的值。风的方向连同力的大小和pulsation通过力矩投影计算。

细节层次 (Levels of detail)：动画LOD已经独立于渲染技术发展了很长一段时间。对于现在，细节层次涉及深度递归多于屏幕大小。树枝的接缝点是固定的。能够独立地为每颗树设置细节层次。我们的判断标准是基于视深度和风的存在。我们通过在时间间隔(to,t1)间进行线性插值实现过渡渐变：

• 固定的到移动的
• 移动的到固定的

是对风动作的响应，是实际应用的角度。在渐变的期间，能够通过倒转进度值切换回过去的LOD层次。

4.2 基于物理的动画 (Physically-based animation)

基于物理的动画使用物理数据，如力（force）、块（mass）以及硬度（stiffness）。尽管过程式建模不是设计来用于生成这些物理数据，但是我们还是能够通过几何数据建立它。这里，我们首先简要介绍一下如何通过过程式生成几何数据建立一个物理模型，然后介绍一个针对物理动画的简化的方法。

物理模型（Physical model）：正如我们前面提到的，没有物理数据永久保留，我们通过几何数据推导出on-the-fly mass、硬度（stiffness）和阻尼（damping）。和过程式动画相比，我们现在考虑风的动作作为一个真实的力。为了获得一个从程序上导物理上连续的动画，我们应用风作用的第二次衍生物（the second time derivative of wind action），使用当前的风元（wind primitive），我们设定：

由于风带来的运动是这样理论上和程序计算的运动一致。实际上，由于要考虑时间合成因素，不采用阻尼运动会带来分歧。由关节产生的扭矩被用线型阻尼角度弹力（linear damped angular springs）来模拟. 硬度系数k和阻尼系数v是根据枝干的直径和长度来估计的。在线性弹性理论中，硬度与对象区域的翻转有关。对于一个给定的力，整个树枝最后的偏移与它的长度是成正比的。因此，我们设k与成正比，其中d表示枝干的平均直径，l表示枝干的长度。我们一般假定阻尼与硬度成正比。在连接处的扭矩有以下公式给出：

质量与体积有很大的关系。所以我们限制m与成正比。在未来的工作中我们将研究使用，用以模拟一根棒的惯性。

运动方程 (Equations of motion)：为了节省估算时间，我们应用简化的动力学，并且只考虑旋转。动力学的定理如下：

其中表示应用于物体的净力矩。表示物体在世界坐标下的角速度，表示物体的角加速度，J表示物体的惯性矩阵。第二个方程来源于一个简化的假设，其中I表示单位矩阵。

净力矩由风力和连接点力的影响叠加而成：

其中下标p表示枝干的父枝。然后我们将物体相对于父枝的角加速度投影到极坐标中（two rotations axes ），以获得连接点的角加速：

我们使用标准的欧拉方法对时间进行插值：

并且是相同的。为了完成时间合成，帧与帧之间的位置和速度必须保存起来。.

4.3 运动合成（Hybrid animation）

我们使用运动合成来联合风力作用和用户的动作，例如抓住某枝干。我们首先说明这两种形式如何在同一棵树上共存。然后我们将说明如何变换和实现。

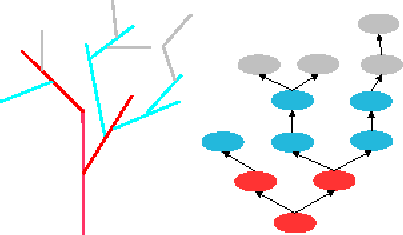
两种方法的共存（Coexistence of the two methods）：过程式动画是利用4.1和4.2所述的方程计算的，不考虑其他枝干的运动。所以程式动画在混合动作中表现力欠佳。基于物理的动画使用力网（net force）计算. 物体的弹力依赖于它的位置和速度。因此对于每个枝干的物理运动，我们必须知道其相邻枝干的位置和速度。如果相邻枝干是物理运动，那么它的速度和位置一样也是它运动状态的一部分。如果它是程式运动，我们则用有限个不同的来计算。图3举例说明了一个树混合的方法。

图3: 运动合成。底部的红色枝干为物理运动。中部的蓝色枝干为程式运动。高层的灰色枝干为混合运动。

两种方法间的转换(Transitions between the two methods)：程式运动向物理运动的转换可以通过程式的位置计算和速度演绎即时完成。但是，物理运动向程式运动的即时转换会引起效果跃动，因为程式运动的位置是有一个与时间相关的函数生成的，不考虑先前的位置和速度。因此我们同时计算两种运动并且在时间间隔内做一个平滑混合，例如1.5秒。转换于时刻开始并于时刻结束。对于给定的时间间隔我们使用0到1的平滑系数：

其中波浪线上标表示动作使用程式方法计算，横线上标表示动作使用物理方法计算。在任何时刻，我们可以利用的变化转回基于物理的动作。

5. 结果 (Results)

这里我们展现一些视频截图，它们描述了我们方法的不同特征。视频能够通过以下地址下载：

http://www-imagis.imag.fr/~Thomas.Di-Giacomo/research/egwcas01/index.html

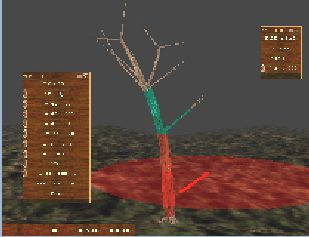
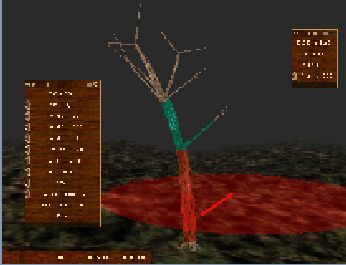
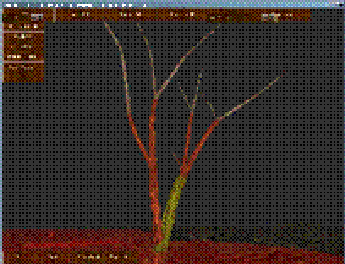
• 一颗树带有细节层次的过程式动画。树木的运动根据方向、大小和在风的影响区域内的位置预计算（这些区域是图4a中的红色圆圈）。我们能够简化或者细化树枝动画的深度层次（图 4a中红色的分枝），为了确保平滑过渡（以绿色展现），渐变能够进行通过增加渐变的时间间隔加以调整以得到平滑度。
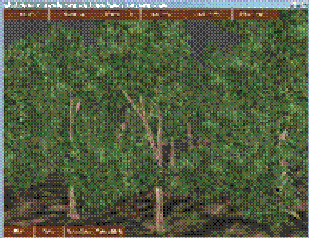
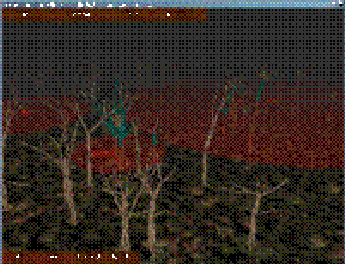
• 过程式动画森林（图4b，4c）。我们选择下面标准对于每一个细节层次：如果树不在风的影响范围，它的细节层次为0，并且树不移动。细节层次根据流入的风的数量、与摄像机的距离以及树木在影响区域内的位置细化。图4c展示了我们通过细节层次技术（LOD）得到了27fps的交互帧速，在没有LOD的情况下只有1fps对于同样的场景。
• 单颗树木的基于物理的动画。所有的分枝都是物理处理的，展示了分枝在一阵风之后回到它们原来的位置。这种效果主要是通过校准物理参数以响应风来完成的。（见视频）
• 树木的混合动画。我们能够联合两种方法（带有渐变的过程式方法和基于物理的固定的方法）。我们得到了从过程式到物理式切换一根树枝运动的连续性。渐变能够像本文前面所述一样得到处理（见视频）。
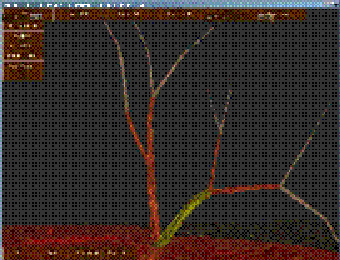
• 力和风施加到一颗树上。我们施加了一个手动定制的力到一个选定的树枝（图4d中黄色的树枝，4e被扯下来）。当树木受到风的影响，我们在树枝被捕获时在同样的深度层次设置物理LOD。因此，该运动是风的作用和力的作用的联合。
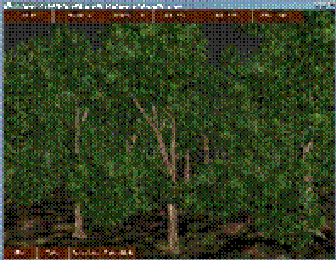
• 整个森林。最终我们完成了包含256颗树的整个森林的动画（图4f）,在需要的地方施加物理。我们能够选择场景的任意树枝，并且和它进行交互。

a	b	C
d	e	f
图4：结果

6. 讨论 (Discussion)

我们呈现了一个交互森林的原型。它由on-the-fly构造的树木构成，在每次重画时通过一系列参数定义位置、拓扑结构和外形。该方法减少了内存需求并且允许很好的转换细节层次。我们已经开发出一个新的动画方法很好地适应这种方法。它联合一个快速的过程式方法包含各细节的层，带有基于物理的模型，用于处理交互。能够在任意时间实施动画之间的渐变。物理方法仅仅在需要的时候动态应用。作为结果，我们得到了高的帧速和交互性。

对于特定的需要还需要对方法进行发展和应用。实际的动画需要比我们现在基于层次的方法更好的树木的区分。我们将会增强过程式和物理式方法，更多的值得探讨的风元将会添加实施，隐式的插值将会施加到硬的物体上。我们同时还计划研究噪声函数以处理树枝以外的叶子动画。碰撞检测也是我们下一步考虑的工作。

从一个更基础的观点来看,我们将来会研究如何让过程式和基于物理的方法共存。在我们当前的实现，物理分枝是程序生成那些分枝的双亲。相反同样也应该成立，例如，如果一个一只小鸟停靠于一个小的树枝上，我们不一定需要物理地让该父亲结点树枝表演动画，仅仅那些真正受到小鸟影响的需要表演动画。更一般地，我们需要准则去决定那些树枝需要物理动画，我们同时计划应用LOD到基于物理的动画，也许使用子树聚类（sub-tree clustering）。

参考文献 (Bibliography)

Ber97

R. Berka.
Reduction of computations in physic-based animation using level of detail.
In Spring Conference of Computer Graphics, 1997.

CH97

D. Carlson and J. Hodgins.
Simulation levels of detail for real-time animation.
In Graphics Interface, 1997.

DDBC99

G. Debunne, M. Desbrun, A. Barr, and M.-P. Cani.
Interactive multiresolution animation of deformable models.
In Computer Animation and Simulation, Sep. 1999.

DDCB01

G. Debunne, M. Desbrun, M.-P. Cani, and A. Barr.
Dynamic real-time deformations using space and time adaptive sampling.
To appear in the SIGGRAPH'01 conference proceedings, 2001.

GCB95

J. P. Granieri, J. Crabtree, and N. I. Badler.
Production and playback of human figure motion for visual simulation.
Modeling and Computer Simulation, 5(3):222-241, 1995.

HH98

P. Howlett and W. T. Hewitt.
Mass-spring simulation using adaptive non-active points.
Computer Graphics Forum, pages 345-354, 1998.

HPH96

D. Hutchinson, M. Preston, and T. Hewitt.
Adaptative refinement for mass-spring simulations.
In Eurographics Workshop on Animation and Simulation, pages 31-45, Sep. 1996

Ono97

H. Ono.
Practical experience in the physical animation and destruction of trees.
In Eurographics Workshop on Animation and Simulation, pages 149-159, Sep. 1997.
Industrial Light and Magic.

PC01

F. Perbet and M.-P. Cani.
Animating prairies in real-time.
In Symposium on Interactive 3D Graphics, 2001.

SF92

M. Shinya and A. Fournier.
Stochastic motion-motion under the influence of wind.
j-CGF, 11(3):C119-C128, C469, sept 1992.

Sta96

J. Stam.
Stochastic dynamics: Simulating the effects of turbulence on flexible structures.
Technical Report RR-2847, INRIA Rocquencourt, March 1996.

Val99

Bernard Valton.
Gestion de la complexite de scenes animees et interactives : contributions a la conception et a la representation.
PhD thesis, Univ. de Rennes(FR), 1999.