2.qt-Cyrus-Beck算法(凸多边形的线裁剪算法-C++实现)

该算法比Cohen-Sutherland算法复杂不少, 它允许对非矩形窗口进行线剪裁。它还消除了Cohen-Sutherland算法中所需的重复计算

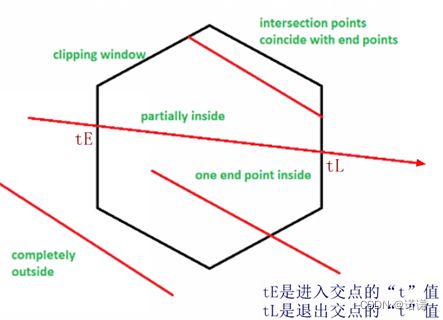
如下图所示:

如果线段部分位于凸多边形中或者完全在凸边形中,那么必定:
0 <= tE <= tL <= 1
如果线段位于凸边形外部,那么:
tL < tE

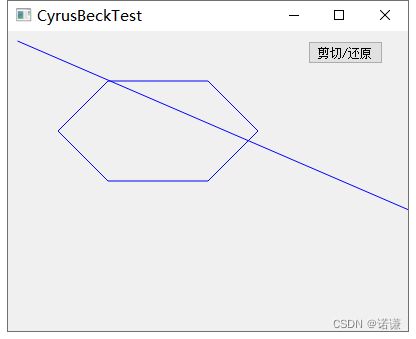
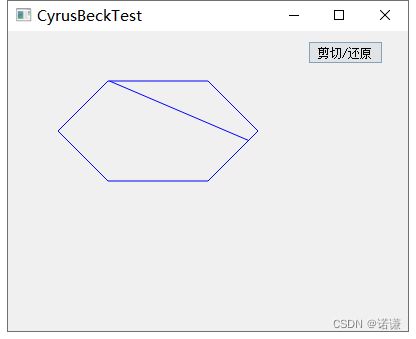
demo如下所示:

 

实现逻辑如下所示:
1.计算每条边的法线。
2.计算剪裁线的向量。
3.计算每个边顶点与剪切线的向量与边的法线之间的点积（对于所有边）。
4.计算剪裁线向量与所有边缘的法线之间的点积,为正则为入点、否则为出点
5.从每组中选择一个't'值，并将其放入线的参数形式中以计算坐标。

代码如下所示:

#include "widget.h"
#include 
#include 
#include 



// 点乘
int dot(QPoint p0, QPoint p1)
{
    return p0.rx() * p1.rx() + p0.ry() * p1.ry();
}

float max(QVector t)
{
    float maximum = INT_MIN;
    for (int i = 0; i < t.size(); i++)
        if (t[i] > maximum)
            maximum = t[i];
    return maximum;
}

float min(QVector t)
{
    float minimum = INT_MAX;
    for (int i = 0; i < t.size(); i++)
        if (t[i] < minimum)
            minimum = t[i];
    return minimum;
}

// Cyrus Beck函数
bool CyrusBeck(const QVector& vertices,const QLine& lineSrc, QLine& outLine)
{
    int n = vertices.length();
    QVector normal(n);
    QPoint line[2] = {lineSrc.p1(), lineSrc.p2()};

    // 1.计算每条边的法线
    for (int i = 0; i < n; i++) {
        normal[i].ry() = vertices[(i + 1) % n].x() - vertices[i].x();
        normal[i].rx() = vertices[i].y() - vertices[(i + 1) % n].y();
    }

    // 2 计算剪裁线(P0->P1)的向量
    QPoint P0_P1 = QPoint(line[1].rx() - line[0].rx(), line[1].ry() - line[0].ry());

    QVector P0_PEi(n);

    // 计算所有边的P0 -> PEi的向量值(计算每个边顶点与剪切线的向量)
    for (int i = 0; i < n; i++) {

        P0_PEi[i].rx() = vertices[i].x() - line[0].rx();

        P0_PEi[i].ry() = vertices[i].y() - line[0].ry();

    }

    int  numerator[n], denominator[n];

    //计算分子和分母
    //使用点乘函数
    for (int i = 0; i < n; i++) {
        numerator[i] = dot(normal[i], P0_PEi[i]);
        denominator[i] = dot(normal[i], P0_P1);

    }

    float t[n];

    QVector tE, tL;

    for (int i = 0; i < n; i++) {

        t[i] = (float)(numerator[i]) / (float)(denominator[i]);

        if (denominator[i] > 0)
            tE.push_back(t[i]);
        else
            tL.push_back(t[i]);
    }

    // 初始化't'的最后两个值tE tL
    float temp[2];

    // 取所有TE和0的最大值，最大值为0
    tE.push_back(0.f);
    temp[0] = max(tE);

    // 取所有Tl和1的最小值，最小值为1
    tL.push_back(1.f);
    temp[1] = min(tL);


    // 进入的t值如果>退出的t值,则说明在凸多边形外
    if (temp[0] > temp[1]) {
        return false;
    }

    // 计算获取到的坐标
    outLine.setP1(QPoint(
                (float)line[0].rx()  + (float)P0_P1.rx() * (float)temp[0]
                ,(float)line[0].ry() + (float)P0_P1.ry() * (float)temp[0]
                ));

    outLine.setP2(QPoint(
                 (float)line[0].rx() + (float)P0_P1.rx() * (float)temp[1]
                ,(float)line[0].ry() + (float)P0_P1.ry() * (float)temp[1]
                ));

    qDebug()<<"计算获取到的坐标" << outLine;
    return true;
}


QVector vertices
    = { QPoint(290, 50),
        QPoint(150, 100),
        QPoint(290, 150),
        QPoint(100, 150),
        QPoint(50, 100),
        QPoint(100, 50) };

QLine line = QLine(QPoint(10, 10), QPoint(450, 200));

//QVector vertices
//    = { QPoint(290, 50),
//        QPoint(150, 100),
//        QPoint(290, 150),
//        QPoint(100, 150),
//        QPoint(50, 100),
//        QPoint(100, 50) };

//QLine line = QLine(QPoint(140, 24), QPoint(340, 220));

QLine lineChanged;
bool trigger = false;

Widget::Widget(QWidget *parent)
    : QWidget(parent)
{
    QPushButton* btn = new QPushButton(this);
    btn->setText("剪切/还原");
    btn->move(300,10);
    this->resize(400,300);

    connect(btn, &QPushButton::clicked, this, [&]{

        trigger = !trigger;
        update();

    });


    CyrusBeck(vertices, line, lineChanged);

}

Widget::~Widget()
{

}

void Widget::paintEvent(QPaintEvent *)
{
    QPainter painter(this);
    painter.setRenderHint(QPainter::Antialiasing, true);
    painter.setPen(Qt::blue);

    painter.drawPolygon(QPolygonF(vertices));

    if (trigger) {
         painter.drawLine(lineChanged);
    }
    else {
        painter.drawLine(line);
    }

}