用凯泽窗设计FIR滤波器的优点

一、理论基础

之前介绍过的任何一个窗，其参数都是固定的，都不能同时实现窗函数的几个指标的优化。因此，需要根据应用不同，选择不同的窗函数。而凯泽窗可通过调节窗函数的参数在各指标之间进行折中。
凯泽窗函数的时域表示为

式中：I。(·)是零阶贝塞尔函数；用于调节窗函数的形状和指标。下图所示为凯泽窗函数两个不同B值时的时域波形（N=51）。

当β=0时，凯泽窗相当于矩形窗；当=5.44时，凯泽窗相当于海明窗；当β=8.5时，凯泽窗相当于布莱克曼窗。选择不同的β值即可得到不同的频域特征。Kaiser经过大量数值实验得到了一组设计数字滤波器凯泽窗参数估计公式，即估算N和β值。
N的计算公式为

式中：△f为归一化的过渡带宽，△f=（ws一wp)/2π。
β的计算公式为

式中：As是阻带衰减（单位为dB）。

凯泽窗函数的时域波形

 

5种窗函数的特性表

在上表中给出了5种常用的窗函数在某一个窗长N时，除凯泽窗以外其他窗函数的系数都是固定的，而凯泽窗的系数不是固定的，而是随参数beta值而变化的，从上图中可看到不同的β值时凯泽窗函数有不同的形状。

凯泽窗在通带波纹和阻带衰减都随参数beta值而变化，下表中列出了部分β值与FIR滤波器性能的关系。

从上表中可看出，当参数B取不同数值时，阻带的衰减可以从30dB增加到100dB，滤波器的性能与参数β的关系极为紧密。所以在滤波器设计中一定要选择合适的参数β值，使滤波器为最佳。

二、案例：采样频率为100Hz,通带频率fp=3Hz，阻带频率fs=5Hz，而通带波纹Rp=3dB，阻带衰减As=50dB，在本案例中用凯泽窗。程序如下：

clear all; clc; close all

Fs=100;                                 % 采样频率
Fs2=Fs/2;                               % 奈奎斯特频率
fp=3; fs=5;                             % 通带和阻带频率
Rp=3; As=50;                            % 通带波纹和阻带衰减
delta1 = (10^(Rp/20)-1)/(10^(Rp/20)+1); % 求通带波纹线性值
delta2 = (1+delta1)*(10^(-As/20));      % 求阻带衰减线性值
f=[fp fs]/Fs2; A=[1 0];                 % 设置频率指标f和幅值指标A
dev=[delta1 delta2];                    % 设置偏离指标dev
[N,Wn,beta,ftype] = kaiserord(f,A,dev); % 用kaiserord函数计算阶数和其他参数
N=N+rem(N,2);                           % 保证滤波器系数长N+1为奇数
b=fir1(N,Wn,kaiser(N+1,beta));          % 用fir1函数凯泽窗函数设计FIR第1类滤波器
[db,mag,phs,gdy,w]=freqz_m(b,1);        % 计算滤波器频域响应
% 作图
subplot 211; plot(w*Fs/(2*pi),db,'k','linewidth',2);
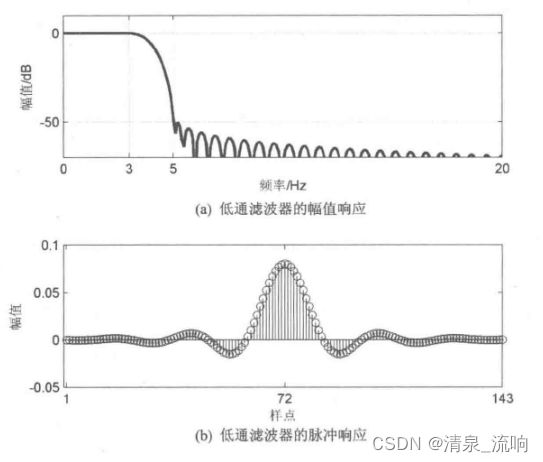
title('低通滤波器幅值响应');
grid; axis([0 20 -70 10]); 
xlabel('频率/Hz');  ylabel('幅值/dB')
set(gca,'XTickMode','manual','XTick',[0,3,5,20])
set(gca,'YTickMode','manual','YTick',[-50,0])
subplot 212; stem(1:N+1,b,'k');
title('低通滤波器脉冲响应');
xlabel('样点');  ylabel('幅值')
axis([0 N+1 -0.05 0.1]); %grid;
set(gca,'XTickMode','manual','XTick',[1,(N+2)/2,N+1])
set(gcf,'color','w');

运行结果如下：

分析：

①相同设计指标下，用海明窗，此时最小阻带衰减小于50dB，用凯泽窗，最小阻带衰减刚好达到50dB，满足设计要求。
②相同设计指标下，用海明窗，滤波器长167，而用凯泽窗后滤波器长143，而且衰减更大。因此，在同样满足设计要求的条件下，用凯泽窗时滤波器的阶数，或滤波器系数的长度更小，这能减小滤波过程的运算量，这也是凯泽窗的主要优点。

参考文献：MATLAB数字信号处理85个实用案例精讲——入门到进阶；宋知用（编著）