轻量级神经网络算法系列文章-MobileNet v2
4. 轻量级神经网络算法目录
- 轻量级神经网络算法
4.1 各轻量级神经网络算法总结对比
4.2 SqueezeNet
4.3 DenseNet
4.4 Xception
4.5 MobileNet v1
4.6 IGCV
4.7 NASNet
4.8 CondenseNet
4.9 PNASNet
4.10 SENet
4.11 ShuffleNet v1
4.12 MobileNet v2
4.13 AmoebaNet
4.14 IGCV2
4.15 IGCV3
4.16 ShuffleNet v2
4.17 MnasNet
4.18 MobileNet v3
深度学习知识点总结
专栏链接:
https://blog.csdn.net/qq_39707285/article/details/124005405
本专栏主要总结深度学习中的知识点,从各大数据集比赛开始,介绍历年冠军算法;同时总结深度学习中重要的知识点,包括损失函数、优化器、各种经典算法、各种算法的优化策略Bag of Freebies (BoF)等。
本章目录
- 4. 轻量级神经网络算法目录
-
- 4.12 MobileNet v2
-
- 4.12.1 简介
- 4.12.3 关键点
- 4.12.4 线性瓶颈(Linear Bottlenecks)
- 4.12.5 倒残差(Inverted residuals)
- 4.12.6 模型结构
- 4.12.7 总结
论文《MobileNetV2: Inverted Residuals and Linear Bottlenecks》。
4.12 MobileNet v2
4.12.1 简介
本文提出一个新的结构MobileNet v2,它专门为移动和资源受限的环境量身定制,在各项任务中都取得最佳表现。
MobileNet v2基于反向残余结构(inverted residual structure),其中快捷连接在薄瓶颈层之间。中间层expansion layer使用轻型深度卷积(depthwise conv)来过滤非线性源的特征。并且研究发现,为了不丢失重要特征,去除窄层中的非线性层。
4.12.3 关键点
- 具有线性瓶颈的反向残差
该模块将低维压缩特征作为输入,首先将其扩展到高维,并使用轻量级深度卷积(depthwise conv)进行滤波。特征随后被投影回低维层中。 - 使用线性表达(低维层不使用ReLU等非线性激活函数)
该卷积模块特别适用于移动设计,因为它允许通过从不完全物化大的中间张量来显著减少推理过程中所需的内存占用。这减少了许多嵌入式硬件设计中对主存访问的需求,这些设计提供了少量非常快速的软件控制高速缓存。
4.12.4 线性瓶颈(Linear Bottlenecks)
长期以来,人们一直认为神经网络可以把感兴趣的特征可以嵌入到低维子空间,换句话说,当我们观察特征图的每个单独通道像素时,关键有用的特征实际存在于某些编码后的像素值中,这些关键的值又可嵌入到低维子空间中。乍一看,这样的观念可以通过简单地降低层维度从而降低操作空间的维度来捕捉和利用。MobileNetV1已经成功利用了这一点,通过宽度系数参数在计算量和精度之间进行有效权衡,这一观念已被纳入其他网络的有效模型设计中(例如ShuffleNet)。
根据这种观念,宽度系数方法允许减少激活空间的维数,直到感兴趣的土整流形充满整个低维空间。然而,深度卷积神经网络实际上往往跟有非线性的变换(例如ReLU),这种观念就有问题了。
很容易看出,如果层转换的结果ReLU(Bx)具有非零体积S,映射到内部S的点通过输入的线性变换B获得,从而表示输入空间中对应于全维输出的部分被限制为线性变换。换句话说,深度网络仅在输出域的非零部分具有线性分类器的能力。
另一方面,ReLU在通道降维操作中,它不可避免地丢失该信道中的信息。但是,假如我们有很多通道,并且在激活特征值中有一种特殊结构,可以表达丢失的信息,那么信息可能仍然保留在其他通道中。如果输入特征流可以嵌入到激活空间的低维子空间中,那么ReLU变换在将所需复杂度引入可表达函数集的同时保留了信息。
综上所述,强调了两个属性,这两个属性表明了感兴趣的特征流形可以由高维激活空间流入低维子空间中的要求:
- 如果感兴趣的特征流形在ReLU变换后保持非零体积,则它相当于线性变换。
- 仅当输入特征流形由高维嵌入到低维子空间时,ReLU能够保存关于输入特征流形的完整信息。
有这两个属性可知,假设感兴趣的特征流形是低维的,可以通过在卷积块中插入线性瓶颈层(linear bottleneck layer)(1×1卷积升维操作)来捕获它。实验也表明,使用线性层至关重要,因为它可以防止非线性破坏太多信息。
在本文的其余部分,将利用瓶颈卷积。将输入瓶颈的大小与内部大小之间的比率称为扩展比(expansion ratio)(就是中间升维的维度与输入维度的比值)。
小结:特征流从高维到低维嵌入(例如MobileNet v1中1×1的pw conv),后面再加上ReLU时,可能会造成信息的丢失或者破坏。去掉最后深度可分离卷积中pw卷积的ReLU。
4.12.5 倒残差(Inverted residuals)
Bottleneck block看起来类似于residual block,其中每个块包含一个输入,然后是几个瓶颈,然后是扩展。同样也采用残差块中类似的残差连接。如下图展示了Bottleneck block和残差块的示意图,插入快捷方式的动机与经典残差连接的动机类似:希望提高梯度在乘数层之间传播的能力。另外,反向设计的内存效率要高得多,并且效果也好。
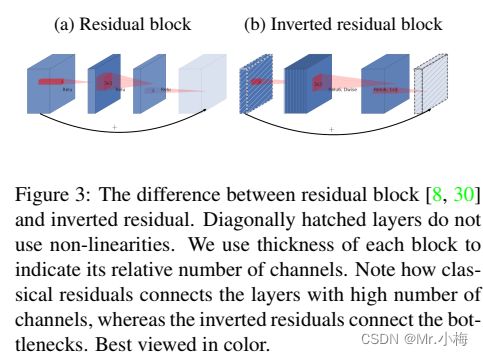
瓶颈卷积的运行时间和参数计算:
基本实现结果如下表所示,一个block size=h×W,expansion factor=t,卷积核k,输入通道数d`,输出通道数d``
MAdds=h×w×d`×t×(d`+k^2+d``)
与深度可分离卷积的MAdds
MAdds=h×w×d`×(k^2+d``)
相比,这个表达式有一个额外的项,因为确实有一个附加的1×1卷积(升维操作),但是网络的性质允许利用更小的输入和输出维度。

小结:经典的残差块(residual block)的过程是:1x1(降维)–>3x3(卷积)–>1x1(升维), 但深度卷积层(Depthwise convolution layer)提取特征限制于输入特征维度,若采用残差块,先经过1x1的逐点卷积(Pointwise convolution)操作先将输入特征图压缩,再经过深度卷积后,提取的特征会更少。所以mobileNetV2是先经过1x1的逐点卷积操作将特征图的通道进行扩张,丰富特征数量,进而提高精度。这一过程刚好和残差块的顺序颠倒,这也就是倒残差的由来:1x1(升维)–>3x3(dw conv+relu)–>1x1(降维+线性变换)。
4.12.6 模型结构
MobileNetV2的结构包含初始的全卷积层,总共32个filters,包含19个residual bottleneck layer。使用ReLU6作为非线性激活函数,因为当用于低精度计算时,它具有鲁棒性。使用核大小为3×3作为网络的标准,并在训练过程中使用Dropout和BN。除第一层外,在整个网络中使用恒定的扩展比率,实验表明,5到10之间的扩展速率导致几乎相同的性能曲线,较小的网络在较小的扩展速率下性能更好,而较大的网络在较大的扩展速率时性能更好。
一般情况下使用6的扩展因子应用于输入张量的大小,例如,对于采用64通道输入张量并产生128通道张量的瓶颈层,中间扩展层为64·6=384通道。
具体网络结构如下表所示:
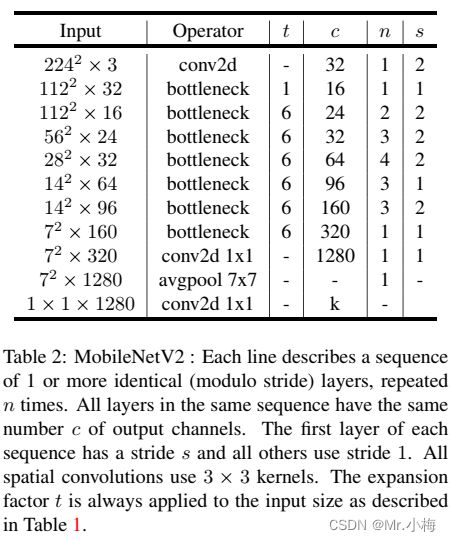
主要网络 (width multiplier 1, 224 × 224)有300M MAdds计算量和3.4M参数量。实验探讨了输入分辨率从96到224以及宽度乘数从0:35到1:4的性能权衡,网络计算成本范围从7M到585MADS,而模型大小在1.7M到6.9M之间变化。
MobileNet v2的InvertedResidual代码实现:
# args(inp, oup=c*width_mult, stride,expand_ratio=t)
hd = int(round(inp * expand_ratio))
layers = []
if expand_ratio != 1:
# expansion layer(pw)
layers.append(nn.Conv2d(inp, hd, kernel_size=1, stride=1, padding=1, bias=False))
layers.append(nn.BatchNorm2d(inp))
layers.append(nn.ReLU(inplace=True))
# dw
layers.append(nn.Conv2d(hd, hd, kernel_size=3, stride=stride, padding=1, groups=hd, bias=False))
layers.append(nn.BatchNorm2d(hd))
layers.append(nn.ReLU(inplace=True))
# pw-linear
layers.append(nn.Conv2d(hd, oup, kernel_size=1, stride=1, padding=0, bias=False))
layers.append(nn.BatchNorm2d(oup))
# 当s==1,inp=oup时,使用残差
4.12.7 总结
- 在MobileNet v1中采用深度可分离卷积,主要包含DW(深度卷积)和PW(逐点卷积),且两者之后都接有ReLU,因为PW会做降维操作,再使用ReLU可能会导致关键特征丢失,所以在PW之后不再使用ReLU操作。
- MobileNet v2中引入残差块,普通残差会先进行1×1降维-然后卷积-最后再进行1×1升维,类似于1中所述,流入到深度可分离卷积的特征图降维操作可能会导致关键特征丢失,所以MobileNet v2中把残差块的顺序颠倒了一下变成,1×1升维-DW卷积-1×1降维(即PW卷积),即Inverted residuals。

