Dilated Convolution(空洞卷积、膨胀卷积)详解

 

作者简介：秃头小苏，致力于用最通俗的语言描述问题

往期回顾：目标检测系列——开山之作RCNN原理详解    目标检测系列——Fast R-CNN原理详解   目标检测系列——Faster R-CNN原理详解

近期目标：拥有10000粉丝
支持小苏：点赞、收藏⭐、留言

 

Dilated Convolution(空洞卷积、膨胀卷积)详解

写在前面

​  首先，来谈谈我是如何一步步接触Dilated Convolution （后文都叫空洞卷积了）的。在一次机缘巧合下，我恰巧瞅到师姐的论文，上面就闪晃晃的写有空洞卷积四个大字，我当时想的是这是什么玩意，听名字有点高大上，于是课下就搜了搜，发现还是挺有意思的，但也一直没有详细的看过，只能说有一个大致的了解，知道这家伙是干什么的。后面是在一门叫学科前言讲座的课程上，听同学提及了这个空洞卷积，讲的非常详细，也谈到了空洞卷积的一些缺陷和解决方法，我记得我当时还问了一些问题，当时觉得这门课程挺累的，但现在回头来看还是很有价值的。最后就是今天较全面的学习了空洞卷积的知识，即将分享给大家。

  这篇文章呢，还是主要参考了霹雳吧啦Wz关于此部分的视频。讲的非常透彻，但是可能由于视频时长等原因，一些点视频中描述的还是不详细的，这里我还是建议大家时间允许的话可以先看看视频，对应视频中有所困惑的地方再来这篇文章找找思路。当然了，如果你想快速的掌握空洞卷积，我认为看这篇文章也足够了。

  准备好了吗，我们这就发车。

 

何为空洞卷积✨✨✨

​  什么是空洞卷积呢，我先不给你说，先来看看我们正常的卷积操作是怎样的，如下图所示：

​  上图展示了一般卷积的过程，其卷积核大小为3×3，步长s=1。

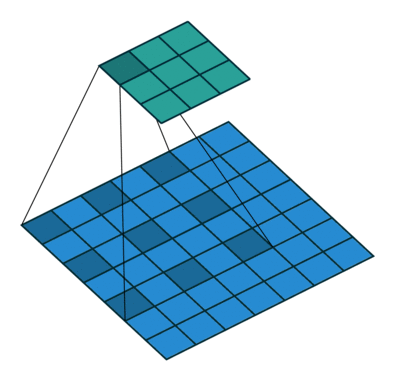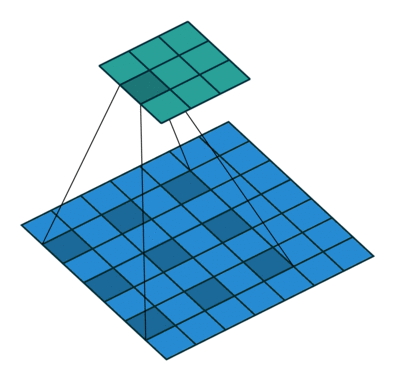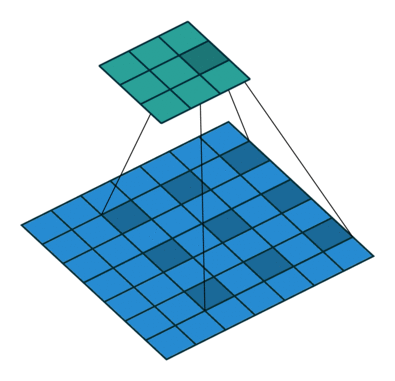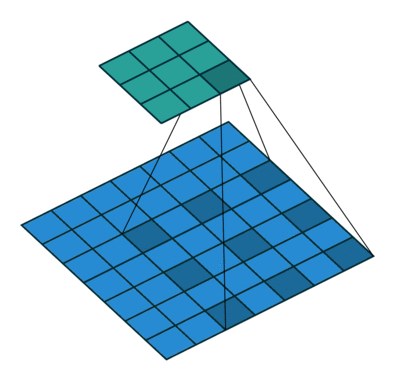
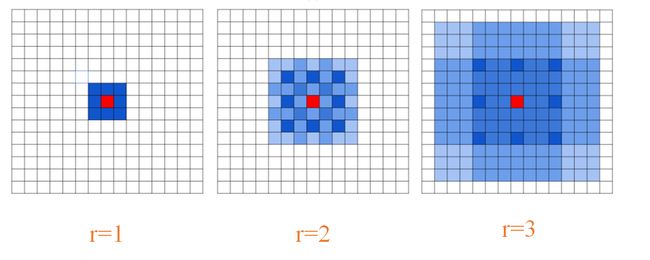
  看完了熟悉的卷积操作，接着我们来看看何为空洞卷积，如下图所示：

  上图展示了空洞卷积的过程，其卷积核大小为3×3，步长s=1，r=2。你或许会问了，这个r是什么呢，其实啊，这个r正是普通卷积和空洞卷积的差别所在，我们称之为膨胀因子。当r=1时，表示卷积核各元素之前没有空隙，即相邻两个元素间位置相差1，此时其实就是我们正常的卷积，所以广义上说，普通的卷积是一种特殊的空洞卷积；当r=2时，表示卷积核各元素之前有一个空隙，即相邻两个元素间位置相差2，此时就是我们上图中的卷积核，为方便大家理解，我把上图r=2时的卷积核提取出来，如下图所示：

​   当然了当r=3、r=4都是同样的道理，这里就不过多叙述了。

 

为何要用空洞卷积✨✨✨

​   我们知道了什么是空洞卷积，自然想要问我们为什么要用空洞卷积呢？其实使用空洞卷积最主要的用途就是增大感受野。enmmm，保姆级教学，我先来为大家介绍一下什么是感受野？感受野就是指特征图上的一个像素对应原图多少尺寸的像素，我画一个简单的图来为大家解释一下：

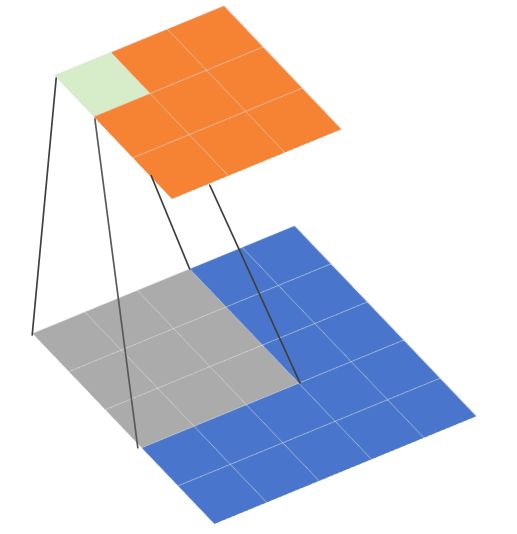
​   上图是一个普通卷积的过程，卷积核大小为3×3，步长s=1。可以发现，所得特征图中一个1×1像素区域（灰绿色）对应了原图中的3×3大小的区域，这就是3×3大小卷积核的感受野。

​   我们再来看，当我们对刚刚得到的特征图（橙色）再经过一次3×3卷积，如下图所示：

​   很显然，此时最后一层特征图中一个1×1像素区域（青蓝色）对应了橙色特征图中的3×3大小的区域，这也是3×3大小卷积核的感受野。

​   那么，现在我将上述两步放在一起，如下图所示：

​   那么请问，此时最后一层特征图中一个1×1像素区域（青蓝色）对应原图多少尺寸大小的区域呢？答案是5×5，因为青蓝色像素感受野包含了整个橙色的区域，而整个橙色区域的感受野正是下方5×5区域大小的范围。【这里应该也好理解吧，大家可以自己动手画画理解理解】

​   通过上文叙述，我们知道了感受野是怎么计算的了，下面给出计算感受野的公式，如下：

​
$$F_i=(F_{i-1}-1)\times stride+k$$

​   其中，$F_i$表示第$i$层的感受野，$F_{i-1}$表示$i-1$层的感受野，$srtide$表示步长，$k$表示卷积核大小。我们可以将公式代入到上面的例子中验算一下是否正确。首先，蓝色、橙色、青蓝色特征图分别表示3层、2层、1层，现我们要计算1层相对于3层的感受野，首先我们要计算出1层对于2层的感受野，即

​ $$F_2=(F_1-1)\times 1+3=(1-1)\times 1+3=3$$

​   得到了$F_2$，我们就可以计算1层相对于3层的感受野，即

​ $$F_3=(F_2-1)\times 1+3=(3-1)\times 1+3=5$$

【注：对于感受野，我觉得很有必要很大家强调一点，即我们所说的感受野都是相对于原图说的，即某层特征图中一个像素尺寸对应原图多少像素尺寸】

---

​   我想通过上文的解释，大家对感受野的计算已经有所了解了。再回到本节的问题上——为什么要使用空洞卷积。使用空洞卷积一个关键原因就是可以增大感受野，这样在检测、分割任务中就能对大尺寸物体表现出较好的效果。至于空洞卷积为什么可以增大感受野，我觉得也非常好理解啊，如下图所示：

​   上图表示使用3×3的卷积核进行空洞卷积，r=2，很明显，此时灰色特征层的感受野为5×5。其实呢，计算空洞卷积感受野也有公式，我们这样来思考，上图是3×3的卷积核，r=2，这样构成的一个空洞卷积核（乱起的名字哈，不用在意）的尺寸就相当于是5×5大小了，这时候我们感受野的计算就相当于5×5卷积核的感受野了。既然这样，我们能否找到空洞卷积核大小和原始卷积核大小的关系呢？当然可以啦，如下：

​ $$k^{\prime }=k+(k-1)(r-1)$$

​ $k^{\prime }$表示空洞卷积核大小，$k$表示原始卷积核大小，$r$表示膨胀因子。大家可以试着将这个公式代入进去，验证公式的正确性！！！既然有了$k^{\prime }$，我们就可以利用原来计算感受野的公式得到计算空洞卷积感受野的公式了，如下：

​ $$F_i=(F_{i-1}-1)\times stride+k^{\prime }=(F_{i-1}-1)\times stride+k+(k-1)(r-1)$$

​   这里大家就自己验证了喔，好好琢磨琢磨，后面会用到这个知识点！！！

 

空洞卷积存在的缺陷✨✨✨

​   上文谈及了空洞卷积可以增大感受野，这是空洞卷积本身的优势。那空洞卷积是否有缺陷呢？关于这点大家可以看看这篇论文，该篇论文就主要介绍了空洞卷积存在的缺陷以及解决方案。

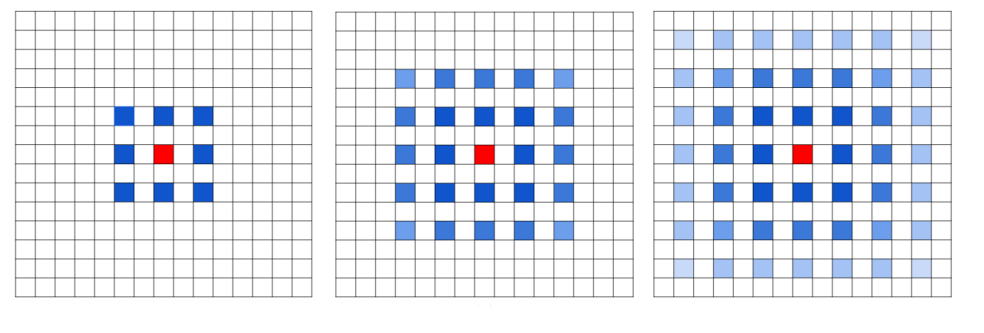
​   其实啊，空洞卷积的缺陷主要体现在存在网格效应，我们可以来看一下下图：

​   上图的卷积核大小都是3×3，r=2。第一次空洞卷积后的感受野为5×5，第二次空洞卷积后感受野大小为9×9，第三次空洞卷积后感受野大小为13×13。【这很容易得到，大家套我上文给出的公式即可】

​ 我们可以看到，连续使用三次r=2的空洞卷积会导致中间有很多空格，即很多像素没有利用到，这会导致出现网格效应，我们拿语义分割为例，如下图所示：

​   可以看到，在分割结果中存在很多很多的不连续的小网格区域，这就是网格效应，也是空洞卷积带来的副作用。

​   我们再来看看本小节的第一张图，你可以发现，小网格上颜色的深度是不一致的。其实啊，颜色的深度表示该像素利用了原始特征图上像素的次数。是不是不好理解呢，这里我详细的说一下。【这一部分推荐视频中也没有介绍的很清楚，下面几张图片都来自视频】

​   首先我们来看一下，经过第一次3×3的卷积，每个像素都只利用了原图上的一个像素，这很好理解，如下图：

​

​   接下来，经过第二次空洞卷积，得到的结果如下：

​   这次看着复杂多了，但其实你要明白了某个数字是怎么得到的，其它的都很简单了。我们来看上图最中间红色的9怎么得到的，如下图所示：

​   右图中的一个像素是由左图的9个像素得到，而左图9个像素都只对应原图上了一个像素，故右图红色点上数字为9。我们再以左上角的一个像素为例，如下：

​   上面右图中左上角的一个像素对应左图中9个像素，而这9个像素只有包含一个红色像素，故左上角的数字为1。介绍了这两个例子后，大家可以尝试其它的数值。

​   最后，经过第3次空洞卷积后，得到下图：

​   这里我就不带大家看了，通过上文的讲解，相信大家能自己解决了。

 

如何高效利用空洞卷积✨✨✨

​   既然空洞卷积存在着网格效应，那有什么方法可以解决这个问题吗。开门见山，论文中巧妙的使用了不同膨胀因子的空洞卷积，这样就能有效解决空洞卷积网格效应的问题，如下图所示：

​   是不是发现没有网格了呢，而且感受野大小也是一样的。这里在来看看使用这种方式在语义分割中的效果，如下图：

​   大家应该能很直观的感受到使用不同r的空洞卷积的效果要更好。

 

小结

​   关于空洞卷积的知识就为大家介绍到这里了，如若你还有不了解的地方，可以评论区咨询，希望我们一起进步。

 
 
如若文章对你有所帮助，那就

咻咻咻咻~~duang~~点个赞呗