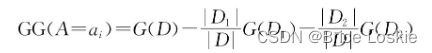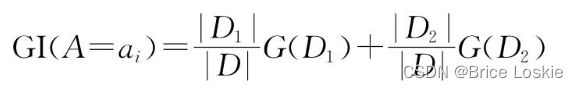基尼不纯度,基尼增益和基尼指数原理以及数学推导--CART决策树根据基尼增益的划分原理与计算过程详解
我们用jupyer种画出图如下
import matplotlib.pyplot as plt
x_1=[1,1,1,2,2.8]
y_1=[1,2,5,6,4]
plt.scatter(x_1,y_1,c='b')
x_2=[3,3,3,4,5]
y_2=[1,4,5,6,5]
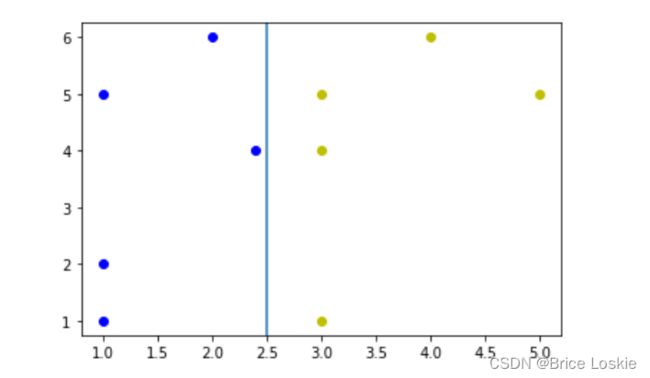
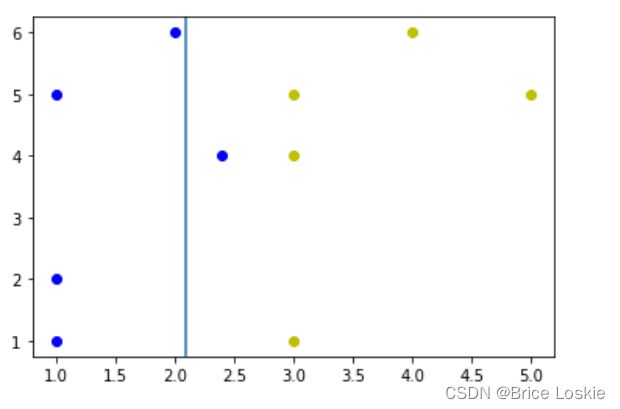
plt.scatter(x_2,y_2,c='y')我们现在需要找到一条曲线将它很好的分类
下图是将之很好分类的直线x=2.5
1.基尼不纯度
我们先来看一看什么是基尼不纯度:基尼不纯度是CART算法用来量化评估分割的好坏的方法。
我们先来看一下下图数据的基尼不纯度
带入公式 C=2,![]() =0.5,
=0.5,![]() =0.5 G计算如下
=0.5 G计算如下
0.5*0.5+0.5*0.5则此时的基尼不纯度为0.5
1.1 完美分割
当完美分割的时候我们在来计算此时的基尼不纯度
Gleft=1×(1-1)+0×(1-0)=0 Gright=0×(1-0)+1×(1-1)=0
则此时的基尼不纯度为0
1.2 不完美的分割
Gleft=0
按照权重来计算总的基尼不纯度G=0.4*Gleft+0.6*Gright=0.167
2.基尼增益和基尼指数
上面完美分割的基尼增益为0.5-0=0.5
不完美分割的基尼增益为0.5-0.167=0.333
对于一个样本数据集D,假设有属性A,它的取值为ai,i∈{1,2,…,n},初始的基尼不纯度为G(D)。则根据属性A的值ai进行划分时,形成两个子集合D1和D2,其中D1={v∈D|vA=ai},D2={v∈D|vA=ai},则基尼不纯度G(D1)和G(D2)分别根据子集合D1和D2里的样本情况进行计算。集合D、D1和D2中的样本数量分别用|D|、|D1|和|D2|表示,则根据属性A的值ai进行划分时,所获得的基尼增益的计算公式如下:
我们把会的基尼增益的公式归纳如下:
基尼指数是
3.CART分类决策树的原理
3.1 CART分类决策树的算法流程
3.1.1 输入
输入为训练数据集D和停止计算的条件。
其中,训练数据集D包含多条记录,每个记录由多个属性构成。每个属性的数据类型均为离散的,例如二值类型、标称值或枚举值类型等。
停止计算的条件可以是节点中的样本个数小于预定阈值,或样本集的基尼指数小于预定阈值,或没有更多特征属性等。
3.1.2 输出
输出为CART分类树。
3.1 3 CART分类决策树的生成流程
CART算法从根节点开始,用训练集递归地建立CART分类决策树。
1)设训练数据集为D,计算数据集现有的所有属性特征对该训练集的基尼增益。
2)在所有可能的属性特征中,选择基尼增益最大的特征及其对应的切分点作为最优切分点,依据该最优切分点切割,生成两个子节点,左子节点为D1,右子节点为D2。
3)对两个子节点递归调用步骤1~2,直至满足停止条件。
4)生成一棵完整的二叉CART分类决策树。
3.1.4 CART分类决策树的优化
使用决策树模型拟合数据时容易产生过拟合,解决办法是对决策树进行剪枝处理。决策树剪枝有两种思路:预剪枝(pre-pruning)和后剪枝(post-pruning)。我们将在之后提到
3.1.5 CART分类决策树模型的使用
对生成的CART分类决策树做预测的时候,如果测试集里的某个样本A落到了某个叶子节点,且该叶子节点里存在多个类别的训练样本,则概率最大的训练样本是样本A的类别。
3.2 CART分类决策树的生成实例
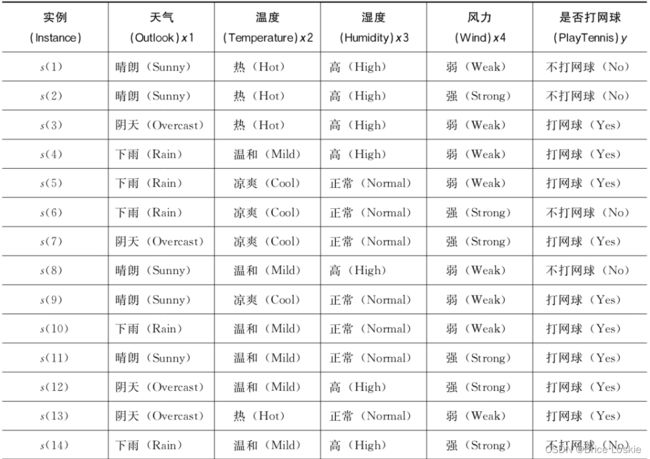
如下是一个是否打网球的数据集 我们将对之生成CART决策树
原始数据分析共14个数据,其中9个打网球 5个不大网球
所以原始数据的基尼不纯度为
G=1-(9/14)2-(5/14)2≈1-0.413-0.128=0.459
当我们考虑第一个属性特征天气时
| 属性特征(天气) | 打球 | 不打球 | 样本数量 |
| 晴天 | 2 | 3 | 5 |
| 阴天 | 4 | 0 | 4 |
| 下雨 | 3 | 2 | 5 |
G(天气=晴天)=
=0.48
G(天气≠晴天)=
=0.34
G(天气=阴天)=0
G(天气≠阴天)=0.5
G(天气=下雨)=0.48
G(天气≠下雨)=0.45
GG(天气=晴天)=G-5/14*G(天气=晴天)-9/14*G(天气≠晴天)=0.069
GI(天气的晴天)=(5/14)*0.48+(9/14)*0.34=0.39
GG(天气=阴天)=G-(4/14)*0-(10/14)*0.5=0.102
GI(天气≠阴天)=0.357
GG(天气=下雨)=G-(5/14)*0.48-(9/14)*0.45=0
GI(天气=下雨)=0.46
当我们考虑第二个特征温度时
| 属性特征(温度) | 打球 | 不打球 | 样本数量 |
| 热 | 2 | 2 | 4 |
| 温和 | 4 | 2 | 6 |
| 凉爽 | 3 | 1 | 4 |
G(温度=热)=0.5
G(温度≠热)=1-(7/10)^2-(3/10)^2=0.42
G(温度=温和)=
=0.445
G(温度≠温和)=0.445
G(温度=凉爽)=0.375
G(温度≠凉爽)=0.48
CG(温度=热)=0.016
GI(温度=热)=0.443
CG(温度=温和)=0.014
GI((温度=温和)=0.445
CG(温度=凉爽)=0.009
GI((温度=凉爽)=0.45
当我们考虑第三个特征湿度时
| 属性特征(湿度) | 打球 | 不打球 | 样本数量 |
| 高 | 3 | 4 | 7 |
| 正常 | 6 | 1 | 7 |
考虑到之后我们会算很多基尼不纯度,基尼增益和基尼指数,这里我们将编写它们的代码方便之后的计算方便:
输入:将如上的表格按照ndarray数组输入和上一层的基尼指数
输出:输出每个特征的基尼不纯度,基尼增益和基尼指数
def G_calulation(nums,G_last):
G=np.zeros([nums.shape[0]])
for i in range(nums.shape[0]):
G[i]=1-(nums[i,0]/nums[i,2])**2-(nums[i,1]/nums[i,2])**2
sum_1=0
sum_2=0
sum_3=0
for i in range(nums.shape[0]):
sum_1=nums[i,0]+sum_1
sum_2=nums[i,1]+sum_2
sum_3=nums[i,2]+sum_3
S=np.zeros([nums.shape[0]])
for i in range(nums.shape[0]):
S[i]=1-((sum_1-nums[i,0])/(sum_3-nums[i,2]))**2-((sum_2-nums[i,1])/(sum_3-nums[i,2]))**2
GI=np.zeros([nums.shape[0]])
GG=np.zeros([nums.shape[0]])
for i in range(nums.shape[0]):
GI[i]=(nums[i,2]/sum_3)*G[i]+(1-(nums[i,2]/sum_3))*S[i]
GG[i]=G_last-GI[i]
return G,S,GI,GG将表格转化成np数组
input=np.array([[3,4,7],[6,1,7]])结果如下
G_calulation(input,0.459)(array([0.48979592, 0.24489796]), array([0.24489796, 0.48979592]), array([0.36734694, 0.36734694]), array([0.09165306, 0.09165306]))
G(湿度=高)=0.48979592
G(湿度≠高)=0.24489796
G(湿度=正常)=0.24489796
G(湿度≠正常)=0.48979592
GI(湿度=高)=0.36734694
GI(湿度=正常)=0.36734694
GG(湿度=高)=0.09165306
GG(湿度=正常)=0.09165306
我们再考虑最后一个特征风力的影响
先制作表格如下
| 属性特征(风力) | 打球 | 不打球 | 样本数量 |
| 弱 | 6 | 2 | 8 |
| 强 | 3 | 3 | 6 |
制作成np数组然后带入写好的函数得到如下结果
(array([0.375, 0.5 ]), array([0.5 , 0.375]), array([0.42857143, 0.42857143]), array([0.03042857, 0.03042857]))
G(湿度=弱)=0.375
G(湿度≠弱)=0.5
G(湿度=强)=0.5
G(湿度≠强)=0.375
GI(湿度=弱)=0.42857143
GI(湿度=强)=0.42857143
GG(湿度=弱)=0.03042857
GG(湿度=强)=0.03042857
我们现在需要把所有的基尼增益列出来进行比较
GG(天气=晴天)=0.069
GG(天气=阴天)=0.102
GG(天气=下雨)=0
CG(温度=热)=0.016
CG(温度=温和)=0.014
CG(温度=凉爽)=0.009
GG(湿度=高)=0.09165306
GG(湿度=正常)=0.09165306
GG(湿度=弱)=0.03042857
GG(湿度=强)=0.03042857
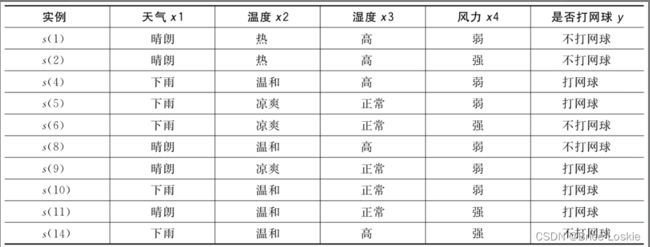
用天气=阴天进行第一次划分
划分后整个数据集被分成D1和D2
如下表所示
考虑子集D1,由于该子集中所有样本都是打网球,因此,该子集直接生成叶子节点。
对于子集D2,可以继续上述过程,选择合适的属性特征及其分割点,生成后续的子节点。
G=1-(5/10)**2-(5/10)**2=0.5
考虑天气情况得到如下表
| 属性特征(天气) | 打球 | 不打球 | 样本数量 |
| 晴朗 | 2 | 3 | 5 |
| 下雨 | 3 | 2 | 5 |
考虑温度情况得到如下表
| 属性特征(温度) | 打球 | 不打球 | 样本数量 |
| 热 | 0 | 2 | 2 |
| 温和 | 3 | 2 | 5 |
| 凉爽 | 2 | 1 | 3 |
考虑湿度情况得到如下表
| 属性特征(湿度) | 打球 | 不打球 | 样本数量 |
| 高 | 1 | 4 | 5 |
| 正常 | 4 | 1 | 5 |
考虑风力情况得到如下表
| 属性特征(天气) | 打球 | 不打球 | 样本数量 |
| 弱 | 4 | 2 | 6 |
| 强 | 1 | 3 | 4 |
带入函数得到如下结果
(array([0.48, 0.48]), array([0.48, 0.48]), array([0.48, 0.48]), array([0.02, 0.02]))(array([0. , 0.48 , 0.44444444]), array([0.46875 , 0.48 , 0.48979592]), array([0.375 , 0.48 , 0.47619048]), array([0.125 , 0.02 , 0.02380952]))(array([0.32, 0.32]), array([0.32, 0.32]), array([0.32, 0.32]), array([0.18, 0.18]))(array([0.44444444, 0.375 ]), array([0.375 , 0.44444444]), array([0.41666667, 0.41666667]), array([0.08333333, 0.08333333]))
GG(天气=晴朗)=0.02
GG(天气=下雨)=0.02
CG(温度=热)=0.125
CG(温度=温和)=0.02
CG(温度=凉爽)=0.02380952
GG(湿度=高)=0.18
GG(湿度=正常)=0.18
GG(湿度=弱)=0.08333333
GG(湿度=强)=0.08333333
第二次划分通过湿度=高和湿度=正常都可以
我们这里选取湿度等于正常来划分
得到数据集D1和数据集D2
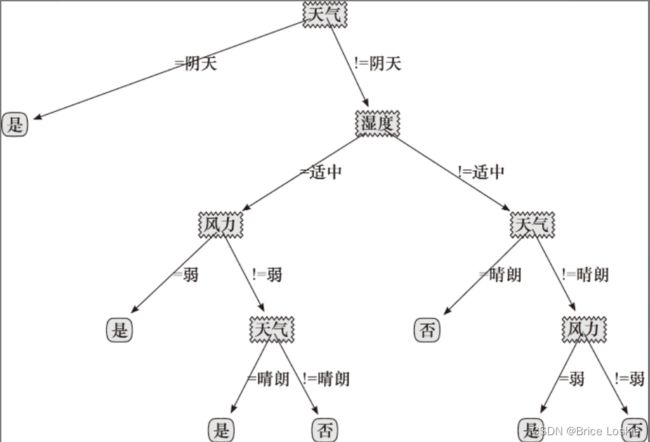
通过如上所示的方法,对之进行又一次的循环
最后进行得到决策树的结果如下