基于强化学习的空域作战辅助决策(1D)
基于强化学习的空域作战辅助决策
1.1-D Problem
1.1 问题描述
简化的一维问题由3部分组成:战斗机、干扰机和地对空导弹系统(SAM)构成。战斗机的目标是摧毁防御系统SAM,SAM的主要目的是摧毁战斗机。在这篇构想中,SAM在射程上占据优势(100KM),其中战斗机的射程只有80KM。因此SAM可以在战斗机靠近之前用地空导弹摧毁战斗机。
然而,时机和位置是很重要的。如果额外添加一个干扰机,这将从增加结果可能性的角度增加战斗机的部分优势。干扰机可以靠近SAM并且减少SAM的射程。如果战斗机在此时进入,其便可以摧毁SAM并且生存下来。但是,干扰机也可能在战斗机摧毁SAM之前被摧毁,最终导致二者皆被击落。机器学习(强化学习)的算法将以SAM的位置,以战斗机、干扰机和SAM的射程为输入,在保证没有任一个飞机损失的情况下,得到在什么时刻以及什么位置投放战斗机以及干扰机能摧毁SAM系统。实际情况下的任务规划是在标准的3维环境下,然而决策变量却是一维的(比如前进或者后退)。下表表明了一些战斗机,干扰机以及SAM的属性:
该场景是一维的,因为所有飞机都被约束在连接蓝色和红色起始位置的同一条线上飞行。蓝方飞机的高度保持不变。为确保能给我们的AI系统提供足够多样的经验用来学习,红方SAM的位置选择为从给定初始位置偏离一个随机的距离。我们的AI系统重点学习以下知识:
-
1.在战斗机出发之前投送干扰机,保证其使得SAM失效
-
2.将干扰机与SAM保持一定距离,要足够近保证有效,但不能太近使得有被击落的风险
-
3.排出战斗机攻击SAM,但不要靠的太近
-
4.战斗机与干扰机都成功返回基地
如下图所示的一个例子表明,蓝色战斗机跟踪成功干扰红色地对空导弹系统SAM的干扰机(这个动作可以通过橙色干扰线看出,事实上黄色探测线只从蓝色平台流向地对空导弹)。这个特殊的例子继续展示了战斗机成功地飞入,射击萨姆导弹,并转身。
1.2 数据来源
每组场景都由两组变量定义:环境与学习。第一组变量包括预先确定的场景特征,设置一个初始的世界状态。例如火力范围是一个环境变量,设置它的值帮助定义机器学习的工作环境。第二组变量是学习变量,其代表了机器学习代理特征,设置这个值用来描述描述其与环境交互的任务规划或者路径规划。例如,平台飞行的距离可以是一个学习变量,并且可能取决于环境中的特征,例如附近平台的射程。在一维的平台任务规划问题中,机器学习代理寻找能给定条件下的最优方案。下表描述了平台的行为和场景的变量:
如果改变射程与距离变量的范围再学习,那样就能教会战斗机一个通用的策略(与距离和射程无关),而不是去学习一个只和一个具体场景有关的策略。在这里不考虑任何碰撞操作。
人工智能系统对抗性学习的训练数据由大约20000个随机生成的各自的计划对组成。因此,对于训练数据,提供了环境和学习值。环境变量值是在表2.2给出的范围内随机选择的,给定一个环境变量,其值在下表的范围内随机生成:
1.3 1-D问题的环境搭建
1.3.1 状态转移方程
设 t t t时刻战斗机的位置为 x F ( t ) x_{F}^{(t)} xF(t),干扰机的位置为 x J ( t ) x_J^{(t)} xJ(t)。而SAM系统与战斗机,干扰机之间的初始位置之间的距离为 L L L,时间步长为 Δ t \Delta t Δt,战斗机与无人机的速度分别为 v F , v J v_F,v_J vF,vJ,干扰机前进距离(Jammer Lead Distance)的 d d d,战斗机、干扰机、SAM的射程 R F , R J , R S A M R_F,R_J,R_{SAM} RF,RJ,RSAM,SAM导弹的锁定时间为 t 0 t_0 t0。
战斗机与干扰机的时序方程如下:
( x F ( t + 1 ) x J ( t + 1 ) ) = ( x F ( t ) x J ( t ) ) + ( a F ( t ) , 0 0 , a J ( t ) ) ( v F v J ) Δ t \begin{pmatrix} x_F^{(t+1)}\\x_J^{(t+1)} \end{pmatrix}=\begin{pmatrix} x_F^{(t)}\\x_J^{(t)} \end{pmatrix}+\begin{pmatrix} a_F^{(t)},0\\0,a_J^{(t)} \end{pmatrix}\begin{pmatrix} v_F\\v_J \end{pmatrix}\Delta t (xF(t+1)xJ(t+1))=(xF(t)xJ(t))+(aF(t),00,aJ(t))(vFvJ)Δt
其中 a F ( t ) , a J ( t ) a_F^{(t)},a_J^{(t)} aF(t),aJ(t)为动作变量,当 a ∗ ( t ) = 1 a_*^{(t)}=1 a∗(t)=1时战斗机/干扰机继续向前;当 a ∗ ( t ) = 0 a_*^{(t)}=0 a∗(t)=0时战斗机/干扰机停留在原地;当 a ∗ ( t ) = − 1 a_*^{(t)}=-1 a∗(t)=−1时战斗机/干扰机朝相反方向运动。在此设状态 s t = ( x F ( t ) , x J ( t ) ) T ∈ [ 0 , L ] × [ 0 , L ] s_t=\begin{pmatrix}x_F^{(t)},x_J^{(t)} \end{pmatrix}^T\in[0,L]\times[0,L] st=(xF(t),xJ(t))T∈[0,L]×[0,L],初始状态 s 0 = ( 0 , d ) T s_0=(0,d)^T s0=(0,d)T。动作 a t = ( a F ( t ) , a J ( t ) ) T ∈ { − 1 , 0 , 1 } × { − 1 , 0 , 1 } a_t=(a_F^{(t)},a_J^{(t)})^T\in\{-1,0,1\} \times \{-1,0,1\} at=(aF(t),aJ(t))T∈{−1,0,1}×{−1,0,1}。
1.3.2 奖励函数
设第 t t t时刻战斗机、干扰机与SAM系统的距离为 d F ( t ) , d J ( t ) d_{F}^{(t)},d_J^{(t)} dF(t),dJ(t)。其中: d ∗ ( t ) = L − x ∗ ( t ) d^{(t)}_*=L-x^{(t)}_* d∗(t)=L−x∗(t)。其奖励满足以下设定:
-
对干扰机而言其位置在战斗机之前: x J ( t ) ≥ x F ( t ) x_J^{(t)}\geq x_F^{(t)} xJ(t)≥xF(t)。如果满足要求奖励返回-1,否则返回-50,并结束回合。
-
对于干扰机与战斗机如果其均在SAM射程之外即: d J ( t ) > R S A M ⋂ d F ( t ) > R S A M d_{J}^{(t)}>R_{SAM}\bigcap d_{F}^{(t)}>R_{SAM} dJ(t)>RSAM⋂dF(t)>RSAM,则其能保证安全,其奖励为-1,回合继续。
-
如果SAM系统能正常工作,且干扰机在SAM的射程中的存在时间长于导弹瞄准时间 t 0 t_0 t0,那么导弹将瞄准干扰机,瞄准后就将击落。即: d J ( t ) ≤ R S A M ⋂ t J a m m e r ≥ t 0 ⋂ E n a b l e S A M = = 1 d_{J}^{(t)}\leq R_{SAM} \bigcap t_{Jammer}\geq t_0\bigcap Enable_{SAM}==1 dJ(t)≤RSAM⋂tJammer≥t0⋂EnableSAM==1,此时返回奖励-100,同时 t J a m m e r = 0 t_{Jammer}=0 tJammer=0。并且结束回合。
-
如果SAM系统能正常工作,且干扰机在SAM的射程中的存在时间短于导弹瞄准时间 t 0 t_0 t0,那么导弹将持续锁定干扰机。即 d J ( t ) ≤ R S A M ⋂ t J a m m e r < t 0 ⋂ E n a b l e S A M = = 1 d_{J}^{(t)}\leq R_{SAM}\bigcap t_{Jammer}< t_0 \bigcap Enable_{SAM}==1 dJ(t)≤RSAM⋂tJammer<t0⋂EnableSAM==1,此时返回奖励-1,同时 t J a m m e r ← t J a m m e r + Δ t t_{Jammer} \leftarrow t_{Jammer}+\Delta t tJammer←tJammer+Δt。并且回合继续。
-
如果SAM系统能正常工作,且战斗机出现在SAM的射程以内,其规则同干扰机类似。
-
如果SAM系统在干扰机的射程以内 d J ( t ) ≤ R J d_{J}^{(t)}\leq R_J dJ(t)≤RJ,不考虑干扰机的作用时长,此时SAM系统将受到一定程度的干扰 E n a b l e S A M = 0 Enable_{SAM}=0 EnableSAM=0。
-
如果SAM系统受到了干扰 E n a b l e S A M = 0 Enable_{SAM}=0 EnableSAM=0,那么对于SAM系统对于干扰机与战斗机出现在其射程内时,均只有一定的概率 p p p将其击落。
-
如果SAM系统在战斗机的射程之内 d F ( t ) ≤ R F d_F^{(t)}\leq R_{F} dF(t)≤RF,且战斗机未被击落,那么SAM系统将会受到战斗机的致命打击,此时返回奖励+100,回合结束。
搭建的环境代码如下:
class SAMenv(object): def __init__(self,L=100,Delta_t=10,t0=15,tJ=3,v_F=740.0/3600,v_J=740.0/3600,R_F=40,R_J=30,R_SAM=40,P_disable=0.5): self.L = L self.Delta_t = Delta_t self.tJ = tJ self.v_F = v_F self.v_J = v_J self.R_F = R_F self.R_J = R_J self.R_SAM = R_SAM self.t0 = t0 self.P_disable = P_disable self.Jammer_time = 0 self.Fighter_time = 0 self.SAM_disable = 0 self.observation_space_num = 2 self.action_space_num = 9 self.Jammer_wait_time = 0 # 与tJ对应,干扰机的发射时间 self.a_F = 0 self.a_J = 0 self.state = np.array([0,np.random.random()*L]) def reset(self): self.state = np.array([0,np.random.random()*self.L]) self.SAM_disable = 0 self.Jammer_time = 0 self.Fighter_time = 0 self.Jammer_wait_time = 0 return self.state def step(self,action): # action;0-8的二维化,类型为int a_F = int(action)//3 - 1 a_J = int(action)%3 - 1 # 储存当前动作 self.a_F = a_F self.a_J = a_J # 当前的状态变量 x_F = self.state[0] x_J = self.state[1] # 下一个时刻的状态变量 x_F_ = x_F + a_F*self.v_F*self.Delta_t x_J_ = x_J + a_J*self.v_J*self.Delta_t # 限制战斗机在一定区域内飞行 if x_F_ >= self.L: x_F_ = self.L if x_F_ <= 0: x_F_ = 0 # 限制干扰机在一定区域内飞行 if x_J_ >= self.L: x_J_ = self.L if x_J_ <=0: x_J_ = 0 # 对下个状态进行赋值 self.state = np.array([x_F_,x_J_]) # 当前的战斗机与干扰机与SAM的距离 d_F_ = self.L - x_F_ d_J_ = self.L - x_J_ # 如果干扰机与战斗机均在SAM射程之外,则返回-1 if d_J_ >= self.R_SAM and d_F_ >= self.R_SAM: return self.state,-1,False # 如果干扰机/战斗机持续在射程内则更新瞄准时间 if d_J_ <= self.R_SAM and self.Jammer_time < self.t0: self.Jammer_time += self.Delta_t if d_F_ <= self.R_SAM and self.Fighter_time < self.t0: self.Fighter_time += self.Delta_t # 如果干扰机/战斗机超过射程则重新记录时间 if d_J_ > self.R_SAM: self.Jammer_time = 0 if d_J_ > self.R_J: self.Jammer_time = 0 if d_F_ > self.R_SAM: self.Fighter_time = 0 if d_J_ <= self.R_J: self.Jammer_wait_time += self.Delta_t # 若干扰机的干扰对SAM系统起了作用 if self.Jammer_wait_time >= self.tJ: self.SAM_disable = 1 # 如果SAM系统能正常工作 if self.SAM_disable == 0: # 瞄准时间已到 if d_J_ <= self.R_SAM and self.Jammer_time >= self.t0: self.Jammer_time = 0 #击毁之后重新记录时间 self.Jammer_wait_time = 0 return self.state,-100,True if d_F_ <= self.R_SAM and self.Fighter_time >= self.t0: self.Fighter_time = 0 return self.state,-100,True # 如果SAM系统被麻痹 if self.SAM_disable == 1: #将依照一定的概率执行瞄准与击毁操作 if np.random.random() >= (1 - self.P_disable): if d_J_ <= self.R_SAM and self.Jammer_time >= self.t0: self.Jammer_time = 0 #击毁之后重新记录时间 self.Jammer_wait_time = 0 return self.state,-100,True if d_F_ <= self.R_SAM and self.Fighter_time >= self.t0: self.Fighter_time = 0 return self.state,-100,True # 如果SAM系统在战斗机射程以内且战斗机未被击落,战斗机将对SAM系统产生致命打击 if d_F_ <= self.R_F: return self.state,1000,True # 如果以上情况都没执行,则正常返回 return self.state,-1,False下面是测试代码:
env = SAMenv(L=100,Delta_t=10.0/3600,t0=3/60,tJ=3/60,v_F=740.0,v_J=740.0,R_F=40,R_J=30,R_SAM=40,P_disable=0.9) # delta_t:10s for epoch in range(10): print("----第{}论迭代------".format(epoch)) state = env.reset() print("初始状态为{}".format(state)) done = False rewards = 0 while done == False: action = np.random.randint(0,9) new_state,r,done = env.step(action) rewards += r # print("在接受动作A_F:{},A_J:{}后".format(env.a_F,env.a_J)) # print("新状态为{}".format(new_state)) print("终止状态为{}".format(new_state)) print("----第{}论迭代的奖励是{}------".format(epoch,rewards))结果如下:
1.4 1-D问题的求解
用PPO求解:
# 下面是定义环境
env = SAMenv(L=100,Delta_t=10.0/3600,t0=3/60,tJ=3/60,v_F=740.0,v_J=740.0,R_F=40,R_J=30,R_SAM=40,P_disable=0.9)
# 下面是定义参数阶段
ppo_net = PPO(num_inputs=2,num_outputs=9,num_hiddens=64,lr=0.002)
epsiode_rewards,mean_rewards = ppo_net.train_network(env,epsiodes=300)
# 下面开始画图
plt.plot(epsiode_rewards)
plt.plot(mean_rewards)
plt.xlabel('epsiode')
plt.ylabel('rewards')
plt.title(str(epsiode_rewards[-1]))
结果测试:
# 下面进行测试
x,y,rewards = [],[],0
state = env.reset()
while True:
x.append(state[0])
y.append(state[1])
action,_ = ppo_net.policy.select_action(state)
state,r,done = env.step(action)
rewards += r
if done:
print("奖励为{}".format(rewards))
break
plt.plot(x)
plt.plot(y)
plt.xlabel("time/10s")
plt.ylabel("location/km")
plt.title("PPO_solve rewards:{}".format(rewards))
plt.legend(['Fighter','Jammer'])
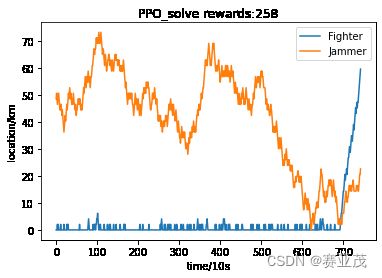
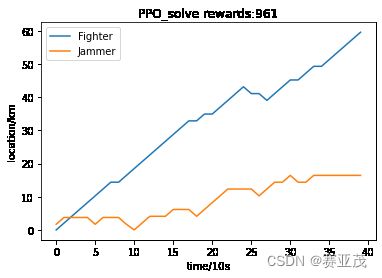
几种比较优势的结果:
其最优求得的一组结果为:(rewards=961,可以说是奇兵奇策了!)
由图可知最好的策略应当是战斗机与干扰机距离尽可能接近的时候直接采用战斗机突袭后返回。
1.5 PPO调用代码
# 下面将定义一个演员价值类
class ActorCritic(nn.Module):
def __init__(self,num_states,num_actions,num_hiddens=64,lr=0.01):
super(ActorCritic,self).__init__()
self.action_layers = nn.Sequential(
nn.Linear(num_states,num_hiddens),
nn.Tanh(),
nn.Linear(num_hiddens,num_actions),
nn.Tanh(),
nn.Softmax()
)
self.value_layers = nn.Sequential(
nn.Linear(num_states,num_hiddens),
nn.Tanh(),
nn.Linear(num_hiddens,1)
)
self.optimizer = torch.optim.Adam(self.parameters(),lr=lr)
def forward(self,state):
# 输入的state是numpy类型
pass
def select_action(self,state):
# 输入state是numpy类型
state = torch.from_numpy(state).float()
dist = self.action_layers(state)
#values = self.value_layers(state)
categorical = Categorical(dist)
action = categorical.sample()
log_prob = categorical.log_prob(action)
return action.item(),log_prob
# 评估lnpi(a|s),v(s)
def evaluate_action(self,state,action):
# 其中state是torch类型
# action是int类型
#state = torch.from_numpy(state).float()
# action = torch.tensor(action)
dist = self.action_layers(state)
values = self.value_layers(state)
action_probs = Categorical(dist).log_prob(action)
return action_probs,torch.squeeze(values)
# 下面将定义PPO算法的框架
class PPO(object):
def __init__(self,num_inputs=2,num_outputs=3,num_hiddens=64,epsilon=0.2,gamma=0.9,K_epochs=4,lr=0.01):
# 存储参数
self.gamma = gamma
self.epsilon = epsilon
# 定义一个老的参数policy网络与一个新的policy网络
self.policy = ActorCritic(num_states=num_inputs,num_actions=num_outputs,num_hiddens=num_hiddens,lr=lr)
self.policy_old = ActorCritic(num_states=num_inputs,num_actions=num_outputs,num_hiddens=num_hiddens,lr=lr)
self.policy_old.load_state_dict(self.policy.state_dict()) # 将theta_old 的初值考虑为与theta一样
# 误差项
self.mesLoss = nn.MSELoss()
self.k_epochs = K_epochs
self.optimizer = torch.optim.Adam(self.policy.parameters(),lr=lr)
self.losses = []
# 下面定义储存状态的数组
self.saved_states = []
self.saved_rewards = []
self.saved_log_probs = []
# self.saved_state_values = []
self.saved_actions = []
self.saved_is_done = []
# 策略更新(实际上是在更新网络参数)
def update_policy(self):
# 由存储的数组中的数据计算Gt(累计折扣回报)
discounted_rewards = []
G = 0
for reward,is_done in zip(reversed(self.saved_rewards),reversed(self.saved_is_done)):
if is_done:
G = 0
G = reward + G*self.gamma
discounted_rewards.insert(0,G)
# 折扣回报标准化
discounted_rewards = torch.tensor(discounted_rewards)
discounted_rewards = (discounted_rewards - torch.mean(discounted_rewards))/torch.std(discounted_rewards)
## 下面明天继续写先打骑砍了....
old_states = torch.tensor(self.saved_states).float()
old_actions = torch.tensor(self.saved_actions)
old_logprobs = torch.tensor(self.saved_log_probs)
# 优化策略
for _ in range(self.k_epochs):
logprobs,state_values = self.policy.evaluate_action(old_states,old_actions) #返回的应该是一个数组
#找到比率
ratio = torch.exp(logprobs - old_logprobs)
# 计算优势函数
advatange = discounted_rewards - state_values
surr1 = ratio*advatange
surr2 = torch.clamp(ratio,1-self.epsilon,1+self.epsilon)*advatange
loss = -torch.min(surr1,surr2) + 0.5*self.mesLoss(state_values,discounted_rewards)
self.losses.append(loss.mean()) # 用大数定理,均值逼近期望
# 采取梯度措施
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
# 将新的参数赋值到原来的网络theta_old中
self.policy_old.load_state_dict(self.policy.state_dict())
# 训练网络
def train_network(self,env,epsiodes=100):
epsiode_rewards = []
mean_rewards = []
for epsiode in range(epsiodes):
state = env.reset()
epsiode_reward = 0
while True:
action,log_prob = self.policy_old.select_action(state)
next_state,reward,done = env.step(action)
# 保存各个回报与参数
self.saved_log_probs.append(log_prob)
self.saved_states.append(state)
self.saved_actions.append(action)
self.saved_rewards.append(reward)
self.saved_is_done.append(done)
epsiode_reward += reward
# 状态转换
state = next_state
if done:
# 因为是MonteCarlo估计则每个轨迹结束后更新策略
self.update_policy()
self.clean()
break
epsiode_rewards.append(epsiode_reward)
mean_rewards.append(np.mean(epsiode_rewards[-10:]))
print("第{}回合的奖励值是{:.2f},平均奖励是{:.2f}".format(epsiode,epsiode_reward,mean_rewards[-1]))
return epsiode_rewards,mean_rewards
# 清空数组
def clean(self):
del self.saved_states[:]
del self.saved_actions[:]
del self.saved_rewards[:]
del self.saved_log_probs[:]
del self.saved_is_done[:]