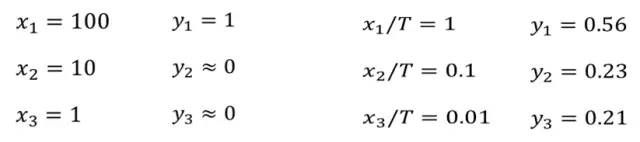模型压缩|深度学习(李宏毅)(十三)
一、概述
需要做模型压缩的原因在于我们有将模型部署在资源受限的设备上的需求,比如很多移动设备,在这些设备上有受限的存储空间和受限的计算能力。本文主要介绍五种模型压缩的方法:
①网络剪枝(Network Pruning)
②知识蒸馏(Knowledge Distillation)
③参数量化(Parameter Quantization)
④结构设计(Architecture Design)
⑤动态计算(Dynamic Computation)
二、网络剪枝(Network Pruning)
网络剪枝的步骤
神经网络中的一些权重和神经元是可以被剪枝的,这是因为这些权重可能为零或者神经元的输出大多数时候为零,表明这些权重或神经元是冗余的。
网络剪枝的过程主要分以下几步:
①训练网络;
②评估权重和神经元的重要性:可以用L1、L2来评估权重的重要性,用不是0的次数来衡量神经元的重要性;
③对权重或者神经元的重要性进行排序然后移除不重要的权重或神经元;
④移除部分权重或者神经元后网络的准确率会受到一些损伤,因此我们要进行微调,也就是使用原来的训练数据更新一下参数,往往就可以复原回来;
⑤为了不会使剪枝造成模型效果的过大损伤,我们每次都不会一次性剪掉太多的权重或神经元,因此这个过程需要迭代,也就是说剪枝且微调一次后如果剪枝后的模型大小还不令人满意就回到步骤后迭代上述过程直到满意为止。
为什么可以进行网络剪枝
在实践过程中我们可以感受到大的网络比小的网络更容易训练,而且也有越来越多的实验证明大的网络比小的网络更容易收敛到全局最优点而不会遇到局部最优点和鞍点的问题。解释这一想象的一个假设是大乐透假设(Lottery Ticket Hypothesis)。
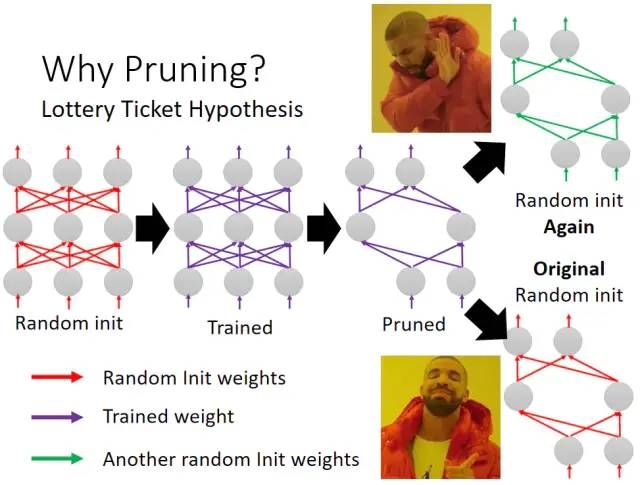
Lottery Ticket Hypothesis
Reference:https://arxiv.org/abs/1803.03635
在下图中,首先我们使用一个大的网络然后随机初始化一组参数,这组参数用红色表示,然后训练后得到紫色的参数,接着进行网络剪枝。我们再尝试使用剪枝的网络结构随机初始化一组参数然后训练发现这种方式没能取得剪枝得到的效果,而如果用大的网络中对应的初始化参数来初始化这个剪枝的网络结构然后再进行训练,就发现可以取得较好的效果:
大乐透假设可以用来解释这个现象,在买大乐透时买得越多就越容易中奖,同样的这里我们假设一个大的网络中包含很多小的网络,这些小的网络结构有的可以训练成功而有的不可以训练成功,只要有一个训练成功,整个大的网络结构就可以训练成功,因此我们可以把多余的网络结构剪枝掉。
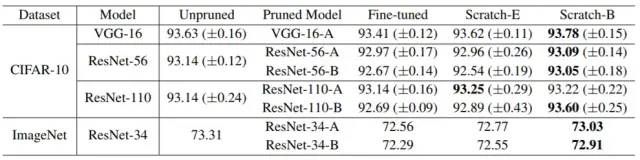
Rethinking the Value of Network Pruning
Reference:https://arxiv.org/abs/1810.05270
与大乐透假设不同的是《Rethinking the Value of Network Pruning》这篇得出了与其看似矛盾的假设。在下表中的实验中使用了不同的模型进行试验,表中Fined-tuned表示剪枝后的模型,Scratch-E和Scratch-B表示随机初始化剪枝网络的参数后训练的模型,只是Scratch-B训练了更多的epoch。可以看到随机初始化剪枝网络的参数后训练的模型也取得了不错的效果,这样就看起来和大乐透假设的实验结果相矛盾。事实上两篇paper的作者均对这种结果进行了回应,可以在网上找到回应的内容,这里不做赘述。
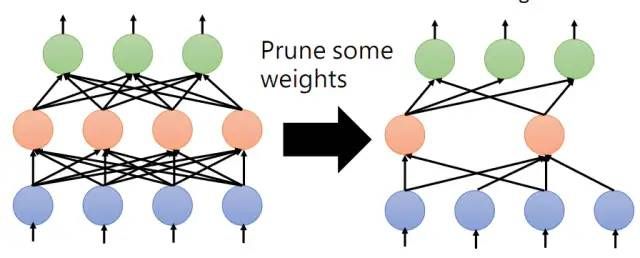
剪枝权重还是剪枝神经元
在进行网络剪枝时我们可以选择剪枝权重或者剪枝神经元。下图中进行了权重的剪枝:
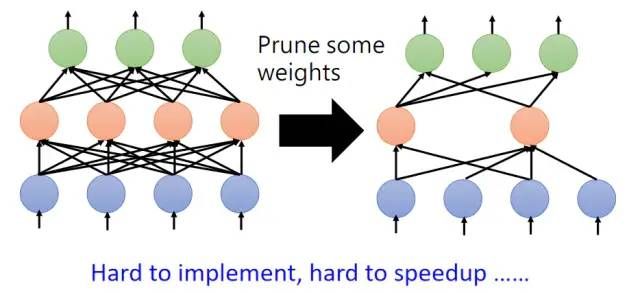
剪枝权重的问题是会造成网络结构的不规则,在实际操作中很难去实现也很难用GPU去加速。
下图展示了对AlexNet进行weight pruning后使用不同的GPU加速的效果,折线表示了对每一层的权重的剪枝的比例,被剪掉的权重大约占比95%左右,然后使用不同GPU加速发现加速效果并不好,这是因为剪枝做成了网络结构的不规则,因此难以用GPU进行加速。
在进行实验需要使用weight pruning时可以使用将被剪枝的权重设置成0的方法。
而使用Neuron pruning就不会遇到上述问题,Neuron pruning后的网络结构仍然是规则的,因此仍然可以使用GPU进行加速。
三、知识蒸馏(Knowledge Distillation)
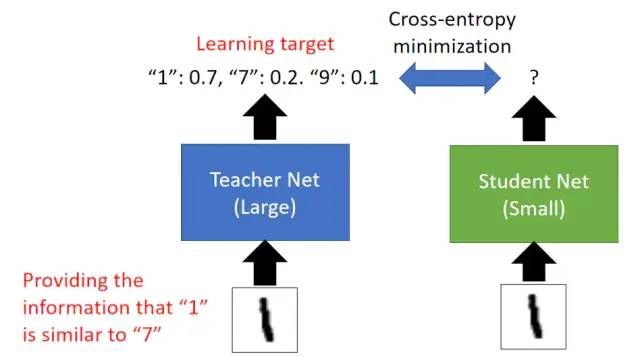
知识蒸馏的方式就是将Teacher Network输出的soft label作为标签来训练Student Network。比如在上图中我们训练Student Network来使其与Teacher Network有同样的输出。这样的好处是Teacher Network的输出提供了比独热编码标签更多的信息,比如对于输入的数字1,Teacher Network的输出表明这个数字是1,同时也表明了这个数字也有一点像7,也有一点像9。另外训练Student Network时通常使用交叉熵作为损失函数,这是因为训练过程相当于要拟合两个概率分布。
知识蒸馏训练出的Student Network有一点神奇的地方就是这个Network有可能辨识从来没有见过的输入,不如把Student Network的训练资料中的数字7移除后可能训练完成后也会认识数字7,这是因为Teacher Network输出的soft label提供了额外的信息。
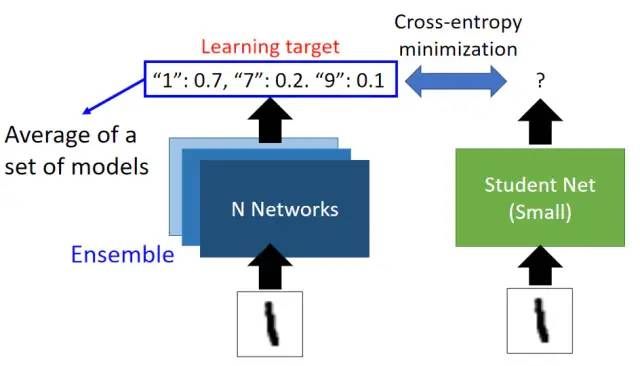
知识蒸馏的一个用处是用来拟合集成模型,有时候我们会集成(Ensemble)很多个模型来获取其输出的均值从而提高总体的效果,我们可以使用知识蒸馏的方式来使得
Student Network学习集成模型的输出,从而达到将集成模型的效果复制到一个模型上的目的:
在进行知识蒸馏时我们还会使用到下面的技巧就是调整最终输出的sofmax层来避免Teacher Network输出类似独热编码的标签:
通过下列数据的对比我们可以看出这一操作的作用:
在实际操作时是一个可以调的参数。
四、参数量化(Parameter Quantization)
使用更少的bits来表示一个参数,比如将64位浮点数换成32位浮点数。
权重聚类(Weight Clustering)
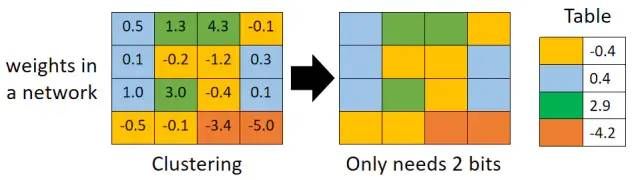
下图方格代表权重,我们可以使用聚类算法(如K-Means)来将权重进行聚类,然后每个权重就只需要存储对应的类别,比如下图中聚成了四类则每个权重只需要2个bit就可以存储,另外还需要存储四类的值,每个值都是该类中所有参数的平均值:
用更少的bit表示频繁出现的类别,用较多的bit来表示出现较少的类别。例如使用哈弗曼编码(Huffman encoding)。
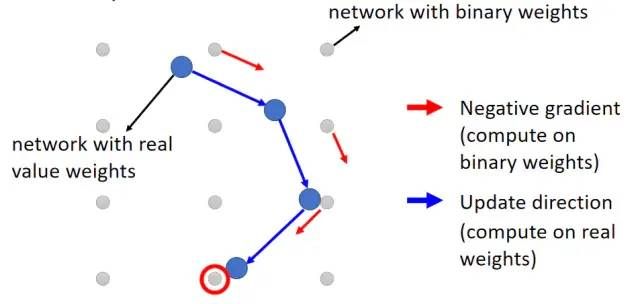
使用二进制参数(Binary Weights),使用Binary Connect的方式训练神经网络,下图代表参数空间,灰色点代表二进制的一组参数,更新梯度时计算离当前参数最近的二进制参数的梯度然后进行梯度下降,最终的结果也是取距离最近的一组二进制参数:
下图中展示了使用Binary Connect的一组实验结果,可以看到使用Binary Connect的方式可以取得比无正则化更好的效果,这是因为使用Binary Connect相当于做了正则化操作:
五、结构设计(Architecture Design)
Low rank approximation
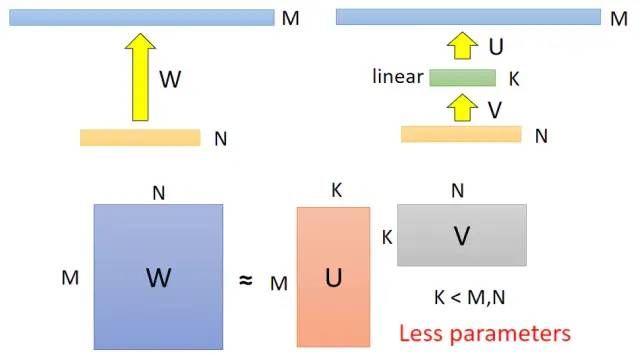
对于前馈网络来说我们可以尝试在两层之间添加一个神经元较少的层来达到减少参数的目的,比如在下图中我们在节点数为M和N的两层之间添加一个节点数为K的层,K比起M和N一般较小,则参数量由M×N变为K×(M+N):
CNN的重新设计
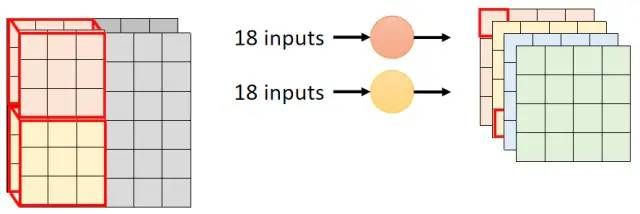
在下图中CNN的卷积过程需要处理输入的两个channel,用到了4个卷积核,最终得到4个channel的feature map,整个过程需要72个参数:
现在对这个卷积的过程做一下重新设计,使得这个过程分成两步完成:
①Depthwise Convolution
第一步卷积核的数量与输入的channel的数量相等,而且每个卷积核只负责一个channel,卷积核的大小仍然是上述3×3,这样就会获得2个channel的feature map。由于每个卷积核只负责一个channel,所以得到的feature map没有考虑输入的不同channel之间的联系:
②Pointwise Convolution
然后用4个1×1(这些卷积核大小始终为1×1)且2个channel的卷积核对上面得到的feature map进行卷积最终得到4个4×4的feature map,由此就将卷积的过程拆成了两个部分:
整个过程一共使用了3×3×2+2×4=24个参数,相比72个参数大大减少了需要的参数量。
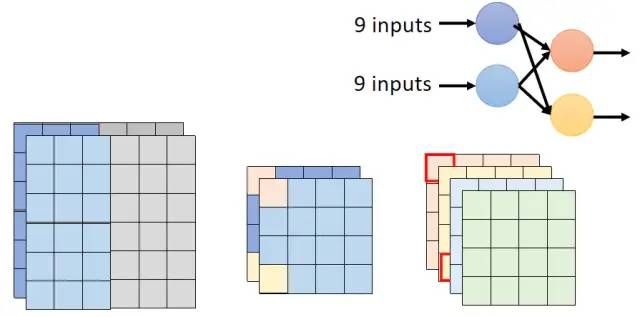
接下来对比一下原来的和重新设计的卷积过程。原来的卷积过程对于输出中不同的channel的输出用到了不同的参数(因为使用了不同的卷积核),每个卷积核都需要18个输入:
而重新设计的卷积过程中相当于Depthwise Convolution过程中的2个卷积核是公用的,每个卷积核需要9个输入,然后对于最终输出的feature map中不同channel的输出只需要用不同的1×1卷积核处理即可得到:
接下来泛化地看一下重新设计的卷积过程对减少参数量的作用。我们用代表输入的channel数,用代表输出的channel数,代表卷积核的size,则我们得到两个过程需要的参数量如下:
将两个参数量相除可以得到:
一般很大所以可以忽略不计。如果取的话,则会缩小到原来参数量的,因此这种方法对模型的压缩效果比较明显。
六、动态计算(Dynamic Computation)
我们希望模型能够根据设备的计算能力动态地调整需要的计算资源,比如在移动设备电量低时模型不应该消耗过多的计算资源。有一种实现的方式就是训练多个不同规模的模型,但是这种方式就要消耗较大的存储空间来保存模型。
这里介绍一种使用intermedia layer的方法,也就是在模型的中间层接输出层来使得模型可以在浅层直接输出结果,虽然会损失一定的准确率但是可以消耗较少的资源:
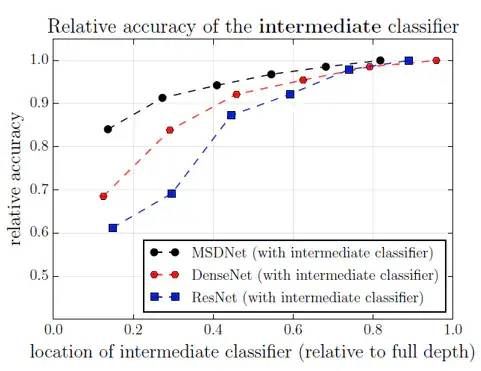
下图展示了在不同深度的中间层添加intermedia layer时intermedia layer的准确率,可以看到在浅层很难得到较高的准确率,这是因为浅层只会抽取一些简单的feature,因此不会效果很好:
下图展示了在不同深度的中间层添加intermedia layer时最终输出层的准确率,可以看到在浅层添加intermedia layer可能会造成最终输出层准确率的下降,这是因为强迫浅层输出正确的分类结果会破坏模型的架构,最终对最终的输出层造成一定影响。