Python吴恩达深度学习作业18 -- 手把手实现循环神经网络(RNN)
手把手实现循环神经网络
在此作业中,你将使用numpy实现你的第一个循环神经网络。
循环神经网络(RNN)在解决自然语言处理和其他序列任务上非常有效,因为它们具有“记忆”,可以一次读取一个输入 x < t > x^{
符号:
- 上标 [ l ] [l] [l]表示与 l t h l^{th} lth层关联的对象。
- 例如: a [ 4 ] a^{[4]} a[4]是 4 t h 4^{th} 4th层激活。 W [ 5 ] W^{[5]} W[5]和 b [ 5 ] b^{[5]} b[5]是 5 t h 5{th} 5th层参数。
- 上标 ( i ) (i) (i)表示与 i t h i^{th} ith示例关联的对象。
- 示例: x ( i ) x^{(i)} x(i)是 i t h i^{th} ith训练示例输入。
- 上标 < t > {
} <t>表示在 t t h t^{th} tth时间步的对象。- 示例: x < t > x^{
} x<t>是在 t t h t^{th} tth时间步的输入 x x x。 x ( i ) < t > x^{(i)} x(i)<t>是示例 i i i的 t t h t^{th} tth时间步的输入。
- 示例: x < t > x^{
- 下标 i i i表示向量的 i t h i^{th} ith条目。
- 示例: a i [ l ] a_i^{[l]} ai[l]表示层 l l l中激活的 i t h i^{th} ith条目。
import numpy as np
import rnn_utils
1 循环神经网络的正向传播
在本周之后的作业,你将使用RNN生成音乐。你将实现的基本RNN具有以下结构。在此示例中, T x = T y T_x=T_y Tx=Ty。
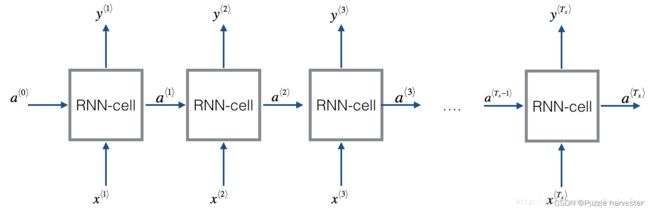
实现RNN的方法:
步骤:
- 实现RNN的一个时间步所需的计算。
- 在 T x T_x Tx个时间步上实现循环,以便一次处理所有输入。
1.1 RNN单元
循环神经网络可以看作是单个cell的重复。你首先要在单个时间步上实现计算。下图描述了RNN单元的单个时间步的操作。
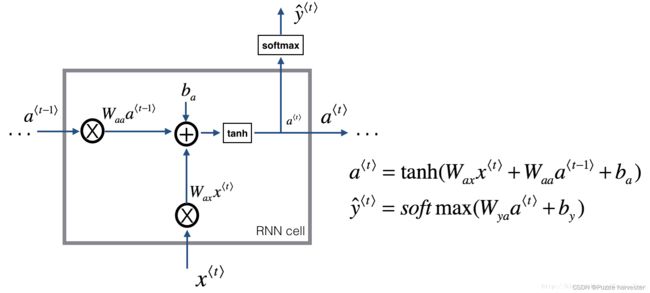
基础RNN单元,将 x < t > x^{
练习:实现上图中描述的RNN单元。
说明:
- 使用tanh激活计算隐藏状态: a ⟨ t ⟩ = tanh ( W a a a ⟨ t − 1 ⟩ + W a x x ⟨ t ⟩ + b a ) a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a) a⟨t⟩=tanh(Waaa⟨t−1⟩+Waxx⟨t⟩+ba)。
- 使用新的隐藏状态 a < t > a^{
} a<t>,计算预测 y ^ ⟨ t ⟩ = s o f t m a x ( W y a a ⟨ t ⟩ + b y ) \hat{y}^{\langle t \rangle} = softmax(W_{ya} a^{\langle t \rangle} + b_y) y^⟨t⟩=softmax(Wyaa⟨t⟩+by)。我们为你提供了一个函数:softmax。 - 将 ( a ⟨ t ⟩ , a ⟨ t − 1 ⟩ , x ⟨ t ⟩ , p a r a m e t e r s ) (a^{\langle t \rangle}, a^{\langle t-1 \rangle}, x^{\langle t \rangle}, parameters) (a⟨t⟩,a⟨t−1⟩,x⟨t⟩,parameters)存储在缓存中。
- 返回 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ , y ⟨ t ⟩ y^{\langle t \rangle} y⟨t⟩并缓存。
我们将对 m m m个示例进行向量化处理。因此, x ⟨ t ⟩ x^{\langle t \rangle} x⟨t⟩维度将是 ( n x , m ) (n_x,m) (nx,m),而 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩维度将是 ( n a , m ) (n_a,m) (na,m)。
def rnn_cell_forward(xt, a_prev, parameters):
"""
根据图2实现RNN单元的单步前向传播
参数:
xt -- 时间步"t"输入的数据,维度为(n_x, m)
a_prev -- 时间步"t - 1"的隐藏状态,维度为(n_a, m)
parameters -- 字典,包含了以下内容:
Wax -- 矩阵,输入乘以权重,维度为(n_a, n_x)
Waa -- 矩阵,隐藏状态乘以权重,维度为(n_a, n_a)
Wya -- 矩阵,隐藏状态与输出相关的权重矩阵,维度为(n_y, n_a)
ba -- 偏置,维度为(n_a, 1)
by -- 偏置,隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a_next -- 下一个隐藏状态,维度为(n_a, m)
yt_pred -- 在时间步“t”的预测,维度为(n_y, m)
cache -- 反向传播需要的元组,包含了(a_next, a_prev, xt, parameters)
"""
# 从“parameters”获取参数
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# 使用上面的公式计算下一个激活值
a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
# 使用上面的公式计算当前单元的输出
yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
# 保存反向传播需要的值
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)
a_next[4] = [ 0.59584544 0.18141802 0.61311866 0.99808218 0.85016201 0.99980978
-0.18887155 0.99815551 0.6531151 0.82872037]
a_next.shape = (5, 10)
yt_pred[1] = [0.9888161 0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
0.36920224 0.9966312 0.9982559 0.17746526]
yt_pred.shape = (2, 10)
1.2 RNN正向传播
你可以将RNN视为刚刚构建的单元的重复。如果输入的数据序列经过10个时间步长,则将复制RNN单元10次。每个单元格都将前一个单元格( a ⟨ t − 1 ⟩ a^{\langle t-1 \rangle} a⟨t−1⟩)的隐藏状态和当前时间步的输入数据( x ⟨ t ⟩ x^{\langle t \rangle} x⟨t⟩)作为输入,并为此时间步输出隐藏状态( a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩)和预测( y ⟨ t ⟩ y^{\langle t \rangle} y⟨t⟩)。
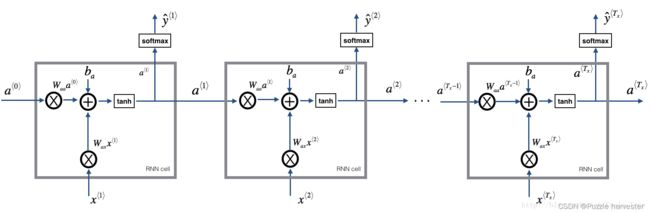
基本RNN。输入序列 x = ( x ⟨ 1 ⟩ , x ⟨ 2 ⟩ , . . . , x ⟨ T x ⟩ ) x = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle}) x=(x⟨1⟩,x⟨2⟩,...,x⟨Tx⟩)执行 T x T_x Tx个时间步。网络输出 y = ( y ⟨ 1 ⟩ , y ⟨ 2 ⟩ , . . . , y ⟨ T x ⟩ ) y = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle}) y=(y⟨1⟩,y⟨2⟩,...,y⟨Tx⟩)。
练习:编码实现上图中描述的RNN的正向传播。
说明:
- 创建一个零向量 ( a ) (a) (a),该向量将存储RNN计算的所有隐藏状态。
- 将“下一个”隐藏状态初始化为 a 0 a_0 a0(初始隐藏状态)。
- 开始遍历每个时间步,增量索引为 t t t:
- 通过运行
rnn_step_forward更新“下一个”隐藏状态和缓存。 - 将“下一个”隐藏状态存储在 a a a中( t t h t^{th} tth位置)
- 将预测存储在 y y y中
- 将缓存添加到缓存列表中
- 通过运行
- 返回 a a a, y y y和缓存。
def rnn_forward(x, a0, parameters):
"""
根据图3来实现循环神经网络的前向传播
参数:
x -- 输入的全部数据,维度为(n_x, m, T_x)
a0 -- 初始化隐藏状态,维度为 (n_a, m)
parameters -- 字典,包含了以下内容:
Wax -- 矩阵,输入乘以权重,维度为(n_a, n_x)
Waa -- 矩阵,隐藏状态乘以权重,维度为(n_a, n_a)
Wya -- 矩阵,隐藏状态与输出相关的权重矩阵,维度为(n_y, n_a)
ba -- 偏置,维度为(n_a, 1)
by -- 偏置,隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a -- 所有时间步的隐藏状态,维度为(n_a, m, T_x)
y_pred -- 所有时间步的预测,维度为(n_y, m, T_x)
caches -- 为反向传播的保存的元组,维度为(【列表类型】cache, x))
"""
# 初始化“caches”,它将以列表类型包含所有的cache
caches = []
# 获取 x 与 Wya 的维度信息
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# 使用0来初始化“a” 与“y”
a = np.zeros([n_a, m, T_x])
y_pred = np.zeros([n_y, m, T_x])
# 初始化“next”
a_next = a0
# 遍历所有时间步
for t in range(T_x):
## 1.使用rnn_cell_forward函数来更新“next”隐藏状态与cache。
a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
## 2.使用 a 来保存“next”隐藏状态(第 t )个位置。
a[:, :, t] = a_next
## 3.使用 y 来保存预测值。
y_pred[:, :, t] = yt_pred
## 4.把cache保存到“caches”列表中。
caches.append(cache)
# 保存反向传播所需要的参数
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}
a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])
print("len(caches) = ", len(caches))
a[4][1] = [-0.99999375 0.77911235 -0.99861469 -0.99833267]
a.shape = (5, 10, 4)
y_pred[1][3] = [0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape = (2, 10, 4)
caches[1][1][3] = [-1.1425182 -0.34934272 -0.20889423 0.58662319]
len(caches) = 2
Nice!你已经从头实现了循环神经网络的正向传播。对于某些应用来说,这已经足够好,但是会遇到梯度消失的问题。因此,当每个输出 y ⟨ t ⟩ y^{\langle t \rangle} y⟨t⟩主要使用"local"上下文进行估算时它表现最好(即来自输入 x ⟨ t ′ ⟩ x^{\langle t' \rangle} x⟨t′⟩的信息,其中 t ′ t' t′是距离 t t t较近)。
在下一部分中,你将构建一个更复杂的LSTM模型,该模型更适合解决逐渐消失的梯度。LSTM将能够更好地记住一条信息并将其保存许多个时间步。
2 长短期记忆网络(LSTM)
LSTM单元,这会在每个时间步上跟踪并更新“单元状态”或存储的变量 c ⟨ t ⟩ c^{\langle t \rangle} c⟨t⟩,与 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩不同。
与上面的RNN示例类似,你将以单个时间步开始实现LSTM单元。然后,你可以从for循环内部迭代调用它,以使其具有 T x T_x Tx时间步长的输入。
2.0 关于“门”
遗忘门
为了便于说明,假设我们正在阅读一段文本中的单词,并希望使用LSTM跟踪语法结构,例如主体是单数还是复数。如果主体从单数变为复数,我们需要找到一种方法来摆脱以前存储的单/复数状态的内存值。在LSTM中,遗忘门可以实现次数操作:
Γ f ⟨ t ⟩ = σ ( W f [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b f ) (1) \Gamma_f^{\langle t \rangle} = \sigma(W_f[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_f)\tag{1} Γf⟨t⟩=σ(Wf[a⟨t−1⟩,x⟨t⟩]+bf)(1)
在这里, W f W_f Wf是控制遗忘门行为的权重。我们将 [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] [a^{\langle t-1 \rangle}, x^{\langle t \rangle}] [a⟨t−1⟩,x⟨t⟩]连接起来,然后乘以 W f W_f Wf。上面的等式使得向量 Γ f ⟨ t ⟩ \Gamma_f^{\langle t \rangle} Γf⟨t⟩的值介于0到1之间。该遗忘门向量将逐元素乘以先前的单元状态 c ⟨ t − 1 ⟩ c^{\langle t-1 \rangle} c⟨t−1⟩。因此,如果 Γ f ⟨ t ⟩ \Gamma_f^{\langle t \rangle} Γf⟨t⟩的其中一个值为0(或接近于0),则表示LSTM应该移除 c ⟨ t − 1 ⟩ c^{\langle t-1 \rangle} c⟨t−1⟩组件中的一部分信息(例如,单数主题),如果其中一个值为1,则它将保留信息。
更新门
一旦我们忘记了所讨论的主体是单数,就需要找到一种更新它的方式,以反映新主体现在是复数。这是更新门的公式:
Γ u ⟨ t ⟩ = σ ( W u [ a ⟨ t − 1 ⟩ , x { t } ] + b u ) (2) \Gamma_u^{\langle t \rangle} = \sigma(W_u[a^{\langle t-1 \rangle}, x^{\{t\}}] + b_u)\tag{2} Γu⟨t⟩=σ(Wu[a⟨t−1⟩,x{t}]+bu)(2)
类似于遗忘门,在这里 Γ u ⟨ t ⟩ \Gamma_u^{\langle t \rangle} Γu⟨t⟩也是值为0到1之间的向量。这将与 c ~ ⟨ t ⟩ \tilde{c}^{\langle t \rangle} c~⟨t⟩逐元素相乘以计算 c ⟨ t ⟩ c^{\langle t \rangle} c⟨t⟩。
更新单元格
要更新新主体,我们需要创建一个新的数字向量,可以将其添加到先前的单元格状态中。我们使用的等式是:
c ~ ⟨ t ⟩ = tanh ( W c [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b c ) (3) \tilde{c}^{\langle t \rangle} = \tanh(W_c[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_c)\tag{3} c~⟨t⟩=tanh(Wc[a⟨t−1⟩,x⟨t⟩]+bc)(3)
最后,新的单元状态为:
c ⟨ t ⟩ = Γ f ⟨ t ⟩ ∗ c ⟨ t − 1 ⟩ + Γ u ⟨ t ⟩ ∗ c ~ ⟨ t ⟩ (4) c^{\langle t \rangle} = \Gamma_f^{\langle t \rangle}* c^{\langle t-1 \rangle} + \Gamma_u^{\langle t \rangle} *\tilde{c}^{\langle t \rangle} \tag{4} c⟨t⟩=Γf⟨t⟩∗c⟨t−1⟩+Γu⟨t⟩∗c~⟨t⟩(4)
输出门
为了确定我们将使用哪些输出,我们将使用以下两个公式:
Γ o ⟨ t ⟩ = σ ( W o [ a ⟨ t − 1 ⟩ , x ⟨ t ⟩ ] + b o ) (5) \Gamma_o^{\langle t \rangle}= \sigma(W_o[a^{\langle t-1 \rangle}, x^{\langle t \rangle}] + b_o)\tag{5} Γo⟨t⟩=σ(Wo[a⟨t−1⟩,x⟨t⟩]+bo)(5)
a ⟨ t ⟩ = Γ o ⟨ t ⟩ ∗ tanh ( c ⟨ t ⟩ ) (6) a^{\langle t \rangle} = \Gamma_o^{\langle t \rangle}* \tanh(c^{\langle t \rangle})\tag{6} a⟨t⟩=Γo⟨t⟩∗tanh(c⟨t⟩)(6)
在等式5中,你决定使用sigmoid函数输出;在等式6中,将其乘以先前状态的tanh。
2.1 LSTM单元
练习:实现上图中描述的LSTM单元。
说明:
- 将 a ⟨ t − 1 ⟩ a^{\langle t-1 \rangle} a⟨t−1⟩和 x ⟨ t ⟩ x^{\langle t \rangle} x⟨t⟩连接在一个矩阵中: c o n c a t = [ a ⟨ t − 1 ⟩ x ⟨ t ⟩ ] concat = \begin{bmatrix} a^{\langle t-1 \rangle} \\ x^{\langle t \rangle} \end{bmatrix} concat=[a⟨t−1⟩x⟨t⟩]
- 计算公式1 - 6,你可以使用
sigmoid()和np.tanh()。 - 计算预测 y ⟨ t ⟩ y^{\langle t \rangle} y⟨t⟩,你可以使用
sigmoid()。
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
根据图4实现一个LSTM单元的前向传播。
参数:
xt -- 在时间步“t”输入的数据,维度为(n_x, m)
a_prev -- 上一个时间步“t-1”的隐藏状态,维度为(n_a, m)
c_prev -- 上一个时间步“t-1”的记忆状态,维度为(n_a, m)
parameters -- 字典类型的变量,包含了:
Wf -- 遗忘门的权值,维度为(n_a, n_a + n_x)
bf -- 遗忘门的偏置,维度为(n_a, 1)
Wi -- 更新门的权值,维度为(n_a, n_a + n_x)
bi -- 更新门的偏置,维度为(n_a, 1)
Wc -- 第一个“tanh”的权值,维度为(n_a, n_a + n_x)
bc -- 第一个“tanh”的偏置,维度为(n_a, n_a + n_x)
Wo -- 输出门的权值,维度为(n_a, n_a + n_x)
bo -- 输出门的偏置,维度为(n_a, 1)
Wy -- 隐藏状态与输出相关的权值,维度为(n_y, n_a)
by -- 隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a_next -- 下一个隐藏状态,维度为(n_a, m)
c_next -- 下一个记忆状态,维度为(n_a, m)
yt_pred -- 在时间步“t”的预测,维度为(n_y, m)
cache -- 包含了反向传播所需要的参数,包含了(a_next, c_next, a_prev, c_prev, xt, parameters)
注意:
ft/it/ot表示遗忘/更新/输出门,cct表示候选值(c tilda),c表示记忆值。
"""
# 从“parameters”中获取相关值
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 获取 xt 与 Wy 的维度信息
n_x, m = xt.shape
n_y, n_a = Wy.shape
# 1.连接 a_prev 与 xt
contact = np.zeros([n_a + n_x, m])
contact[: n_a, :] = a_prev
contact[n_a :, :] = xt
# 2.根据公式计算ft、it、cct、c_next、ot、a_next
## 遗忘门,公式1
ft = rnn_utils.sigmoid(np.dot(Wf, contact) + bf)
## 更新门,公式2
it = rnn_utils.sigmoid(np.dot(Wi, contact) + bi)
## 更新单元,公式3
cct = np.tanh(np.dot(Wc, contact) + bc)
## 更新单元,公式4
#c_next = np.multiply(ft, c_prev) + np.multiply(it, cct)
c_next = ft * c_prev + it * cct
## 输出门,公式5
ot = rnn_utils.sigmoid(np.dot(Wo, contact) + bo)
## 输出门,公式6
#a_next = np.multiply(ot, np.tan(c_next))
a_next = ot * np.tanh(c_next)
# 3.计算LSTM单元的预测值
yt_pred = rnn_utils.softmax(np.dot(Wy, a_next) + by)
# 保存包含了反向传播所需要的参数
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][3])
print("len(cache) = ", len(cache))
a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
cache[1][3] = [-0.16263996 1.03729328 0.72938082 -0.54101719 0.02752074 -0.30821874
0.07651101 -1.03752894 1.41219977 -0.37647422]
len(cache) = 10
2.2 LSTM的正向传播
既然你已经实现了LSTM的一个步骤,现在就可以使用for循环在 T x T_x Tx输入序列上对此进行迭代。
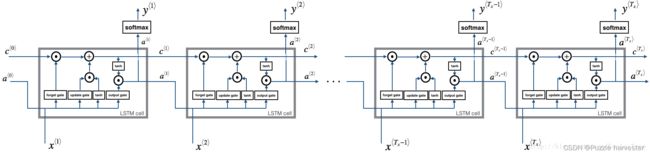
练习:实现lstm_forward()以在 T x T_x Tx个时间步上运行LSTM。
注意: c ⟨ 0 ⟩ c^{\langle 0 \rangle} c⟨0⟩用零初始化。
def lstm_forward(x, a0, parameters):
"""
根据图5来实现LSTM单元组成的的循环神经网络
参数:
x -- 所有时间步的输入数据,维度为(n_x, m, T_x)
a0 -- 初始化隐藏状态,维度为(n_a, m)
parameters -- python字典,包含了以下参数:
Wf -- 遗忘门的权值,维度为(n_a, n_a + n_x)
bf -- 遗忘门的偏置,维度为(n_a, 1)
Wi -- 更新门的权值,维度为(n_a, n_a + n_x)
bi -- 更新门的偏置,维度为(n_a, 1)
Wc -- 第一个“tanh”的权值,维度为(n_a, n_a + n_x)
bc -- 第一个“tanh”的偏置,维度为(n_a, n_a + n_x)
Wo -- 输出门的权值,维度为(n_a, n_a + n_x)
bo -- 输出门的偏置,维度为(n_a, 1)
Wy -- 隐藏状态与输出相关的权值,维度为(n_y, n_a)
by -- 隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a -- 所有时间步的隐藏状态,维度为(n_a, m, T_x)
y -- 所有时间步的预测值,维度为(n_y, m, T_x)
caches -- 为反向传播的保存的元组,维度为(【列表类型】cache, x))
"""
# 初始化“caches”
caches = []
# 获取 xt 与 Wy 的维度信息
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# 使用0来初始化“a”、“c”、“y”
a = np.zeros([n_a, m, T_x])
c = np.zeros([n_a, m, T_x])
y = np.zeros([n_y, m, T_x])
# 初始化“a_next”、“c_next”
a_next = a0
c_next = np.zeros([n_a, m])
# 遍历所有的时间步
for t in range(T_x):
# 更新下一个隐藏状态,下一个记忆状态,计算预测值,获取cache
a_next, c_next, yt_pred, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
# 保存新的下一个隐藏状态到变量a中
a[:, :, t] = a_next
# 保存预测值到变量y中
y[:, :, t] = yt_pred
# 保存下一个单元状态到变量c中
c[:, :, t] = c_next
# 把cache添加到caches中
caches.append(cache)
# 保存反向传播需要的参数
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])
print("c[1][2][1]", c[1][2][1])
print("len(caches) = ", len(caches))
a[4][3][6] = 0.17211776753291672
a.shape = (5, 10, 7)
y[1][4][3] = 0.9508734618501101
y.shape = (2, 10, 7)
caches[1][1[1]] = [ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.8555449167181981
len(caches) = 2
3 循环神经网络中的反向传播
在现代深度学习框架中,你仅需实现正向传播,而框架将处理反向传播,因此大多数深度学习工程师无需理会反向传播的细节。但是,如果你是微积分专家并且想查看RNN中反向传播的详细信息,则可以学习此笔记本的剩余部分。
在较早的课程中,当你实现了一个简单的(全连接的)神经网络时,你就使用了反向传播来计算用于更新参数的损失的导数。同样,在循环神经网络中,你可以计算损失的导数以更新参数。反向传播方程非常复杂,我们在讲座中没有导出它们。但是,我们将在下面简要介绍它们。
3.1 基础RNN的反向传播
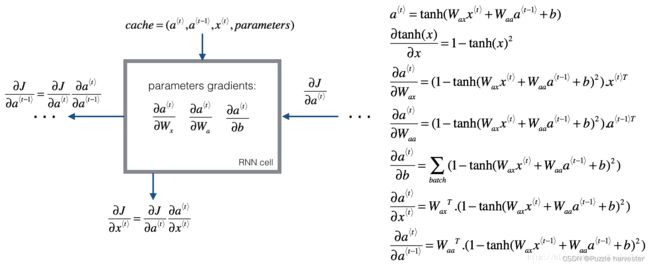
就像在全连接的神经网络中一样,损失函数 J J J的导数遵循链规则在RNN中计算反向传播。链规则还用于计算 ( ∂ J ∂ W a x , ∂ J ∂ W a a , ∂ J ∂ b ) (\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b}) (∂Wax∂J,∂Waa∂J,∂b∂J)更新参数 ( W a x , W a a , b a ) (W_{ax}, W_{aa}, b_a) (Wax,Waa,ba)。
3.1.1 反向求导函数:
要计算rnn_cell_backward,你需要计算以下方程式。手工导出它们是一个很好的练习。
tanh \tanh tanh的导数为 1 − tanh ( x ) 2 1-\tanh(x)^2 1−tanh(x)2。你可以在here中找到完整的证明。请注意:$ \text{sech}(x)^2 = 1 - \tanh(x)^2$
同样,对于 ∂ a ⟨ t ⟩ ∂ W a x , ∂ a ⟨ t ⟩ ∂ W a a , ∂ a ⟨ t ⟩ ∂ b \frac{ \partial a^{\langle t \rangle} } {\partial W_{ax}}, \frac{ \partial a^{\langle t \rangle} } {\partial W_{aa}}, \frac{ \partial a^{\langle t \rangle} } {\partial b} ∂Wax∂a⟨t⟩,∂Waa∂a⟨t⟩,∂b∂a⟨t⟩, tanh ( u ) \tanh(u) tanh(u)导数为 ( 1 − tanh ( u ) 2 ) d u (1-\tanh(u)^2)du (1−tanh(u)2)du。
最后两个方程式也遵循相同的规则,并使用 tanh \tanh tanh导数导出。请注意,这种安排是为了获得相同的维度以方便匹配的。
def rnn_cell_backward(da_next, cache):
"""
实现基本的RNN单元的单步反向传播
参数:
da_next -- 关于下一个隐藏状态的损失的梯度。
cache -- 字典类型,rnn_step_forward()的输出
返回:
gradients -- 字典,包含了以下参数:
dx -- 输入数据的梯度,维度为(n_x, m)
da_prev -- 上一隐藏层的隐藏状态,维度为(n_a, m)
dWax -- 输入到隐藏状态的权重的梯度,维度为(n_a, n_x)
dWaa -- 隐藏状态到隐藏状态的权重的梯度,维度为(n_a, n_a)
dba -- 偏置向量的梯度,维度为(n_a, 1)
"""
# 获取cache 的值
a_next, a_prev, xt, parameters = cache
# 从 parameters 中获取参数
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# 计算tanh相对于a_next的梯度.
dtanh = (1 - np.square(a_next)) * da_next
# 计算关于Wax损失的梯度
dxt = np.dot(Wax.T,dtanh)
dWax = np.dot(dtanh, xt.T)
# 计算关于Waa损失的梯度
da_prev = np.dot(Waa.T,dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# 计算关于b损失的梯度
dba = np.sum(dtanh, keepdims=True, axis=-1)
# 保存这些梯度到字典内
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
b = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)
da_next = np.random.randn(5,10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
gradients["dxt"][1][2] = -0.4605641030588796
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = 0.08429686538067718
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.3930818739219304
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = -0.2848395578696067
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.80517166]
gradients["dba"].shape = (5, 1)
3.1.2 反向传播
在每个时间步长 t t t上计算相对于 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩的损失梯度非常有用,因为它有助于将梯度反向传播到先前的RNN单元。为此,你需要从头开始遍历所有时间步,并且在每一步中,增加总的 d b a db_a dba, d W a a dW_{aa} dWaa, d W a x dW_{ax} dWax并存储 d x dx dx。
说明:
实现rnn_backward函数。首先用零初始化返回变量,然后循环遍历所有时间步,同时在每个时间步调用rnn_cell_backward,相应地更新其他变量。
def rnn_backward(da, caches):
"""
在整个输入数据序列上实现RNN的反向传播
参数:
da -- 所有隐藏状态的梯度,维度为(n_a, m, T_x)
caches -- 包含向前传播的信息的元组
返回:
gradients -- 包含了梯度的字典:
dx -- 关于输入数据的梯度,维度为(n_x, m, T_x)
da0 -- 关于初始化隐藏状态的梯度,维度为(n_a, m)
dWax -- 关于输入权重的梯度,维度为(n_a, n_x)
dWaa -- 关于隐藏状态的权值的梯度,维度为(n_a, n_a)
dba -- 关于偏置的梯度,维度为(n_a, 1)
"""
# 从caches中获取第一个cache(t=1)的值
caches, x = caches
a1, a0, x1, parameters = caches[0]
# 获取da与x1的维度信息
n_a, m, T_x = da.shape
n_x, m = x1.shape
# 初始化梯度
dx = np.zeros([n_x, m, T_x])
dWax = np.zeros([n_a, n_x])
dWaa = np.zeros([n_a, n_a])
dba = np.zeros([n_a, 1])
da0 = np.zeros([n_a, m])
da_prevt = np.zeros([n_a, m])
# 处理所有时间步
for t in reversed(range(T_x)):
# 计算时间步“t”时的梯度
gradients = rnn_cell_backward(da[:, :, t] + da_prevt, caches[t])
#从梯度中获取导数
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# 通过在时间步t添加它们的导数来增加关于全局导数的参数
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
#将 da0设置为a的梯度,该梯度已通过所有时间步骤进行反向传播
da0 = da_prevt
#保存这些梯度到字典内
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
gradients["dx"][1][2] = [-2.07101689 -0.59255627 0.02466855 0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.31494237512664996
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.264104496527777
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.3033331265798935
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)
3.2 LSTM反向传播
3.2.1 反向传播一步
LSTM反向传播比正向传播要复杂得多。我们在下面为你提供了LSTM反向传播的所有方程式。(如果你喜欢微积分练习,可以尝试从头开始自己演算)
3.2.2 门求导
d Γ o ⟨ t ⟩ = d a n e x t ∗ tanh ( c n e x t ) ∗ Γ o ⟨ t ⟩ ∗ ( 1 − Γ o ⟨ t ⟩ ) (7) d \Gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*(1-\Gamma_o^{\langle t \rangle})\tag{7} dΓo⟨t⟩=danext∗tanh(cnext)∗Γo⟨t⟩∗(1−Γo⟨t⟩)(7)
d c ~ ⟨ t ⟩ = ( d c n e x t ∗ Γ u ⟨ t ⟩ + Γ o ⟨ t ⟩ ( 1 − tanh ( c n e x t ) 2 ) ∗ i t ∗ d a n e x t ∗ c ~ ⟨ t ⟩ ) ∗ ( 1 − tanh ( c ~ ) 2 ) (8) d\tilde c^{\langle t \rangle} = (dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * i_t * da_{next} * \tilde c^{\langle t \rangle}) * (1-\tanh(\tilde c)^2) \tag{8} dc~⟨t⟩=(dcnext∗Γu⟨t⟩+Γo⟨t⟩(1−tanh(cnext)2)∗it∗danext∗c~⟨t⟩)∗(1−tanh(c~)2)(8)
d Γ u ⟨ t ⟩ = ( d c n e x t ∗ c ~ ⟨ t ⟩ + Γ o ⟨ t ⟩ ( 1 − tanh ( c n e x t ) 2 ) ∗ c ~ ⟨ t ⟩ ∗ d a n e x t ) ∗ Γ u ⟨ t ⟩ ∗ ( 1 − Γ u ⟨ t ⟩ ) (9) d\Gamma_u^{\langle t \rangle} = (dc_{next}*\tilde c^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * \tilde c^{\langle t \rangle} * da_{next})*\Gamma_u^{\langle t \rangle}*(1-\Gamma_u^{\langle t \rangle})\tag{9} dΓu⟨t⟩=(dcnext∗c~⟨t⟩+Γo⟨t⟩(1−tanh(cnext)2)∗c~⟨t⟩∗danext)∗Γu⟨t⟩∗(1−Γu⟨t⟩)(9)
d Γ f ⟨ t ⟩ = ( d c n e x t ∗ c ~ p r e v + Γ o ⟨ t ⟩ ( 1 − tanh ( c n e x t ) 2 ) ∗ c p r e v ∗ d a n e x t ) ∗ Γ f ⟨ t ⟩ ∗ ( 1 − Γ f ⟨ t ⟩ ) (10) d\Gamma_f^{\langle t \rangle} = (dc_{next}*\tilde c_{prev} + \Gamma_o^{\langle t \rangle} (1-\tanh(c_{next})^2) * c_{prev} * da_{next})*\Gamma_f^{\langle t \rangle}*(1-\Gamma_f^{\langle t \rangle})\tag{10} dΓf⟨t⟩=(dcnext∗c~prev+Γo⟨t⟩(1−tanh(cnext)2)∗cprev∗danext)∗Γf⟨t⟩∗(1−Γf⟨t⟩)(10)
3.2.3 参数求导
d W f = d Γ f ⟨ t ⟩ ∗ ( a p r e v x t ) T (11) dW_f = d\Gamma_f^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{11} dWf=dΓf⟨t⟩∗(aprevxt)T(11)
d W u = d Γ u ⟨ t ⟩ ∗ ( a p r e v x t ) T (12) dW_u = d\Gamma_u^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{12} dWu=dΓu⟨t⟩∗(aprevxt)T(12)
d W c = d c ~ ⟨ t ⟩ ∗ ( a p r e v x t ) T (13) dW_c = d\tilde c^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{13} dWc=dc~⟨t⟩∗(aprevxt)T(13)
d W o = d Γ o ⟨ t ⟩ ∗ ( a p r e v x t ) T (14) dW_o = d\Gamma_o^{\langle t \rangle} * \begin{pmatrix} a_{prev} \\ x_t\end{pmatrix}^T \tag{14} dWo=dΓo⟨t⟩∗(aprevxt)T(14)
要计算 d b f , d b u , d b c , d b o db_f, db_u, db_c, db_o dbf,dbu,dbc,dbo,你只需要在 d Γ f ⟨ t ⟩ , d Γ u ⟨ t ⟩ , d c ~ ⟨ t ⟩ , d Γ o ⟨ t ⟩ d\Gamma_f^{\langle t \rangle}, d\Gamma_u^{\langle t \rangle}, d\tilde c^{\langle t \rangle}, d\Gamma_o^{\langle t \rangle} dΓf⟨t⟩,dΓu⟨t⟩,dc~⟨t⟩,dΓo⟨t⟩的水平(axis=1)轴上分别求和。注意,你应该有keep_dims = True选项。
最后,你将针对先前的隐藏状态,先前的记忆状态和输入计算导数。
d a p r e v = W f T ∗ d Γ f ⟨ t ⟩ + W u T ∗ d Γ u ⟨ t ⟩ + W c T ∗ d c ~ ⟨ t ⟩ + W o T ∗ d Γ o ⟨ t ⟩ (15) da_{prev} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c^{\langle t \rangle} + W_o^T * d\Gamma_o^{\langle t \rangle} \tag{15} daprev=WfT∗dΓf⟨t⟩+WuT∗dΓu⟨t⟩+WcT∗dc~⟨t⟩+WoT∗dΓo⟨t⟩(15)
在这里,等式13的权重是第n_a个(即 W f = W f [ : , : n a ] W_f = W_f[:,:n_a] Wf=Wf[:,:na]等…)
d c p r e v = d c n e x t Γ f ⟨ t ⟩ + Γ o ⟨ t ⟩ ∗ ( 1 − tanh ( c n e x t ) 2 ) ∗ Γ f ⟨ t ⟩ ∗ d a n e x t (16) dc_{prev} = dc_{next}\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh(c_{next})^2)*\Gamma_f^{\langle t \rangle}*da_{next} \tag{16} dcprev=dcnextΓf⟨t⟩+Γo⟨t⟩∗(1−tanh(cnext)2)∗Γf⟨t⟩∗danext(16)
d x ⟨ t ⟩ = W f T ∗ d Γ f ⟨ t ⟩ + W u T ∗ d Γ u ⟨ t ⟩ + W c T ∗ d c ~ t + W o T ∗ d Γ o ⟨ t ⟩ (17) dx^{\langle t \rangle} = W_f^T*d\Gamma_f^{\langle t \rangle} + W_u^T * d\Gamma_u^{\langle t \rangle}+ W_c^T * d\tilde c_t + W_o^T * d\Gamma_o^{\langle t \rangle}\tag{17} dx⟨t⟩=WfT∗dΓf⟨t⟩+WuT∗dΓu⟨t⟩+WcT∗dc~t+WoT∗dΓo⟨t⟩(17)
其中等式15的权重是从n_a到末尾(即 W f = W f [ : , n a : ] W_f = W_f[:,n_a:] Wf=Wf[:,na:]等…)
练习:通过实现下面的等式来实现lstm_cell_backward。
def lstm_cell_backward(da_next, dc_next, cache):
"""
实现LSTM的单步反向传播
参数:
da_next -- 下一个隐藏状态的梯度,维度为(n_a, m)
dc_next -- 下一个单元状态的梯度,维度为(n_a, m)
cache -- 来自前向传播的一些参数
返回:
gradients -- 包含了梯度信息的字典:
dxt -- 输入数据的梯度,维度为(n_x, m)
da_prev -- 先前的隐藏状态的梯度,维度为(n_a, m)
dc_prev -- 前的记忆状态的梯度,维度为(n_a, m, T_x)
dWf -- 遗忘门的权值的梯度,维度为(n_a, n_a + n_x)
dbf -- 遗忘门的偏置的梯度,维度为(n_a, 1)
dWi -- 更新门的权值的梯度,维度为(n_a, n_a + n_x)
dbi -- 更新门的偏置的梯度,维度为(n_a, 1)
dWc -- 第一个“tanh”的权值的梯度,维度为(n_a, n_a + n_x)
dbc -- 第一个“tanh”的偏置的梯度,维度为(n_a, n_a + n_x)
dWo -- 输出门的权值的梯度,维度为(n_a, n_a + n_x)
dbo -- 输出门的偏置的梯度,维度为(n_a, 1)
"""
# 从cache中获取信息
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
# 获取xt与a_next的维度信息
n_x, m = xt.shape
n_a, m = a_next.shape
# 根据公式7-10来计算门的导数
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
# 根据公式11-14计算参数的导数
concat = np.concatenate((a_prev, xt), axis=0).T
dWf = np.dot(dft, concat)
dWi = np.dot(dit, concat)
dWc = np.dot(dcct, concat)
dWo = np.dot(dot, concat)
dbf = np.sum(dft,axis=1,keepdims=True)
dbi = np.sum(dit,axis=1,keepdims=True)
dbc = np.sum(dcct,axis=1,keepdims=True)
dbo = np.sum(dot,axis=1,keepdims=True)
# 使用公式15-17计算洗起来了隐藏状态、先前记忆状态、输入的导数。
da_prev = np.dot(parameters["Wf"][:, :n_a].T, dft) + np.dot(parameters["Wc"][:, :n_a].T, dcct) + np.dot(parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters["Wo"][:, :n_a].T, dot)
dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
dxt = np.dot(parameters["Wf"][:, n_a:].T, dft) + np.dot(parameters["Wc"][:, n_a:].T, dcct) + np.dot(parameters["Wi"][:, n_a:].T, dit) + np.dot(parameters["Wo"][:, n_a:].T, dot)
# 保存梯度信息到字典
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
da_next = np.random.randn(5,10)
dc_next = np.random.randn(5,10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)
gradients["dxt"][1][2] = 3.230559115109188
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.06396214197109236
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.7975220387970015
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.1479548381644968
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.0574980552259903
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.3045621636876668
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.3313115952892109
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.13893342]
gradients["dbo"].shape = (5, 1)
3.3 反向传播LSTM RNN
这部分与你在上面实现的rnn_backward函数非常相似。首先将创建与返回变量相同维度的变量。然后,你将从头开始遍历所有时间步,并在每次迭代中调用为LSTM实现的一步函数。然后,你将通过分别汇总参数来更新参数。最后返回带有新梯度的字典。
说明:实现lstm_backward函数。创建一个从 T x T_x Tx开始并向后的for循环。对于每个步骤,请调用lstm_cell_backward并通过向其添加新梯度来更新旧梯度。请注意,dxt不会更新而是存储。
def lstm_backward(da, caches):
"""
实现LSTM网络的反向传播
参数:
da -- 关于隐藏状态的梯度,维度为(n_a, m, T_x)
cachses -- 前向传播保存的信息
返回:
gradients -- 包含了梯度信息的字典:
dx -- 输入数据的梯度,维度为(n_x, m,T_x)
da0 -- 先前的隐藏状态的梯度,维度为(n_a, m)
dWf -- 遗忘门的权值的梯度,维度为(n_a, n_a + n_x)
dbf -- 遗忘门的偏置的梯度,维度为(n_a, 1)
dWi -- 更新门的权值的梯度,维度为(n_a, n_a + n_x)
dbi -- 更新门的偏置的梯度,维度为(n_a, 1)
dWc -- 第一个“tanh”的权值的梯度,维度为(n_a, n_a + n_x)
dbc -- 第一个“tanh”的偏置的梯度,维度为(n_a, n_a + n_x)
dWo -- 输出门的权值的梯度,维度为(n_a, n_a + n_x)
dbo -- 输出门的偏置的梯度,维度为(n_a, 1)
"""
# 从caches中获取第一个cache(t=1)的值
caches, x = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
# 获取da与x1的维度信息
n_a, m, T_x = da.shape
n_x, m = x1.shape
# 初始化梯度
dx = np.zeros([n_x, m, T_x])
da0 = np.zeros([n_a, m])
da_prevt = np.zeros([n_a, m])
dc_prevt = np.zeros([n_a, m])
dWf = np.zeros([n_a, n_a + n_x])
dWi = np.zeros([n_a, n_a + n_x])
dWc = np.zeros([n_a, n_a + n_x])
dWo = np.zeros([n_a, n_a + n_x])
dbf = np.zeros([n_a, 1])
dbi = np.zeros([n_a, 1])
dbc = np.zeros([n_a, 1])
dbo = np.zeros([n_a, 1])
# 处理所有时间步
for t in reversed(range(T_x)):
# 使用lstm_cell_backward函数计算所有梯度
gradients = lstm_cell_backward(da[:,:,t],dc_prevt,caches[t])
# 保存相关参数
dx[:,:,t] = gradients['dxt']
dWf = dWf+gradients['dWf']
dWi = dWi+gradients['dWi']
dWc = dWc+gradients['dWc']
dWo = dWo+gradients['dWo']
dbf = dbf+gradients['dbf']
dbi = dbi+gradients['dbi']
dbc = dbc+gradients['dbc']
dbo = dbo+gradients['dbo']
# 将第一个激活的梯度设置为反向传播的梯度da_prev。
da0 = gradients['da_prev']
# 保存所有梯度到字典变量内
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,7)
a0 = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
a, y, c, caches = lstm_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)
gradients["dx"][1][2] = [-0.00173313 0.08287442 -0.30545663 -0.43281115]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.09591150195400468
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = -0.06981985612744009
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 0.10237182024854771
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = -0.062498379492745226
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.04843891314443012
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [-0.0565788]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.15399065]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [-0.29691142]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [-0.29798344]
gradients["dbo"].shape = (5, 1)