Python统计学03——随机变量的概率分布

参考书目：贾俊平. 统计学——Python实现. 北京: 高等教育出版社，2021.

---

概率论里面的随机变量有很多分布，常见的离散型有二项分布，泊松分布，连续性的分布有正态分布，均匀分布，指数分等。分布是可以计算概率的，还有期望和方差。

首先看一个简单的加权的求期望和方差。

导入包，读取案例数据

import numpy as np
import pandas as pd

df=pd.read_csv('D:/AAA最近要用/贾老师/统计学—Python实现/（01）例题数据/pydata/chap04/example4_1.csv',encoding='gbk')
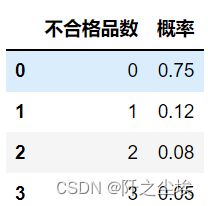
df.head()

计算均值方差

mymean=sum(df['不合格品数']*df['概率'])
myvar=sum((df['不合格品数']-mymean)**2*df['概率'])
mystd=np.sqrt(myvar)
mymean,myvar,mystd

 

---

 二项分布

原理就不过多介绍了，学过概率论一个都会，这里主要介绍怎么用Python计算概率。

第一个参数表是时间成功的个数，第二个参数表是实验了多少次，第三个是成功的概率。

#二项分布
from scipy.stats import binom
p0=binom.pmf(0,5,0.06)
p1=binom.pmf(1,5,0.06)
p2=binom.pmf(2,5,0.06)
p3=binom.pmf(3,5,0.06)
p21=binom.cdf(3,5,0.06)    #3个及其以下
print(p0+p1+p2+p3)
p0,p1,p2,p3,p21

 

---

 正态分布

#正态分布
from scipy.stats import norm
p1=norm.cdf(40,loc=50,scale=10)                                       #p(x<40概率)
p2=norm.cdf(40,loc=50,scale=10)-norm.cdf(30,loc=50,scale=10)         #p(30

离散型概率分布的函数是pmf，连续性分布的概率密度是pdf，累计分布函数都是cdf。

还有ppf，表是反函，给概率返回值。 

 

---

卡方分布

#卡方分布
from scipy.stats import chi2
p1=chi2.cdf(10,df=15)         #自由度为15时，卡方小于10的概率
p2=1-chi2.cdf(15,df=25)         #自由度为25时，卡方大于15的概率
q=chi2.ppf(0.95,df=10)          #自由度为10 ，累计概率为0.95的反函值
print(p1,p2,q)

 

---

 t分布

#t分布
from scipy.stats import t
p1=t.cdf(-2,df=10)         #自由度为10时，卡方小于-2的概率
p2=1-t.cdf(3,df=15)         #自由度为25时，t大于3的概率
q=t.ppf(0.975,df=25)          #自由度为25 ，累计概率为0.975的反函值
print(p1,p2,q)

 

---

F分布

#F分布
from scipy.stats import f
p1=f.cdf(3,10,8)         #自由度为10,8时，f小于3的概率
p2=1-f.cdf(2.5,18,15)         #自由度为18,15时，f大于2.5的概率
q=f.ppf(0.95,dfn=25,dfd=20)          #自由度为25,20 ，累计概率为0.95的反函值
print(p1,p2,q)