当我们对数据建模时,首先应该建立一个标准基线方案,然后再通过优化对该方案进行修改。在项目的第一部分中,我们必须要投入时间来理解业务需求并进行充分的探索性分析。建立一个原始模型。可以有助于理解数据,采用适当的验证策略,或为引入奇特的想法提供数据的支持。
在这个初步阶段之后,我们可以根据不同的情况选择不同的优化方式,例如改变模型,进行数据的处理,甚至是引入更多的外部数据。
对于每个方案,我们都需要对数据进行处理,建模和验证,这都需要从头开始对模型进行再训练,这时就会浪费很多的时间,如果我们可以通过一些简单而有效的技巧来提高预测的速度。例如,我们都知道特征选择是一种降低预测模型输入的特征维数的技术。特征选择是大多数机器学习管道中的一个重要步骤,主要用于提高性能。当减少特征时,就是降低了模型的复杂性,从而降低了训练和验证的时间。
在这篇文章中,我们展示了特征选择在减少预测推理时间方面的有效性,同时避免了性能的显着下降。tspiral 是一个 Python 包,它提供了各种预测技术。并且它与 scikit-learn 可以完美的集成使用。
为了进行实验,我们模拟了多个时间序列,每个小时的频率和双季节性(每日和每周)。此外我们还加入了一个从一个平滑的随机游走中得到的趋势,这样就引入了一个随机的行为。
这个时序数据的最后一部分是用作测试使用的,我们会记录其中测量预测误差和做出预测所需的时间。对于这个实验模拟了100个独立的时间序列。之所以说“独立”,是因为尽管它们表现出非常相似的行为,但所有的系列并不相互关联。通过这种方式,我们分别对它们进行建模。
我们使用目标的滞后值作为输入来预测时间序列。换句话说,为了预测下一个小时的值,我们使用表格格式重新排列了以前可用的每小时观测值。这样时间序列预测的特征选择就与标准的表格监督任务一样。这样特征选择的算法就可以简单地对滞后的目标特征进行操作。下面是一个使用递归预测进行特征选择的例子。
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import SelectFromModel
from tsprial.forecasting import ForecastingCascade
max_lags = 72
recursive_model = ForecastingCascade(
make_pipeline(
SelectFromModel(
Ridge(), threshold='median',
max_features=max_lags,
),
Ridge()
),
lags=range(1,169),
use_exog=False
)
recursive_model.fit(None, y)
selected_lags = recursive_model.estimator_['selectfrommodel'].get_support(indices=True)我们使用元估计器的重要性权重(线性模型的系数)从训练数据中选择重要特征。这是一种简单而快速的选择特征的方法,因为我们处理后的数据可以使用通常应用于表格回归任务的相同技术来执行。
在直接预测的情况下,需要为每个预测步骤拟合一个单独的估计器。需要为每个预测步骤进行选择。每个估计器会选择不同的重要程度的滞后子集,并汇总结果生成一组独特的有意义的滞后。
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import SelectFromModel
from tsprial.forecasting import ForecastingChain
max_lags = 72
direct_model = ForecastingChain(
make_pipeline(
SelectFromModel(
Ridge(), threshold='median',
),
Ridge()
),
n_estimators=168,
lags=range(1,169),
use_exog=False,
n_jobs=-1
)
direct_model.fit(None, y)
selected_lags = np.argsort(np.asarray([
est.estimator_['selectfrommodel'].get_support()
for est in direct_model.estimators_
]).sum(0))[-max_lags:]结果可以看到,滞后选择与模型性能密切相关。在纯自回归的情况下,如果没有额外的外生变量,滞后目标值是提供良好预测的唯一有价值的信息。
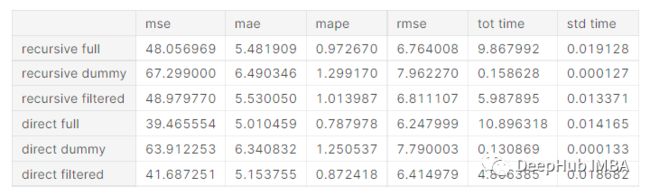
这里采用了三种递归和直接方法。首先,使用过去长达168小时的所有延迟(full)。然后,只使用周期性滞后(dummy)。最后只考虑在训练数据上选择的有意义的滞后(filtered)来拟合我们的模型
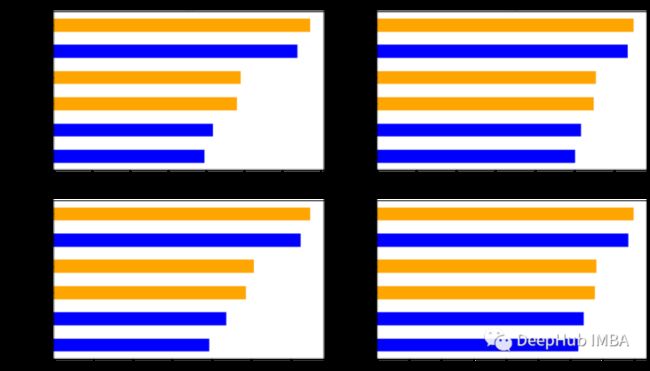
可以看到最直接方法是最准确的。而full的方法比dummy的和filter的方法性能更好,在递归的方法中,full和filtered的结果几乎相同。
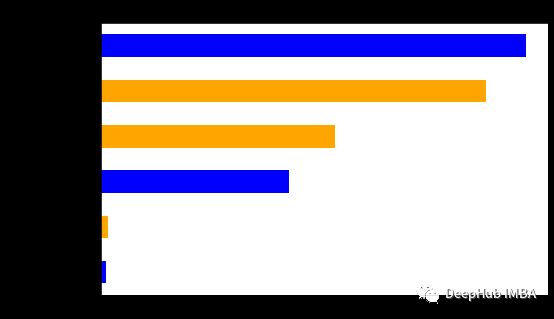
对于时间来说,dummy方法是最快的方法,这个应该是预料之中的因为它考虑的特征数量很少。出于同样的原因,filtered要比full快。但是令人惊讶的是,filtered的速度是full方法的一半。这可能是一个很好的结果,因为我们可以通过简单的特征选择以更快的方式获得良好的预测。
上面的测试结果和表格都是利用 tspiral 的来进行处理和生成的。它简化了有意义的自回归滞后的识别,并赋予了使用时间序列操作特征选择的可能性。最后我们还通过这个实验发现了如何通过简单地应用适当的滞后选择来减少预测的推理时间。
如果你对本文的结果感兴趣,请查看本文的源代码:
https://avoid.overfit.cn/post/7488218628c84fdb9423484a98bbfa3e
作者:Marco Cerliani