Verliog HDL硬件描述语言学习笔记(六)
在数字逻辑系统的设计中,对于每个部件模块的设计工作主要包括3各部分:
1.电路模块的设计
2.测试模块的设计
3.设计文档的编写和整理
其中测试模块的设计和文档的编写是设计中的2个重要的环节。测试模块编写的是否严密和完整决定了系统设计的成败;文档的编写可以很好的阐述模块的性能和为以后的调试提供方便。
而在数字逻辑系统的设计中,组合逻辑部件(如多路器、比较器、加法器、乘法器、双向三态门和总线等)电路结构和性能作为最基础的知识是必须了解和掌握的。
下面对一些组合逻辑部件的基础内容进行进一步的阐述。
6.1 加法器
本科学习的数字电路课程中曾对加法器进行了详细的原理讲解,加法电路即全加器,电路结构主要由与门和非门构成。其逻辑表达式为:
Ci = XiYi + Yi Ci-1 + XiCi-1
Si = Xi C i ˉ \bar{C~i~} C i ˉ + Yi C i ˉ \bar{C~i~} C i ˉ + Ci-1 C i ˉ \bar{C~i~} C i ˉ + XiYiCi-1
全加器和Si也可以表达为:
Si = Pi ⨁ \bigoplus ⨁ Ci 其中 Pi = Xi ⨁ \bigoplus ⨁ Yi
Ci = Pi ⋅ \cdotp ⋅ Ci-1 + Gi 其中 Gi= Xi ⋅ \cdotp ⋅ Yi (6.1)
其中(6.1)也就是进位递推公式。
式中Xi, Yi 表示两个加数,Si表示和,Ci-1表示来自低位的进位,Ci表示向高位的进位。
真值表如下:
表1 一位全加器的真值表
| Xi | Yi | Ci-1 | Si | Ci |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
而在日常的工作和学习中常用到的是多位数字量的减法运算,因此需要用到并行加法器,现在常用的是超前进位加法器(Carry-Look-Ahead-Adder加法器),也就是在几个全加器的基础上增加了一个超前进位形成逻辑,以减少由于逐位进位信号的传递所造成的延迟。
下图展示了一个4位二进制超前进位加法电路
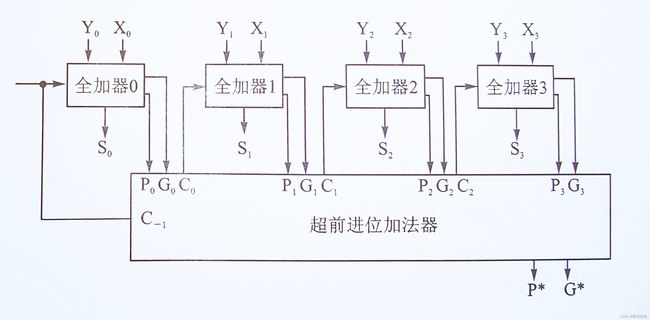
类似的16位的二进制超前进位加法器电路可用4个4位二进制超前进位加法电路再加上超前进位形成逻辑来构成,32位、64位以此类推。
以上就是关于加法器的一些基础理论知识。
超前进位形成逻辑虽然能够减少延迟,但还是有多级门和布线的延迟,而且随着位数的增加延迟还会积累,在使用加法器时,由于电路存在延迟,因此我们需要保证计算的节拍(即时钟)必须要大于运算电路的延迟,为了加快计算的节拍,常采用在运算电路的组合逻辑中加入多个寄存器组来暂存中间的结果值,即采用数字逻辑设计中常用的流水线(pipe-line)办法。
而在Verilog设计中,加法器的描述只需要把运算表达式写出来就可以。
eg:X位加法器
module add_X {
input [X-1:0] a,
input [X-1:0] b,
output [X-1:0] sum,
output C
}
assign {C,sum}= a + b; //在行为仿真时,该加法器没有延迟
endmodule
利用综合器可以对以上的代码自动综合成典型的加法器电路结构,下图展示了一个24位加法器的RTL视图:
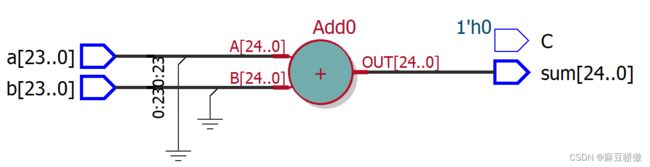
6.2 乘法器
下面简单对乘法器的基础理论知识进行讲解,以下以两个4位二进制数X和Y相乘为例进行介绍。
在对两数进行乘法运算时,需要将两数的每一位分别对应相乘然后相加,如下:

总所周知,两个一位二进制数相乘遵循如下规则:
0×0=0, 0×1=0, 1×0=0, 1×1=1
即YiXj可以用一个与门实现,记为Pi.j=YiXj
快速乘法器常采用网格形式的叠带阵列节奏,如下图所示,图中MU表示乘法单元,由一个与门和一个全加器组成,在结构上与上图的计算列式相同。其中第一行的每个MU因为没有进位,因此可以用一个与门实现;每一行的最右边一个MU中的全加器可以使用半加器代替。
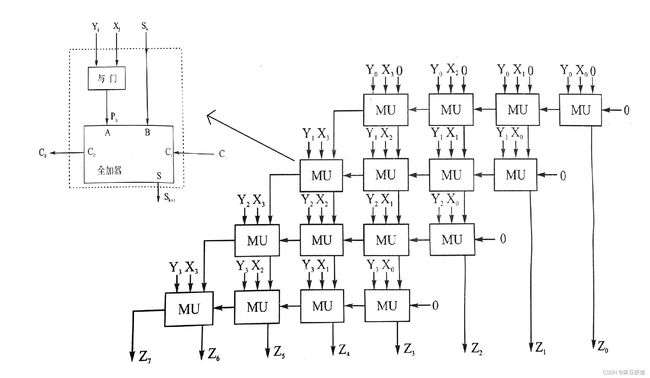
在延时方面,每个全加器的与相可以同时执行,但是下一个全加器需要上一个全加器的进位输入,因此上图所展示的乘法最长的延时为1个与门的传输延时和8个全加器的传输延时。
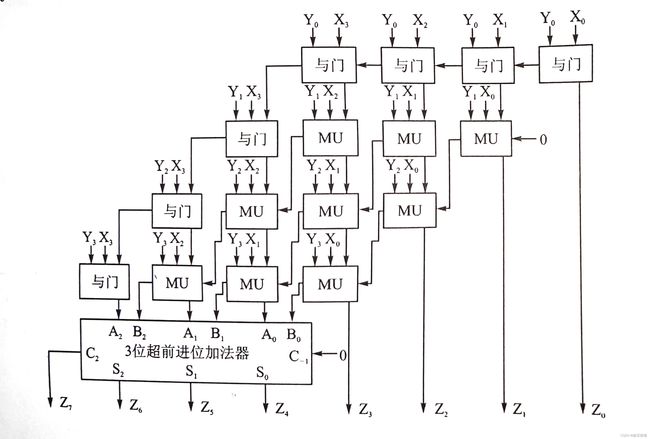
为了进一步提高运算速度,上面的乘法器可以改用进位节省乘法器(Carry-Save Multiplier),如下图所示,即在乘法器中使用一个3位的超前进位加法器。则传输延时变为1个与门的传输延时加上3个全加器的传输延时。
同样的,用Verliog来描述乘法器只需要把运算表达其写出来就可以了。
module mult_X(
input [X-1:0] X,
input [X-1:0] Y,
output [2X-1:0] Pruduct // 2个N位二进制数相乘结果位2N位
);
assign = x*Y;
endmodule
6.3 比较器
在计算逻辑中,比较数值大小也是一种常用的逻辑电路,其中一位二进制数的比较是该逻辑的基础,下表展示了一位二进制数比较电路的真值表。
| X Y | (X>Y) | (X>=Y) | (X=Y) | (X<=Y) | (X| (X!=Y) |
|
|---|---|---|---|---|---|---|
| 0 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 1 | 0 | 1 | 1 | 1 | 0 | 0 |
根据真值表可以得出一位二进制数比较电路的布尔表达式:
(X>Y) = X · (~Y)
(X (X=Y) = (~X) · (~Y) + X · Y 通常在电路设计中,比较电路常用来比较多位二进制数,位数较多的比较电路较为复杂,以前常用74LS85型四位数字比较器来构成位数较多的二进制数比较电路,如8、16、24、32位的比较器。 但在Verilog中,比较器的实现很简单,常用if语句来实现该功能,具体代码如下: 先这样,后面继续补充。。。。位数为width的2个二进制数进行比较
module compare_n(
input [width-1:0] X,
input [width-1:0] Y,
output reg XGY,
output reg XSY,
output reg XEY,
);
parameter width = 8;
always @ (X or Y)begin //每当X或Y变化时
if(X == Y)
XEY = 1; //设置X等于Y的信号为1
else
XEY = 0;
if(X>Y)
XGY = 1; //设置X大于Y的信号为1
else
XGY = 0;
if(X<Y)
XSY = 1; //设置X小于Y的信号为1
else
XSY = 0;
end
endmodule