计算机发展历史简述及CPU构成及工作过程——Crash Course内容整理
文章目录
- 0. 写在前面
- 1. 计算设备发展简史
-
- 1.1 计算设备早期
- 1.2 机械式计算设备
-
- 步进计算机
- 差分机和分析机
- 1.3 机电式计算设备
-
- 机电式穿孔制表机
- Harvard Mark I
- 1.4 电子计算机
-
- 1.4.1 真空管(Vacuum Tubes)
-
- “巨人计算机Colossus Mark I”——基于真空管的计算机
- ENIAC
- 1.4.2 三极管(Transistor)
-
- 基于三极管的计算机——IBM 608
- 2. 计算机的“思维模式”
-
- 2.1 二进制和布尔运算
- 2.2 逻辑门及组合逻辑电路
- 3. CPU组成成分及各部分介绍
-
- 3.1 ALU
- 3.2 寄存器和RAM
- 3.3 控制单元(Control Unit)和时钟
- 3.4 CPU整体结构图及工作流程
- 3.5 进阶CPU设计思想——5种方法
- 个人反思?
- 参考
0. 写在前面
之前逛B站的时候突然发现crash course系列的课程,每节课接近10多分钟,但‘单位时间内的信息量’实在是爆炸,这一些列有经济学,物理学,计算机,工程学,心理学等等,没有你想不到的。听了计算机系列的前10节(主要是硬件原理部分),感觉我对电脑的认知已经有时间顺序了,但还得自我总结一下。想想自己大四学计算机实时操作系统的时候真的全程懵逼(说的跟学数电的时候不懵似的),当时要会用B站学习…
1. 计算设备发展简史
1.1 计算设备早期
个人认为学什么课程都得追本溯源,否则无法真正理解那些概念。首先第一个问题就是“到底为什么要发明计算机?”(“方便啊!”,dbq,请不要回答这些,不具体也缺乏深度)我个人的回答是,计算机是人类社会发展到一定阶段的必然产物,首先要明确一点,人脑的纯计算速度是有限的,想想我们的计算速度吧,先拿纸拿笔,或者Ipad触屏笔,再一步步推导…;正是因为我们的大脑是有限的,并且不断增长的人类社会规模又大于我们大脑能够计算的限度,这种举步维艰的情况下我们就不得不需要能够辅助我们甚至直接帮我们计算的工具;假设人口普查每10年进行一次,不借助任何计算设备可能会花7到8年,数据早就过时了,政府也就没法合理分配资源。
以上问题弄清楚了之后我们就需要了解计算机的发展史了,也就是 “计算机(Computer)是怎么演变的?”
计算机的前身肯定是一些辅助计算设备了,比如说用来算账的算盘(Abacus);用于计算纬度的星盘(Astrolabe);甚至是时间计量工具——时钟。当这些设备不足以满足我们的需求的时候,就需要大型计算设备——Computer。
1.2 机械式计算设备
先来明确一下Computer这个单词的指代变化。最早在1613年Richard Braithwait的书中提到了computer,那时候该词是指专门负责计算的人,是一种职业名称,直到1800年还存在。在那之后computer才多被用来指代计算设备。
“ I have read the truest computer of times, and the best arithmetician that ever breathed, and he reduceth thy days into a short number.”
————Richard Braithwait
很容易想到,最早的计算设备一定是机械式的,因为那会真空管和三极管,MOSFET等等并没有被发明出来。(下一节电子计算机中会阐述)
步进计算机
最有名的机械计算设备是1694年德国科学家Gottfried Leibniz的步进计算机Step Reckoner,有点像机械式的行程计数器,每一个数位上的齿轮上有10个齿(0-9),转到9之后都会清零,然后向前进一位。它是第一台能够实现加减乘除的计算设备。但是它的速度还是太慢了,遇到大型计算的时候,人们更倾向于用 事先计算好的表格(Pre-computed table) 辅助计算(战争中计算炮弹的轨迹)。
差分机和分析机
1822年英国数学家Charles Babbage设计了差分机(Difference Machine),并做出了机器的一部分,差分机可以用来近似多项式,从而可以近似三角函数和对数的值(通过泰勒级数),还可以用于物理学中(估算射程和空气压力等)。之后Babbage又构思出了跨时代的机器,“分析机(Analytical Machine)”,这台机器相当于通用计算机(General-Purpose Computer),1) 它可以多次计算;2) 给定数据,可以按顺序执行操作;3) 也有内存和简单原始的打印机。(这让我想起了卷福演的那部阿兰图灵的传记电影《模仿游戏》Cool!)1991年伦敦科学博物馆为纪念Babbage制作了完整的差分机。英国女数学家Ada Lovelace也曾为分析机写过程序,她也被认为是第一位程序员programmer。

1.3 机电式计算设备
机电式穿孔制表机
1890年,Herman Hollerith发明了打孔制表机(Tabulating Machine),以应对美国的人口普查的极度低效事件。制表机继续沿用步进计算机的机械齿轮,但用供电设备连接其他部分。该机器中的打孔卡片(Punched Cards)非常重要,这些卡片上的孔可以代表一些数据,比如人口普查中的个人的婚姻状态等个人信息。当这些卡片被打孔之后,电路在汞的作用下连通使齿轮+1。该机器的发明让人口普查的时间缩短到了两年半。再之后,Hollerith创办了制表机器公司,在1924年与其他制表机器生产商合并,成立了IBM(International Business Machine)

Harvard Mark I
1944年IBM为盟军发明了一台计算机,也就是Harvard Mark I,为了给曼哈顿计划跑模拟。它的基本组成单元是机械继电器(Mechanical Relays),总共约有3500个继电器。通电之后,继电器中的机械开关会吸附上磁铁,开关导通。但它有两个缺点:第一,机械开关臂有质量,也就意味着开关切换的速度的上限很低,几乎不可能做到瞬时切换,最多也就只能做到1秒50次切换。第二,机械本身的齿轮磨损。整体来说,Harvard Mark I 1秒能做3次加减法,6秒完成一次乘除法,三角函数这类运算耗时更多。

1.4 电子计算机
电子计算机的发展经历了两个阶段,从真空管到三极管。每一种基本单元都对应着几台有名的计算机。
1.4.1 真空管(Vacuum Tubes)
由上文所述,机械继电器存在两点缺陷,那么我们需要找到它的替代品,幸运的是早在1904年,John Ambrose Fleming就发明了热电子管(Thermionic Valve),也就是真空管。当时的真空管价格极其昂贵,直到1940年左右价格才降到政府可以出资购买的程度。真空管的一极可以发射电子,该作用称为热电子发射(Thermionic Emission),另一极只要是正极就可以接收这些电子了。有没有发现这个现象很熟悉?这类似于二极管啊,电流是单向流通的!两年之后,1906年,美国科学家Lee de Forest在真空管的基础上加入了可控电极,将真空管改成了一个类似于开关的元器件,但与继电器不同,真空管内没有机械式组件,它可以完成1秒内几千次切换。
“巨人计算机Colossus Mark I”——基于真空管的计算机
“巨人计算机一号”是第一台大规模使用真空管的计算机,由 Tommy Flowers 于1943年12月发明,用于破解纳粹通信密码。而在两年前,也正是伟大的阿兰图灵设计了机器“Bombe”破解了恩尼格玛机(‘卷福’再次上线!)。巨人计算机用到了1600个真空管,并且总共制造了10台巨人计算机。该计算机可以说是第一台可编程的电子计算机,但编程工程量非常重,通过将线插在电线板上来完成操作。
ENIAC
ENIAC是Electronic Numerical Integrator And Calculator的缩写,1946年它由John Mauchly 和J. Presper Eckert发明于宾夕法尼亚大学。它是第一台通用的可编程的电子计算机。它1秒内可以完成5000次加法或减法,但是真空管的故障次数还是太多了,几乎没半天就会出现一次故障。尽管于1955年美国“SAGE”防空计算机系统制造了AN/FSQ-7计算机,但基于真空管的计算机的命运已经走到了尽头了。

1.4.2 三极管(Transistor)
1947年,三极管诞生于贝尔实验室,由John Bardeen, Walter Braintain, William Shockley这三位科学家发明。三极管中的Gate极控制三极管是否导通或关断,(详细理论的还是得参考模电的书)最高可以实现每秒10000次的开关切换,并且,三极管的尺寸远远小于真空管,如今计算机中的三极管的尺寸已经可以小于50纳米了。
基于三极管的计算机——IBM 608
1957年,IBM公司生产了第一台基于三极管的商用计算机。它用到了3000个三极管,可以每秒4500次加减法,80次乘法或除法等等。慢慢地,IBM公司将其他设备也都换成了基于三极管的。
2. 计算机的“思维模式”
前文中的计算机演变史中最重要的其实是开关的演变,也就是从机电式继电器,到真空管,再到现代的三极管的转变。开关的两种状态也反应了计算机的逻辑,也就是二进制。
2.1 二进制和布尔运算
用二进制或者用十进制计数是没有本质区别的。与人类由自己的十个指头发明出十进制计数类似,开关的两种状态也说明使用二进制是合适的。尽管之后的三极管能够表示出多种状态,但二进制的两个优点是很明显的,第一,二进制有利于分辨复杂的合成信号;第二,数学上的布尔代数提供了很多理论基础,比如布尔运算等,有效降低开发成本。布尔代数系统是由英国数学家George Boole于1854年发明的,这套规则明确了我们如何用符号进行语言的推理,比如说将某一三段论表示成简单的符号逻辑形式,正逻辑下正确代表1,错误代表0,然后再根据。
基本的布尔运算有三种:与、或、非(NOT, AND, OR),三种逻辑运算都可以转化为二进制的运算,二进制的0代表“False”,1代表“True”,其布尔代数表达式为: Z = X ′ Z=X' Z=X′。AND运算的真值表如下:只有两个输入都为1的时候输出才为1,只要一个是0输出一直是0。其布尔代数表达式为: Z = X ⋅ Y Z=X \cdot Y Z=X⋅Y
| 输入 | 输出 |
|---|---|
| 00 | 0 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
OR运算的真值表如下:只有输入都为0的时候输出才为0,只要输入有一个1,那么输出就为1。 其布尔代数表达式为: Z = X + Y Z=X+Y Z=X+Y
| 输入 | 输出 |
|---|---|
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 1 |
这三种布尔运算也构成了最基本的逻辑电路(下一节有详细说明)。
还要补充一下计算机是怎么存储数据的。首先明确一下二进制的单位,一1个二进制位被称为 1 bit;8个二进制位被称为1个字节Byte;二进制单位的转换如下:
1 Byte = 1 bit 1 \ \text{Byte}=1 \ \text{bit} 1 Byte=1 bit 1 KB = 1024 B 1 \ \text{KB}=1024 \ \text{B} 1 KB=1024 B 1 MB = 1024 KB 1 \ \text{MB}=1024 \ \text{KB} 1 MB=1024 KB
这里的大写字母B是指字节(Byte)
计算机表示数字
计算机在表示整数的时候用第一位来表示数的正负,比如用32bit表示有符号数字的范围是: − 2 31 ∼ 2 31 − 1 -2^{31}\sim2^{31}-1 −231∼231−1;计算机表示浮点数的一种方法是IEEE-754标准,即先将某浮点数转化为二进制浮点数,再将该数转化为科学计数法形式,最后用32位存储器存储数据,其中第1位表示符号位,接下来的8位用来存储指数位,最后的23位表示有效数位。
计算机表示字母,或字符
ASCII码用7个二进制位表示共128个字符,其中囊括了大小写的英文字母表,标点符号一些指令码,比如转义字符等。但是ASCII的局限在于它只适用于英文的编码。最后国际上统一用Unicode的编码形式,16个二进制位来编码各国语言。其他数据比如图片,音频,视频都是二进制编码的。
2.2 逻辑门及组合逻辑电路
首先按抽象层次从高到低的顺序理一下。组合逻辑电路是由一个个逻辑门组合而成,而一个个逻辑门又是由晶体管组成,组合逻辑电路可以用来构成我们电脑中的CPU,存储器等(进一步的抽象)。所以本节内容按抽象层次从低到高展开。最底层的是三极管,本科阶段模电学的就是BJT和MOSFET了。(当时真是学到快崩溃,不知道学这些有啥用) BJT和MOSFET的示意图如下图所示。

这里以BJT为例,构造一个简单的非门,如下图。
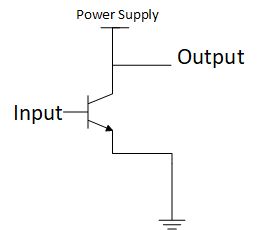
输入为0时,输出为1(输入为0的时候三极管没有导通,这时候电源的电流直接流向输出端);输入为1的时候,输出为0。(接地之后电流直接流向地)
如果把三极管的符号用开关符号替换掉,那么用三极管构造与门和或门是非常容易的,即与门是开关的串联;或门是开关的并联,见下图的简易模型。
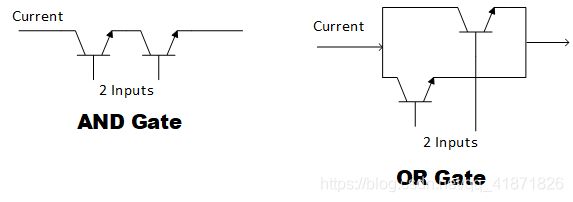
有了底层的结构,我们就可以省去把每个门电路都表示成一个个三极管的功夫,进行下一层的抽象了,三个基本门电路外加一个常用的XOR电路如下图所示。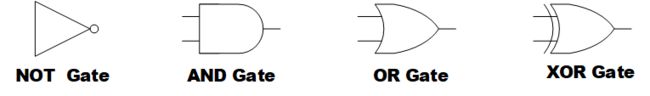
其实XOR门电路是一种简单的组合电路, 因为常用就用特殊符号将其抽象了出来。它内部的逻辑可以用以下电路表示。
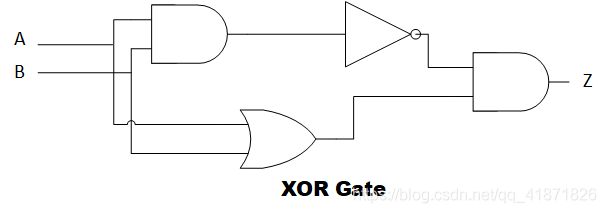
3. CPU组成成分及各部分介绍
组合逻辑电路构成了CPU的各个模块。CPU的模块有ALU(Arithmetic Logic Unit算术逻辑单元)、寄存器Registers、Cache(高速缓存)和RAM(Random Access Memory)、和控制单元。
3.1 ALU
ALU的功能是进行数值和逻辑运算,其中数值运算包括加减法和增量运算(之前的ALU很少有内嵌乘除法的,大部分都用加减法代替乘除法);逻辑运算则包括检测输入的数字是否为0,是否有溢出(Overflow)等。最著名的ALU是Intel 74181,第一个将ALU集成在单一芯片上,它总共可以处理4-bit输入,约有70个逻辑门。
本段以加法器(半加器和全加器)为例介绍组合逻辑电路是如何组成ALU的。两个1-bit二进制数的加法(半加器)真值表如下,表中包括了进位和末位,可以看出进位的输出等效于与门,末位的逻辑等同于异或门。
| A | B | Carry | Sum |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
半加器的逻辑电路图如下,就是简单的与门和异或门的组合,知道了具体的逻辑电路之后进行下一层的抽象。
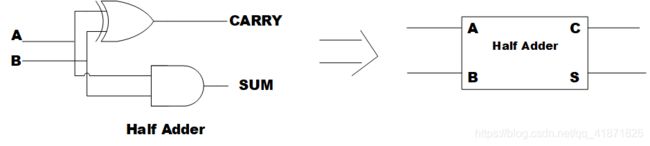
之所以称为半加器是因为在实际的多比特二进制数加法当中,一般都会产生进位(联想十进制的加法,需要加进位的值),所以完整的加法(全加器)应该是三个1-bit二进制数相加,真值表应该有 2 3 = 8 2^3=8 23=8种输出(半加器只有4种输出)。全加器的真值表如下图:
| A | B | C | Carry | Sum |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
通过半加器实现的逻辑电路图如下,之后继续进行下一层抽象:

以上只是1-bit全加器,通过嵌套更多的全加器可以得到8-bit加法器,甚至是n-bit,这里我就直接附上视频课程的截图了,如果所加的数超出了8-bit加法器的极限(255),那么就会发生溢出(Overflow)现象。

上图所示的加法器结果被称为行波进位加法器(Ripple Carry Adder)。更现代的加法器是超前进位加法器(Csarry-look-ahead Adder)
最后一步,将上述的元器件再进行一次抽象,得到“V”型ALU逻辑符号,如下图所示。其中Flags是标志位,常见的有溢出位,0标志位,负标志位(有助于逻辑判断)。
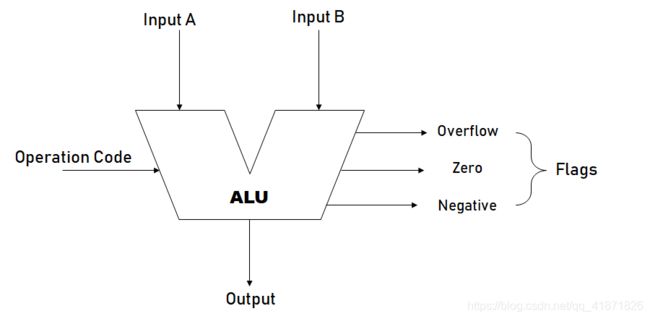
3.2 寄存器和RAM
ALU实现了运算功能,但除此之外,有些数据是需要保存的,比如说我们在用电脑的时候第二次打开同一个程序的时候速度非常快,这就是因为RAM的保存了一些程序的数据,以方便用户二次使用。寄存器和RAM都是存储器,只不过RAM包含了很多的寄存器,抽象层级比寄存器高一级。RAM,即随机访问存储,也就是我们常说的内存条,它在不断电的时候会存储信息。现在的台式机常见的内存条至少也是8GB(比特数是 8 × 102 4 3 × 8 bit 8\times1024^3\times8 \ \text{bit} 8×10243×8 bit)。本节还是从“最底层”,存储1-bit信息的逻辑电路讲起。
存储电路和上文中的逻辑电路不大一样,存储电路需要将输出信息返回到输入端。从最简单的存储0的电路则是将与门的输出接回输入,而存储1的电路是将或门电路的输出接回到输入,如下图:
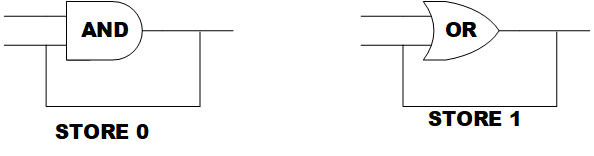
对与门来说,当输入至少有1个0的时候,输出就保持0不变;对或门来说,输入至少有1个1的时候输出保持1不变。将这两种电路组合在一起,就构成了存储1-bit的电路,叫做“与-或锁(And-Or Latch)”,逻辑电路如下,术语中用了“锁”非常形象,相当于把信息锁住了。第一种情况是当set位为1,reset位为0的时候,输出被设置为1;第二种情况是当set为1,reset也为1的时候,输出被设置为0(reset为0,与门的输出必为0);第三种情况是set和reset都为0,这时候输入并不影响输出,所以输出就与上一个时刻的输出保持一致,信息被锁住了!

平时在写入(存储)数据的时候大部分情况不会向上图那样使用set和reset,而是使用数据输入线和写入使能(Write Enable)两条线,当写入被使能之后,才能进行数据写入,只需要对上图的逻辑电路图稍作改动即可,逻辑图如下,此电路被称为门锁(Gated Latch)(可以形象地想象成 )。

寄存器
寄存器是一组含锁存器的模块(里面还含有一些简单门电路,三极管),能够存储的比特数被称为带宽。例如,如果想要存储8位的数据量,最简单的办法就是按顺序依次排列这些锁存器。但是,这种排列方式有个缺点就是所需要的线太多,现如今的寄存器都是以字节为基本单位的,n-bit的寄存器(也就是n个锁存器的顺序排列)需要 2 n + 1 2n+1 2n+1条线,这其中有n条数据输入线,n条数据输出线和1条写入使能线。为了克服这一点,我们选择将n个锁存器按照矩阵模式排列,比如256-bit的寄存器中的锁存器就是按照 16 × 16 16\times 16 16×16来排列的,每行每列都可以用4条线(4-bit二进制数),总共也就是8条地址线(8-bit二进制数)。下图用16-bit寄存器做示意图,这里的Data线是双向的,既可以读取又可以写入。
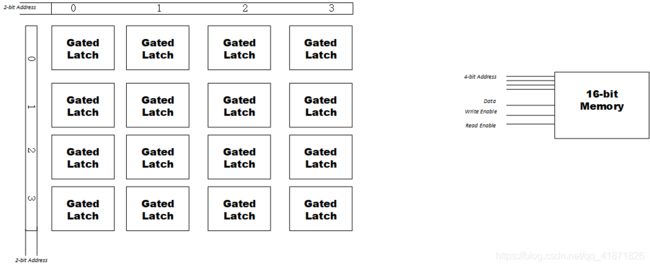
将这一层的抽象再排列起来,就组成了RAM,如下图所示,地址线可以到 2 8 = 256 2^8=256 28=256条,而每一条地址可以访问8-bit的数据(由4-bit操作码和数据地址或寄存器地址),可以自行计算一下这块RAM的大小。

3.3 控制单元(Control Unit)和时钟
CPU中还有个非常重要的成分就是控制单元。控制单元中用于解码指令(比如说每一个操作码代表什么样的操作或运算,指向的是哪一块内存中的数据等),使能读取数据或写入数据;除此之外,控制单元中还有指令地址寄存器(存指令所在的地址)和指令寄存器(以二进制数编码的指令),另外,还有能够显示ALU标志位的一些逻辑电路(见前文ALU部分)。
3.4 CPU整体结构图及工作流程
前面三节详细介绍了CPU的一些重要组成部分,这一节内容将整合前三节的内容,并阐述CPU工作的每个阶段。
直接用视频的截图来展示CPU的整体结构,如下图所示。(当然这只是通过比较高层次的抽象来看待CPU,具体电路肯定不是这样的。)
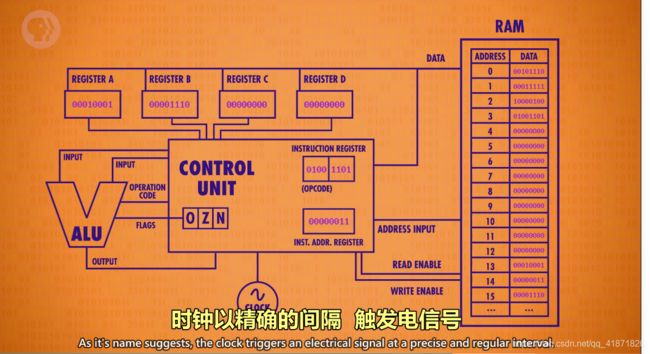
CPU工作流程
有了CPU的整体结构,接下来就是了解CPU是怎么工作的了。先明确指令集表,这里就简单的用4条指令作为demo了。
| 指令 | 描述 | 4位操作码 | 地址或寄存器 |
|---|---|---|---|
| LOAD_A | 将RAM地址中的数据写入寄存器A | 0010 | 4位RAM地址 |
| LOAD_B | 将RAM地址中的数据写入寄存器B | 0001 | 4位RAM地址 |
| STORE_A | 将寄存器A中的数据写入RAM地址中 | 0100 | 4位RAM地址 |
| ADD | 将两个寄存器中的值相加,并存入第二个寄存器中 | 1000 | 2位寄存器ID;2位寄存器ID |
有了这个最基本的指令集,CPU就会按照取指令,解码和执行指令这三个阶段开始工作。 在取指令的阶段,指令地址寄存器会访问RAM存储指令的地方,并将指令存放到指令寄存器中;解码阶段由控制单元内部的一些逻辑门电路完成,告诉ALU具体是哪条指令。在之后的执行阶段中,控制单元会访问RAM中相对应的数据位置,并将数据写入到对应的寄存器中。**最后,要注意!将指令地址寄存器中的数据加1。**整个工作周期由时钟频率决定(Clock Speed),时钟频率越快,单位时间内CPU能够处理的指令越多,计算机工作速度越快。
以上的工作流程涉及到的指令非常简单,只是存,写,加。当然指令不止这些,还可以设计指令来改变指令的执行顺序(JUMP),还可以通过加一些判定条件来决定是否改变指令顺序(比如JUMP_NEG就是如果某个数为负数,则进行程序跳转)以实现循环,如果要进行有限循环,则需要终止程序(HALT),而无限循环则不需要。另外,先进的CPU中指令的长度是可以改变的,像HALT这类指令的长度不需要那么长,指令长度超过所需要的长度就是一种信息冗余的状态。
3.5 进阶CPU设计思想——5种方法
现如今的CPU的时钟频率都是GHZ级别的,单位时间内处理的指令太多了。但人类总是贪婪的,还在思考如何将CPU设计的更快。第一种方法是缩短三极管的开关切换时间,也就是增加开关的频率,但是该数值会达到一定上限,所以这条方案并不可行。进行第二种方法之前要明确CPU和RAM是分开的, 尽管电子传输的速度接近光速,但在超高的时钟频率下也是会由延迟的,所以这时候我们使用一些技巧,在CPU中添加Cache(高速缓存模块),将RAM中一部分的数据存放到cache中来以增加CPU的读取数据的速度。高速缓存的大小一般是KB~MB之间,如果CPU所请求的数据在cache中已经存在了,这就被称为Cache Hit(命中!),反之,数据不在cache中责备称为Cache Miss。CPU会直接更改cache中的数据然后重新放回到RAM中去,但是这时候会出现cache中的所拷贝的数据和RAM数据不同步的问题。要解决这个问题,我们就需要记录这些变化,在cache中的每一块数据中做好特殊标记,被称为“脏位Dirty Bit”,在进行同步的时候,CPU首先检测脏位,如果是脏的(If it is dirty),则cache会将自身的数据写入RAM并擦除之前的数据以释放空间,接下来才是copy新的数据块。第三种方法是指令流水线(Instruction Pipelines),示意图如下:
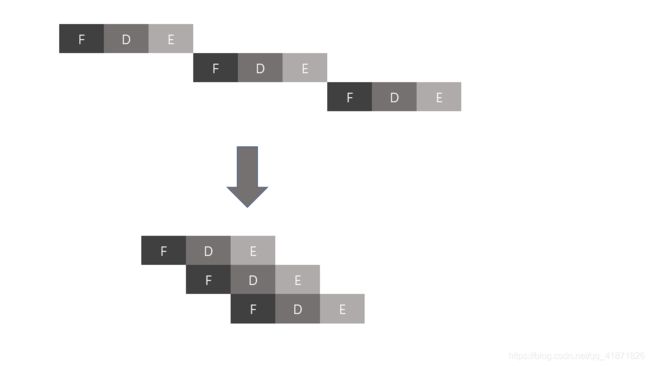
可以明显看出,图中下端的CPU工作速度是上方的三倍(吞吐量*3)但要注意,进行流水线的时候会遇到如下几个问题,第一,要关注数据或者是指令之间的相关性 data dependencies(比如,CPU想要取某个指令,但是这条指令这时正在被修改,会造成不同步的问题,与上文的cache也有异曲同工之处),流水线需要提前预测这些相关性,否则将停止流水线工作 (Stall the pipelines)。高端处理器会动态规划这些相关的指令以最小化停工时间(Minimize the stalls),这也叫做乱序执行(Out-of-order Execution)。第二,问题会出现在条件跳转中,一旦JUMP出现,流水线会暂停工作,但是这会造成空等(idle wait),降低了效率。因此,高端CPU会推测JUMP会到哪条指令中,这种行为被称为推测执行(Speculative Execution)。如果CPU预测错了,就会清空流水线中的所有内容(Pipeline Flush),这也是第三个问题。为解决这个问题,高端CPU提出了分支预测的方法(Branch Prediction)。第四种加快CPU速度的方法是超标量处理器(Superscalar),它可以在一个时钟周期内完成多条指令。这种处理器再进一步榨取各个元器件的产出效率,比如取指令的时候ALU是空闲状态,或者是在一个CPU中同时让多个ALU工作。真是丧心病狂啊哈哈!示意图如下:
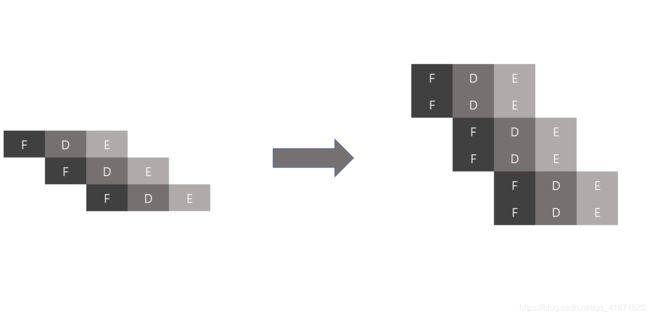
以上四种方法都是优化一个CPU的工作效率(吞吐量?),第五种方法则是利用多核处理器(Multi-core Processor),在一个CPU内设计多个独立的处理单元,它们之间会共享一些资源,比如RAM,寄存器,cache等内存模块等。
最后要吹一下中国的超级计算机了,“坐落于”中国无锡的超级计算机——神威,太湖之光!它有40960个CPU,每一个都是256核的,频率在1.45GHZ,运算速度可以达到每秒9.3亿亿次浮点数运算(FLOPS),真的强!
个人反思?
本段可以直接跳过,只是写博客之前的情绪酝酿,放在文末为了不耽误正文内容。
想想自己上次更新博客还是在6.20号的那篇关于多变量微积分的,多变量微积分的最后一章在这两天之内会完成,快一个月没有自我输出了,之前的毕业活动确实激发了自己不少的感性神经,想起了这四年的起伏。毕业活动还是有点耽误计划的,不过也算放了个小假轻松一下,最近正在恢复个人状态中。
不得不承认在家学习的效率还是不能跟在学校图书馆比啊。昨日鼓起勇气在B站上搜索关于计划制定的方法和提高学习效率的方法,大有发现!这“番茄ToDo”真是一款超强时间管理和计划APP啊,开始写博客的这天发现自己能感知到的效率肯定翻倍了,每25分钟一个cycle还是很实用的。有的时候真后悔自己没能早点认识B站,自己还是缺点敢于搜索的勇气,还得承认一点,“不知道自己不知道”的无知状态也挺可怜的。
参考
计算机科学速成课1~10:https://www.bilibili.com/video/av21376839
差分机介绍:https://baike.baidu.com/item/差分机/9423361