朴素贝叶斯分类器原理介绍及python代码实现

目录

频率学派和贝叶斯学派

朴素贝叶斯分类器

python实现朴素贝叶斯分类器

---

频率学派和贝叶斯学派

说起概率统计，不得不提到频率学派和贝叶斯学派，通过对概率的不同理解而演变的两个不同的概率学派。

频率学派

• 核心思想：需要得到的参数​是一个确定的值，虽然未知，但是不会因为样本X的变化而变化，样本​数据随机产生的，因此在数据样本无限大时，其计算出来的频率即为概率。其重点主要在于研究样本空间，分析样本X​的分布

• 延展应用：最大似然估计（MLE）

贝叶斯学派

• 核心思想：需要得到的参数​是随机变量，而样本​则是固定的，其重点主要在于研究参数​​的分布。 

  由于在贝叶斯学派中参数​​的是随机变量，是随着样本信息而变化的，所以贝叶斯学派提出了一个思考问题的固定模式:先验分布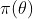+样本信息->后验分布​。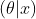 

• 延展应用：最大后验估计（MAP）

• 贝叶斯公式

  假设A的先验概率为P(A)，B的先验概率为P(B)，B发生的条件下A发生的后验概率为P(A|B)，A发生的条件下B发生的后验概率为P(B|A)，则有

化简可得：

其中A表示一种预测结果；B表示一组观测数据；P(A)表示A的先验概率，即在未观测到B之前A的概率；P(A|B)表示A的后验概率，即在观测到B之后A的概率；P(B|A)为似然函数(likelihood)；P(B)为证据因子(model evidence)

该公式可以理解为后验概率=先验概率调整因子​，在上式中，后验概率为​P(A|B)，先验概率为​P(A)，调整因子为​

朴素贝叶斯分类器

基于贝叶斯定理，延伸出了一个异常朴素的分类算法--朴素贝叶斯分类器，其基本思想为：在给定条件下，计算各可能类别的概率，取最大极为预测值。从上述思想可以确切的明白，朴素贝叶斯适用于离散数据，下面将给出其数学描述。

设​为输入，​为x​的特征属性，假设其特征属性都是相互独立的，需要预测​x是​中的哪一类

根据贝叶斯分分类器的思想，应该为概率最大的类别，即如果​，则有​，根据贝叶斯定理，每个类别的概率为：

可以发现其分母与i无关，因此可以仅通过分子来比较不同类别的概率。

python实现朴素贝叶斯分类器

import pandas as pd
 ​
 def load_data(path,sep=',',encoding='utf=8'):
     '''读取数据，输入数据需要有表头
     return dataframe'''
     filetype = path.split('.')[-1]
     if filetype in ['csv', 'txt']:
         data = pd.read_csv(path, sep=sep, encoding=encoding)
     if filetype == 'xslx':
         data = pd.read_excel(path)
     return data
 ​
 ​
 def cal_prob(data,col,res):
     '''计算出现频率'''
     count_all = len(data[col])
     count_res = len(data[data[col]==res])
 ​
     return count_res/count_all
 ​
 ​
 def cal_prio_prob(data, label):
     '''计算先验概率
     return {res1:prob1, res2:prob2,...}'''
     prio_prob = {}
     for res in data[label].unique():
         prob = cal_prob(data, label, res)
         prio_prob[res] = prob
     
     return prio_prob
 ​
 ​
 def cal_likelihood_prob(data, label, input):
     '''计算似然函数
     return {res1:prob1, res2:prob2,...}'''
     likelihood_prob = {}
     for res in data[label].unique():
         data_p = data[data[label]==res]
         prob = 1
         for col in data:
             if col != label:
                 prob = prob * cal_prob(data_p, col, input[col])
         likelihood_prob[res] = prob
     
     return likelihood_prob
 ​
 ​
 def bayes_classifier(path, label, input):
     '''比较输出最可能的类别'''
     data = load_data(path)
     prio_prob = cal_prio_prob(data, label)
     likelihood_prob = cal_likelihood_prob(data, label, input)
     max = 0
     for c in prio_prob.keys():
         prob = prio_prob[c] * likelihood_prob[c]
         print(f'{c}的结果为{prob}')
         if prob > max:
             cla = c
             max = prob
     
     print(f'在{input}情况下，{label}的结果为{cla}')
     
     
 if __name__=='__main__':
     path = 'weather.csv'
     label = 'PlayTennis'
     input = {'Outlook':'Sunny', 'Temperature':'Cool','Humidity':'High','Wind':'Strong'}
     bayes_classifier(path, label, input)

稍微改进了一下，封装成接口，代码如下：

import pandas as pd


class naiveBayesClassfier():
    '''贝叶斯分类器
    fit: 训练分类器
    predict：预测分类结果'''
    def __init__(self, data, label):
        # 特征
        self.features = [x for x in data.columns.tolist() if x!=label]
        # 结果分类
        self.res = data[label].unique()
        # 先验概率
        self.prio_prob = {}
        # 似然函数
        self.liklihood_prob = {}
        # 证据因子
        self.evidence_prob = {}

    def fit(self, data, label):
        '''训练朴素贝叶斯分类器
        - data: 输入数据
        - label: 预测值
        return: 概率 '''
        row, _ = data.shape
        # 先验概率
        for i, j in data[label].value_counts().to_dict().items():
            self.prio_prob[i] = j/row
        # 似然函数
        for l in data[label].unique():
            data_n = data[data[label]==l]
            row_n, _ = data_n.shape
            prob2 = {}
            for col in self.features:
                prob1 = {}
                for i, j in data_n[col].value_counts().to_dict().items():
                    prob1[i] = j/row_n
                prob2[col] = prob1
            self.liklihood_prob[l] = prob2
        # 证据因子
        for col in self.features:
            prob3 = {}
            for i, j in data[col].value_counts().to_dict().items():
                prob3[i] = j/row
            self.evidence_prob[col] = prob3

    def cal_prob(self, input, res):
        '''计算似然概率，证据因子'''
        liklihood = 1
        evidence = 1
        for col in input.keys():
            print(col)
            v = input[col]
            liklihood = liklihood * self.liklihood_prob[res][col][v]
            evidence = evidence * self.evidence_prob[col][v]

        return liklihood, evidence

    def predict(self, input):
        '''分类器预测
        - input：需要预测的数据
        return：预测的结果及概率'''
        prob = {}
        for res in self.res:
            liklihood, evidence = self.cal_prob(input, res)
            prob[res] = self.prio_prob[res]*liklihood/evidence

        print(prob)
        prediction = max(prob, key=lambda x: prob[x])
        probability = prob[prediction]
        
        return prediction, probability


# 使用
import pandas as pd
import naiveBayesClassfier

data = pd.read_csv('weather.csv')
label = 'PlayTennis'
model = naiveBayesClassfier.naiveBayesClassfier(data, label)
input = {'Outlook':'Sunny', 'Temperature':'Cool','Humidity':'High','Wind':'Strong'}
# 训练模型
model.fit(data, label)
# 预测
prediction, probability = model.predict(input)

参考贝叶斯公式由浅入深大讲解