变分自编码器VAE详解

emmmmm…先来一首BGM吧。

VAE的讲解

网络的逻辑输入和输出 这是我为了更加清晰的介绍流程图而设定的（不知专业的词哈）

   首先，对于一批数据来说，生成模型的目标就是学习得到一个分布$P(X)$，使得该分布和数据的真是分布$P_{gt}(X)$很接近，这样一来，我们就可以根据得到的$P(X)$来生成该数据集中到数据，也就是达到了生成数据的目的，这就是生成模型的最终目标。但是，我们无法直接获得这样的$P(X)$，而且，随着$X$的维度的变大，很多的方法例如蒙特卡洛近似就无法使用。既然是概率图的形式，我们可以采用如下的模型来生成$X$–通过引进一个隐层变量，这样$P(X)=\int P(X|Z)P(Z)dz$，而且我们假设$p(z)\sim N(0,1)$，$P(X|Z;\theta )=N(X|f(Z;\theta ),{\sigma }^2\ast I)$。其中$f(Z;\theta )$是网络的输出，$P(X|Z)$是网络拟合的函数。这样我们就可以用过采样得到$Z$，输入网络得到最后的$P(X)$(这就是终极目标)，再通过近似或者采样等操作生成$X$。但是这个网络太难训练了，因此直接从一个正太分布中采样$Z$输入到网络中，其对于网络拟合的$P(X)$的贡献可能为0！这样，如果$X$的维度也很高的话，网络学习的难度就更大了，因此这样的方法不符合实际。

  插播一则广告：网络的输出 和 网络的拟合函数是不一样的,而且网络最终的逻辑输出也不一样！例如我们训练一个网络来拟合高斯分布，此时，你网络的输出可能是$(\mu ,\sigma )$，但是网络最终拟合的是$P(X|Z)=N(\mu ,\sigma )$,但是此时如果$Z$也是一个随机变量的话，那么网络最终符合的逻辑输出是$P(X|Z)P(Z)$。

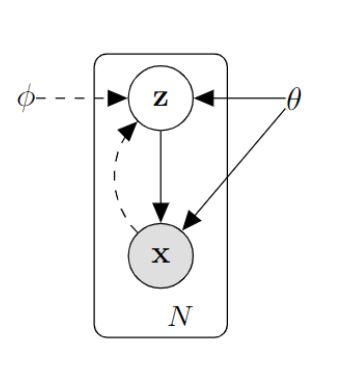
  那么，怎么改进上面的生成模型呢，还是使用隐层变量的话，这时候，我们要保证采样得到的$Z$是每个数据$X$专属的变量，它是有利于构建P(X)的，因此我们决定从P(Z|X)中采样，这样一来，$Z$是依赖于输出的$X$的，它对于重构出$X$有很高的置信度。那么此时的P(Z|X)会是什么分布呢？当然是高分布$N(0,I)$！这样，encoder的输出$(\mu ,\sigma )$就可以采用KL散度来训练。注意此时和之前的区别！！此时采样后输入到网络中的$Z$虽然是$P(Z)\sim N(0,I)$，但是这是网络的拟合输出，网络的逻辑输出是$P(Z|X)$,也就是此时的Z是采样于$P(Z|X)\sim N(0,I)$，这是有区别的！逻辑输入就不一样了。这样，网络就变成了下面的例子：

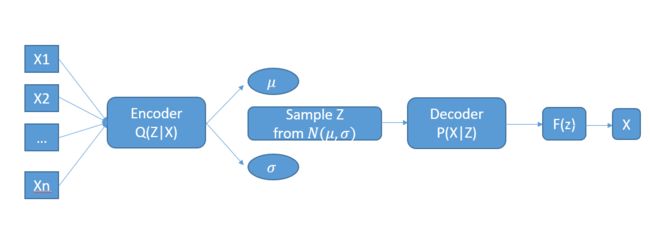
  VAE的关键是在隐层的处理，引进了$Q(Z|X)$来近似$P(Z|X)$，这样就可以通过采样$Z$,来最大化$P(X)$，$P(X)$是网络的逻辑输出。是需要最大化的目标，也就是最大似然。当 每次只进行一次采样的时候，边缘概率$P(X)\approx P(X|Z)$，因此要最大化网络拟合的函数（注意是拟合的函数，而不是输出）！！那么，引进了$Q(Z|X)$来近似$P(Z|X)$，发生了什么变化？？我们采用KL散度来度量这两者之间的关系，可以得到如下的公式：
$$D[Q(Z|X)||P(Z|X)]=\int Q(Z|X)log\frac{Q(Z|X)}{P(Z|X)}=E_{Z\sim Q(Z|X)}[logQ(Z|X)-logP(Z|X)]\text{\hspace{1em}(1)}$$
利用贝叶斯后验概率公式得到：
$$D[Q(Z|X)||P(Z|X)]=E_{Z\sim Q(Z|X)}[logQ(Z|X)-logP(X|Z)-logP(Z)]+logP(X)\text{\hspace{1em}(2)}$$
这样，我们间接得到了$P(X)$,也就是网络的逻辑输出，更是我们想要最大化的目标！，移动一下位置，得到：
$$logP(X)-D[Q(Z|X)||P(Z|X)]=E_{Z\sim Q(Z|X)}[logQ(Z|X)-logP(X|Z)-logP(Z)]\text{\hspace{1em}(3)}$$
利用KL散度的公司，最后变换得到：
$$logP(X)-D[Q(Z|X)||P(Z|X)]=E_{Z\sim Q(Z|X)}[logP(X|Z)]-D[Q(Z|X)||P(Z)]\text{\hspace{1em}(4)}$$

(4)中的$E_{Z\sim Q(Z|X)}[logP(X|Z)]$和我们之前分析的如果只采样一次的时候一样。此时网络的输出是$f(z;\theta )=\mu$,要使得$E_{Z\sim Q(Z|X)}[P(X|Z)]$最大，那么就要使得$\mu$和$X$很接近,我们假设输出是高斯分布，而且$\sigma$是手动设置很小的值，此时其表达式的对数为
$$logP(X|Z)=C-\frac{1}{2}||X-\mu |{|}^2/{\sigma }^2\text{\hspace{1em}(5)}$$
这，，，不就是重构损失吗？？？。这也太巧合了吧？（其实这里可以参考这篇文章中，阅读完你就知道为什么了。）decoder网络拟合的是$P(X|Z)$，此时该函数的变量是$X,\mu$。KaTeX parse error: \tag works only in display equations
训练的时候，X是固定的，训练得到的是$\mu$,而当用于生成的时候，$\mu$是固定的，$X$是生成的，因此，训练的时候，寻找$\mu$使得网络拟合的函数输出最大。这里主要用于区分网络拟合输出的$P(X|Z)$和最大似然的目标$P(X)$之前的关系，通过单次采样之后，整个decoder的逻辑输出是$P(X)$,此时的X是输出的数据，而不是生成的数据！而整个网络的训练不仅仅是$P(X)$这一项，因为中间拟合函数的引进，因此才有了最终的Loss函数。这样才能使得最后重构的X是符合概率分布逻辑流的。

  这里再讨论一波所谓的变分下限是什么？由(3)可知道，
$$logP(X)=E_{Z\sim Q(Z|X)}[logP(X|Z)]-D[Q(Z|X)||P(Z)]+D[Q(Z|X)||P(Z|X)]$$
而最后一项的$D[Q(Z|X)||P(Z|X)]$是非负数的，因此有
$$\mathcal{L}=E_{Z\sim Q(Z|X)}[logP(X|Z)]-D[Q(Z|X)||P(Z)]\text{\hspace{1em}(7)}$$
这一项就是传说中的变分下限，因此，最大化一个目标函数的时候，可以通过最大化其下限来实现。此时，误差项的引进就是$D[Q(Z|X)||P(Z|X)]$的省略，我们假设网络足够完美，以至于这一项的KL散度接近零。那么对于这个变分下限，我们如何进行优化呢？这一项中有一个KL散度和一个网络的拟合输出。网络的拟合输出上面分析过，可以通过一次采样近似$E_{Z\sim Q(Z|X)}[logP(X|Z)]\approx logP(X|Z)$。最大化该项，只需要调整网络的参数使得网络的输出$\mu$和X接近即可。另外一项是$D[Q(Z|X)||P(Z)]$，这里有两个函数$Q(Z|X)$和$P(Z)$，由于需要计算KL散度，因此需要明确的形式，我们假设先验概率依旧是正态分布$P(Z)\approx N(0,I\ast \sigma )$,要使得该项最小，那么我们让Q(Z|X)也向着标准的正态分布靠近，因此我们让网络拟合$N(0,I)$,也就是网络的输出$\mu \to 0,\sigma \to I$。这样确实可以使得该项的KL值变小，到这里，我们好像基本实现了变分下限的最优化分析----使得网络的重构最小，使得$D[Q(Z|X)||P(Z)]$最小。整体的流程如下：

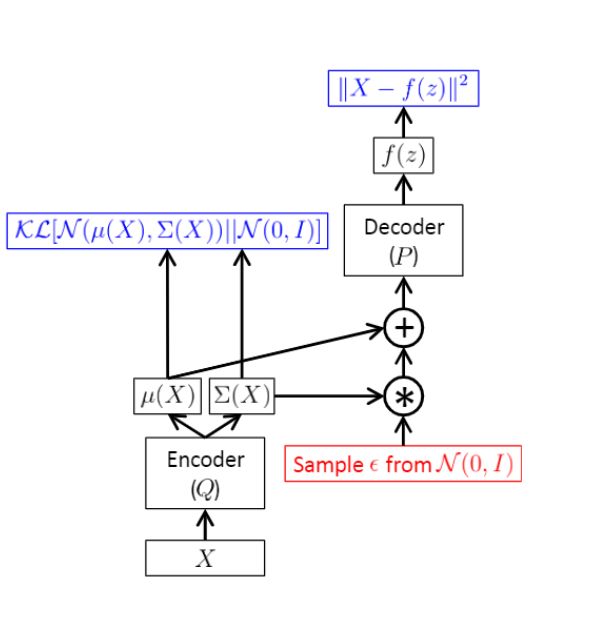
但是，还有个很重要的，那就是一开始的$D[Q(Z|X)||P(Z|X)]$，这一项被省略掉，那么后面的优化能否保证这一项也趋近于零呢？在一篇的tutorial中有推到过程：

这样，我们就可以通过优化变分下限，从而实现最终的目的了。

  变分贝叶斯主要用与解决无法计算的后验概率的情况，例如本例中的$P(X|Z)$就是无法解决的，通过近似的思想来求解（这就涉及到很多利用函数下限来不断逼近的方法，EM算法就是其中的一种方式，EM算法通过不断的更新其最大值，使得近似函数的下限不断变大最终收敛）。其实这里还有 一个启发，那就是利用网络来拟合各种棘手的函数，这是很好的，而且，通过变分下限等手段，得到最优化目标的其他的表示方式，这是一个很好的例子。

VAE生成模型以及流动逻辑

  首先要明确的是，VAE是的后半部分(decoder)是一个生成模型，因为它用于生成一些新的图像。那么生成模型是什么？？
给出维基百科的定义：在概率统计理论中, 生成模型是指能够随机生成观测数据的模型，尤其是在给定某些隐含参数的条件下。它给观测值和标注数据序列指定一个联合概率分布。在机器学习中，生成模型可以用来直接对数据建模（例如根据某个变量的概率密度函数进行数据采样），也可以用来建立变量间的条件概率分布。条件概率分布可以由生成模型根据贝叶斯定理形成。生成模型。

  在VAE中，数据在流动的时候，会将其逻辑一起流动到下一个网络中，因此网络的逻辑输出是要考虑变量的先验概率的。VAE的网络结构是

  encoder网络的输入是X,网络的拟合的是后验概率$P(Z|X)$的近似值$Q(Z|X)$，网络的输出是$(\mu ,\sigma )$这两个参数是概率分布函数的参数值。decoder的输入是$Z$，采样于$P(Z|X)$,网络的拟合的是$P(X|Z)$，网络的输出是$\mu$,而$\sigma$手动设定很小。VAE的本意是，如果直接从$P(Z)\sim N(0,1)$中采样的话，那么输入到decoder中时候，没有很高的置信度来生成合理的$X$，因此，decoder中的输入应该要充分利用观测数据$X$，也就是从$P(Z|X)$中采样，这样的所采样的$Z$具有更高的可信度来生成$X$。同时，由于网络最后拟合的逻辑是$P(X|Z)\ast P(Z)=P(X,Z)$，通过MC模拟，可以得到:$\int P(X|Z)P(Z)dz=\int P(X,Z)dz=E_{Z\sim P(Z)}[P(X|Z)]\approx \frac{1}{L}{\sum }_{i=1}^{L}P(X|Z)$最后的约等于是采用门特卡罗近似得到的。由于$Z$的取值置信度很高，
因此可以只采样一次！，也就是$L=1$(如果Z的取值使得生成X的置信度不高的话，而且X是一个很高纬度的向量，那么在采用的时候，由于维度太高，要使得每个维度的采样都基本符合真实的分布的话，需要进行巨大数量的采样才能满足，这是不现实的。).

  因此，上面的式子其实是$P(X)=P(X|Z)$,也就是说，网络最后模拟的是P(X)的近似值（因此，网络的输出肯定是要最大化的。。。。）。而且，通过假设最后输出的分布形式(伯努利分布或者是高斯分布)，最后生成真实图像的时候，不用再从$P(X)$中采样，有两个原因，一个是采样的话，直接从拟合出的$P(X|Z)\sim N({\mu }_1,{\sigma }_1)$中采样也可以，但是多增加了采样的步骤；二是，由于此时的${\sigma }_1$是手动设置很小，此时的网络输出$\mu$是高斯分布的均值，和样本$X$的分布基本重合，因此可以直接使用$\mu$来代表最终需要生成的$X$。

意义：

  这篇文章主要是讲解整个VAE的工作流程，以及个步骤为什么works，文章存在很多不合理的地方，欢迎批评指出！VAE的主要贡献是它完美将概率图和深度学习结合起来，使得深度学习称为工具而不是方法。

references

（一篇是tutorial，一篇是原文。主要还是看这2文章）

Tutorial on Variational Autoencoders

Auto-Encoding Variational Bayes

Tutorial - What is a variational autoencoder?

其他的参考文献（参考辅助）

变分自编码器VAE：原来是这么一回事 | 附开源代码

变分自编码器（Variational Auto-Encoder，VAE）

Lecture 13:Generative Models

【干货】一文读懂什么是变分自编码器

从自编码器到变分自编码器（其二）

概率图模型（PGM）有必要系统地学习一下吗？

变分自编码器的原理和程序解析

Introduction to variational autoencoders VAE第二篇

【Learning Notes】变分自编码器（Variational Auto-Encoder，VAE）

VAE(Variational Autoencoder)的原理

苏剑林‏. 变分自编码器（一）：原来是这么一回事

苏剑林‏. 变分自编码器（二）：从贝叶斯观点出发

苏剑林‏. 变分自编码器（三）：这样做为什么能成？