深入浅出总结求解菲波那切数列的五种方法
文章目录
- 题目
- 思路一: 递归
- 思路二: 递归 + 剪枝 (递归的优化)
- 思路三: 动态规划
- 思路四: 迭代 (动态规划的优化)
- 思路五: 矩阵运算 + 快速幂
题目
菲波那切数列
定义 a0 = 0, a1 = 1, a2 = 1, an = an − 1 + an − 2, 求 an 是多少?
思路一: 递归
由于每一项都遵循这个公式: an = an − 1 + an − 2, 所以就直接递归来实现(普通的递归不需要多讲, 相信你们之前都已经做过了).
代码:
public class Solution {
public int Fibonacci(int n) {
if(n == 0 || n == 1){
return n;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
思路二: 递归 + 剪枝 (递归的优化)
对于上面的普通递归, 会一直在进行深度遍历, 直到 0 或者 1 的时候, 才会返回, 这样的话就会涉及到很多重复计算(非常容易就栈溢出了). 对此我们可以对其进行一下优化: 剪枝.
在这道题中, 我们可以使用哈希表来将每一次计算得到的值存储在哈希表当中, 当下一次需要再计算到这个位置的时候, 就可以直接在哈希表上查找即可, 不需要再继续往下进行深度遍历, 从而达到剪枝的效果.
import java.util.*;
public class Solution {
private Map<Integer, Integer> map = new HashMap<>();
public int Fibonacci(int n) {
if(n == 0 || n == 1){
return n;
}
if(n == 2){
return 1;
}
int ppre = 0;
if(map.containsKey(n - 2)){
ppre = map.get(n - 2);
}else{
ppre = Fibonacci(n - 2);
map.put(n - 2, ppre);
}
int pre = 0;
if(map.containsKey(n - 1)){
pre = map.get(n - 1);
}else{
pre = Fibonacci(n - 1);
map.put(n - 1, pre);
}
return pre + ppre;
}
}
思路三: 动态规划
在这道题中, 我们很简单地就可以找出状态转移方程: q[i] = q[i - 1] + q[i - 2]. 所以直接写即可.
public class Solution {
public int Fibonacci(int n) {
int[] q = new int[n + 1];
q[0] = 0;
q[1] = 1;
for(int i = 2; i <= n; i++){
q[i] = q[i - 1] + q[i - 2];
}
return q[n];
}
}
思路四: 迭代 (动态规划的优化)
由于上面动态规划的做法是需要开辟一个额外的数组来存储每一个位置上的值, 其实我们可以对其进行一下优化, 那就是不要开辟空间来存储这些值, 直接让这些值来内部自己反复迭代计算, 直到最后的那个值就是目标值.
public class Solution {
public int Fibonacci(int n) {
if(n == 0){
return 0;
}
int first = 1;
int second = 1;
int third = 1;
while(n-- > 2){
third = first + second;
first = second;
second = third;
}
return third;
}
}
思路五: 矩阵运算 + 快速幂
这种思路是非常巧妙的, 可以将时间复杂度降到 O(logn).
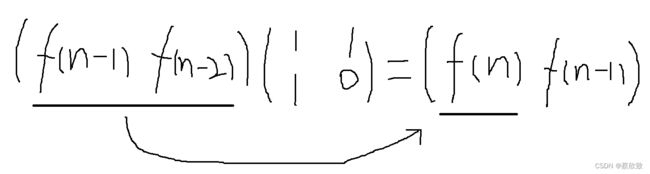
通过这个矩阵运算, 我们就可以将f(n - 1) 和 f(n - 2) 转化成 f(n) 和 f(n - 1). 我们就可以得出一个结论: 每次我们乘上这样的一个矩阵之后, 这些元素就会向后走一步, 那么我们要求第n步之后的结果, 由于我们已经知道了第一步, 那么就只需要区这个矩阵的n - 1次方即可. 因为这里设计到了幂运算, 所以我们就可以很自然地就想到使用快速幂的方法(这种做法推荐有一定算法基础的看看, 了解即可).
public class Solution {
public int Fibonacci(int n) {
if(n == 0 || n == 1){
return n;
}
//矩阵快速幂运算
long[][] t = {{1, 1},{1, 0}};
long[][] res = {{1, 0},{0, 0}};
int count = n - 1;
while(count > 0) {
if((count & 1) == 1) res = mul(res, t); // 注意矩阵乘法顺序,不满足交换律
t = mul(t, t);
count >>= 1;
}
return (int)(res[0][0]);
}
//两矩阵相乘运算
public long[][] mul(long[][] a, long[][] b) {
// 矩阵乘法,新矩阵的行数 = a的行数rowa,列数 = b的列数colb
// a矩阵的列数 = b矩阵的行数 = common
int row = a.length, col = b[0].length, common = b.length;
long[][] res = new long[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
for (int k = 0; k < common; k++) {
res[i][j] += a[i][k] * b[k][j];
}
}
}
return res;
}
}
对于初学者来说, 矩阵快速幂还是有一定难度的, 到后面慢慢学过了之后就不是很难的, 之后代码熟练了之后, 这个矩阵快速幂算法的模板也是要背下来的.