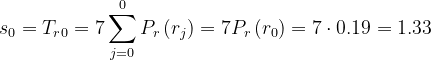OpenCV图像处理学习二十，图像直方图均衡化原理与实现

一.图像直方图的概念

图像直方图，是指对整个图像在灰度范围内的像素值(0~255)统计出现频率次数，据此生成的直方图，称为图像直方图。直方图反映了图像灰度的分布情况,是图像的统计学特征。图像的灰度直方图就描述了图像中灰度分布情况， 能够很直观的展示出图像中各个灰度级所占的多少。图像的灰度直方图是灰度级的函数， 描述的是图像中具有该灰度级的像素的个数： 其中， 横坐标是灰度级， 纵坐标是该灰度级出现的率。

图像直方图表示图像中每一等级像素的个数，反映了图像中每种像素值出现的频率，是图像的基本统计特征之一，具有平移，旋转，缩放不变性，广泛应用于图像处理的各个领域。比如灰度图像的阈值分割，基于颜色的图像检索，图像的分类等。直方图横坐标表示像素值，纵坐标表示该像素值的个数，常见的有灰度直方图和颜色直方图。

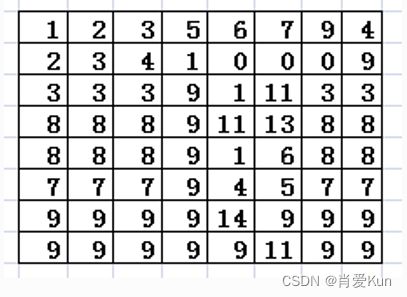
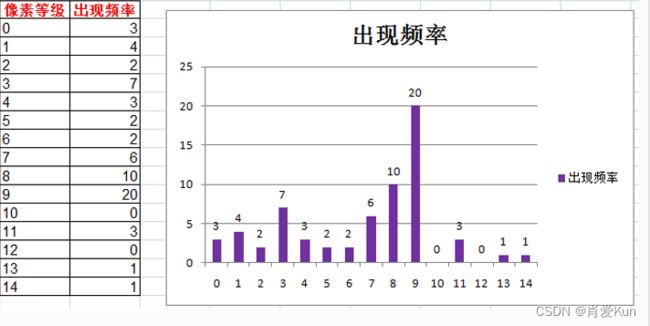
 假设有图像像素分布数据长度和宽度为8x8，像素值范围分为0~14共15个灰度等级，统计得到各个等级出现的像素值次数及直方图如下图所示，每个紫色的长条叫BIN。

直方图中的 BINS, DIMS 和 RANGE

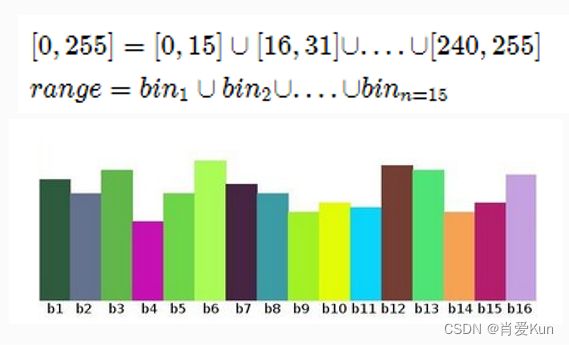
（1）BINS：上面的直方图显示输入图像中的每个像素值的像素数量，即从0到14。即需要14个值来显示上述的直方图（输入图像的像素等级为0-14）。但是并不是所有的图像的像素等级都为0-14，例如，大部分的灰度图像的像素等级为0-255，即一共有256个像素等级，如果需要找到位于0到15之间，然后是16到31，... ，240到255之间的像素值。你只需要16个值来表示直方图（即16×16=256）。这就是OpenCV中的BINS，只是将整个直方图拆分成16个子部分，每个子部分的值是其中所有像素数的总和。这个子部分被称为“BIN”，在OpenCV中，BINS由术语hitSize表示。

（2）DIMS: 表示维度，对灰度图像来说只有一个通道值dims=1

（3）RANGE：这是你要测量的强度值的范围。通常，它是[0,256],即所有强度值。

---------------------------------------------------------------------------------------------------------------------------------

二.直方图均衡化

过曝光图像的灰度级集中在高亮度范围内，而曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。

直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。

实际的直方图均衡化很少能够得到完全平坦的直方图。在离散情况下，通常不能证明离散的直方图均衡化能得到均匀的直方图。尽管如此，均衡化有助于图像直方图的延展，均衡化后图像的灰度级范围更宽，有效地增强了图像的对比度。

-------------------------------------------------------------------------------------------------------------------------------- 

输入图像的像素等级为0-255等级的情况如下,图像的像素总和为255，如下图所示。

将图像像素分为16个像素区间，每个区间包含16个像素，计算每组像素区间的像素数量，如下图所示。

-------------------------------------------------------------------------------------------------------------------------------

三.直方图均衡化的原理

接下来从数学的角度理解直方图均衡化的原理，假设待处理图像为灰度图像，r 表示待处理图像的灰度，取值范围为，则  表示黑色， 表示白色，直方图均衡化的过程对应于一个变换           

                                                                                                            
也就是说，对于输入图像的某个灰度值，可以通过变换公式得到图像均衡化后的图像对应位置的灰度值。其中变换满足以下条件：

(a)    在上严格单调递增；
(b)    当时，也要满足。

条件(a)中严格单调递增是为了保证输出灰度值与输入灰度值一一对应，同时像素灰度值之间的相对大小关系不变，这样可以避免反变换时出现问题；条件(b)保证了输出图像的灰度范围与输入图像相同。实际中处理的图像通常是整数灰度值，必须把所有结果四舍五入为最接近的整数值。因此，当严格单调条件不满足时，使用寻找最接近整数匹配的方法解决反变换不唯一的问题。
 

图像均衡化推导

一幅灰度图像的灰度级可以看作区间内的随机变量，因此可用其概率密度函数(PDF)描述。假设和分别表示随机变量  和  的PDF,和已知 , 且在定义域内连续可微,则变换后  的PDF可由下式得到：
​                                                                                                                  (2)

此处用到了概率论中有关随机变量函数分布的相关定理：设是连续型随机变量，其概率密度函数为，又函数严格单调，其反函数 有连续导数，则也是一个连续型随机变量，其概率密度函数为:

                                              

其中                                       

                                              

由此看到，输出图像灰度 的PDF就由输入图像灰度 的PDF和变换  得到，图像处理中一个重要的变换函数构造如下：

                                                                                       (3)
其中，是形式积分变量，公式右边是随机变量r rr的累积分布函数(CDF)，可以看到，(3)式完全满足前述的条件(a)和(b)，为寻找变换后随机变量 s 的概率密度函数 ,由(2)式得
                                                 (4)

将(4)式代入(2)式得:

                                         (5) 

由(5)式可知，为均匀分布，也就是说，输入图像的PDF经过(3)式中的变换  后得到的随机变量 s 服从均匀分布。
结论：图像均衡化变换  取决于,但得到的 始终是均匀的，与  的形式无关。对于离散形式，其推导过程与连续形式相似，用概率直方图和求和运算分别代替概率密度函数和积分运算，可得(3)式的离散形式:

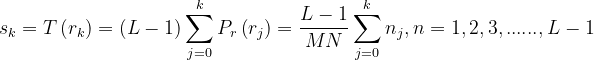                                           (6)
假设一幅大小为 64 × 64  像素的3比特图像的灰度分布如下图所示，其中灰度级是范围 中的整数。
 

	790	0.19
	1023	0.25
	850	0.21
	656	0.16
	329	0.08
	245	0.06
	122	0.03
	81	0.02

则直方图均衡化的值可由 (6) 式计算得到:

                           

同理：   

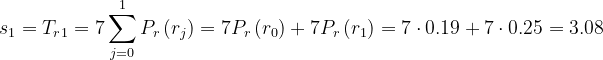                    以此类推计算求得所有 值并将其近似为最接近的整数，结果如下:

                                                 ,

                                                 ,

                                                 ,

                                                 ,

​均衡化后的图像只有5个灰度级， 被映射为 ，在均衡化后的图像中有790个像素取该值，有1023个像素取 ，有850个像素取 ，因为和都被映射为有656+329=985个像素取6，同理，有245+122+81=448个像素取7。

因为直方图是PDF的近似，并且处理后不产生新的灰度级，所以在实际的直方图均衡化很少能够得到完全平坦的直方图。在离散情况下，通常不能证明离散的直方图均衡化能得到均匀的直方图。尽管如此，均衡化有助于图像直方图的延展，均衡化后图像的灰度级范围更宽，有效地增强了图像的对比度。同时，上述方法完全是“自动”的，仅利用输入图像的直方图信息，无需更多的参数。

直方图均衡化原理参考：直方图均衡化_schwein_van的博客-CSDN博客_直方图均衡化

---------------------------------------------------------------------------------------------------------------------------------

四.直方图均衡化API函数接口

void calcHist( 
              const Mat* images, int nimages,
              const int* channels, InputArray mask,
              OutputArray hist, int dims, const int* histSize,
              const float** ranges, bool uniform = true, bool accumulate = false
              );

该函数能够同时计算多个输入图像，多个通道，不同灰度范围的灰度直方图.
其参数如下：

• images，输入图像的数组，这些图像要求大小相同，深度相同（CV_8U CV_16U CV_32F）
• nimages ，输入图像的个数
• channels，要计算直方图的通道个数
• mask，可选的掩码，不使用时可设为空。要和输入图像具有相同的大小，在进行直方图计算的时候，只会统计该掩码不为0的对应像素
• hist，输出的直方图
• dims，直方图的维度
• histSize，直方图每个维度的大小
• ranges，直方图每个维度要统计的灰度级的范围
• uniform，是否进行归一化，默认为true
• accumulate，累积标志，默认值为false。

---------------------------------------------------------------------------------------------------------------------------------

代码实现

#include"stdafx.h"
#include
#include
#include
#include
#include
using namespace std;
using namespace cv;

//绘制直方图，src为输入的图像，histImage为输出的直方图，name是输出直方图的窗口名称
void drawHistImg(Mat &src, Mat &histImage, string name)
{
	const int bins = 256;
	int hist_size[] = { bins };
	float range[] = { 0, 256 };
	const float* ranges[] = { range };
	MatND hist;
	int channels[] = { 0 };

	calcHist(&src, 1, channels, Mat(), hist, 1, hist_size, ranges, true, false);

	double maxValue;
	minMaxLoc(hist, 0, &maxValue, 0, 0);
	int scale = 1;
	int histHeight = 256;

	for (int i = 0; i < bins; i++)
	{
		float binValue = hist.at(i);
		int height = cvRound(binValue*histHeight / maxValue);
		rectangle(histImage, Point(i*scale, histHeight), Point((i + 1)*scale, histHeight - height), Scalar(255));

		imshow(name, histImage);
	}
}

int main(void)
{
	Mat src, dst, image;
    src = imread("F:/photo/lp.jpg");
	if (!src.data)
		cout << "ERR";
	cvtColor(src, image, COLOR_RGB2GRAY);
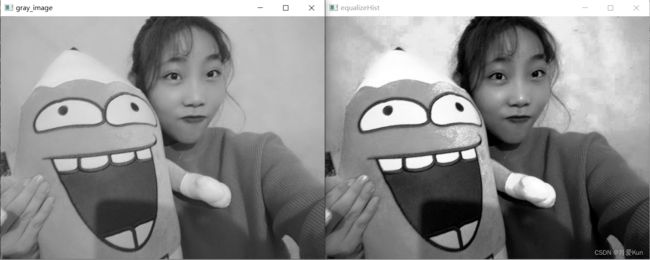
	equalizeHist(image, dst);

	imshow("src", src);
	imshow("equalizeHist", dst);

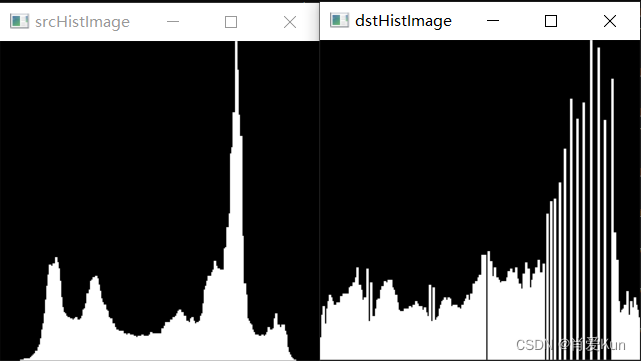
	Mat srcHistImage = Mat::zeros(256, 256, CV_32F);
	Mat dstHistImage = Mat::zeros(256, 256, CV_32F);
	drawHistImg(src, srcHistImage, "srcHistImage");
	drawHistImg(dst, dstHistImage, "dstHistImage");

	waitKey(0);
	return 0;


}

---------------------------------------------------------------------------------------------------------------------------------

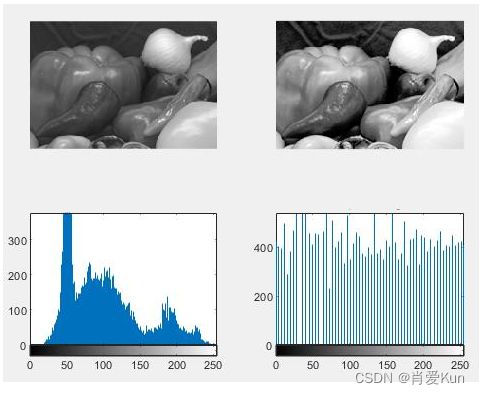
图像处理效果

灰度图和灰度直方图处理

 灰度图直方图和直方图变换效果，对灰度图进行处理后，改变了图像的灰度分布，增强动态范围偏小的图像的对比度。均衡化后图像的灰度级范围更宽，有效地增强了图像的对比度。