Unity/C# 舍入的五种写法
舍入的五种写法
0. 简介
舍入是一个数学概念,一种修约规则。
在日常的生活中,我们为了精简格式,记忆方便,常常会使用四舍五入的方法来去掉零头或凑个整数来解决此类问题。
在游戏中开发中,舍入也是数值计算中重要的一环。只有使用正确的舍入规则,才能配合数值策划进行更合理的数值设计与计算,让玩家在尽量无感的情况下也能认同游戏数值的合理性。
然而在使用Unity进行开发时,我们却发现Unity中Range的结果与日常使用的四舍五入结果并不相同。
这是因为除了四舍五入的舍入方法外还有其他不同的舍入规则、在数学中也有其独特的定义。
本文将从Unity引擎使用的C#语言入手,讲解舍入的5种写法。
0.1 舍入定义
在对位数较多的数进行计算时,为了方便或由于受到计算工具的限制,需要用位数较少的数来代替(有时按照精确度的要求也不必对全部数字进行计算)。
于是,就要按一定的规则去掉一个数的某个有效数字以后的数字,并对剩余部分进行调整,使得尽可能接近于原来那个数。这种过程称为舍入。
0.2 舍入误差定义
舍入误差是指运算得到的近似值和精确值之间的差异。
比如当用有限位数的浮点数来表示实数的时候(理论上存在无限位数的浮点数)就会产生舍入误差。
舍入误差是量化误差的一种形式。
如果在一系列运算中的一步或者几步产生了舍入误差,在某些情况下,误差会随着运算次数增加而积累得很大,最终得出没有意义的运算结果。
舍入误差举例:
增加数字位数可以减少可能会产生的舍入误差,但是位数是有限的,在表示无限浮点数时仍然会产生误差。
在用常规方法表示浮点数的情况下,这种误差是不可避免的,但是可以通过设置警戒位来减小。
多步舍入会增加舍入误差,例如数字9.945309在输入时被舍入到小数点后两位 (9.95),显示时再舍入到小数点后一位(10.0),舍入误差是0.054691。如果原来的数只经过一步舍入到小数点后一位(9.9),舍入误差仅为0.045309。
1 就近舍入
舍入到最接近的,指定精度的原始数字。
对于正数:
-
如果下一位数字从 0 到 4,则最接近的数字为负无穷大。
-
如果下一位数字从 6 到 9,则最接近的数字是正无穷大。
对于负数:
-
如果下一个数字从 0 到 4,则最接近的数字为正无穷大。
-
如果下一位数字从 6 到 9,则最接近的数字为负无穷大。
那么真正有争议的数字就只有5了,所以就近舍入的两种舍入规则,就是针对对数字为5时制定的舍入规则。
1.1 远零舍入 Away From Zero
1.1.1 舍入规则
规则:当数字在两个数字之间的中间时,它将舍入到离零的最接近的数字。
远零舍入就是我们所熟悉的“四舍五入”
1.2 近偶舍入 To Even
1.2.1 舍入规则
规则:当数字在两个数字之间的中间时,它将舍入到最接近的偶数。
近偶舍入也叫做"银行家舍入",或者叫"四舍六入五留双"。
提到四舍五入,处在我们这个年龄层的人应该都很清楚,因为我们当时的小学教育灌输的就是四舍五入。但是如果提到银行家舍入,也许很多朋友会一下子愣住。银行家舍入,英文名为Banker’s round,它实现的舍入效果是“四舍六入五取偶”。
银行家舍入是IEEE规定的小数舍入标准之一,也是IEEE目前规定中最优秀的舍入方法,因此所有符合 IEEE 标准的语言都应该实现这种算法,.NET平台与Unity也不例外。
1.2.2 近偶舍入和远零舍入比较
首先我们比较它们的规则:
-
四舍五入
- 当舍去位的数值大于等于5时,在舍去该位的同时向前位进一
- 当舍去位的数值小于5时,则直接舍去该位
-
近偶舍入
-
所谓银行家舍入法,其实质是一种四舍六入五取偶(又称四舍六入五留双)法。
-
其规则是:
- 当舍去位的数值小于5时,直接舍去该位;
- 当舍去位的数值大于等于6时,在舍去该位的同时向前位进一
- 当舍去位的数值等于5时
- 如果前位数值为奇,则在舍去该位的同时向前位进一
- 如果前位数值为偶,则直接舍去该位。
例如:我们对2.335,2.345,2.364,2.366,2.367分别进行四舍五入和银行家舍入
| 原始数据 | 四舍五入 | 近偶舍入 |
|---|---|---|
| 2.335 | 2.34 | 2.34 |
| 2.345 | 2.35 | 2.34 |
| 2.364 | 2.36 | 2.36 |
| 2.366 | 2.37 | 2.37 |
| 2.367 | 2.37 | 2.37 |
怎么比较它们孰优孰劣呢?
对于1,2,3,4,5,6,7,8,9一系列数,它们出现的随机可能性几乎一样的。
所以如果用四舍五入进行舍取,那么5左右两面奇偶的平衡性就不好,5到9都进位,而1到4都舍去。
如果利用银行家算法,1到4都舍去,6到9都进位,各自四位,然后把5分成两种情况,前位如果是奇数就取偶,如果是偶数就保留,我们发现5前面和5后面奇偶数的个数刚好一样。
当数值精度越大,舍5个概率就越低,无限趋近于0,也就是说,当数值精度越高,该算法越像“四舍五入”
现实情况就是数值的精度不可能无限大,存款利息率一般为百分之零点几,而数值精度一般4位,5后存在非0数的概率相对较小,所以趋近于1/2舍5,1/2进5
所以与四舍五入比较,此时的银行家舍入的公平性更强。
资本家小案例:
我们知道银行的盈利渠道主要是利息差,从储户手里收拢资金,然后放贷出去,其间的利息差额便是所获得的利润。对一个银行来说,对付给储户的利息的计算非常频繁。
场景介绍完毕,我们回过头来看四舍五入,小于5的数字被舍去,大于等于5的数字进位加一,由于所有位上的数字都是自然计算出来的,按照概率计算可知,被舍入的数字均匀分布在0到9之间,下面以10笔存款利息计算作为模型,以银行家的身份来思考这个算法:
(1)四舍:舍弃的数值:0.000、0.001、0.002、0.003、0.004,因为是舍弃,对银行家来说,就是不用付款给储户的,那每舍弃一个数字就会赚取相应的金额:0.000、0.001、0.002、0.003、0.004。
(2)五入:进位的数值:0.005、0.006、0.007、0.008、0.009,因为是进位,对银行家来说,每进一位就会多付款给储户,也就是亏损了,那亏损部分就是其对应的10进制补数:0.005、0.004、0.003、0.002、0.001
因为舍弃和进位的数字是在0到9之间均匀分布的,所以对于银行家来说,每10笔存款的利息因采用四舍五入而获得的盈利是:
0.000 + 0.001 + 0.002 + 0.003 + 0.004 - 0.005 - 0.004 - 0.003 - 0.002 - 0.001 = -0.005
也就是说,每10笔的利息计算中就亏损0.005元,即每笔利息计算损失0.0005元
这个算法误差是由美国银行家发现的,并且对此提出了一个修正算法,就叫作银行家舍入
“银行家舍入”是IEEE754标准的推荐舍入标准。
因此所有符合 IEEE标准 的语言都是采用这一算法的,Unity与C#也不例外。
这一方式跟通常的四舍五入相比,平均数方面更能保持原有数据的特性。
2 定向舍入
定向舍入则不在乎精确位的下一位的数字是什么,它直接规定向某个方向进行舍入。
也就是说定向舍入的区别主要就是在舍入方向上。
数轴上有三个方向分别是:
-
+∞ 正无穷
-
0 零
-
-∞ 负无穷
因此定向舍入也有三种规则,分别对应这三个方向。
2.1 向上舍入 To Positive Infinity
规则:向上定向舍入,结果最接近且不小于无限精确结果
2.2 向下舍入 To Negative Infinity
规则:向下定向舍入,结果最接近且不大于无限精确结果。
2.3 向零舍入 To Zero
规则:向零舍入的策略,结果最接近且数量级不大于无限精确结果。
3. 整理总结表
| 舍入方法 | 舍入规则 | 舍入特点 | 适用场景 | 精确度 | 舍入案例 |
|---|---|---|---|---|---|
| 远零舍入 Away From Zero |
当数字在两个数字之间的中间时 它将舍入到离零的最接近的数字 |
国内约定俗成的四舍五入方法 | 需要迎合国内用户理解的舍入场景 (玩家可感的数据取舍) |
一般 | 2.4≈2 2.5≈3 -2.4≈-2 -2.5≈-3 |
| 近偶舍入 To Even |
当数字在两个数字之间的中间时它将舍入到最接近的偶数 | 外国,Unity使用的舍入方法 大量数据下比远零舍入分布的更加均匀,更科学 |
各种需要精确取舍的数据均可使用 (各种游戏数值公式计算) |
高 | 2.4≈2 2.5≈2 -2.4≈-2 -2.5≈-2 3.4≈3 3.5≈4 -3.4≈-3 -3.5≈-4 |
| 向上舍入 To Positive Infinity |
向上定向舍入 | 往往大于精确结果 | 需要取舍且只能往大估的情景 | 低 | 2.4≈3 2.5≈3 -2.4≈-2 -2.5≈-2 |
| 向下舍入 To Negative Infinity |
向下定向舍入 | 往往小于精确结果 | 需要取舍且只能往小估的情景 | 低 | 2.4≈2 2.5≈2 -2.4≈-3 -2.5≈-3 |
| 向零舍入 To Zero |
向零舍入的策略 | 往往数量级不会大于精确结果 | 只在乎精确位数之前数据的情景 | 低 | 2.4≈2 2.5≈2 -2.4≈-2 -2.5≈-2 |
4. 在Unity/C#中使用这五种舍入
在使用Unity与C#进行游戏开发的过程中,一般会使用Round这个类进行舍入操作。而这个类实际上是来自不同命名空间的两个类:
一个来自C# 的 System.Math.Round,另一个则来自Unity引擎的UnityEngine.Mathf.Round。
4.1 UnityEngine.Mathf.Round
可以看到Unity的Mathf中只是把C#的代码封装了一层,本质上还是C# 的 Math。
而且Mathf.Round只能取整,并不能按精度取舍。
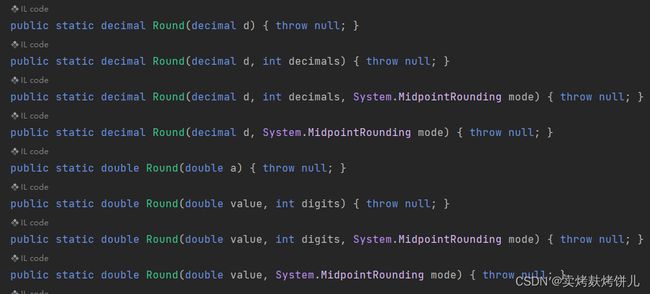
4.2 System.Math.Round
可以看出C#的Round就有更多的可操作空间了,其中的参数:MidpointRounding,就是我们前面说到的五种舍入规则的枚举。
而不传这个参数的方法将默认使用近偶舍入的舍入规则。
也就是说使用Unity Mathf.Round进行取整会默认使用近偶舍入规则。
这也就解释了最开始我们的疑问,为什么有时使用Unity进行取整会和四舍五入的结果不同。
MidpointRounding枚举的官方文档说明如下:
代码案例:
decimal result;
// 正数情况
result = Math.Round(3.45m, 1, MidpointRounding.ToEven);
Console.WriteLine($"{result} = Math.Round({3.45m}, 1, MidpointRounding.ToEven)");
result = Math.Round(3.45m, 1, MidpointRounding.AwayFromZero);
Console.WriteLine($"{result} = Math.Round({3.45m}, 1, MidpointRounding.AwayFromZero)");
result = Math.Round(3.47m, 1, MidpointRounding.ToZero);
Console.WriteLine($"{result} = Math.Round({3.47m}, 1, MidpointRounding.ToZero)\n");
// 负数情况
result = Math.Round(-3.45m, 1, MidpointRounding.ToEven);
Console.WriteLine($"{result} = Math.Round({-3.45m}, 1, MidpointRounding.ToEven)");
result = Math.Round(-3.45m, 1, MidpointRounding.AwayFromZero);
Console.WriteLine($"{result} = Math.Round({-3.45m}, 1, MidpointRounding.AwayFromZero)");
result = Math.Round(-3.47m, 1, MidpointRounding.ToZero);
Console.WriteLine($"{result} = Math.Round({-3.47m}, 1, MidpointRounding.ToZero)\n");
/*
结果输出:
3.4 = Math.Round(3.45, 1, MidpointRounding.ToEven)
3.5 = Math.Round(3.45, 1, MidpointRounding.AwayFromZero)
3.4 = Math.Round(3.47, 1, MidpointRounding.ToZero)
-3.4 = Math.Round(-3.45, 1, MidpointRounding.ToEven)
-3.5 = Math.Round(-3.45, 1, MidpointRounding.AwayFromZero)
-3.4 = Math.Round(-3.47, 1, MidpointRounding.ToZero)
*/
5. 参考文献
MidpointRounding 枚举 (System) | Microsoft Docs
Math.Round 方法 (System) | Microsoft Docs
舍入_百度百科 (baidu.com)
B站同步讲解视频:
https://www.bilibili.com/video/BV1tV4y1p7aZ/