深度学习经典网络解析图像分类篇（二）：AlexNet

1.背景介绍

  在上篇深度学习经典网络解析（一）：LeNet-5中我们提到，LeNet-5创造了卷积神经网络，但是LeNet-5并没有把CNN发扬光大，是CNN真正开始走进人们视野的是今天要介绍的——AlexNet网络。AlexNet网络源自于《ImageNet Classification with Deep Convolutional Neural Networks》这篇论文。作者是是Hinton率领的谷歌团队（Alex Krizhevsky，Ilya Sutskever，Geoffrey E. Hinton），Hinton在上一篇博客我们也曾介绍过，他是深度学习之父，在人工智能寒冬时期，Hinton一直就默默地坚持深度网络的方向，终于在2006年的《Science》上提出了DNN，为如今深度学习的繁荣奠定了基础。AlexNet利用了两块GPU进行计算，大大提高了运算效率，并且在ILSVRC-2012竞赛中获得了top-5测试的15.3%error rate， 获得第二名的方法error rate 是 26.2%，可以说差距是非常的大了，足以说明这个网络在当时给学术界和工业界带来的冲击之大。

  之所以叫AlexNet网络是因为这篇文章过于经典，后人们常常哪来在论文中比较，将论文的一作（Alex Krizhevsky）与Net结合，故称做AlexNet。AlexNet是在2010年ImageNet大赛获得冠军的一个神经网络，它引入图像增强，Dropout等技术，同时把网络分布在两个GPU进行计算，大大提高了运算效率，并且在ILSVRC-2012竞赛中获得了top-5测试的15.3%error rate， 获得第二名的方法error rate 是 26.2%，比第二名高了近10个点。

2.ImageNet

  ImageNet项目是一个用于视觉对象识别软件研究的大型可视化数据库。超过1400万的图像URL被ImageNet手动注释，以指示图片中的对象;在至少一百万个图像中，还提供了边界框。ImageNet包含2万多个类别; 一个典型的类别，如“气球”或“草莓”，包含数百个图像。第三方图像URL的注释数据库可以直接从ImageNet免费获得;但是，实际的图像不属于ImageNet。自2010年以来，ImageNet项目每年举办一次软件比赛，即ImageNet大规模视觉识别挑战赛（ILSVRC），软件程序竞相正确分类检测物体和场景。 ImageNet挑战使用了一个“修剪”的1000个非重叠类的列表。2012年在解决ImageNet挑战方面取得了巨大的突破，被广泛认为是2010年的深度学习革命的开始。

3.AlexNet

3.1AlexNet简介

  AlexNet是在LeNet的基础上加深了网络的结构，学习更丰富更高维的图像特征。AlexNet的特点：

1. 提出了一种卷积层加全连接层的卷积神经网络结构。
2. 首次使用ReLU函数做为神经网络的激活函数。
3. 首次提出Dropout正则化来控制过拟合。
4. 使用加入动量的小批量梯度下降算法加速了训练过程的收敛。
5. 使用数据增强策略极大地抑制了训练过程的过拟合。
6. 利用了GPU的并行计算能力，加速了网络的训练与推断。

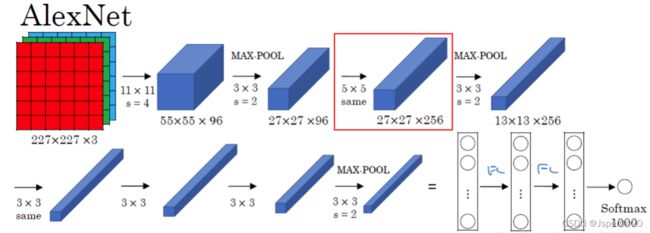
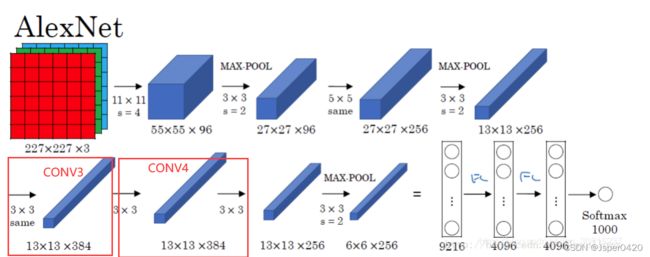
3.2AlexNet网络架构

  AlexNet网络共有：卷积层 5个，池化层 3个，局部响应归一化层：2个，全连接层：3个。
层数统计说明：
  AlexNet共8层: 5个卷积层(CONV1——CONV5) 3个全连接层(FC6-FC8)

• ➢ 计算网络层数时仅统计卷积层与全连接层；
• ➢ 池化层与各种归一化层都是对它们前面卷积层输出的特征图进行后处理，不单独算作一层。

3.2.1第一层（CONV1）

第一层 (CONV1): 96 个11x11 卷积核，步长为 4，没有零填充

• 输入:227x227x3 大小的图像
• 尺寸：(227-11)/4+1 = 55
• 卷积核个数：96
• 参数: (11113+1)*96 = 35K
  第一个卷积层提取了96种结构的响应信息，得到了96个特征相应图； 特征图每个元素经过ReLU函数操作后输出。
  

3.2.2 MAX POOL1+NORM1层

Max POOL1: 窗口大小3x3，步长为 2 （窗口会有重叠，有助于对抗过拟合）

• 作用：降低特征图尺寸，对抗轻微的目标偏移带来的影响
• 输出尺寸： (55-3)/2+1 =27
• 特征图个数：96
• 参数个数：0

局部相应归一化层（NORM1）作用:

• ➢ 对局部神经元的活动创建竞争机制。
• ➢ 响应比较大的值变得相对更大。
• ➢ 抑制其他反馈较小的神经元。
• ➢ 增强模型的泛化能力。

后来的研究表明：
更深的网络中该层对分类性能的提升效果并不明显，且会增加计算量与存储空间。

3.2.3第三层（CONV2）

第三层 (CONV2): 96 个5x5 卷积核，步长为 1，使用零填充p=2

• 输入: 27x27x96 大小的特征图组
• 输出特征图尺寸：(27 - 5 + 2*2)/1+1 = 27
• 卷积核个数：256（增强基元的描述能力）
  

3.2.4 MAX POOL2+NORM2层

Max POOL1: 窗口大小3x3，步长为 2 （窗口会有重叠，有助于对抗过拟合）

• 作用：降低特征图尺寸，对抗轻微的目标偏移带来的影响
• 输出尺寸： (27-3)/2+1 =213
• 特征图个数：256

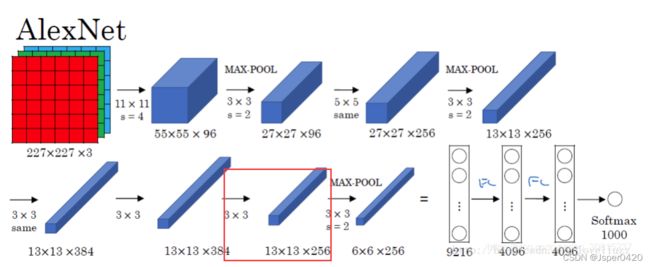
3.2.5第三、四层（CONV3、CONV4）

第三、四层(CONV3、CONV4): 384 个3x3 卷积核，步长为 1，使用零填充p=1

• CONV3输入: 13x13x256 大小的特征图组
• 输出特征图尺寸：(13 - 3 + 2*1)/1+1 = 13
• 输出特征图个数：384
  第三、四层(CONV3、CONV4):之后没有进行最大池化与局部归一化
  

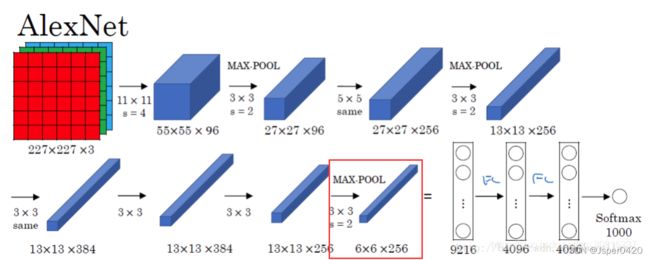
3.2.6第五层（CONV5）

第五层 (CONV5): 256 个3x3 卷积核，步长为 1，使用零填充p=1

• CONV3输入: 13x13x384 大小的特征图组
• 输出特征图尺寸：(13 - 3 + 2*1)/1+1 = 13
• 输出特征图个数：256
  

3.2.7MAX POOL3层

MAX POOL3层用来进一步缩小特征图尺寸
Max POOL3: 窗口大小3x3，步长为 2 （窗口会有重叠，有助于对抗过拟合）

• 作用：降低特征图尺寸，对抗轻微的目标偏移带来的影响
• 输出尺寸： (13-3)/2+1 =6
• 特征图个数：256
  

3.2.8第六七八层—全连接层

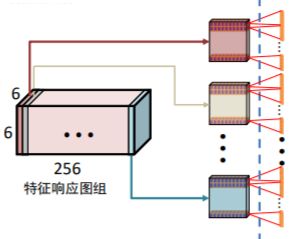
MAX POOL3的输出：特征响应图组

但是FC6期望输入：向量

如何解决？

Flatten层用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。

x = torch.tensor([[1,2], [3,4], [5,6]])
x = x.flatten(0)
print(x)
tensor([1, 2, 3, 4, 5, 6])
----------------------------------------------------------------------------------------------------
x = torch.tensor([[[1,2],[3,4]], [[5,6],[7,8]]])
x = x.flatten(1)
print(x)
tensor([[1, 2],
        [3, 4],
        [5, 6]])

FC6输入：9216维向量
FC6输出：4096维向量

FC7输入：4096维向量
FC7输出：4096维向量

FC8输入：4096维向量
FC8输出：1000维向量（1000个类别）

3.3AlexNet创新点

3.3.1数据增强

随机缩放&抠图：
输入要求：224x224的彩色图片
训练阶段: 在不同尺度、不同区域随机扣取

1. 在[256, 480]之间随机选择一个尺寸L
2. 将训练样本缩放至短边 = L
3. 在该样本上随机采样一个224 x 224的图像区域

测试阶段: 按照一套预先定义的方式扣取

1. 将图像缩放成5种尺寸: {224, 256, 384, 480, 640}
2. 对每一个尺度的图像及其镜像图像，分别在其四个角及中间位 置扣取224 x 224区域，即可获得10个图像

色彩抖动：

操作步骤：

1. 利用主成分分析方法提取当前图像的色彩数
   据（[R G B]）的主轴；
2. 沿着主轴方向随机采样一个偏移；
3. 将偏移量加入当前图像的每个像素。

其他方案：

平移、旋转、拉伸、径向畸变（相关描述见摄像机几何章节）、裁剪

AlexNet中使用了两种增大数据量的方法镜像反射和随机剪裁和改变训练样本RGB通道的强度值

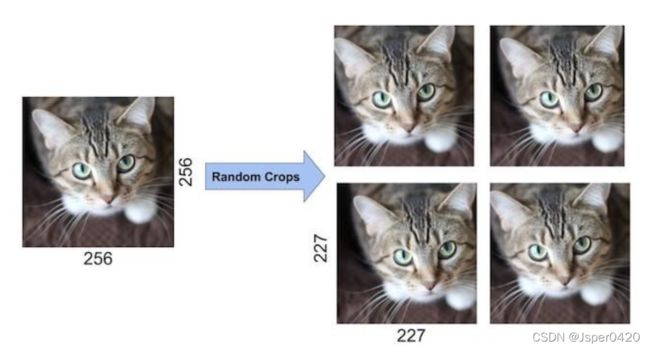
方法一： 镜像反射和随机剪裁

然后在原图和镜像反射的图（256×256）中随机抽取227×227的块，相当与将样本倍*增到原来的 ((256-227)^2)2=2048倍。虽然这样训练样例会产生高度的相互依赖。但是不使用这种方法又会导致严重的过拟合，迫使我们使用更小的网络。在测试的时候，AlexNet会抽取测试样本及其镜像反射图各5块（总共10块，四个角和中心位置）来进行预测，预测结果是这10个块的softmax块的平均值。

方法二： 改变训练样本RGB通道的强度值

  Alex团队在整个训练集中对图片的RGB像素值集执行PCA（主成分分析，Principal Components Analysis）。对于每一张训练图片，他们增加了多个找到的主成分，它们的大小比例是相应的特征值乘以一个随机值（来自均值为0，标准差为0.1的高斯分布）， 对于每张训练图片，我们通过均值为0方差为 $0.1$ 的高斯分布产生一个随机值a，然后通过向图像中加入更大比例相应特征值的a倍，把其主 成分翻倍。因此，对于每个RGB图像像素 Ixy= [ IxyR,Ixy,G IxyB]T，我们增加下面这项:
$$\left[{\mathrm{p}}_1,{\mathrm{p}}_2,{\mathrm{p}}_3\right]{\left[{\alpha }_1{\lambda }_1,{\alpha }_2{\lambda }_2,{\alpha }_3{\lambda }_3\right]}^T$$
  其中Pi与 i分别是RGB像素 $3\times 3$ 协方差矩阵的第 $\mathrm{i}$ 个特征向量与特征值， ai 是前面提到的随机变量。对于特定训练图像的所有像素每个ai 仅 提取一次，直到这张图再次被用于训练才会再次提取随机变量。这个方案大致抓住了原始图片的重要特征，即那些不随光线强度与颜色变化的物体特征。该方法将top-1误差率降低1%以上。

3.3.2 Dropout随机失活

  Dropout是通过遍历神经网络每一层的节点，然后通过对该层的神经网络设置一个keep_prob(节点保留概率)，即该层的节点有keep_prob的概率被保留，keep_prob的取值范围在0到1之间。每个隐层神经元有keep_prob的概率的输出设置为零。以这种方式“dropped out”的神经元既不参与前向传播，也不参与反向传播。

  通过Dropout每次输入一个样本，就相当于该神经网络就尝试了一个新的结构，但是所有这些结构之间共享权重。因为神经元不能依赖于其他特定神经元而存在，所以这种技术降低了神经元复杂的互适应关系。正因如此，网络需要被迫学习更为鲁棒的特征（泛化性更强）。

3.3.3 非线性ReLU函数

  Sigmoid 是常用的非线性的激活函数，它能够把输入的连续实值“压缩”到0和1之间。特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

  但是它有一些致命的缺点：

  当输入非常大或者非常小的时候，会有饱和现象，这些神经元的梯度是接近于0的。如果你的初始值很大的话，梯度在反向传播的时候因为需要乘上一个sigmoid 的导数，所以会使得梯度越来越小，最终导致梯度消失。Alex用ReLU代替了Sigmoid，发现使用 ReLU 得到的SGD的收敛速度会比 Sigmoid/Tanh 快很多。

3.3.4 Local Responce Normalization(NORM层)

  LRN是一种提高深度学习准确度的技术方法。LRN一般是在激活、池化函数后的一种方法。 在ALexNet中，提出了LRN层，对局部神经元的活动创建竞争机制，使其中响应比较大对值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。
  总结的来说，是对输入值 $a_{x,y}^2$ 除以一个数达到归一化的目的。$b_{x,y}^i$是归一化后的值，i是通道的位置，代表更新第几个通道的值，x与y代表待更新像素的位置。具体计算公式如下:
$$b_{x,y}^i=a_{x,y}^i/{\left(k+\alpha \sum _{j=\max (0,i-n/2)}^{\min (N-1,i+n/2)}{\left(a_{x,y}^j\right)}^2\right)}^{\beta }$$

4.用PyTorch实现AlexNet

import torch.nn as nn


class AlexNet(nn.Module):
    def __init__(self, num_classes=1000):
        super(AlexNet, self).__init__()
        self.features = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(64, 192, kernel_size=5, padding=2),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
            nn.Conv2d(192, 384, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(384, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.Conv2d(256, 256, kernel_size=3, padding=1),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2),
        )
        self.classifier = nn.Sequential(
            nn.Linear(256 * 6 * 6, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, 4096),
            nn.ReLU(inplace=True),
            nn.Linear(4096, num_classes),
        )

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size(0), 256 * 6 * 6)
        x = self.classifier(x)
        return x


if __name__ == '__main__':
    # Example
    net = AlexNet()
    print(net)

Output:
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 96, 55, 55]          34,944
              ReLU-2           [-1, 96, 55, 55]               0
         MaxPool2d-3           [-1, 96, 27, 27]               0
            Conv2d-4          [-1, 256, 27, 27]         614,656
              ReLU-5          [-1, 256, 27, 27]               0
         MaxPool2d-6          [-1, 256, 13, 13]               0
            Conv2d-7          [-1, 384, 13, 13]         885,120
              ReLU-8          [-1, 384, 13, 13]               0
            Conv2d-9          [-1, 384, 13, 13]       1,327,488
             ReLU-10          [-1, 384, 13, 13]               0
           Conv2d-11          [-1, 256, 13, 13]         884,992
             ReLU-12          [-1, 256, 13, 13]               0
        MaxPool2d-13            [-1, 256, 6, 6]               0
AdaptiveAvgPool2d-14            [-1, 256, 6, 6]               0
          Dropout-15                 [-1, 9216]               0
           Linear-16                 [-1, 4096]      37,752,832
             ReLU-17                 [-1, 4096]               0
          Dropout-18                 [-1, 4096]               0
           Linear-19                 [-1, 4096]      16,781,312
             ReLU-20                 [-1, 4096]               0
           Linear-21                 [-1, 1000]       4,097,000
================================================================
Total params: 62,378,344
Trainable params: 62,378,344
Non-trainable params: 0
----------------------------------------------------------------