leetcode 队列 栈
队列/栈
文章目录
- 队列/栈
- [232. 用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)
-
- 思路分析
- 代码实现
- [225. 用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)
-
- 思路分析
- 代码实现
- [20. 有效的括号](https://leetcode-cn.com/problems/valid-parentheses/)
-
- 思路分析
- 代码实现
- [921. 使括号有效的最少添加](https://leetcode-cn.com/problems/minimum-add-to-make-parentheses-valid/)
-
- 思路分析
- 代码实现
- [1541. 平衡括号字符串的最少插入次数](https://leetcode-cn.com/problems/minimum-insertions-to-balance-a-parentheses-string/)
-
- 思路分析
- 代码实现
- [496. 下一个更大元素 I](https://leetcode-cn.com/problems/next-greater-element-i/)
-
- 思路分析
- 代码实现
- [503. 下一个更大元素 II](https://leetcode-cn.com/problems/next-greater-element-ii/)
-
- 思路分析
- 代码实现
- [239. 滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)
-
- 思路分析
- 代码实现
- [316. 去除重复字母](https://leetcode-cn.com/problems/remove-duplicate-letters/)
-
- 思路分析
- 代码实现
- [380. O(1) 时间插入、删除和获取随机元素](https://leetcode-cn.com/problems/insert-delete-getrandom-o1/)
-
- 思路分析
- 代码实现
- [710. 黑名单中的随机数](https://leetcode-cn.com/problems/random-pick-with-blacklist/)
-
- 思路分析
- 代码实现
- [295. 数据流的中位数](https://leetcode-cn.com/problems/find-median-from-data-stream/)
-
- 思路分析
- 代码实现
232. 用栈实现队列
思路分析
我们使用两个栈s1, s2就能实现一个队列的功能(这样放置栈可能更容易理解):
class MyQueue {
private Stack<Integer> s1, s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
// ...
}
当调用push让元素入队时,只要把元素压入s1即可,比如说push进 3 个元素分别是 1,2,3,那么底层结构就是这样:
/** 添加元素到队尾 */
public void push(int x) {
s1.push(x);
}
那么如果这时候使用peek查看队头的元素怎么办呢?按道理队头元素应该是 1,但是在s1中 1 被压在栈底,现在就要轮到s2起到一个中转的作用了:
当s2为空时,可以把s1的所有元素取出再添加进s2,这时候s2中元素就是先进先出顺序了。
/** 返回队头元素 */
public int peek() {
if (s2.isEmpty())
// 把 s1 元素压入 s2
while (!s1.isEmpty())
s2.push(s1.pop());
return s2.peek();
}
同理,对于pop操作,只要操作s2就可以了。
/** 删除队头的元素并返回 */
public int pop() {
// 先调用 peek 保证 s2 非空
peek();
return s2.pop();
}
最后,如何判断队列是否为空呢?如果两个栈都为空的话,就说明队列为空:
/** 判断队列是否为空 */
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
代码实现
/**
* https://leetcode-cn.com/problems/implement-queue-using-stacks/
*
* @author xiexu
* @create 2022-01-24 6:02 下午
*/
public class _232_用栈实现队列 {
}
class MyQueue {
private Stack<Integer> s1, s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
/**
* 添加元素到队尾
*/
public void push(int x) {
s1.push(x);
}
/**
* 删除队头的元素并返回
*/
public int pop() {
// 先调⽤ peek 保证 s2 ⾮空
peek();
return s2.pop();
}
/**
* 返回队头元素
*/
public int peek() {
if (s2.isEmpty()) {
// 把 s1 元素压入 s2
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
}
return s2.peek();
}
/**
* 判断队列是否为空
*/
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
}
225. 用队列实现栈
思路分析
先说pushAPI,直接将元素加入队列,同时记录队尾元素,因为队尾元素相当于栈顶元素,如果要top查看栈顶元素的话可以直接返回:
class MyStack {
Queue<Integer> q = new LinkedList<>();
int top_elem = 0;
/** 添加元素到栈顶 */
public void push(int x) {
// x 是队列的队尾,是栈的栈顶
q.offer(x);
top_elem = x;
}
/** 返回栈顶元素 */
public int top() {
return top_elem;
}
}
我们的底层数据结构是先进先出的队列,每次pop只能从队头取元素;但是栈是后进先出,也就是说popAPI 要从队尾取元素。
解决方法简单粗暴,把队列前面的都取出来再加入队尾,让之前的队尾元素排到队头,这样就可以取出了:
/** 删除栈顶的元素并返回 */
public int pop() {
int size = q.size();
while (size > 1) {
q.offer(q.poll());
size--;
}
// 之前的队尾元素已经到了队头
return q.poll();
}
这样实现还有一点小问题就是,原来的队尾元素被提到队头并删除了,但是top_elem变量没有更新,我们还需要一点小修改:
/** 删除栈顶的元素并返回 */
public int pop() {
int size = q.size();
// 留下队尾 2 个元素
while (size > 2) {
q.offer(q.poll());
size--;
}
// 记录新的队尾元素
top_elem = q.peek();
q.offer(q.poll());
// 删除之前的队尾元素
return q.poll();
}
最后,APIempty就很容易实现了,只要看底层的队列是否为空即可:
/** 判断栈是否为空 */
public boolean empty() {
return q.isEmpty();
}
代码实现
/**
* https://leetcode-cn.com/problems/implement-stack-using-queues/
*
* @author xiexu
* @create 2022-01-24 6:23 下午
*/
public class _225_用队列实现栈 {
}
class MyStack {
Queue<Integer> q = new LinkedList<>();
int top_elem = 0;
public MyStack() {
}
/**
* 添加元素到栈顶
*/
public void push(int x) {
// x 是队列的队尾,是栈的栈顶
q.offer(x);
top_elem = x;
}
/**
* 删除栈顶的元素并返回
*/
public int pop() {
int size = q.size();
// 留下队尾 2 个元素
while (size > 2) {
q.offer(q.poll());
size--;
}
// 记录新的队尾元素
top_elem = q.peek();
q.offer(q.poll());
// 删除之前的队尾元素
return q.poll();
}
/**
* 返回栈顶元素
*/
public int top() {
return top_elem;
}
/**
* 判断栈是否为空
*/
public boolean empty() {
return q.isEmpty();
}
}
20. 有效的括号
思路分析
我们这道题就用一个名为left的栈代替之前思路中的left变量,遇到左括号就入栈,遇到右括号就去栈中寻找最近的左括号,看是否匹配;
代码实现
/**
* https://leetcode-cn.com/problems/valid-parentheses/
*
* @author xiexu
* @create 2022-01-24 6:39 下午
*/
public class _20_有效的括号 {
public boolean isValid(String s) {
Stack<Character> left = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(' || c == '{' || c == '[') {
left.push(c);
} else { // 字符 c 是右括号
if (!left.isEmpty() && leftOf(c) == left.peek()) {
left.pop();
} else {
// 和最近的左括号不匹配
return false;
}
}
}
// 是否所有的左括号都被匹配了
return left.isEmpty();
}
public char leftOf(char c) {
if (c == '}') {
return '{';
}
if (c == ')') {
return '(';
}
return '[';
}
}
921. 使括号有效的最少添加
思路分析
给你输入一个字符串s,你可以在其中的任意位置插入左括号(或者右括号),请问你最少需要几次插入才能使得s变成一个合法的括号串?
比如说输入s = "())(",算法应该返回 2,因为我们至少需要插入两次把s变成"(())()",这样每个左括号都有一个右括号匹配,s是一个合法的括号串。
当
need == -1的时候意味着什么?
- 因为只有遇到右括号
)的时候才会need--,need == -1意味着右括号太多了,所以需要插入左括号。 - 比如说
s = "))"这种情况,需要插入 2 个左括号,使得s变成"()()",才是一个合法括号串。
算法为什么返回
res + need?
- 因为
res记录的左括号的插入次数,need记录了右括号的需求,当 for 循环结束后,若need不为 0,那么就意味着右括号还不够,需要插入。 - 比如说
s = "))("这种情况,插入 2 个左括号之后,还要再插入 1 个右括号,使得s变成"()()()",才是一个合法括号串。
代码实现
/**
* https://leetcode-cn.com/problems/minimum-add-to-make-parentheses-valid/
*
* @author xiexu
* @create 2022-01-24 9:25 下午
*/
public class _921_使括号有效的最少添加 {
public int minAddToMakeValid(String s) {
// res 记录插入次数
int res = 0;
// need 变量记录右括号的需求量
int need = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
// 对右括号的需求 + 1
need++;
}
if (s.charAt(i) == ')') {
// 对右括号的需求 - 1
need--;
if (need == -1) {
need = 0;
// 需插入一个左括号
res++;
}
}
}
return res + need;
}
}
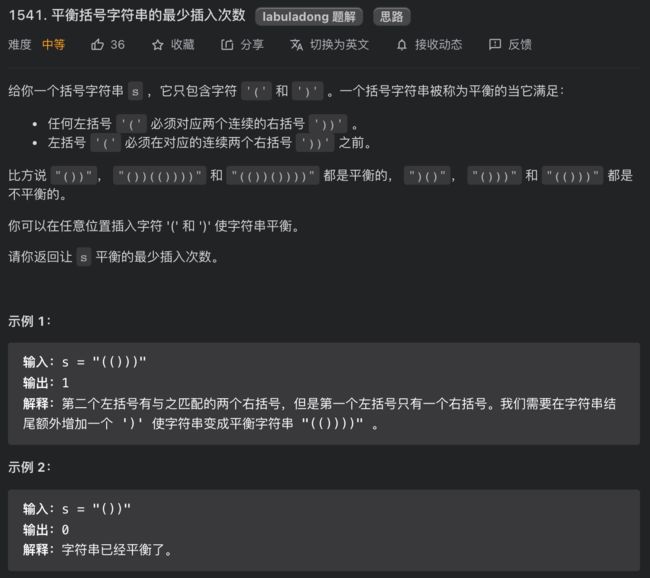
1541. 平衡括号字符串的最少插入次数
思路分析
第一步,我们按照刚才的思路正确维护need变量:
int minInsertions(string s) {
// need 记录需右括号的需求量
int res = 0, need = 0;
for (int i = 0; i < s.size(); i++) {
// 一个左括号对应两个右括号
if (s[i] == '(') {
need += 2;
}
if (s[i] == ')') {
need--;
}
}
return res + need;
}
现在想一想,当need是什么值的时候,我们可以确定需要进行插入?
首先,类似第一题,当need == -1时,意味着我们遇到一个多余的右括号,显然需要插入一个左括号。
比如说当s = ")",我们肯定需要插入一个左括号让s = "()",但是由于一个左括号需要两个右括号,所以对右括号的需求量变为 1:
if (s[i] == ')') {
need--;
// 说明右括号太多了
if (need == -1) {
// 需要插入一个左括号
res++;
// 同时,对右括号的需求变为 1
need = 1;
}
}
另外,当遇到左括号时,若对右括号的需求量为奇数,需要插入 1 个右括号。因为一个左括号需要两个右括号嘛,右括号的需求必须是偶数,这一点也是本题的难点。
所以遇到左括号时要做如下判断:
if (s[i] == '(') {
need += 2;
if (need % 2 == 1) {
// 插入一个右括号
res++;
// 对右括号的需求减一
need--;
}
}
代码实现
/**
* https://leetcode-cn.com/problems/minimum-insertions-to-balance-a-parentheses-string/
*
* @author xiexu
* @create 2022-01-24 9:35 下午
*/
public class _1541_平衡括号字符串的最少插入次数 {
public int minInsertions(String s) {
// res 记录插入次数
int res = 0;
// need 变量记录右括号的需求量
int need = 0;
for (int i = 0; i < s.length(); i++) {
// 一个左括号对应两个右括号
if (s.charAt(i) == '(') {
need += 2;
if (need % 2 == 1) {
// 插入一个右括号
res++;
// 对右括号的需求减一
need--;
}
}
if (s.charAt(i) == ')') {
// 对右括号的需求 - 1
need--;
// 说明右括号太多了
if (need == -1) {
// 需要插入一个左括号
res++;
// 同时,对右括号的需求变为 1
need = 1;
}
}
}
return res + need;
}
}
496. 下一个更大元素 I
思路分析
代码实现
/**
* https://leetcode-cn.com/problems/next-greater-element-i/
*
* @author xiexu
* @create 2022-01-24 9:51 下午
*/
public class _496_下一个更大元素_I {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int[] res = new int[nums1.length];
Map<Integer, Integer> map = nextGreaterElement(nums2);
for (int i = 0; i < nums1.length; i++) {
res[i] = map.get(nums1[i]);
}
return res;
}
// 单调栈模板
public Map<Integer, Integer> nextGreaterElement(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
Stack<Integer> stack = new Stack<>(); // 存放高个元素的栈
// 倒着往栈里放
for (int i = nums.length - 1; i >= 0; i--) {
// 判断个子高矮
while (!stack.isEmpty() && stack.peek() <= nums[i]) {
// 矮个起开,反正也被挡着了...
stack.pop();
}
// 当前元素身后的第一个高个
map.put(nums[i], stack.isEmpty() ? -1 : stack.peek());
stack.push(nums[i]); // 进队,接受之后的身高判定
}
return map;
}
}
503. 下一个更大元素 II
思路分析
比如输入一个数组[2,1,2,4,3],你返回数组[4,2,4,-1,4]。拥有了环形属性,最后一个元素 3 绕了一圈后找到了比自己大的元素 4。
一般是通过 % 运算符求模(余数),来获得环形特效:
int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
print(arr[index % n]);
index++;
}
这个问题肯定还是要用单调栈的解题模板,但难点在于,比如输入是[2,1,2,4,3],对于最后一个元素 3,如何找到元素 4 作为 Next Greater Number。
对于这种需求,常用套路就是将数组长度翻倍:
这样,元素 3 就可以找到元素 4 作为 Next Greater Number 了,而且其他的元素都可以被正确地计算。
有了思路,最简单的实现方式当然可以把这个双倍长度的数组构造出来,然后套用算法模板。但是,我们可以不用构造新数组,而是利用循环数组的技巧来模拟数组长度翻倍的效果。
代码实现
/**
* https://leetcode-cn.com/problems/next-greater-element-ii/
*
* @author xiexu
* @create 2022-01-25 9:15 下午
*/
public class _503_下一个更大元素_II {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] res = new int[n];
Stack<Integer> stack = new Stack<>();
//假设这个数组长度翻倍了
for (int i = 2 * n - 1; i >= 0; i--) {
//索引要求模,其他的和单调栈模板一样
while (!stack.isEmpty() && stack.peek() <= nums[i % n]) {
stack.pop();
}
res[i % n] = stack.isEmpty() ? -1 : stack.peek();
stack.push(nums[i % n]);
}
return res;
}
}
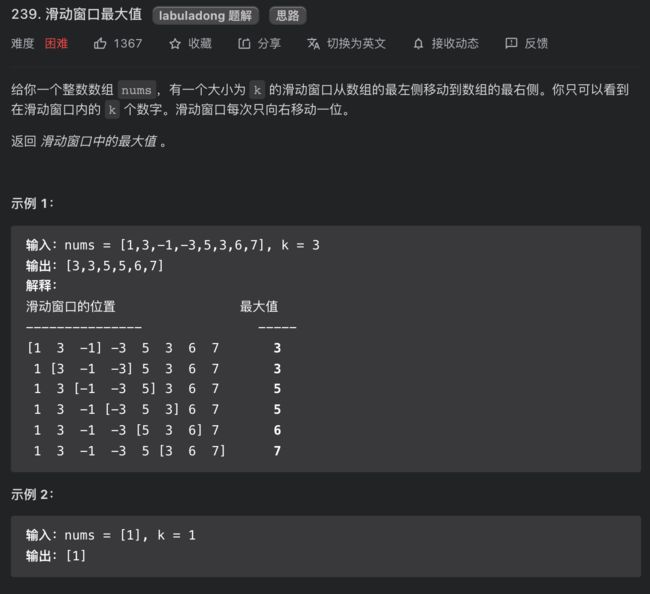
239. 滑动窗口最大值
思路分析
每个窗口前进的时候,要添加一个数同时减少一个数,所以想在 O(1) 的时间得出新的最值,不是那么容易的,需要「单调队列」这种特殊的数据结构来辅助。
一个普通的队列一定有这两个操作:
class Queue {
// enqueue 操作,在队尾加入元素 n
void push(int n);
// dequeue 操作,删除队头元素
void pop();
}
一个「单调队列」的操作也差不多:
class MonotonicQueue {
// 在队尾添加元素 n
void push(int n);
// 返回当前队列中的最大值
int max();
// 队头元素如果是 n,删除它
void pop(int n);
}
当然,这几个 API 的实现方法肯定跟一般的 Queue 不一样,不过我们暂且不管,而且认为这几个操作的时间复杂度都是 O(1),先把这道「滑动窗口」问题的解答框架搭出来:
int[] maxSlidingWindow(int[] nums, int k) {
MonotonicQueue window = new MonotonicQueue();
List<Integer> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (i < k - 1) {
//先把窗口的前 k - 1 填满
window.push(nums[i]);
} else {
// 窗口开始向前滑动
// 移入新元素
window.push(nums[i]);
// 将当前窗口中的最大元素记入结果
res.add(window.max());
// 移出最后的元素
window.pop(nums[i - k + 1]);
}
}
// 将 List 类型转化成 int[] 数组作为返回值
int[] arr = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
arr[i] = res.get(i);
}
return arr;
}
这个思路很简单,能理解吧?下面我们开始重头戏,单调队列的实现。
实现单调队列数据结构
观察滑动窗口的过程就能发现,实现「单调队列」必须使用一种数据结构支持在头部和尾部进行插入和删除,很明显双链表是满足这个条件的。
「单调队列」的核心思路和「单调栈」类似,push方法依然在队尾添加元素,但是要把前面比自己小的元素都删掉:
class MonotonicQueue {
// 双链表,支持头部和尾部增删元素
private LinkedList<Integer> q = new LinkedList<>();
public void push(int n) {
// 将前面小于自己的元素都删除
while (!q.isEmpty() && q.getLast() < n) {
q.pollLast();
}
q.addLast(n);
}
}
你可以想象,加入数字的大小代表人的体重,把前面体重不足的都压扁了,直到遇到更大的量级才停住。
如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个单调递减的顺序,因此我们的max方法可以可以这样写:
public int max() {
// 队头的元素肯定是最大的
return q.getFirst();
}
pop方法在队头删除元素n,也很好写:
public void pop(int n) {
if (n == q.getFirst()) {
q.pollFirst();
}
}
之所以要判断 n == q.getFirst(),是因为我们想删除的队头元素n可能已经被「压扁」了,可能已经不存在了,所以这时候就不用删除了:
至此,单调队列设计完毕,看下完整的单调队列代码:
// 单调队列
class MonotonicQueue {
LinkedList<Integer> q = new LinkedList<>();
// 在队尾添加元素 n
public void push(int n) {
// 将小于 n 的元素全部删除
while (!q.isEmpty() && q.getLast() < n) {
q.pollLast();
}
// 然后将 n 加入尾部
q.addLast(n);
}
// 返回当前队列中的最大值
public int max() {
return q.getFirst();
}
// 队头元素如果是 n,删除它
public void pop(int n) {
if (n == q.getFirst()) {
q.pollFirst();
}
}
}
代码实现
/**
* https://leetcode-cn.com/problems/sliding-window-maximum/
*
* @author xiexu
* @create 2022-01-25 9:51 下午
*/
public class _239_滑动窗口最大值 {
public int[] maxSlidingWindow(int[] nums, int k) {
MonotonicQueue window = new MonotonicQueue();
ArrayList<Integer> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
if (i < k - 1) {
//先填满窗口的前 k - 1 个
window.push(nums[i]);
} else {
// 窗口向前滑动,加入新数字
window.push(nums[i]);
// 记录当前窗口的最大值
res.add(window.max());
// 移出旧数字
window.pop(nums[i - k + 1]);
}
}
// 需要转成 int[] 数组再返回
int[] arr = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
arr[i] = res.get(i);
}
return arr;
}
}
class MonotonicQueue {
LinkedList<Integer> q = new LinkedList<>();
// 在队尾添加元素 n
public void push(int n) {
// 将小于 n 的元素全部删除
while (!q.isEmpty() && q.getLast() < n) {
q.pollLast();
}
// 然后将 n 加入尾部
q.addLast(n);
}
// 返回当前队列中的最大值
public int max() {
return q.getFirst();
}
// 队头元素如果是 n,删除它
public void pop(int n) {
if (n == q.getFirst()) {
q.pollFirst();
}
}
}
316. 去除重复字母
思路分析
题目的要求总结出来有三点:
要求一、要去重。
要求二、去重字符串中的字符顺序不能打乱s中字符出现的相对顺序。
要求三、在所有符合上一条要求的去重字符串中,字典序最小的作为最终结果。
上述三条要求中,要求三可能有点难理解,举个例子。
比如说输入字符串s = "babc",去重且符合相对位置的字符串有两个,分别是"bac"和"abc",但是我们的算法得返回"abc",因为它的字典序更小。
按理说,如果我们想要有序的结果,那就得对原字符串排序对吧,但是排序后就不能保证符合s中字符出现顺序了,这似乎是矛盾的。
其实这里会借鉴前文 单调栈解题框架 中讲到的「单调栈」的思路,没看过也无妨,等会你就明白了。
我们先暂时忽略要求三,用「栈」来实现一下要求一和要求二,至于为什么用栈来实现,后面你就知道了:
String removeDuplicateLetters(String s) {
// 存放去重的结果
Stack<Character> stk = new Stack<>();
// 布尔数组初始值为 false,记录栈中是否存在某个字符
// 输入字符均为 ASCII 字符,所以大小 256 够用了
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
// 如果字符 c 存在栈中,直接跳过
if (inStack[c]) continue;
// 若不存在,则插入栈顶并标记为存在
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.empty()) {
sb.append(stk.pop());
}
// 栈中元素插入顺序是反的,需要 reverse 一下
return sb.reverse().toString();
}
这段代码的逻辑很简单吧,就是用布尔数组inStack记录栈中元素,达到去重的目的,此时栈中的元素都是没有重复的。
如果输入s = "bcabc",这个算法会返回"bca",已经符合要求一和要求二了,但是题目希望要的答案是"abc"对吧。
那我们想一想,如果想满足要求三,保证字典序,需要做些什么修改?
在向栈stk中插入字符'a'的这一刻,我们的算法需要知道,字符'a'的字典序和之前的两个字符'b'和'c'相比,谁大谁小?
如果当前字符'a'比之前的字符字典序小,就有可能需要把前面的字符 pop 出栈,让'a'排在前面,对吧?
那么,我们先改一版代码:
String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
if (inStack[c]) continue;
// 插入之前,和之前的元素比较一下大小
// 如果字典序比前面的小,pop 前面的元素
while (!stk.isEmpty() && stk.peek() > c) {
// 弹出栈顶元素,并把该元素标记为不在栈中
inStack[stk.pop()] = false;
}
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.empty()) {
sb.append(stk.pop());
}
return sb.reverse().toString();
}
这段代码也好理解,就是插入了一个 while 循环,连续 pop 出比当前字符大的栈顶字符,直到栈顶元素比当前元素的字典序还小为止。只是不是有点「单调栈」的意思了?
这样,对于输入s = "bcabc",我们可以得出正确结果"abc"了。
但是,如果我改一下输入,假设s = "bcac",按照刚才的算法逻辑,返回的结果是"ac",而正确答案应该是"bac",分析一下这是怎么回事?
很容易发现,因为s中只有唯一一个'b',即便字符'a'的字典序比字符'b'要小,字符'b'也不应该被 pop 出去。
那问题出在哪里?
我们的算法在stk.peek() > c时才会 pop 元素,其实这时候应该分两种情况:
情况一、如果stk.peek()这个字符之后还会出现,那么可以把它 pop 出去,反正后面还有嘛,后面再 push 到栈里,刚好符合字典序的要求。
情况二、如果stk.peek()这个字符之后不会出现了,前面也说了栈中不会存在重复的元素,那么就不能把它 pop 出去,否则你就永远失去了这个字符。
回到s = "bcac"的例子,插入字符'a'的时候,发现前面的字符'c'的字典序比'a'大,且在'a'之后还存在字符'c',那么栈顶的这个'c'就会被 pop 掉。
while 循环继续判断,发现前面的字符'b'的字典序还是比'a'大,但是在'a'之后再没有字符'b'了,所以不应该把'b'pop 出去。
那么关键就在于,如何让算法知道字符'a'之后有几个'b'有几个'c'呢?
也不难,只要再改一版代码:
public String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();
// 维护一个计数器记录字符串中字符的数量
// 因为输入为 ASCII 字符,大小 256 够用了
int[] count = new int[256];
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i)]++;
}
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
// 每遍历过一个字符,都将对应的计数减一
count[c]--;
// 如果字符 c 存在栈中,直接跳过
if (inStack[c]) {
continue;
}
// 插入之前,和之前的元素比较一下大小
// 如果当前字典序比栈顶的小,pop 栈顶的元素
while (!stk.isEmpty() && stk.peek() > c) {
// 若之后不存在栈顶元素了,则停止 pop
if (count[stk.peek()] == 0) {
break;
}
// 若之后还有,则可以 pop
inStack[stk.pop()] = false;
}
// 若字符c不存在,则插入栈顶并标记为存在
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.isEmpty()) {
sb.append(stk.pop());
}
// 栈中元素插入顺序是反的,需要 reverse 一下
return sb.reverse().toString();
}
我们用了一个计数器count,当字典序较小的字符试图「挤掉」栈顶元素的时候,在count中检查栈顶元素是否是唯一的,只有当后面还存在栈顶元素的时候才能挤掉,否则不能挤掉。
至此,这个算法就结束了,时间空间复杂度都是 O(N)。
你还记得我们开头提到的三个要求吗?我们是怎么达成这三个要求的?
要求一、通过inStack这个布尔数组做到栈stk中不存在重复元素。
要求二、我们顺序遍历字符串s,通过「栈」这种顺序结构的 push/pop 操作记录结果字符串,保证了字符出现的顺序和s中出现的顺序一致。
这里也可以想到为什么要用「栈」这种数据结构,因为先进后出的结构允许我们立即操作刚插入的字符,如果用「队列」的话肯定是做不到的。
要求三、我们用类似单调栈的思路,配合计数器count不断 pop 掉不符合最小字典序的字符,保证了最终得到的结果字典序最小。
当然,由于栈的结构特点,我们最后需要把栈中元素取出后再反转一次才是最终结果。
代码实现
/**
* https://leetcode-cn.com/problems/remove-duplicate-letters/
*
* @author xiexu
* @create 2022-01-26 9:56 上午
*/
public class _316_去除重复字母 {
public String removeDuplicateLetters(String s) {
Stack<Character> stk = new Stack<>();
// 维护一个计数器记录字符串中字符的数量
// 因为输入为 ASCII 字符,大小 256 够用了
int[] count = new int[256];
for (int i = 0; i < s.length(); i++) {
count[s.charAt(i)]++;
}
boolean[] inStack = new boolean[256];
for (char c : s.toCharArray()) {
// 每遍历过一个字符,都将对应的计数减一
count[c]--;
// 如果字符 c 存在栈中,直接跳过
if (inStack[c]) {
continue;
}
// 插入之前,和之前的元素比较一下大小
// 如果当前字典序比栈顶的小,pop 栈顶的元素
while (!stk.isEmpty() && stk.peek() > c) {
// 若之后不存在栈顶元素了,则停止 pop
if (count[stk.peek()] == 0) {
break;
}
// 若之后还有,则可以 pop
// 弹出栈顶元素,并把该元素标记为不在栈中
inStack[stk.pop()] = false;
}
// 若字符c不存在,则插入栈顶并标记为存在
stk.push(c);
inStack[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stk.isEmpty()) {
sb.append(stk.pop());
}
// 栈中元素插入顺序是反的,需要 reverse 一下
return sb.reverse().toString();
}
}
380. O(1) 时间插入、删除和获取随机元素
思路分析
就是说就是让我们实现如下一个类:
class RandomizedSet {
/** 如果 val 不存在集合中,则插入并返回 true,否则直接返回 false */
public boolean insert(int val) {}
/** 如果 val 在集合中,则删除并返回 true,否则直接返回 false */
public boolean remove(int val) {}
/** 从集合中等概率地随机获得一个元素 */
public int getRandom() {}
}
本题的难点在于两点:
1、插入,删除,获取随机元素这三个操作的时间复杂度必须都是 O(1)。
2、getRandom方法返回的元素必须等概率返回随机元素,也就是说,如果集合里面有n个元素,每个元素被返回的概率必须是1/n。
我们先来分析一下:对于插入,删除,查找这几个操作,哪种数据结构的时间复杂度是 O(1)?
HashSet肯定算一个对吧。哈希集合的底层原理就是一个大数组,我们把元素通过哈希函数映射到一个索引上;如果用拉链法解决哈希冲突,那么这个索引可能连着一个链表或者红黑树。
那么请问对于这样一个标准的HashSet,你能否在 O(1) 的时间内实现getRandom函数?
其实是不能的,因为根据刚才说到的底层实现,元素是被哈希函数「分散」到整个数组里面的,更别说还有拉链法等等解决哈希冲突的机制,基本做不到 O(1) 时间等概率随机获取元素。
除了HashSet,还有一些类似的数据结构,比如哈希链表LinkedHashSet,本质上就是哈希表配合双链表,元素存储在双链表中。
但是,LinkedHashSet只是给HashSet增加了有序性,依然无法按要求实现我们的getRandom函数,因为底层用链表结构存储元素的话,是无法在 O(1) 的时间内访问某一个元素的。
根据上面的分析,对于getRandom方法,如果想「等概率」且「在 O(1) 的时间」取出元素,一定要满足:底层用数组实现,且数组必须是紧凑的。
这样我们就可以直接生成随机数作为索引,从数组中取出该随机索引对应的元素,作为随机元素。
但如果用数组存储元素的话,插入,删除的时间复杂度怎么可能是 O(1) 呢?
可以做到!对数组尾部进行插入和删除操作不会涉及数据搬移,时间复杂度是 O(1)。
所以,如果我们想在 O(1) 的时间删除数组中的某一个元素val,可以先把这个元素交换到数组的尾部,然后再pop掉。
交换两个元素必须通过索引进行交换对吧,那么我们需要一个哈希表valToIndex来记录每个元素值对应的索引。
代码实现
/**
* https://leetcode-cn.com/problems/insert-delete-getrandom-o1/
*
* @author xiexu
* @create 2022-01-26 2:00 下午
*/
public class _380_O1时间插入_删除和获取随机元素 {
}
class RandomizedSet {
// 存储元素的值
List<Integer> nums;
// 记录每个元素对应在nums数组中的索引
HashMap<Integer, Integer> valToIndex;
Random random;
public RandomizedSet() {
nums = new ArrayList<>();
valToIndex = new HashMap<>();
random = new Random();
}
/**
* 如果 val 不存在集合中,则插入并返回 true,否则直接返回 false
*/
public boolean insert(int val) {
//若val已存在,不用插入
if (valToIndex.containsKey(val)) {
return false;
}
//若val不存在,插入到nums尾部
//并记录 val 对应的索引值
valToIndex.put(val, nums.size());
nums.add(val);
return true;
}
/**
* 如果 val 在集合中,则删除并返回 true,否则直接返回 false
*/
public boolean remove(int val) {
//若 val 不存在,不用再删除
if (!valToIndex.containsKey(val)) {
return false;
}
//先拿到val的索引
int index = valToIndex.get(val);
//将最后一个元素对应的索引修改为 index
int last = nums.get(nums.size() - 1);
valToIndex.put(last, index);
//交换val和最后一个元素
nums.set(index, last);
nums.set(nums.size() - 1, val);
//在数组中删除元素 val
nums.remove(nums.size() - 1);
//删除元素val对应的索引
valToIndex.remove(val);
return true;
}
/**
* 从集合中等概率地随机获得一个元素
*/
public int getRandom() {
//nextInt(num):随机返回一个值在[0,num)的int类型的整数,包括0但不包括num
return nums.get(random.nextInt(nums.size()));
}
}
710. 黑名单中的随机数
思路分析
给你输入一个正整数N,代表左闭右开区间[0,N),再给你输入一个数组blacklist,其中包含一些「黑名单数字」,且blacklist中的数字都是区间[0,N)中的数字。
现在要求你设计如下数据结构:
class Solution {
// 构造函数,输入参数
public Solution(int N, int[] blacklist) {
}
// 在区间 [0,N) 中等概率随机选取一个元素并返回
// 这个元素不能是 blacklist 中的元素
public int pick() {
}
}
pick函数会被多次调用,每次调用都要在区间[0,N)中「等概率随机」返回一个「不在blacklist中」的整数。
这应该不难理解吧,比如给你输入N = 5, blacklist = [1,3],那么多次调用pick函数,会等概率随机返回 0, 2, 4 中的某一个数字。
而且题目要求,在pick函数中应该尽可能少调用随机数生成函数rand()。
聪明的解法类似上一道题,我们可以将区间[0,N)看做一个数组,然后将blacklist中的元素移到数组的最末尾,同时用一个哈希表进行映射:
根据这个思路,我们可以写出第一版代码(还存在几处错误):
class Solution {
int size; //数组中的有效元素个数
HashMap<Integer, Integer> mapping = new HashMap<>(); //黑名单元素的映射
Random random = new Random();
public Solution(int n, int[] blacklist) {
// 有效数组的元素个数
size = n - blacklist.length;
// 最后一个元素的索引
int last = n - 1;
// 将黑名单中的索引换到最后去
for (int b : blacklist) {
mapping.put(b, last);
last--;
}
}
}
如上图,相当于把黑名单中的数字都交换到了区间[sz, N)中,同时把[0, sz)中的黑名单数字映射到了正常数字。
根据这个逻辑,我们可以写出pick函数:
public int pick() {
// 随机选取一个索引
int index = random.nextInt(size);
// 这个索引如果命中了黑名单,需要被映射到其他位置
if (mapping.containsKey(index)) {
return mapping.get(index);
}
// 若没命中黑名单,则直接返回
return index;
}
这个pick函数已经没有问题了,但是构造函数还有两个问题。
第一个问题,如下这段代码:
int last = n - 1;
// 将黑名单中的索引换到最后去
for (int b : blacklist) {
mapping.put(b, last);
last--;
}
我们将黑名单中的b映射到last,但是我们能确定last不在blacklist中吗?
比如下图这种情况,我们的预期应该是 1 映射到 3,但是错误地映射到 4:
在对mapping[b]赋值时,要保证last一定不在blacklist中,可以如下操作:
class Solution {
int size; //数组中的有效元素个数
HashMap<Integer, Integer> mapping = new HashMap<>(); //黑名单元素的映射
Random random = new Random();
public Solution(int n, int[] blacklist) {
// 有效数组的元素个数
size = n - blacklist.length;
// 先将所有黑名单数字加入 mapping
for (int b : blacklist) {
// 这里赋值多少都可以
// 目的仅仅是把键存进哈希表
// 方便快速判断数字是否在黑名单内
mapping.put(b, 666);
}
// 最后一个元素的索引
int last = n - 1;
for (int b : blacklist) {
// 跳过所有黑名单中的数字
while (mapping.containsKey(last)) {
last--;
}
// 将黑名单中的索引映射到合法数字
mapping.put(b, last);
last--;
}
}
}
第二个问题,如果blacklist中的黑名单数字本身就存在区间[sz, N)中,那么就没必要在mapping中建立映射,比如这种情况:
我们根本不用管 4,只希望把 1 映射到 3,但是按照blacklist的顺序,会把 4 映射到 3,显然是错误的。
我们可以稍微修改一下,写出正确的解法代码:
class Solution {
int size; //数组中的有效元素个数
HashMap<Integer, Integer> mapping = new HashMap<>();
Random random = new Random();
public Solution(int n, int[] blacklist) {
// 最终数组中的元素个数
size = n - blacklist.length;
// 先将所有黑名单数字加入 mapping
for (int b : blacklist) {
// 这里赋值多少都可以
// 目的仅仅是把键存进哈希表
// 方便快速判断数字是否在黑名单内
mapping.put(b, 666);
}
// 最后一个元素的索引
int last = n - 1;
for (int b : blacklist) {
// 如果 b 已经在区间 [size, n)
// 可以直接忽略
if (b >= size) {
continue;
}
// 跳过所有黑名单中的数字
while (mapping.containsKey(last)) {
last--;
}
// 将黑名单中的索引映射到合法数字
mapping.put(b, last);
last--;
}
}
}
代码实现
/**
* https://leetcode-cn.com/problems/random-pick-with-blacklist/
*
* @author xiexu
* @create 2022-01-26 2:23 下午
*/
public class _710_黑名单中的随机数 {
public static void main(String[] args) {
Solution solution = new Solution(5, new int[]{4, 1});
System.out.println(solution.pick());
}
}
class Solution {
int size; //数组中的有效元素个数
HashMap<Integer, Integer> mapping = new HashMap<>(); //黑名单元素的映射
Random random = new Random();
public Solution(int n, int[] blacklist) {
// 有效数组的元素个数
size = n - blacklist.length;
// 先将所有黑名单数字加入 mapping
for (int b : blacklist) {
// 这里赋值多少都可以
// 目的仅仅是把键存进哈希表
// 方便快速判断数字是否在黑名单内
mapping.put(b, 666);
}
// 最后一个元素的索引
int last = n - 1;
for (int b : blacklist) {
// 如果 b 已经在区间 [size, n),相当于已经存在数组的末尾了
// 可以直接忽略
if (b >= size) {
continue;
}
// 跳过所有黑名单中的数字
while (mapping.containsKey(last)) {
last--;
}
// 将黑名单中的索引映射到合法数字
mapping.put(b, last);
last--;
}
}
public int pick() {
// 随机选取一个索引
int index = random.nextInt(size);
// 这个索引如果命中了黑名单,需要被映射到其他位置
if (mapping.containsKey(index)) {
return mapping.get(index);
}
// 若没命中黑名单,则直接返回
return index;
}
}
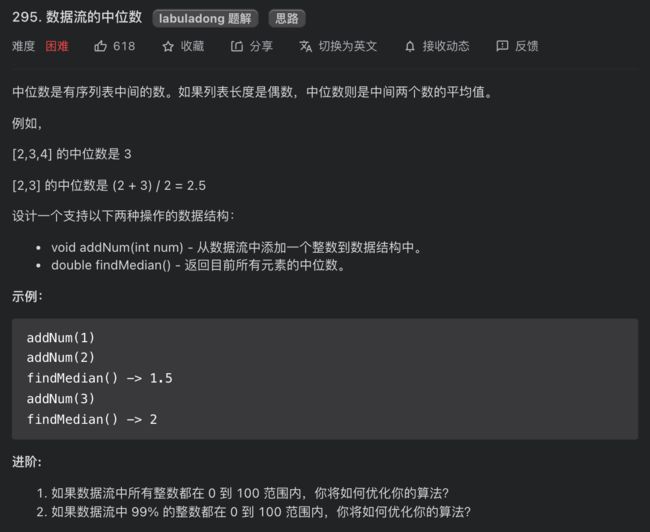
295. 数据流的中位数
思路分析
我们必然需要有序数据结构,本题的核心思路是使用两个优先级队列。
中位数是有序数组最中间的元素算出来的对吧,我们可以把「有序数组」抽象成一个倒三角形,宽度可以视为元素的大小,那么这个倒三角的中部就是计算中位数的元素对吧:
然后我把这个大的倒三角形从正中间切成两半,变成一个小倒三角和一个梯形,这个小倒三角形相当于一个从小到大的有序数组,这个梯形相当于一个从大到小的有序数组。
中位数就可以通过小倒三角和梯形顶部的元素算出来对吧?嗯,你联想到什么了没有?它们能不能用优先级队列表示?小倒三角不就是个大顶堆嘛,梯形不就是个小顶堆嘛,中位数可以通过它们的堆顶元素算出来。
梯形虽然是小顶堆,但其中的元素是较大的,我们称其为large,倒三角虽然是大顶堆,但是其中元素较小,我们称其为small。
当然,这两个堆需要算法逻辑正确维护,才能保证堆顶元素是可以算出正确的中位数,我们很容易看出来,两个堆中的元素之差不能超过 1。
因为我们要求中位数嘛,假设元素总数是n,如果n是偶数,我们希望两个堆的元素个数是一样的,这样把两个堆的堆顶元素拿出来求个平均数就是中位数;如果n是奇数,那么我们希望两个堆的元素个数分别是n/2 + 1和n/2,这样元素多的那个堆的堆顶元素就是中位数。
根据这个逻辑,我们可以直接写出findMedian函数的代码:
class MedianFinder {
private PriorityQueue<Integer> large;
private PriorityQueue<Integer> small;
public MedianFinder() {
// 小顶堆
large = new PriorityQueue<>();
// 大顶堆
small = new PriorityQueue<>((a, b) -> {
return b - a;
});
}
public double findMedian() {
// 如果元素不一样多,多的那个堆的堆顶元素就是中位数
if (large.size() < small.size()) {
return small.peek();
} else if (large.size() > small.size()) {
return large.peek();
}
// 如果元素一样多,两个堆堆顶元素的平均数是中位数
return (large.peek() + small.peek()) / 2.0;
}
public void addNum(int num) {
// 后文实现
}
}
现在的问题是,如何实现addNum方法,维护「两个堆中的元素之差不能超过 1」这个条件呢?
这样行不行?每次调用addNum函数的时候,我们比较一下large和small的元素个数,谁的元素少我们就加到谁那里,如果它们的元素一样多,我们默认加到large里面:
// 有缺陷的代码实现
public void addNum(int num) {
if (small.size() >= large.size()) {
large.offer(num);
} else {
small.offer(num);
}
}
看起来好像没问题,但是跑一下就发现问题了,比如说我们这样调用:
addNum(1),现在两个堆元素数量相同,都是 0,所以默认把 1 添加进large堆。
addNum(2),现在large的元素比small的元素多,所以把 2 添加进small堆中。
addNum(3),现在两个堆都有一个元素,所以默认把 3 添加进large中。
调用findMedian,预期的结果应该是 2,但是实际得到的结果是 1。
问题很容易发现,看下当前两个堆中的数据:
抽象点说,我们的梯形和小倒三角都是由原始的大倒三角从中间切开得到的,那么梯形中的最小宽度要大于等于小倒三角的最大宽度,这样它俩才能拼成一个大的倒三角对吧?
也就是说,不仅要维护large和small的元素个数之差不超过 1,还要维护large堆的堆顶元素要大于等于small堆的堆顶元素。
维护large堆的元素大小整体大于small堆的元素是本题的难点,不是一两个 if 语句能够正确维护的,而是需要如下技巧:
// 正确的代码实现
public void addNum(int num) {
if (small.size() >= large.size()) {
small.offer(num);
large.offer(small.poll());
} else {
large.offer(num);
small.offer(large.poll());
}
}
简单说,想要往large里添加元素,不能直接添加,而是要先往small里添加,然后再把small的堆顶元素加到large中;向small中添加元素同理。
为什么呢,稍加思考可以想明白,假设我们准备向
large中插入元素:
- 如果插入的
num小于small的堆顶元素,那么我们把num留在small堆里,为了保证两个堆的元素数量之差不大于 1,作为交换,把small堆顶的元素再插入到large堆里。 - 如果插入的
num大于large的堆顶元素,那么我们把num留在large的堆里,为了保证两个堆的元素数量之差不大于 1,作为交换,把large堆顶的元素再插入到small堆里。 - 这样就巧妙地保证了
large堆整体大于small堆,且两个堆的元素之差不超过 1,那么中位数就可以通过两个堆的堆顶元素快速计算了。
至此,整个算法就结束了,addNum方法时间复杂度 O(logN),findMedian方法时间复杂度 O(1)。
代码实现
/**
* https://leetcode-cn.com/problems/find-median-from-data-stream/
*
* @author xiexu
* @create 2022-01-28 1:02 下午
*/
public class _295_数据流的中位数 {
}
class MedianFinder {
private PriorityQueue<Integer> large; //小顶堆
private PriorityQueue<Integer> small; //大顶堆
public MedianFinder() {
//小顶堆
large = new PriorityQueue<>();
//大顶堆
small = new PriorityQueue<>((a, b) -> {
return b - a;
});
}
// 添加一个数字
public void addNum(int num) {
if (small.size() >= large.size()) {
small.offer(num);
large.offer(small.poll());
} else {
large.offer(num);
small.offer(large.poll());
}
}
// 计算当前添加的所有数字的中位数
public double findMedian() {
// 如果元素不一样多,多的那个堆的堆顶元素就是中位数
if (large.size() < small.size()) {
return small.peek();
} else if (large.size() > small.size()) {
return large.peek();
}
// 如果元素一样多,两个堆堆顶元素的平均数是中位数
return (large.peek() + small.peek()) / 2.0;
}
}