NNDL 实验二 pytorch入门
文章目录
一. 概念:张量、算子
1、张量
2、算子
二. 使用pytorch实现张量运算
1.2 张量
1.2.1 创建张量
1.2.2 张量的属性
1.2.4 张量的访问
1.2.5 张量的运算
三. 数据预处理
实验体会

一. 概念:张量、算子
抱歉各位可能有点废话,但是真的查了好多资料,实在不想浪费了
1、张量
张量的概念有很多种,首先我们来看一下pytorch官方给出的定义:
Tensors are a specialized data structure that are very similar to arrays and matrices.In PyTorch, we use tensors to encode the inputs and outputs of a model, as well as the model’s parameters.
翻译过来就是:
张量是一种特殊的数据结构,与数组和矩阵非常相似。在PyTorch中,我们使用张量对模型的输入和输出以及模型的参数进行编码。
并且提到:
Tensors are similar toNumPy’sndarrays, except that tensors can run on GPUs or other hardware accelerators. In fact, tensors andNumPy arrays can often share the same underlying memory, eliminating the need to copy data (seeBridge with NumPy). Tensorsare also optimized for automatic differentiation (we’ll see more about that later in theAutogradsection). If you’re familiar with ndarrays, you’ll be right at home with the Tensor API. If not, follow along!
这一大段的主要意思是张量与numpy数组的区别就是张量可以在GPU上运行,其他的几乎相同。
在看一下网上大佬们的解析之后跟可以理解到,张量主要通过三个要素来确定:
1、轴的个数(阶)。例如,3D 张量有 3 个轴,矩阵有 2 个轴。这在 Numpy 等 Python 库中也叫张量的 ndim 。
2、形状。这是一个整数元组,表示张量沿每个轴的维度大小(元素个数)。例如,前面矩阵示例的形状为 (3, 5) ,3D 张量示例的形状为 (3, 3, 5) 。向量的形状只包含一个元素,比如 (5,) ,而标量的形状为空,即 () 。(张量的形状)
3、数据类型(在 Python 库中通常叫作 dtype )。这是张量中所包含数据的类型,例如,张量的类型可以是 float32 、 uint8 、 float64 等。在极少数情况下,你可能会遇到字符( char )张量。注意:Numpy(以及大多数其他库)中不存在字符串张量,因为张量存储在预先分配的连续内存段中,而字符串的长度是可变的,无法用这种方式存储。
我感觉,张量这一概念的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。可能咱们对矩阵很熟悉,它是二维张量。张量是矩阵向任意维度的推广[注意,张量的维度(dimension)通常叫作轴(axis)]。
关于张量的维度,可以由下面几张图来表示
2、算子
英语的算子是Operator,含义为操作、运算等等。
汉语采用算子作为翻译词,可能与算筹有关。
算子可以理解为,把一个函数变成另一个函数的东西。
函数是从数到数的映射。
泛函是从函数到数的映射。
算子是从函数到函数的映射。
当然,有的时候这几个词可以混用,比如可以可以把数当作常函数,那么普通的函数也可以看作泛函或算子;再比如考虑从算子到算子的映射,你仍然可以叫它算子。
具体地讲,比如微分算子(或者叫求导算子)等等等
我认为,在深度学习中深度学习算法由一个个计算单元组成,我们称这些计算单元为算子(Operator,简称OP)。在网络模型中,算子对应层中的计算逻辑,例如:卷积层(Convolution Layer)是一个算子;全连接层(Fully-connected Layer, FC layer)中的权值求和过程,是一个算子。
二. 使用pytorch实现张量运算
1.2 张量
1.2.1 创建张量
1.2.1.1 指定数据创建张量
# coding=gbk
import torch
#创建以为Tensor
x = torch.arange(12) #也是创建以为数组,这个是按序分布的,这个不包括最后一个数
y=torch.tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) #这个是指定的一维数组
print(x)
print(y)
运行结果为 :
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
上边的coding是规定解码方式,要不在pycahrm写注释可能报错,是最好注意这一点。
.arange(12) #也是创建以为数组,这个是按序分布的,这个不包括最后一个数
.tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) #这个是指定的一维数组。这个函数是输入的元素是啥类型,它输出就是啥类型
#创建二位Tensor
x=torch.tensor([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]]) #创建指定张量
print(x)运行结果为:
tensor([[1., 2., 3.],
[4., 5., 6.]])
# 创建多维Tensor
ndim_3_Tensor = torch.tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)运行结果为:
tensor([[[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10]],[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
从后两个可以看出,它是以来'[]'区分 是几维,哪个属于哪一维的,可以从数开头的[来确定是几维。
1.2.1.2 指定形状创建
#创建指定形状的张量
m, n = 2, 3
# 使用paddle.zeros创建数据全为0,形状为[m, n]的Tensor
zeros_Tensor = torch.zeros([m, n])
# 使用paddle.ones创建数据全为1,形状为[m, n]的Tensor
ones_Tensor = torch.ones([m, n])
# 使用paddle.full创建数据全为指定值,形状为[m, n]的Tensor,这里我们指定数据为10
full_Tensor = torch.full([m, n], 10)
print('zeros_Tensor:',zeros_Tensor)
print('ones_Tensor:',ones_Tensor)
print('full_Tensor:',full_Tensor)运行结果为:
zeros_Tensor: tensor([[0., 0., 0.],
[0., 0., 0.]])
ones_Tensor: tensor([[1., 1., 1.],
[1., 1., 1.]])
full_Tensor: tensor([[10, 10, 10],
[10, 10, 10]])
这几个函数在规定形状时,要注意形状是一个参数,要拿[]括起来,要不然可能会报错
1.2.1.3 指定区间创建
#指定区间创建
# 使用paddle.arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
arange_Tensor = torch.arange(start=1, end=5, step=1) #不包括结尾
# 使用paddle.arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
range_Tensor = torch.range(start=1, end=5, step=1) #包括结尾
# 使用paddle.linspace创建以元素个数num均匀分隔数值区间[start, stop]的Tensor
linspace_Tensor = torch.linspace(start=1, end=5, steps=5)
print('arange Tensor: ', arange_Tensor)
print('range Tensor: ', range_Tensor)
print('linspace Tensor: ', linspace_Tensor)运行结果为:
arange Tensor: tensor([1, 2, 3, 4])
range Tensor: tensor([1., 2., 3., 4., 5.])
linspace Tensor: tensor([1., 2., 3., 4., 5.])
这三个方法,分别是
·torch.arange()是不包含结尾的,为左闭右开,也就是不包含右边的最后一个数,[1,5)。
·torch.range是包含结尾的,为左闭右闭,也就是包含右边的最后一个数,[1,5]。这个方法会报一个警告也就是
UserWarning: torch.range is deprecated and will be removed in a future release because its behavior is inconsistent with Python's range builtin. Instead, use torch.arange, which produces values in [start, end).
range_Tensor = torch.range(start=1, end=5, step=1) #包括结尾
这是这个方法要被弃用了,所以大家不要担心
·torch.linspace(),这个方法也是左闭右闭的,但是这个方法和前面的不太一样,它这里的步长其实和前面的不是一个意思,linspace中的steps与咱们上面两个理解的step不同,steps就是将(start, end)分成包含start和end的多少个数,steps是多少,返回的tensor中就有多少个元素
1.2.2 张量的属性
1.2.2.1 张量的形状
#张量的形状
ndim_4_Tensor = torch.ones([2, 3, 4, 5])
print("Number of dimensions:", ndim_4_Tensor.dim()) #此处ndim=dim(),都是输出向量的维度
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])
print('Number of elements in Tensor: ', ndim_4_Tensor.numel())运行结果为:
Number of dimensions: 4
Shape of Tensor: torch.Size([2, 3, 4, 5])
Elements number along axis 0 of Tensor: 2
Elements number along the last axis of Tensor: 5
Number of elements in Tensor: 120
.din()=.ndim,这两个方法是等价的。
shape[n],这个直观理解就是n是几就是第几维上有几个元素。说直观点就是n是几就数到几,看那个数是多少
.numel是统计总共有多少个元素
1.2.2.2 形状的改变
# 定义一个shape为[3,2,5]的三维Tensor
ndim_3_Tensor = torch.tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]],
[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]]])
print("the shape of ndim_3_Tensor:", ndim_3_Tensor.shape)
# torch.reshape 可以保持在输入数据不变的情况下,改变数据形状。这里我们设置reshape为[2,5,3]
reshape_Tensor = torch.reshape(ndim_3_Tensor, [2, 5, 3]) #此时有参数可以为-1,因为-1位置的参数可以由系统计算得出,0是复制对应维度
print("After reshape:", reshape_Tensor)运行结果为:
the shape of ndim_3_Tensor: torch.Size([3, 2, 5])
After reshape: tensor([[[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12],
[13, 14, 15]],[[16, 17, 18],
[19, 20, 21],
[22, 23, 24],
[25, 26, 27],
[28, 29, 30]]])
使用reshape时存在一些技巧,比如:
- -1表示这个维度的值是从张量的元素总数和剩余维度推断出来的。因此,有且只有一个维度可以被设置为-1。
- 0表示实际的维数是从张量的对应维数中复制出来的,因此shape中0所对应的索引值不能超过张量的总维度。
1.2.2.3 张量的数据类型
# 使用torch.tensor通过已知数据来创建一个Tensor
print("Tensor dtype from Python integers:", torch.tensor(1).dtype)
print("Tensor dtype from Python floating point:", torch.tensor(1.0).dtype)运行结果为:
Tensor dtype from Python integers: torch.int64
Tensor dtype from Python floating point: torch.float32
pytorch只能有这八种类型,并且规定类型时只能严格用这八个,不能只写int,经过尝试之后会报错。
dtype:张量的数据类型,分成浮点,整型和布尔三大类,共9种数据类型,如下表所示(引自pytorch官网),其中32位浮点和64位整型最为常用。图像预处理结果默认:torch.float32,图像标签默认:torch.int64.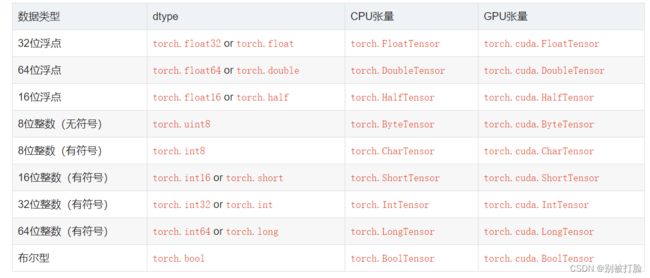
1.2.2.4 张量的设备位置
# 创建CPU上的Tensor
cpu_Tensor = torch.tensor(1, device='cpu:0')
# 通过Tensor.place查看张量所在设备位置
print('cpu Tensor: ', cpu_Tensor.device)
# 创建GPU上的Tensor
gpu_Tensor = torch.tensor(1, device='cuda') #可以用to方法来回转化
print('gpu Tensor: ', gpu_Tensor.device)
# 创建固定内存上的Tensor
pin_memory_Tensor = torch.tensor(1, pin_memory=True) #会影响电脑运行速度
print('pin memory Tensor: ', pin_memory_Tensor.device)运行结果为:
cpu Tensor: cpu
gpu Tensor: cuda:0
pin memory Tensor: cpu
正常情况下,常规的是现在cpu上生成张量,然后判断是否有GPU,若有用to方法将它转到GPU上,也可以直接在GPU上生成,但是这样通用不太好。
pin_memory=True,是在,固定内存上存储,但是这个要注意定义太多会影响运行速度。
1.2.3 张量与Numpy数组转换
ndim_1_Tensor = torch.tensor([1., 2.])
# 将当前 Tensor 转化为 numpy.ndarray
print('Tensor to convert: ', ndim_1_Tensor.numpy())运行结果为:
Tensor to convert: [1. 2.]
.numpy() .tolist() .tensor()可以实现转化numpy、tensor、list之间互相转化
1.2.4 张量的访问
1.2.4.1 索引和切片
# 定义1个一维Tensor
ndim_1_Tensor = torch.tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
print("Origin Tensor:", ndim_1_Tensor)
print("First element:", ndim_1_Tensor[0])
print("Last element:", ndim_1_Tensor[-1])
print("All element:", ndim_1_Tensor[:])
print("Before 3:", ndim_1_Tensor[:3])
print("Interval of 3:", ndim_1_Tensor[::3])
print("Reverse:", torch.flip(ndim_1_Tensor,dims=[0])) #pytorch没有复数步长,故无法通过切片操作达到逆序输出运行结果为:
Origin Tensor: tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
First element: tensor(0)
Last element: tensor(8)
All element: tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
Before 3: tensor([0, 1, 2])
Interval of 3: tensor([0, 3, 6])
Reverse: tensor([8, 7, 6, 5, 4, 3, 2, 1, 0])
我们可以通过索引或切片方便地访问或修改张量。与Numpy索引规则,具有以下特点:
- 基于0−n0−n的下标进行索引,如果下标为负数,则从尾部开始计算。
- 通过冒号“:”分隔切片参数start:stop:step来进行切片操作,也就是访问start到stop范围内的部分元素并生成一个新的序列。其中start为切片的起始位置,stop为切片的截止位置,step是切片的步长,这三个参数均可缺省。
同时注意唯一的不同是pytorch没有负数步长,所以会报错,所以可以用torch.flip(ndim_1_Tensor,dims=[0])直接将张量逆序再输出。但是TensorFlow和numpy都有负数的步长。
1.2.4.2 访问张量
# 定义1个二维Tensor
ndim_2_Tensor = torch.tensor([[0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor)
print("First row:", ndim_2_Tensor[0])
print("First row:", ndim_2_Tensor[0, :])
print("First column:", ndim_2_Tensor[:, 0])
print("Last column:", ndim_2_Tensor[:, -1])
print("All element:", ndim_2_Tensor[:])
print("First row and second column:", ndim_2_Tensor[0, 1])运行结果为:
Origin Tensor: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
First row: tensor([0, 1, 2, 3])
First row: tensor([0, 1, 2, 3])
First column: tensor([0, 4, 8])
Last column: tensor([ 3, 7, 11])
All element: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
First row and second column: tensor(1)
注意-1代表的是 列数从右往左数第一个,这个切边与索引与numpy一样,只是注意没有负数的步长。
1.2.4.3 修改张量
# 定义1个二维Tensor
ndim_2_Tensor = torch.ones(size=(2,3),dtype=torch.float32)
print('Origin Tensor: ', ndim_2_Tensor)
# 修改第1维为0
ndim_2_Tensor[0] = 0
print('change Tensor: ', ndim_2_Tensor)
# 修改第1维为2.1
ndim_2_Tensor[0:1] = 2.1
print('change Tensor: ', ndim_2_Tensor)
# 修改全部Tensor
ndim_2_Tensor[...] = 3
print('change Tensor: ', ndim_2_Tensor)运行结果为:
Origin Tensor: tensor([[1., 1., 1.],
[1., 1., 1.]])
change Tensor: tensor([[0., 0., 0.],
[1., 1., 1.]])
change Tensor: tensor([[2.1000, 2.1000, 2.1000],
[1.0000, 1.0000, 1.0000]])
change Tensor: tensor([[3., 3., 3.],
[3., 3., 3.]])
这个注意“...”这个用法是所有的意思,tensor[...,1] 表示的就是所有行,第一列,在列上用“...”用法与在行上用一致,其他的与numpy的切边与索引的方式一致
同时注意之前说过的问题,不能直接用int等定义,要严格的按pytorch的规定,torch.dtype
1.2.5 张量的运算
1.2.5.1 数学运算
# 定义两个Tensor
x = torch.tensor([[1.1, 2.2], [3.3, 4.4]], dtype=torch.float64)
y = torch.tensor([[5.5, 6.6], [7.7, 8.8]], dtype=torch.float64)
# 第一种调用方法,paddle.add逐元素相加算子,并将各个位置的输出元素保存到返回结果中
print('Method 1: ', torch.add(x, y))
# 第二种调用方法
print('Method 2: ', x.add(y))运行结果为:
Method 1: tensor([[ 6.6000, 8.8000],
[11.0000, 13.2000]], dtype=torch.float64)
Method 2: tensor([[ 6.6000, 8.8000],
[11.0000, 13.2000]], dtype=torch.float64)
PyTorch算术函数包含简单的加减乘除运算: add(),subtract(),multiply() 和 divide()。
算术运算后得到的结果依然是是相同维度的数组。
Tensor求和以及按索引求和:torch.sum() torch.Tensor.indexadd()
Tensor元素乘积:torch.prod(input)
对Tensor求均值、方差、极值:
torch.mean() torch.var()
torch.max() torch.min()
最后还有在NLP领域经常用到的:
求Tensor的平方根倒数、线性插值、双曲正切
torch.rsqrt(input) torch.lerp(star,end,weight)
torch.tanh(input, out=None)
这是一些常用的运算函数
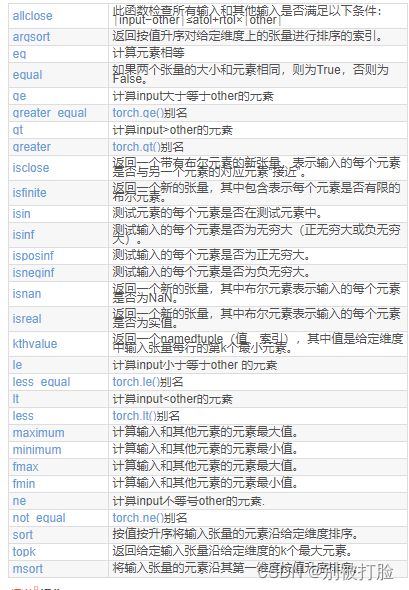
1.2.5.2 逻辑运算
x = torch.tensor([[1.1, 2.2], [3.3, 4.4]], dtype=torch.float64)
y = torch.tensor([[5.5, 6.6], [7.7, 8.8]], dtype=torch.float64)
print(x.isfinite()) # 判断Tensor中元素是否是有限的数字,即不包括inf与nan
print(x.equal(y)) # 判断两个Tensor的全部元素是否相等,并返回形状为[1]的布尔类Tensor
print(x.eq(y)) # 判断两个Tensor的每个元素是否相等,并返回形状相同的布尔类Tensor
print(x.not_equal(y)) # 判断两个Tensor的每个元素是否不相等
print(x.lt(y)) # 判断Tensor x的元素是否小于Tensor y的对应元素 #less的别名
print(x.less_equal(y)) # 判断Tensor x的元素是否小于或等于Tensor y的对应元素 #le的别名
print(x.gt(y)) # 判断Tensor x的元素是否大于Tensor y的对应元素 #greater的别名
print(x.greater_equal(y)) # 判断Tensor x的元素是否大于或等于Tensor y的对应元素 #ge的别名
print(x.allclose(y)) # 判断两个Tensor的全部元素是否接近运行结果为:
tensor([[True, True],
[True, True]])
False
tensor([[False, False],
[False, False]])
tensor([[True, True],
[True, True]])
tensor([[True, True],
[True, True]])
tensor([[True, True],
[True, True]])
tensor([[False, False],
[False, False]])
tensor([[False, False],
[False, False]])
False
1.2.5.3 矩阵运算
x = torch.tensor([[1.1, 2.2], [3.3, 4.4]], dtype=torch.float64)
y = torch.tensor([[5.5, 6.6], [7.7, 8.8]], dtype=torch.float64)
print(x.T) # 矩阵转置
print(x.transpose(1, 0)) # 交换第 0 维与第 1 维的顺序
print(x.norm('fro')) # 矩阵的弗罗贝尼乌斯范数
print(x.dist(y, p=2)) # 矩阵(x-y)的2范数
print(x.matmul(y)) # 矩阵乘法 #这个若矩阵维度不相同,也能相乘运行结果为:
tensor([[1.1000, 3.3000],
[2.2000, 4.4000]], dtype=torch.float64)
tensor([[1.1000, 3.3000],
[2.2000, 4.4000]], dtype=torch.float64)
tensor(6.0249, dtype=torch.float64)
tensor(8.8000, dtype=torch.float64)
tensor([[22.9900, 26.6200],
[52.0300, 60.5000]], dtype=torch.float64)
注意torch.transpose(Tensor,dim0,dim1)是pytorch中的ndarray矩阵进行转置的操作
transpose()一次只能在两个维度间进行转置(也可以理解为维度转换)
tranpose()也能实现矩阵转置但是.T更方便。
.matmul()需要符合矩阵运算的规则。
1.2.5.4 广播机制
# 当两个Tensor的形状一致时,可以广播
x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 4))
z = x + y
print('broadcasting with two same shape tensor: ', z.shape)
x = torch.ones((2, 3, 1, 5))
y = torch.ones((3, 4, 1))
# 从后往前依次比较:
# 第一次:y的维度大小是1
# 第二次:x的维度大小是1
# 第三次:x和y的维度大小相等,都为3
# 第四次:y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('broadcasting with two different shape tensor:', z.shape)
'''
x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 6))
z = x + y
'''运行结果为:
broadcasting with two same shape tensor: torch.Size([2, 3, 4])
broadcasting with two different shape tensor: torch.Size([2, 3, 4, 5])
定义:
如果一个PyTorch操作支持广播,则其Tensor参数可以自动扩展为相等大小(不需要复制数据)。通常情况下,小一点的数组会被 broadcast 到大一点的,这样才能保持大小一致。
如果遵守以下规则,则两个tensor是“可广播的”:
1、每个tensor至少有一个维度;
2、遍历tensor所有维度时,从末尾随开始遍历,两个tensor存在下列情况:
1.tensor维度相等。
2.tensor维度不等且其中一个维度为1。
3.tensor维度不等且其中一个维度不存在。
如果两个tensor是“可广播的”,则计算过程遵循下列规则:
1、如果两个tensor的维度不同,则在维度较小的tensor的前面增加维度,使它们维度相等。
2、对于每个维度,计算结果的维度值取两个tensor中较大的那个值。
3、两个tensor扩展维度的过程是将数值进行复制。
但是就像我''' ''' 的那部分。那部分不符合传播机制的要求,故无法传播要特别注意
三. 数据预处理
1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv
import pandas as pd这个要单独说一下,是因为,之前我就说了,我更喜欢用pandas来读带标签的数据,并且read_csv不仅csv可以读,txt也可以读,所以比较方便。
house_tiny=pd.read_csv('house_tiny.csv',encoding='gbk')
boston_house_prices=pd.read_csv('boston_house_prices.csv',encoding='gbk')
Iris = pd.read_csv('Iris.csv', encoding='gbk')
print(house_tiny)
print(boston_house_prices)
print(Iris)运行结果为:
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
CRIM ZN INDUS CHAS NOX ... RAD TAX PTRATIO LSTAT MEDV
0 0.00632 18.0 2.31 0 0.538 ... 1 296 15.3 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 ... 2 242 17.8 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 ... 2 242 17.8 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 ... 3 222 18.7 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 ... 3 222 18.7 5.33 36.2
.. ... ... ... ... ... ... ... ... ... ... ...
501 0.06263 0.0 11.93 0 0.573 ... 1 273 21.0 9.67 22.4
502 0.04527 0.0 11.93 0 0.573 ... 1 273 21.0 9.08 20.6
503 0.06076 0.0 11.93 0 0.573 ... 1 273 21.0 5.64 23.9
504 0.10959 0.0 11.93 0 0.573 ... 1 273 21.0 6.48 22.0
505 0.04741 0.0 11.93 0 0.573 ... 1 273 21.0 7.88 11.9[506 rows x 13 columns]
Id SepalLengthCm ... PetalWidthCm Species
0 1 5.1 ... 0.2 Iris-setosa
1 2 4.9 ... 0.2 Iris-setosa
2 3 4.7 ... 0.2 Iris-setosa
3 4 4.6 ... 0.2 Iris-setosa
4 5 5.0 ... 0.2 Iris-setosa
.. ... ... ... ... ...
145 146 6.7 ... 2.3 Iris-virginica
146 147 6.3 ... 1.9 Iris-virginica
147 148 6.5 ... 2.0 Iris-virginica
148 149 6.2 ... 2.3 Iris-virginica
149 150 5.9 ... 1.8 Iris-virginica[150 rows x 6 columns]
读的时候要注意解码方式,enconding就是解码方式,并且要把数据复制到根目录下这样不用考虑路径问题,这个数据NAN表示的数据缺失
2. 处理缺失值
inputs, outputs = house_tiny.iloc[:, 0:2], house_tiny.iloc[:, 2]
print(inputs)
print(outputs)
inputs = inputs.fillna(inputs.mean())
inputs = pd.get_dummies(inputs, dummy_na=True)
data=pd.concat([inputs,outputs],axis=1) #inputs['Price']=house_tiny['Price']
print(data)
运行结果为:
NumRooms Alley
0 NaN Pave
1 2.0 NaN
2 4.0 NaN
3 NaN NaN
0 127500
1 106000
2 178100
3 140000
Name: Price, dtype: int64NumRooms Alley_Pave Alley_nan Price
0 3.0 1 0 127500
1 2.0 0 1 106000
2 4.0 0 1 178100
3 3.0 0 1 140000
-
dropna:根据每个标签的值是否是缺失数据来筛选轴标签,并根据允许丢失的数据量来确定阈值
-
fillna:用某些值填充缺失的数据或使用插值方法(如“ffill”或“bfill”)。
-
isnull:返回表明哪些值是缺失值的布尔值
-
notnull:isnull的反作用函数
这几个函数够可以用来处理缺失值但是,常用还是fillna,所以重点说一下fillna的用法
fillna(value=None, method=None, axis=None, inplace=False, limit=None, downcast=None, **kwargs)
value:用于填充的空值的值。
method: {'backfill', 'bfill', 'pad', 'ffill', None}, default None。定义了填充空值的方法, pad / ffill表示用前面行/列的值,填充当前行/列的空值, backfill / bfill表示用后面行/列的值,填充当前行/列的空值。
axis:轴。0或'index',表示按行删除;1或'columns',表示按列删除。
inplace:是否原地替换。布尔值,默认为False。如果为True,则在原DataFrame上进行操作,返回值为None。
这里必须要说一下的是,我写注释的那是连接起来的部分,我用的是conact函数,但是更简便的是用pandas创建列的方法,但是我一开始用的是outputs,所以有问题,我就用了conact,但是为什么又问实在是有点不太明白。
3. 转换为张量格式
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
print(X, y)
Iris['Species'].replace({'Iris-setosa':1,'Iris-versicolor':2,'Iris-virginica':3},inplace=True)
Iris=torch.tensor(Iris.values) #.values方法不能转化带有字符串的
print(Iris)
boston_house=torch.tensor(boston_house_prices.values)
print(boston_house)运行结果为:
tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64) tensor([127500, 106000, 178100, 140000])tensor([[1.0000e+00, 5.1000e+00, 3.5000e+00, 1.4000e+00, 2.0000e-01, 1.0000e+00],
[2.0000e+00, 4.9000e+00, 3.0000e+00, 1.4000e+00, 2.0000e-01, 1.0000e+00],
[3.0000e+00, 4.7000e+00, 3.2000e+00, 1.3000e+00, 2.0000e-01, 1.0000e+00],
[4.0000e+00, 4.6000e+00, 3.1000e+00, 1.5000e+00, 2.0000e-01, 1.0000e+00],
[5.0000e+00, 5.0000e+00, 3.6000e+00, 1.4000e+00, 2.0000e-01, 1.0000e+00],
[6.0000e+00, 5.4000e+00, 3.9000e+00, 1.7000e+00, 4.0000e-01, 1.0000e+00],
[1.5000e+02, 5.9000e+00, 3.0000e+00, 5.1000e+00, 1.8000e+00, 3.0000e+00]],
dtype=torch.float64)tensor([[6.3200e-03, 1.8000e+01, 2.3100e+00, ..., 1.5300e+01, 4.9800e+00,
2.4000e+01],
[2.7310e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 9.1400e+00,
2.1600e+01],
[2.7290e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 4.0300e+00,
3.4700e+01],
...,
[6.0760e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 5.6400e+00,
2.3900e+01],
[1.0959e-01, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 6.4800e+00,
2.2000e+01],
[4.7410e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 7.8800e+00,
1.1900e+01]], dtype=torch.float64)
鸢尾花那个有点多就取得开头和结尾
这里注意一点,.values无法转换字符串,要是直接转换会报错,会提示可以转换的有啥,其中不包括字符串,所以要用1,2,3,来替换她,用的是replace方法,这个方法还必须用字典的那种才可以,可以看看我写的代码。
实验体会
第一部分,是明确了,张量,算子的概念,之前根本没考虑过明确的概念,就只是直接用,现在终于明确了概念,张量看了好多文献有点明白了,但是算子的概念在pytorch的官方文献上是没有的,所有又去看了好多,还是有点不太明白,感谢老师,感觉明白概念以后,看好多文献才更加明白了,概念是一切的基础。
第二部分,是对照了两本书把paddlepaddle的代码,改成pytorch的代码,这部分明白了好多以前有点模糊的用法吗,更加系统了,之前是用着啥查啥,这次之后更加系统了更加清楚了,尤其是对张量设备位置的代码,以前都是用固定的语句,就是判断的那种,有GPU再转化过去,尤其是固定内存那还是不太明白,传播机制以前就是认为它叫自动填充,但是这次之后明白了它的使用条件。
第三部分是之前我说过的预处理部分,我用的pandas但是,再处理缺失值之后,连接的那,我用的是conact函数,但是更简便的是用pandas创建列的方法,但是我一开始用的是outputs,所以有问题,inputs['Price']=outputs['Price']是报错的,我输出之后不知道为什么outputs是那样的,我就用了conact,但是为什么是这样,实在是有点不太明白,之后就是正常的转化。
最后,感觉这次实验学到了很多,谢谢老师