吴恩达机器学习笔记

day2

总结：今天学习了线性回归、梯度下降以及梯度下降在线性回归算法中的应用等内容。

线性回归算法用来解决有监督问题中的回归问题

【算法思想】：用历史经验（x[样本特征],y[样本结果]）来学习一个假设函数h，从而能够在对新样本中的x进行预测得到结果y。

用历史数据中的y与假设函数的结果h(x)进行对比，得到代价函数。

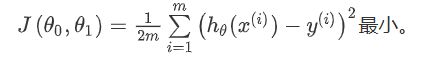
【假设函数的目标】是不断修改参数theta最终使代价函数达到最小值，即使假设函数的结果与真实结果y无限接近。

梯度下降-【求代价函数最小值】

【算法思想】:择一个参数的组合计算代价函数，然后我们寻找下一个能让代价函数值下降最多(求导，延切线的方向梯度下降最快)的参数组合。
注意：（1）梯度下降算法中的参数theta1,theta2…需要同步更新。
（2）Alpha 太大可能会越过最低点，无法收敛；alpha太小可能会收敛很慢。当接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度。
（3）梯度下降可能会陷入局部最优（偏导=0，theta不会再变），

【线性回归中的梯度下降算法】

day3

总结：【线性代数回顾】主要回顾了矩阵和向量的部分知识，其中包括矩阵、向量的定义，矩阵的加减运算、矩阵乘以向量，矩阵乘法的运算 和性质，以及矩阵的逆和转置的运算等内容

day4

总结：机器学习第二周任务主要包括多变量线性回归算法和octave教程的学习

多变量线性回归

与day2的线性回归算法比较，多元线性回归算法的不同之处就是样本的特征从一维变成了多维度。X表示为(x1,x2,…,xn)。多变量线性回归算法的代价函数表示为：

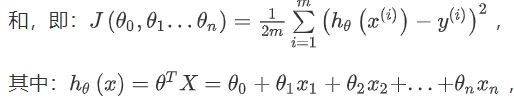
其对应的梯度下降算法为：

梯度下降算法实践注意事项

1、多变量线性回归算法的梯度计算过程中需要保证所有特征都有相近的尺度，这样能够帮助梯度下降算法更快的收敛。
解决方法：用【特征缩放】的方法将特征的尺度都缩放到-1~1之间，（xi=(xi-ui)/si,其中ui表示均值，si为方差。
2、【学习率】在day2学习中我们了解到，梯度下降算法的每次迭代受到学习率的影响，如果学习率过小，则达到收敛所需的迭代次数会非常高；如果学习率过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
解决方法：尝试alpha取值为：0.01，0.03，0.1，0.3，1，3，10
3、假设函数中的线性关系可能无法对模型进行很好的拟合，所有需要采用【多项式回归模型】创建假设函数。（采用多项式回归模型，在梯度下降算法前特征缩放是非常有必要的）
4、梯度下降算法是比较通用的解决回归或分类模型中参数的方法。针对某些线性回归问题，也可以用【正规方程方法】计算模型中的参数theta。
【注意】对于那些不可逆的矩阵（特征之间不独立），正规方程方法是不能用的。

梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率alpha	不需要
需要多次迭代	一次运算得出
当特征数量n大时也能较好适用	需要计算(x’x)-1 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为o(n^3)，通常来说当小于10000 时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数的替代方法。具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。

day5

【总结】本节学习逻辑回归的定义&假设函数&梯度下降算法,以及正则话在线性回归\逻辑回归中的应用.

与线性回归不同的是，线性回归预测的y是连续值，即回归问题。而逻辑回归预测y是离散值，即分类问题。
逻辑回归-假设函数

判定边界：将不同类型的数据进行区分的边界线
【代价函数】模型误差的平方和，代价函数是一个非凸函数(non-convexfunction),意味着代价函数有许多局部最小值，影响梯度下降算法找到全局最小值。


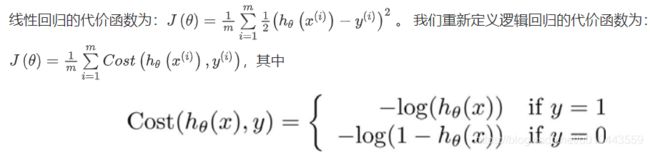
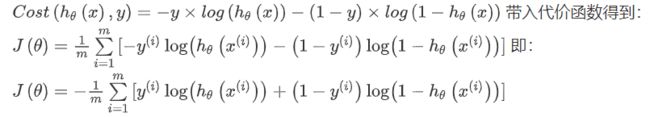
为了拟合参数我们需要找到使代价函数达到最小值的参数theta。
最小化代价函数方法-【梯度下降(gradient descent)】

三个步骤：计算J、计算i=0,n的J对theta_i的偏导、同步更新theta。
注意：
a、theta需要同步更新
b、用特征缩放的方法提到线性回归梯度下降算法的收敛速度，这样的方法同样适用于逻辑回归。

多分类问题

多分类问题是二分类问题的延申，可以用二分类的思想解决多分类的问题：首先我们将多个类中的一个类标记为正向类（y=1），然后将其他所有类都标记为负向类，这个模型记作$h{1}_{t}heta(x)$。接着，类似地第我们选择另一个类标记为正向类（y=2），再将其它类都标记为负向类，将这个模型记作h2 ,依此类推。 最后我们得到一系列的模型简记为：
最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

正则化(Regularization)

正则化(regularization)的技术，它可以改善或者减少过度拟合问题。
【欠拟合】：模型不能很好的适应训练集
【过拟合】：模型过于强调拟合原始数据，而丢失了算法的本质。若给出一个新的值使之预测，它将表现的很差。
解决过拟合方法：
a、丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
b、正则化。 保留所有的特征，但是减少参数的大小（magnitude）。

使模型的高阶多项式的系数尽可能的小，即减少theta_3,theta_4的值。（在代价函数J中给theta_3、theta_4前面的系数给个大一点的值，想要使J最小，就必须让theta_3、theta_4尽可能的小）

lamda为正则化参数。注意：lamda太小，达不到正则化的目的；lamda太大，则会使theta(除theta_0)都会趋近于0，使模型欠拟合.

正则化的线性回归

正则化的逻辑回归

代价函数

day6

【总结】今天学习了神经网络的前向传播算法
线性回归 和 逻辑回归的缺点 ：特征太多，计算的负荷比较大。
神经网络模型建立在很多神经元之上，每一个神经元又是一个个学习模型。这些神经元（也叫激活单元，activation unit）采纳一些特征作为输出，并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例，在神经网络中，参数又可被成为权重（weight）。

day7

【总结】今天学习神经网路的代价函数、反向传播算法等知识点
假设有m个样本


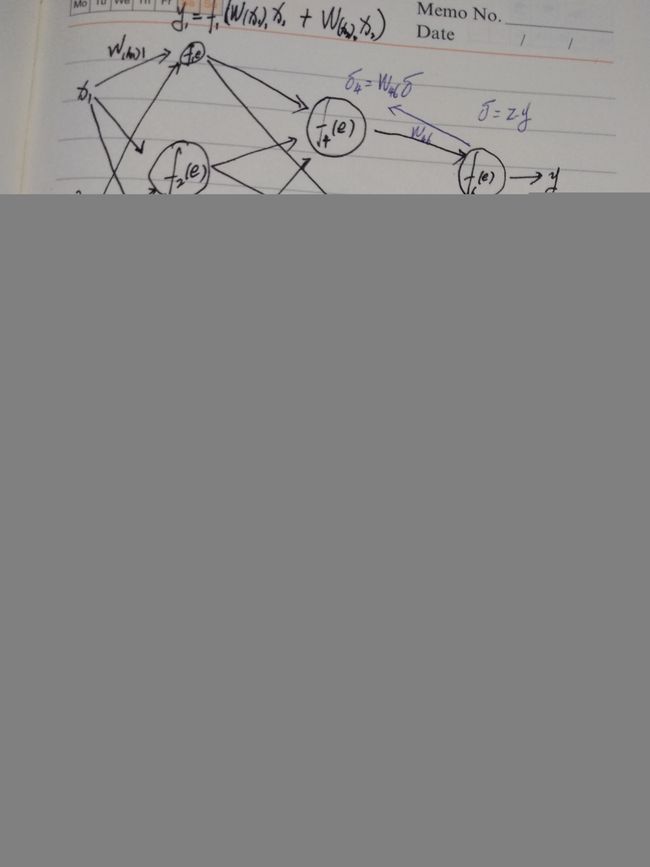
首先用正向传播算法计算出每一层的激活单元，利用训练集的结果与神经网络的结果求出最后一层的误差，然后利用该误差运用反响传播算法计算出直至第二层的所有误差。
反响传播的步骤：
1、用正向传播算法计算出每个神经元的输出，直到最后一层。
2、利用最后一层的输出与标签值进行比较，计算出误差delta
循环：用第i层的误差$delt{a}_i$ 和 神经元之间的权重 $w_{(}i,j)$计算出第i-1 层 神经元的误差$delt{a}_i-1$
3、根据误差反向传播误差，获得每一个神经元的误差值，再根据误差值和e的倒数来【更新权重】，达到了对整个网络的修正。

conference

笔记目录：http://www.ai-start.com/ml2014/