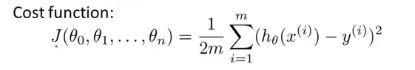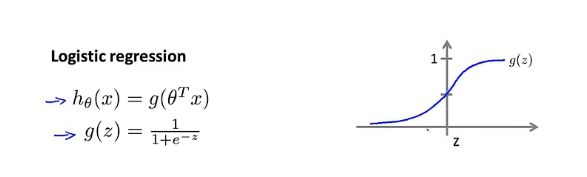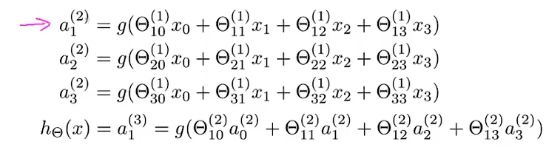机器学习浅尝一下

在b站上学习吴恩达老师的机器学习有感，插个眼大致做个初步笔记并不断补充，看别人的笔记不如自己做笔记印象来得深刻，建议大家都去听一遍。
哔哩哔哩传送门：https://www.bilibili.com/video/BV164411b7dx?p=1

机器学习：使计算机具有自主学习能力，从经验E中进行学习，在提高性能度量P中完成任务T。

1. 常用的的机器学习算法
   监督学习：教计算机做某事
   无监督学习：让计算机自己学习
   半监督学习：（学习样本中部分记录有结果标记）
2. 机器学习三大基本模型
   分类模型、回归模型（RM）、聚类模型
3. 支持向量机算法：允许计算机处理无穷多的特征
   一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器。

一、First Day

1. 监督学习

给算法一个数据集，其中包含了正确答案y

1.1 分类算法

通过对训练集的学习将属性映射到目标上，预测离散值0、1或两个以上的离散输出。

分类算法常用的评估指标：
精确率：预测结果与实际结果的比例
召回率：预测结果中某类结果的正确覆盖率
F1-Score：统计量，综合评估分类模型的指标，取值0~1之间，越大模型可用度越高

分类算法：KNN算法、决策树
分类模型：logistic回归模型（可包含多个非线性项）

1.2 回归算法

设法预测一个连续值的输出 ，让一条直线拟合数据，可用二次函数或二阶多项式

回归算法：KNN算法
回归模型：线性模型(Linear Model)、多项式模型(Polynomial Model)
（训练集特征次数越高，拟合所涵盖的范围越广，预测也越准确，但过于复杂的模型可能产生过拟合问题）

损失函数loss：评价模型所产生的预测结果的一个函数，根据损失函数的反馈值调整参数

2. 无监督学习

从无标记的训练数据中推断结论

2.1 聚类算法

自动按照的到的类型将个体分成不同的簇，例如谷歌新闻的标签分簇行为，聚类分析所使用的方法不同，往往会得出不同的结论。

聚类算法：K-Means

2.2 鸡尾酒会算法

帮忙找出数据的类型结构，分离被混合到一起的音频源

3. 模型描述

m：表示训练样本的数量
x：表示输入变量/特征
y：表示预测输出的目标变量
(x,y)：一个训练样本
(x^(i) ,y^(i))：特定第i个训练样本
h：假设函数，一个引导从x得到y的函数

4. 线性回归：一元线性回归（单变量线性回归）

假设函数h(x)=a+bx如何决定参数a、b，将最有可能的直线与我们的数据相拟合？
即要解决关于a、b的最小化问题，减少假设的输出值与真实值之间的差平方。

定义一个代价函数（平均误差函数、平方误差代价函数）
=样本数的一半 * (输出值与真实值之间的差平方之和）
要找到使代价函数为最小值的参数是多少

5. 梯度下降算法

初始化参数，使代价函数不断变小，直至找到最小值或局部最优值

学习速率代表着改变参数引起变化的步伐，太小的话梯度下降过慢，太大的话可能越过最优点无法收敛甚至发散。

假如初始化等于局部最优点，导数项会等于0，梯度下降法不会改变什么。

当我们接近局部最优点时，梯度下降法会自动采取更小的幅度。

6. 将梯度下降法应用到最小化平方差代价函数（Batch梯度下降算法）

二、Second Day

1. 多功能/多变量 Multiple features（variable）

x1	x2	x3	x4	y
1	2	3	4	5
1	2	1	4	7
1	2	2	7	4

特征量 n = 4
样本数量 m = 3
第i个训练样本的输入特征值 x^(1) = [1 2 3 4]^T ：四维的特征向量（一列而不是一行）
第i个训练样本的输出值 y^(1) = [5]
h(x) = a^(T) · x = a0x0+a1x1+…+anxn

2. 多元梯度下降法

①如何设定假设的参数？
②使用多元梯度下降法处理多元线性回归

代价函数

梯度下降（不断更新参数）

3. 多元梯度下降法——特征缩放法

并不需要太精准，只是为了让梯度下降，收敛所需的迭代少一点，运行的快一点

3.1 特征值

不同特征的取值在相近的范围内，能使梯度下降法能快收敛

一般将特征值的取值约束到-1到+1的范围内，或者附近范围足够接近

3.2 均值归一化

x属于（0,2000）
x1 = (size - 范围均值）/（范围差值）

4. 多元梯度下降法——学习率

适用于回归模型，只要学习率足够小，每次迭代之后的代价函数J(θ)都会下降。

4.1 确保梯度下降正常工作

梯度下降法->找到θ值，并希望能够最小化代价函数J(θ)

①通过迭代次数-代价函数值图像，得到J(θ)逐步下降的趋势，判断梯度下降法是否已经收敛

②自动收敛测试（通过另外一种算法）

4.2 如何选择学习率

迭代次数-J(θ)图像	常见原因	学习率修正
逐步上升	α值过大，梯度调整越过最小值	降低α值
下降过慢	α值过小，收敛过慢	提高α值

从1、0.1、0.001、（0.0005）、0.0001逐步以十分之一递减，找到较好的学习率

5. 特征和多项式回归

5.1 可供选择的特征

①原有特征
②利用原有特征创造新的特征

5.2 如何得到不同的学习算法

使用其他算法原因：二次模型能很好拟合，但是二次函数最终会下降。

多项式回归模型：可以使用多元线性回归的方法，对算法进行简单修改来实现（梯度下降法要注意好特征的缩放）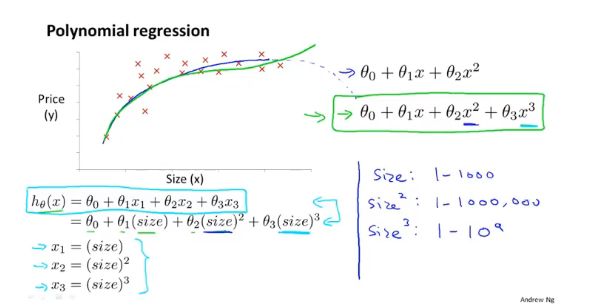

6. 正规方程

区别于迭代方法的直接解法，对于某些线性回归方程，提供更好的方法一次性求解参数θ的最优值（不需要特征缩放），但是不适合更复杂的学习算法。

6.1 等价使得J(θ)最小化的θ值

加一列x0进行矩阵设计，X = m*（n+1）维矩阵、y = m维向量
m是训练样本的数量、n是特征变量数


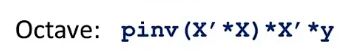
得到使得代价函数最小化的θ

6.2 何时使用梯度下降法、正规方程法

方法选择	优点	缺点	适合特征数
梯度下降法	特征变量大量也可以运行好	需要测试学习速率α、多次迭代	n=10000
正规方程法	不需要选择α值，易实现	特征变量多计算θ会慢	n=1000

6.3 不可逆性解决方法

在octave中使用pinv即使矩阵不可逆也能算出来违逆函数，但inv就不一定。
①查看数据中是否有些多余的特征并删掉 ；互为线性的特征删除其中一个；没有多余但是过多，在影响不大下删除一些特征；或考虑正规化方法。

7. 向量化的方法

利用octave高度优化的数值线性代数算法来计算θ和x两个向量的内积，利用向量化的方法得到一个更为高效的线性回归算法。

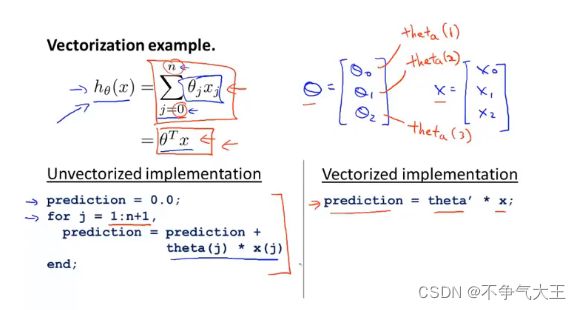
8. Logistic回归算法

预测值y为离散值的情况

二分类/二元分类问题 ：0（负类）、 1（正类）
多分类：0、1、2、3

8.1 为何开发Logistic分类算法

1、把线性回归方程应用到数据集
2、用直线对数据进行拟合
3、设置一个阈值，大于阈值即等于1、小于则等于0

把线性回归应用于分类问题通常不是一个好的选择，易受干扰，输出值可能会大于1或小于0；改用Logistic回归算法可以让输出的预测值一直介于0和1之间。

8.2 假设陈述

Logistic回归不是回归算法，而是分类算法

目标：希望分类器的输出值在0和1之间

Logistic回归中假设函数的表示方法：利用Sigmoid function（Logistic function）对方程做出改变，让g(z)在0和1之间，使得h(θ)也落在0和1之间。

假设将特征值x输入模型中，输出的h(θ)为y=1的概率。

8.3 决策界限

如果h(θ)=g(z) ≥ 0.5，即z ≥ 0，输出y=1
如果h(θ)=g(z)＜0.5，即z＜0，输出y=0
z为设置的公式（低阶/高阶多项式）-> 更复杂的决策边界

红线即为决策边界（假设函数的一个属性，决定于参数的设置）

8.4 代价函数

学习拟合logistic回归模型的参数θ -> 用来拟合参数的优化目标称为代价函数

寻找一个为凸函数的代价函数，并且用于梯度下降法找到全局最优

8.5 简化代价函数与梯度下降

利用梯度下降法拟合出logistic回归的参数

8.6 高级优化

优化代价函数的不同方法
后三种算法
优点：不需要手动选择学习率α，收敛速度远快于梯度下降
缺点：复杂，直接调用相关的库即可

8.7 多元分类：一对多分类算法

使用逻辑回归解决多类别分类问题 y=1、2、3…离散值

有三个类的数据集：转化为三个独立的二元分类问题

①将第1、2类分为一类 =》识别y=3的概率
②训练第一个标准的逻辑回归分类器，得到判定边界
③将第1、3类分为一类 =》识别y=2的概率
④训练第二个标准的逻辑回归分类器，得到判定边界
⑤将第2、3类分为一类 =》识别y=1的概率
⑥训练第三个标准的逻辑回归分类器，得到判定边界

9. 过拟合问题

过拟合导致表现欠佳 <- 正则化技术改善

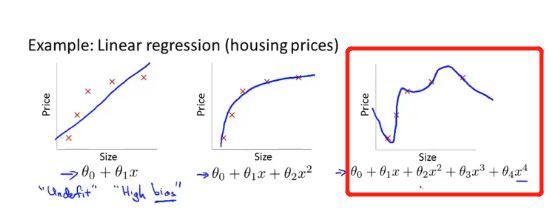
过度拟合：通过了所有的点，但曲线扭曲无法预测新样本，在变量过多的时候会出现。
泛化能力：一个假设模型应用到新样本（没有出现在数据集）的能力

9.1 利用工具来识别过拟合和欠拟合情况

绘制假设模型曲线

拟合程度	原因	解决方法
过度拟合	特征量过多、训练数据非常少	①尽量减少选取变量的数量 （模型选择算法）②保留所有特征但减少量级或参数大小（正则化）
欠拟合	特征量过少、模型复杂度过低	①增加新特征 ②添加多项式特征 ③减少正则化参数 ④使用非线性模型

9.2 正则化

优化目标：最小化均方误差代价函数，加入惩罚项让高阶项的参数尽可能小，得到更简单的函数，近似于二次函数（参数越小，线段越平滑）

如果特征值过多，不知道该缩小哪些项，就在末尾加入正则化项，缩小每一个参数，但正则化参数λ不能设置太大，会导致对每一项的惩罚力度太大都趋向于0。

可将正规方程和梯度下降两种算法推广到正则化线性回归进行。

三、Third Day 被称为神经网络的机器学习算法

样本中含有大量特征值，logistic回归并不适用，神经网络能很好地解决不同的机器学习问题。

1. 神经网络表示假设或模型

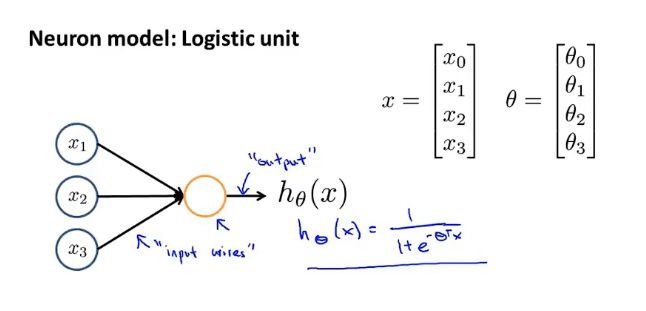
可以在前面加上x0=1 称为偏置单元或偏置神经元
通常会说这是一个带有sigmoid或者logistic激活函数的人工神经元

激活函数：通常指代非线性函数g(z)
模型权重weights：模型参数θ

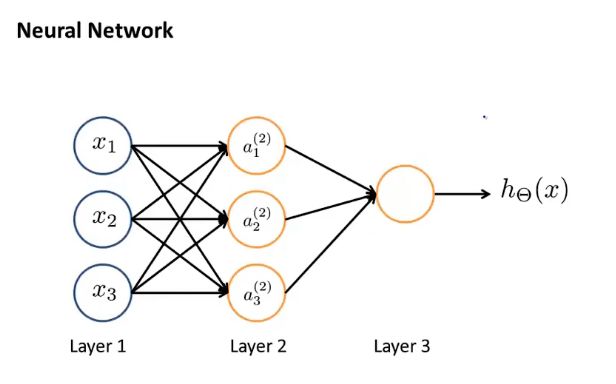
神经网络其实就是一组神经元连接在一起的集合

第一层（输入层）：输入特征值x1 x2 x3
第二层（隐藏层）：中间有三个神经元a1 a2 a3（可以不止一个隐藏层）
第三层（输出层）：第三个节点，这一层的神经元输出假设的最终计算结果

神经网络究竟在做什么？

激活项：由一个具体神经元计算并输出的值

三个隐藏单元和输出层：通过激活函数计算相应的激活值

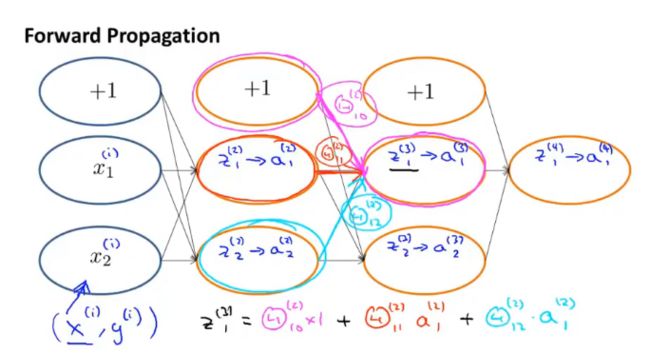
2. 将神经网络的计算向量化

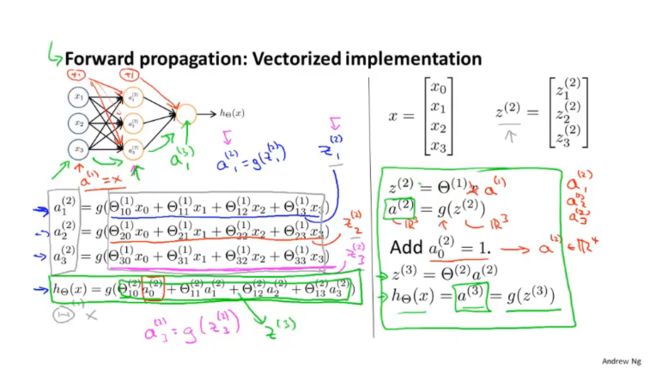
前向传播：通过上一层的i,j,k等结点以及对应的连接权值进行加权和运算，最终结果再加上一个偏置项，再通过一个非线性函数（即激活函数），如Relu、sigmoid等函数，得到的结果就是本层结点的输出。

神经网络与逻辑回归相似，但区别在于神经网络不是使用原有特征值x来训练逻辑回归，而是使用隐藏层得到的a作为新特征值。

神经网络的架构：神经网络中神经元的连接方式

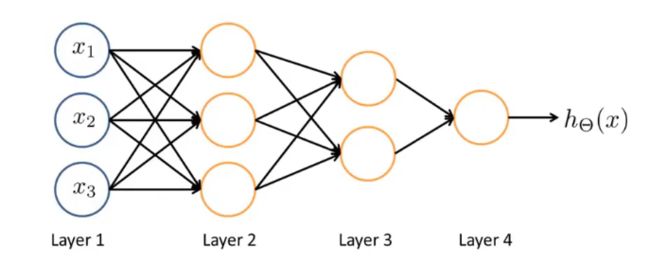
非线性假设函数
第一层：将输入层的激活项通过前向传播到后面的隐藏层，直到输出层
第二层：隐藏层，将输入层的原始特征项作为输入，计算出更为复杂的特征
第三层：隐藏层，将第二层训练出的特征项作为输入，计算出更为复杂的特征
第四层：逻辑回归器最后一层输出层

3. 神经网络中单个神经元如何被用来计算

4. 利用神经网络得到非线性决策边界

5. 利用神经网络解决多类别分类问题

数字识别：0-9的多类别分类问题

要在神经网络中实现多类别分类，采用的方法本质上是一对多方法的扩展

四个逻辑回归分类器，每一个都将识别图片中的物体是否为四种类别中的一种

6. 代价函数

在给定训练集时，为神经网络拟合参数

7. 反向传播算法

让代价函数最小化的算法，比线性回归算法和逻辑回归算法要复杂

前向传播算法

反向传播算法

计算代价函数的倒数

8. 梯度检验

实现反向传播或者类似梯度下降算法时，保证前向传播或反向传播的正确

9. 随机初始化

①权重全部设置为0（不可取）
②权重随机初始化为接近0的范围，再进行反向传播和梯度检验、梯度下降或者其他高级优化算法来最小化代价函数J

10. 神经网络实现过程

10.1 选择架构

在训练一个神经网络时，先选择一个神经网络架构
1、定义输入单元的数量（特征集x的维度）
2、输出层的单元数目（多类别分类中所要区分的类别个数）
3、隐藏层单元个数和隐藏层层数（默认单个，或者多层拥有相同单元个数）

10.2 训练神经网络需要实现步骤

1、构建一个神经网络架构，随机初始化权重
2、执行前向传播算法
3、计算出代价函数J(θ)
4、执行反向传播算法求出偏导数项
5、使用梯度检查比较计算得到的偏导数项，确保两种方法得到基本接近的两个值
6、使用一个最优化算法（梯度下降算法、LBFGS算法、共轭梯度法等）

四、Forth Day 机器学习诊断法

1. 评价算法学习得到的假设

在模型中选择好参数来使训练误差最小化，训练误差越小不一定越好，可能会过拟合，这时泛化能力就不见的好了。

将数据随机分为训练集train、测试集test（7:3）

线性回归问题、逻辑回归问题：
1、训练数据：对训练集进行学习得到参数θ（最小化训练误差J(θ)）
2、将参数θ用来计算测试误差J_test（假设函数的平方误差）

2. 训练集train、验证集val、测试集test

存在过拟合原因：训练集误差不能用来判断该假设对新样本的拟合好坏

2.1 如何选择一个模型

加上参数d、取每个n次函数和相应的参数θ，得出测试误差J_test进行比较，但仍不能得到很好地泛化能力

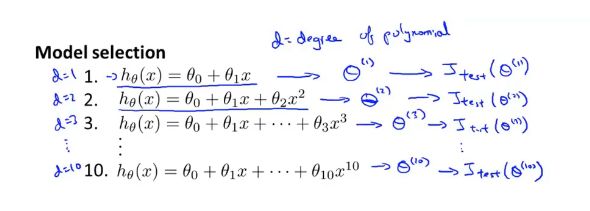
2.2 如何合理评估一个假设

将数据集分为训练集train、交叉验证集val、测试集test（6：2：2）

定义训练误差、验证误差、测试误差

用验证集来选择模型，而不是原来的测试集

1、选取第一个模型，然后最小化代价函数，得到对应的参数向量θ
2、对后续模型重复步骤
3、用交叉验证集来检验效果
4、选择最小的验证集误差，得出最合适的参数d，即这个多项式次数

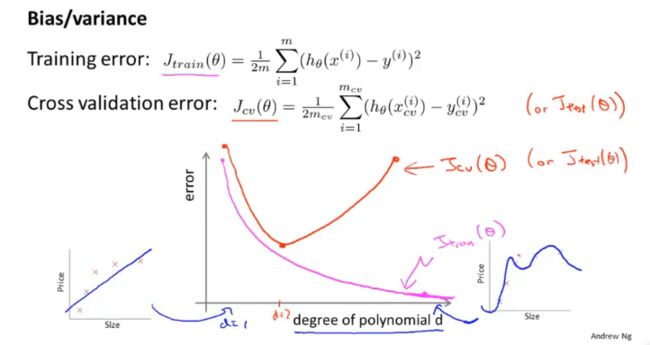
3. 诊断偏差与方差

欠拟合、过拟合 -> 偏差或方差较大

随着方程复杂度增加，训练集误差和交叉验证集误差不同

欠拟合：train-error和val-error都很大，多项式次数过小，是高偏差问题；
过拟合：train-error和val-error具有较大高度差，多项式次数过大，是高方差问题；

3.1 正则化如何影响偏差和方差

加入正则化项让参数θ尽量小，可以有效防止过拟合

正则参数过大，容易欠拟合（产生高偏差）；过小容易，过拟合（产生高方差）

如何选择正则化参数λ？
1、考虑不使用正则化，选取一系列想要尝试的λ值0、0.01、0.02…
2、在每个模型中最小化代价函数J(θ)，得到对应的参数向量θ，用交叉验证集进行评价
3、选取交叉验证集误差最小的模型
4、用交叉验证集拟合参数后，用测试集进行评价

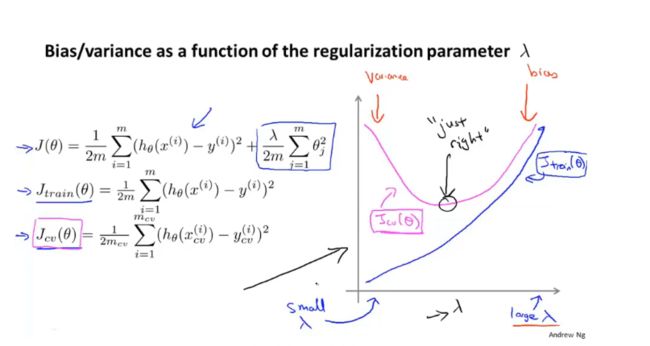
4. 学习曲线

检验运行是否一切正常、改进算法

用正则化去修正更便捷一点

5. 执行的优先级（垃圾邮件分类器）

如何通过监督学习构造一个分类器来区分垃圾邮件和非垃圾邮件？

5.1 构造邮件的特征向量x和分类标签y

要想使用监督学习，思考如何构造邮件的特征向量x和分类标签y，有了x和y才能构造分类器，例如使用逻辑回归等方法

选择邮件的特征向量的方法：提出一个可能含100个单词的列表进行区分（实际上选取出现频率最多的n个单词作为特征向量）

5.2 思考用更复杂的特征变量\算法提高学习效果

五、Fifth Day

1.误差分析

除了绘制学习曲线外，误差分析也可以帮助我们系统地作出选择，通过数值来评估算法的效果，在交叉验证集上做误差分析，而不是测试集。

当需要对目标进行机器学习时，最好先粗暴的做出一个简单的模型来实现初始算法，尽管他的效果可能不太好，但是通过后续误差分析等不断做出优化，可以更好的实现目标。

2. 不对称性的误差评估

如何使用一个合适的误差度量值？

偏斜类：在样本数据中y=0和y=1的比值趋于极端情况，某一类数据很少

对于偏斜类使用分类精确度，并不能很好地衡量算法，可能会出现预测y=0但是提高了评估数值的情况。需要一个不同的误差度量值/评估度量值，其中一种叫做查准率和召回率。

需要加入查准率和召回率对模型进行好坏评价！
查准率precision：对于预测出y=1的数据中，有多大比例的x是真正y=1的。真阳性/（真阳性+假阳性）查准率越高越好
召回率recall：对于真正y=1的数据中，有多大比例的x能被预测出来y=1。真阳性/（真阳性+假阴性）召回率越高越好

3.精准度和召回率的权衡

高查准率模型（低召回率）：对于预测癌症患者，将决策界限从0.5提高到0.7能够更加准确的预测患癌，该模型的precision会提高，但是会有较低的recall。
高召回率模型（低查准率）：对于预测癌症患者，将决策界限从0.5降低到0.3避免遗漏癌症患者，该模型的recalln会提高，但是会有较低的precision。

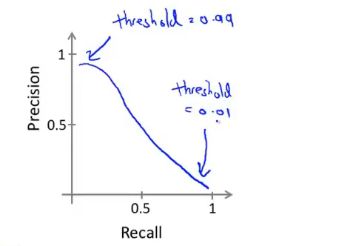
有没有办法自动选取临界值，或者在多个算法中如何比较查准率和召回率？

1、计算查准率和召回率的平均值（不太可行）
2、计算F值（有多种）

4. 机器学习数据

随着训练数据的增加，在基于特征值含有较为完善的内容下，算法的性能可能会越来越好。

5. 优化目标

如何优化目标 -> 优化相应的公式方程（代价函数等）

支持向量机监督学习算法：支持向量机SVM，与logistic回归和神经网络相比，在学习复杂的非线性方程时，能够提供一种更为清晰的和更加强大的方式。

支持向量机并不会输出概率，而是通过优化代价函数得到一个参数θ，通过假设函数直接进行预测。

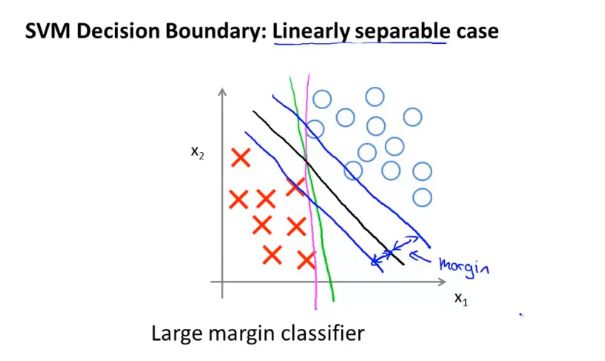
6. 支持向量机（大间距分类器）

SVM具有更稳健的决策边界，能更好地分开正样本和负样本，拥有更大的距离（间距），和训练样本的最小距离要大一点（支持向量机的间距），这使得支持向量机具有鲁棒性，因为它在分离数据时会尽量用大的间距去分离。

鲁棒性：指系统在受到扰动或者不确定的情况下，仍然可以维持某些性能的特性。

7. 核函数

改造支持向量机算法来构造复杂的非线性分类器

弹幕大佬：核函数把损失函数中的θ和x内积中的x改为f(x)，加了一层神经元，是一种优化SVM的方法。

8. 使用SVM

调用软件库去实现liblinear、libsvm

9. 无监督学习

插个眼下次再学