【Pytorch(五)】基于 PyTorch 构建卷积神经网络 CNN
基于 PyTorch 构建卷积神经网络 CNN
文章目录
- 基于 PyTorch 构建卷积神经网络 CNN
-
- 0. 概述
- 1. 导入 PyTorch 及其他相关库
- 2. 准备数据集 (Data Preparation)
- 3. 定义一个神经网络
- 4. 训练神经网络
0. 概述
在前面两项实验内容中,我们已经学习了 PyTorch 的基本数据类型 tensor 及其相关操作,并练习了如何通过 PyTorch 读入并处理数据集。下面,我们就正式开始学习如何基于 PyTorch 搭建一个神经网络,并在 MNIST 数据集上进行训练和测试。
总体来讲,我们在这部分实验中要进行的操作包括以下几点:
1) 读取和处理数据集
2) 定义一个包含可训练参数的神经网络
3) 从数据集中取出一个批次 (batch) 的样本传递给神经网络
4) 通过神经网络处理输入样本
5) 计算损失 (loss)
6) 反向传播计算偏导
7) 更新网络的参数 (一个简单的更新方法:weight = weight - learning_rate *gradient)
8) 重复 3) 到 7) 步,不断调整网络参数
1. 导入 PyTorch 及其他相关库
import torch
import torchvision
import numpy as np
查看 PyTorch 版本,是否可以使用 GPU,及 CUDA 的版本。
print(torch.__version__)
print(torch.cuda.is_available())
print(torch.version.cuda)
1.7.1+cu110
True
11.0
2. 准备数据集 (Data Preparation)
batch_size = 100 # 设置训练集和测试集的 batch size,即每批次将参与运算的样本数
train_set = torchvision.datasets.MNIST('./dataset_mnist', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,)
)
])
)
##################### please finish the code ########################
# 请把之前在“1_mnist_dataset_import.ipynb”中写的 test_set 代码复制在这里
# test_set = XXX
test_set = torchvision.datasets.MNIST('./dataset_mnist', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,)
)
])
)
################################ end ################################
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size, shuffle=True)
3. 定义一个神经网络
为了构建神经网络,我们将使用 torch.nn 包,它是 PyTorch 的神经网络库。我们通常会将 torch.nn 包直接导入并命名为 nn。
import torch.nn as nn
PyTorch 的神经网络库包含了构建神经网络所需的所有典型组件。我们构建一个神经网络使用的最主要组件是层,所以 PyTorch 的神经网络库包含了帮助我们构造层的类。在神经网络包里有一类被称为“模块” (nn.Module) 的特殊类,它是所有神经网络模块的母类。PyTorch 中所有的神经网络层均继承了 nn.Module。
神经网络中的每一层都包含两个主要组成部分,第一是该层参数的集合 (weights and biases),第二是该层进行的变换 (transformation)。其中,进行的变换主要指前向传播过程,每一个 PyTorch nn.Module 都有一个 forward() 函数来定义其前向传播。因此,当我们实现一个自定义的神经网络 (nn.Module 子类) 时,也需要编写其 forward() 函数。值得注意的是,得益于 PyTorch 的自动求导功能,我们并不需要像“实验一”中一样自己编写反向传播的 backward() 函数,PyTorch 会自动帮我们完成。(关于这一点,我们会在之后的实验中详细为大家介绍。)
总结起来,在 PyTorch 中定义神经网络包括如下几个步骤:
-
基于 nn.Module 创建一个类 (extend the nn.Module base class)
-
在类构造函数中,将网络的层定义为类属性 (define layers as class attributes)
-
定义网络的前向传播 (implement the forward() method)
下面,我们就可以创建一个类来表示一个简单的神经网络。
class Network0(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.layer = None
def forward(self, t):
t = self.layer(t)
return t
在这个例子中,我们扩展了 nn.Module 基类。它在构造函数中有一个虚拟层 (self.layer),并在 forward() 函数中实现了一个虚拟的前向传播过程。forward() 接收来自神经网络输入端的张量 t,对其进行张量变换 (transformation),并将变换后的结果返回。
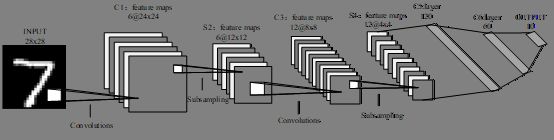
现在,让我们用一些真正的层来替代这个虚拟层,这些层将由PyTorch 神经网络库提供。我们将建立一个卷积神经网络,包含两个卷积层和三个全连接层。其中,卷积层我们将用 torch.nn 的内建层类 nn.Conv2d 来实现,全连接层将用 nn.Linear 来实现。
nn.Conv2d 可见 PyTorch 官网: https://pytorch.org/docs/master/generated/torch.nn.Conv2d.html#torch.nn.Conv2d
nn.Linear 可见 PyTorch 官网: https://pytorch.org/docs/master/generated/torch.nn.Linear.html#torch.nn.Linear
假设我们将使用 MNIST 数据集,每张图片为一个 28*28 的灰度图。在即将定义的神经网络中,每个卷积层之后我们都会进行池化操作 (pooling),池化的 kernel 大小和 stride 均取 2(即每次将对 2*2 的元素进行 max pooling)。 池化层由于不包含可训练的参数,因此不作为 Network1 的类属性(class attribute),而是会在之后写入 forward() 函数里。
class Network1(nn.Module):
def __init__(self):
super(Network1, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, # 输入通道数
out_channels=6, # 输出通道数
kernel_size=5) # kernel 大小 (对应四维权重张量的 dim2/dim3)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
##################### please finish the code ########################
# self.fc1 = nn.Linear(in_features=XXX, # 输入激活向量的长度
# out_features=120) # 输出激活向量的长度
self.fc1 = nn.Linear(in_features=192, out_features=120)
################################ end ################################
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
# we will implement the forward path later
return t
代码解释:这里是第一个全连接层,它的输入应该是特征张量经过两层卷积,两层池化的张量拉平后的特征数量。由上图可知全连接的前一层是输出一个12x4x4的三维张量,拉平计算出特征个数为192。因此,此空应该填写192。
查看定义好的网络结构
network = Network1()
print(network)
Network1(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=192, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=60, bias=True)
(out): Linear(in_features=60, out_features=10, bias=True)
)
查看卷积层及其参数
Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
print(network.conv1.weight) # check the weights of conv1
Parameter containing:
tensor([[[[-0.0594, 0.0425, 0.0493, -0.1925, -0.0007],
[-0.0205, -0.0643, -0.1029, -0.1133, -0.0529],
[ 0.1931, 0.0444, 0.0907, 0.0706, 0.1145],
[-0.0771, 0.0453, -0.1527, -0.1388, 0.0241],
[ 0.1286, 0.1522, -0.0919, -0.0032, 0.0155]]],
[[[-0.1433, 0.0960, 0.0374, 0.0428, 0.1102],
[ 0.0486, 0.1576, -0.1700, -0.1058, 0.0916],
[-0.1973, 0.0576, -0.1478, 0.0998, -0.1304],
[ 0.1752, 0.0953, 0.1984, 0.0957, -0.1613],
[ 0.0834, -0.1608, 0.1086, 0.1325, 0.0568]]],
[[[-0.0506, 0.1058, 0.1460, -0.0202, -0.1679],
[ 0.1060, -0.1501, 0.1612, 0.1004, 0.0375],
[ 0.1802, -0.0040, 0.0755, -0.0585, -0.0204],
[ 0.0536, -0.0284, -0.0040, -0.1625, 0.1793],
[-0.0878, -0.0131, -0.0022, 0.1125, 0.1211]]],
[[[ 0.1233, -0.1757, -0.0831, 0.1451, 0.0897],
[ 0.1899, 0.0472, 0.1208, -0.1191, 0.0794],
[-0.0523, 0.0451, 0.0682, 0.1365, -0.0604],
[-0.1362, 0.1054, -0.1874, -0.0777, 0.1690],
[ 0.0094, 0.0829, -0.1800, -0.1377, 0.0510]]],
[[[ 0.1025, -0.1373, -0.1825, 0.1499, -0.0550],
[ 0.0860, 0.0571, -0.0274, 0.0951, -0.1526],
[-0.1932, 0.1938, -0.1422, -0.1451, -0.0634],
[ 0.1754, -0.1755, 0.1224, 0.0838, -0.0414],
[-0.0223, -0.1874, -0.0100, 0.0086, 0.1742]]],
[[[-0.1008, -0.0192, 0.0793, -0.1070, 0.0990],
[ 0.0631, 0.0327, -0.0732, 0.0610, 0.0688],
[ 0.1564, 0.0463, 0.1076, 0.1192, -0.0745],
[ 0.0695, 0.0215, 0.1062, 0.0455, 0.0783],
[-0.0174, 0.0129, -0.1974, -0.1194, -0.1785]]]], requires_grad=True)
print(network.conv1.weight.shape) # check the shape of conv1's weight tensor
print(network.conv1.weight[0]) # check weigth[0]
print(network.conv1.weight[0].shape) # check the shape of weight[0]
torch.Size([6, 1, 5, 5])
tensor([[[ 0.1347, 0.1266, -0.1525, -0.0372, 0.0493],
[ 0.0575, 0.0078, -0.0345, -0.0093, 0.0675],
[ 0.1881, -0.1785, -0.0201, 0.0066, 0.0210],
[-0.1971, 0.1559, 0.1987, -0.0260, -0.0534],
[-0.0735, 0.0824, -0.1592, -0.1246, 0.0716]]],
grad_fn=)
torch.Size([1, 5, 5])
查看全连接层及其参数
# weight tensor for fc layers
print(network.fc1.weight.shape)
print(network.fc1.weight[0].shape)
torch.Size([120, 192])
torch.Size([192])
查看整个网络的参数
# 方式一
for name, param in network.named_parameters():
print(name, '\t\t', param.shape)
print("")
#方式二
for name in network.state_dict(): # state dictionary
print(name, '\t\t', network.state_dict()[name].shape)
# 查看 conv1 的参数
print(network.state_dict()["conv1.weight"].shape)
print(network.state_dict()["conv1.weight"])
conv1.weight torch.Size([6, 1, 5, 5])
conv1.bias torch.Size([6])
conv2.weight torch.Size([12, 6, 5, 5])
conv2.bias torch.Size([12])
fc1.weight torch.Size([120, 192])
fc1.bias torch.Size([120])
fc2.weight torch.Size([60, 120])
fc2.bias torch.Size([60])
out.weight torch.Size([10, 60])
out.bias torch.Size([10])
conv1.weight torch.Size([6, 1, 5, 5])
conv1.bias torch.Size([6])
conv2.weight torch.Size([12, 6, 5, 5])
conv2.bias torch.Size([12])
fc1.weight torch.Size([120, 192])
fc1.bias torch.Size([120])
fc2.weight torch.Size([60, 120])
fc2.bias torch.Size([60])
out.weight torch.Size([10, 60])
out.bias torch.Size([10])
torch.Size([6, 1, 5, 5])
tensor([[[[-1.5001e-01, -1.3848e-02, -1.0378e-01, 6.7523e-02, 1.6334e-01],
[ 1.2181e-01, -1.5125e-03, 7.3304e-02, 1.8515e-01, 1.4063e-01],
[ 1.3865e-01, 1.3580e-01, -9.3696e-02, 1.8193e-01, -1.7815e-01],
[ 1.6409e-01, 1.1340e-01, -1.6066e-01, 8.7652e-03, 5.5207e-02],
[ 1.9840e-01, -3.1835e-02, 1.4939e-01, 7.9950e-03, -1.6087e-01]]],
[[[-1.5691e-01, 9.4586e-02, -3.1107e-02, -2.6422e-03, -2.0982e-02],
[-2.8013e-03, 1.3842e-01, -1.6488e-01, 6.3527e-02, 2.2672e-03],
[-4.7753e-02, -7.8992e-02, 3.7517e-03, 1.1435e-01, -6.0690e-02],
[-1.0773e-02, 1.4323e-01, -1.9731e-01, -7.9947e-02, 1.9909e-01],
[ 9.9044e-02, -1.8865e-01, -2.4798e-02, 1.6735e-01, 6.9572e-02]]],
[[[-4.4329e-02, -1.2067e-01, 9.5155e-02, -1.7678e-01, 1.3103e-01],
[-6.4749e-02, 1.3068e-01, 1.4119e-01, -1.8535e-01, -9.6761e-02],
[ 3.4565e-02, -2.7310e-02, 4.6535e-02, 4.1834e-02, 1.8054e-01],
[ 8.9089e-03, -7.6159e-02, 1.6551e-01, 1.4622e-01, 1.3593e-01],
[ 1.9994e-01, 6.4953e-02, 4.9864e-02, 7.4876e-02, -2.2937e-02]]],
[[[ 6.9347e-02, -1.5495e-01, 1.9534e-02, 1.0272e-01, -7.0459e-02],
[-3.4613e-02, -3.3175e-02, -1.3626e-01, -1.6995e-01, 3.2141e-02],
[-8.4856e-02, -4.0157e-02, 1.4215e-01, 4.0197e-02, -2.8605e-02],
[ 1.0961e-01, 6.0601e-02, 3.8085e-02, 1.9794e-02, -9.8676e-02],
[-2.4603e-02, -1.2351e-02, -1.1427e-01, -1.2311e-01, -1.7150e-01]]],
[[[ 1.1733e-02, 1.6737e-01, -1.9645e-01, 8.0192e-03, 1.1080e-01],
[-8.4502e-02, 8.6131e-02, -2.9822e-02, -1.2681e-01, -1.7805e-01],
[-1.1166e-01, -1.8238e-02, -1.7278e-01, 9.2117e-02, 1.7788e-01],
[-8.6538e-02, -4.2994e-04, -1.4617e-01, 6.7663e-02, 2.5682e-02],
[ 2.5579e-02, 4.7913e-03, 1.4916e-01, -4.2923e-02, 1.7944e-01]]],
[[[-9.9185e-02, -1.5752e-01, 5.4561e-02, -3.1454e-02, -2.5488e-02],
[ 6.2888e-02, 4.3282e-02, -1.6043e-01, 1.6768e-01, -1.0158e-01],
[-1.8152e-01, -2.4528e-02, 2.0376e-02, -1.6032e-02, 3.6327e-02],
[ 1.3927e-01, -6.5995e-02, -1.2325e-01, 1.2444e-01, -7.8324e-02],
[ 1.8502e-01, 5.7690e-03, 1.3328e-04, -1.2427e-02, 1.0027e-01]]]])
网络的卷积层和全连接层定义好了。现在,让我们来实现 forward() 函数。
神经网络 forward() 函数的编写通常需要使用来自 nn.functional 的函数,这个包为我们提供了许多实现前向传播时需要的神经网络操作,例如激活函数 ReLU 和池化操作 Max Pooling。值得注意的是,虽然我们常称它们为“激活层”和“池化层”,但实际上它们都是在执行某种操作,并不包含可训练的参数。因此,它们在 PyTorch 中并没有被作为层来处理,也没有继承 nn.Module 基类,而是包含在 nn.functional 中。
import torch.nn.functional as F
class Network2(nn.Module):
def __init__(self):
super(Network2, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
##################### please finish the code ########################
# 请把之前 Network1 的 self.fc1 复制到这里:
# self.fc1 = nn.Linear(in_features=XXX, out_features=120)
self.fc1 = nn.Linear(in_features=192, out_features=120)
################################ end ################################
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
# conv1
t = self.conv1(t)
t = F.relu(t) # 这里我们用到了 nn.functional 包中的激活函数 relu
t = F.max_pool2d(t, kernel_size=2, stride=2) # 这里我们用到了 nn.functional 包中的池化函数 max_pool2d (max pooling)
# conv2
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# 特别注意:最后一个卷积层的输出在流入全连接层之前,要对激活值的维度进行变换,变换后的张量
# 是二维张量,其中 dim0 对应该批次中的不同样本,dim1 对应每个样本流向全连接层的输入激活向量。
# 请完成如下代码。
##################### please finish the code ########################
# dim0:一个批次的样本数
# dim1:每一个样本的输入激活向量长度
# t = t.reshape(XXX,XXX)
t = t.reshape(batch_size,192)
################################ end ################################
# fc1
t = self.fc1(t)
t = F.relu(t)
# fc2
t = self.fc2(t)
t = F.relu(t)
# output layer
t = self.out(t)
return t
在 PyTorch 中,当我们直接调用对象名称 conv1/conv2/fc1/fc2 并将输入 t 传递给它时,对应的 forward() 函数将被调用。因此,在上述代码中, 我们直接将输入 t 传递给了 conv1,而没有使用 t = self.conv1.forward(t)。
到这里,我们已经完成了神经网络的构建。下一步,我们将训练这个神经网络来处理手写字体识别任务。
# 关掉 PyTorch 的自动求导功能
print(torch.set_grad_enabled(False))
network = Network2()
# 我们取一批图片给 network
batch = next(iter(train_loader)) # DataLoader object: train_loader
images, labels = batch
print(images.shape) # rank-4 tensor
print(labels.shape)
output = network(images)
torch.Size([100, 1, 28, 28])
torch.Size([100])
# 查看 output 形状: rank-2 tensor ([batch_size, # of classes])
print(output.shape)
torch.Size([100, 10])
# F.softmax(t, dim=1)会为每个预测类返回一个概率值,这些概率值之和等于1。我们没有将这一步放在 Network2.forward()
# 中来做,是因为我们在训练网络将使用交叉熵损失函数 nn.CrossEntropyLoss,它会在其输入上隐式的执行一个 Softmax 操作。
output_prob = F.softmax(output, dim=1)
# 在之前的练习中我们已经知道,torch.max(t, dim=1) 函数会返回两个 tensor,第一个 tensor 是每行的最大值;第二个
# tensor是每行最大值的索引,反映了批处理中每个图像的预测标签。
scores, predict_class = torch.max(output_prob, dim=1)
print("scores: \n", scores)
print("predicted labels: \n", predict_class)
scores:
tensor([0.1240, 0.1199, 0.1262, 0.1252, 0.1247, 0.1213, 0.1296, 0.1226, 0.1271,
0.1217, 0.1226, 0.1253, 0.1202, 0.1286, 0.1241, 0.1248, 0.1245, 0.1258,
0.1230, 0.1252, 0.1227, 0.1256, 0.1250, 0.1207, 0.1233, 0.1180, 0.1245,
0.1245, 0.1244, 0.1216, 0.1282, 0.1243, 0.1320, 0.1215, 0.1244, 0.1263,
0.1251, 0.1256, 0.1172, 0.1225, 0.1256, 0.1213, 0.1224, 0.1219, 0.1236,
0.1253, 0.1225, 0.1266, 0.1221, 0.1298, 0.1266, 0.1256, 0.1251, 0.1237,
0.1288, 0.1238, 0.1185, 0.1279, 0.1283, 0.1253, 0.1260, 0.1200, 0.1241,
0.1216, 0.1265, 0.1229, 0.1270, 0.1255, 0.1196, 0.1261, 0.1208, 0.1221,
0.1241, 0.1235, 0.1229, 0.1221, 0.1222, 0.1263, 0.1254, 0.1228, 0.1262,
0.1271, 0.1204, 0.1238, 0.1286, 0.1256, 0.1240, 0.1260, 0.1281, 0.1191,
0.1251, 0.1268, 0.1225, 0.1233, 0.1227, 0.1239, 0.1163, 0.1257, 0.1299,
0.1228])
predicted labels:
tensor([3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3])
# 查看实际标签
print("actual labels: \n", labels)
actual labels:
tensor([2, 3, 3, 7, 8, 1, 1, 3, 4, 3, 1, 4, 1, 3, 9, 4, 9, 6, 5, 5, 7, 4, 4, 5,
8, 9, 6, 7, 6, 7, 0, 2, 1, 8, 5, 6, 9, 4, 9, 8, 8, 7, 0, 4, 5, 4, 5, 1,
5, 4, 8, 8, 5, 4, 5, 5, 0, 3, 7, 7, 4, 8, 1, 4, 5, 3, 2, 2, 1, 2, 4, 7,
1, 5, 5, 8, 1, 9, 6, 5, 7, 0, 7, 3, 6, 9, 8, 6, 6, 7, 4, 0, 6, 5, 4, 9,
5, 1, 2, 8])
# 计算这一批样本识别的“准确率”
correct_predictions = (predict_class == labels).sum().item() # 识别正确的次数
print("correct predictions: ", correct_predictions)
print("\"accuracy\": ", correct_predictions/len(labels)*100, "%")
correct predictions: 12
"accuracy": 12.0 %
把这一部分代码(从"network = Network2()"开始)多跑几次你会发现,每次 “scores”、“predict_class” 等都会发生变化,请思考这是为什么?另外,尽管"scores"每一次都不同,但其大致取值却都差不多,这又是为什么?
尽管"scores"每一次都不同,但其大致取值却都差不多是因为:直接使用初始化后的网络对一个批次的图片进行预测,由于网络没有开始学习即未从数据中获取任何信息,所以对于这个“十分类问题”,网络只是在“瞎猜”每张图片属于哪种类别,从数学意义上讲,在没有任何其他信息的情况下,网络判断一张图片为各个类别的期望是0.1,因此,从最终"scores"每一次的输出来看,它的取值均约等于0.1(略大于,由于是将概率1分为10份,且对于计算机实现来说不会恰好全部等于0.1)。
# 现在我们可以将自动求导功能打开,为训练做好准备
print(torch.set_grad_enabled(True))
4. 训练神经网络
在这一部分中,我们将在数据集 MNIST 上训练构建好的神经网络。
在定义完神经网络之后,我们还需要在 torch.nn 包中选择合适的损失函数 (loss function) 来评估网络输出与理想值之间的差别。常用的损失函数都已经定义在了 torch.nn 中,比如均方误差 (nn.MSELoss)、多分类的交叉熵 (nn.CrossEntropyLoss) 及二分类的交叉熵 (nn.BCELoss),等等。由于我们将进行手写字体0到9的识别,本次实验我们将选用交叉熵损失函数。
一个损失函数需要一对输入:模型的实际输出和目标输出。基于此,损失函数将计算一个值 (loss) 来评估实际输出距离目标输出有多远。
loss_func = nn.CrossEntropyLoss()
除了损失函数以外,我们还需要一个能更直观的反映分类准确性的函数,方便我们了解训练的情况。请大家阅读并理解以下 get_num_correct 的代码每一步在做什么。
def get_num_correct(preds, labels): # get the number of correct times
return preds.argmax(dim=1).eq(labels).sum().item()
在深度学习的训练过程中,我们需要通过不断调整参数使得损失最小化。优化算法就是一种调整模型参数更新的策略。在这里,我们需要用到一个新的包:torch.optim,其中“optim”是“optimizer”的缩写,它包含了多种常用的优化算法。
import torch.optim as optim
本次实验我们将使用随机梯度下降法 (SGD) 来对网络进行优化。
现在我们已经做好了训练的前期准备。在开始大规模的训练前,我们先来观察一个批次 (batch) 的图片是如何被训练的。
首先,我们取出一个 batch 的样本,传递给 network,并计算损失。
batch = next(iter(train_loader))
images, labels = batch
preds = network(images)
loss = loss_func(preds, labels)
print(loss.item())
2.31160044670105
现在我们有了 loss,下一步可以计算偏导 (gradients)。为了计算偏导,我们会在损失张量上调用反向函数 loss.backward(),PyTorch 会自动帮我们做相关的计算。
loss.backward()
我们可以看看100张图片中分类正确的次数:
print(get_num_correct(preds, labels))
11
下一步是使用这些偏导来更新网络的权重。
我们将同一批样本再次传递给更新后的神经网络,看看 loss 和分类正确的次数有什么变化。
preds = network(images)
loss = loss_func(preds, labels)
print("loss: ", loss.item())
print("number of correct times: ", get_num_correct(preds, labels))
loss: 2.3089065551757812
number of correct times: 11
可以看到 loss 有些微的下降,说明我们确实是在朝着损失减小的方向调整参数。下面我们来完整实现整个训练过程。
total_epochs = 10
for epoch in range(total_epochs): # 训练周期
total_loss = 0
total_train_correct = 0
for batch in train_loader: # get a batch from the dataloader
# 读取样本数据,完成正向传播,计算损失
##################### please finish the code ########################
# images, labels = XXX
# preds = XXX
# loss = XXX
images, labels = batch
preds = network(images)
loss = loss_func(preds, labels)
################################ end ################################
# 下面这行非常重要,它使得优化器 (optimizer) 将权重的偏导重新归零;
# 如果不归零,那么在反向传播时,计算出来的偏导会累加在原先的偏导上,
# 造成错误。
optimizer.zero_grad()
# 完成反向传播,更新参数
##################### please finish the code ########################
# 反向传播 (一行代码)
loss.backward()
# 更新参数 (一行代码)
optimizer.step()
################################ end ################################
total_loss += loss.item()
total_train_correct += get_num_correct(preds, labels)
print("epoch:", epoch,
"correct times:", total_train_correct,
f"training accuracy:", "%.3f" %(total_train_correct/len(train_set)*100), "%",
"total_loss:", "%.3f" %total_loss)
epoch: 0 correct times: 53088 training accuracy: 88.480 % total_loss: 214.314
epoch: 1 correct times: 58428 training accuracy: 97.380 % total_loss: 49.868
epoch: 2 correct times: 58906 training accuracy: 98.177 % total_loss: 34.823
epoch: 3 correct times: 59105 training accuracy: 98.508 % total_loss: 28.300
epoch: 4 correct times: 59271 training accuracy: 98.785 % total_loss: 23.302
epoch: 5 correct times: 59371 training accuracy: 98.952 % total_loss: 20.107
epoch: 6 correct times: 59428 training accuracy: 99.047 % total_loss: 17.641
epoch: 7 correct times: 59505 training accuracy: 99.175 % total_loss: 15.261
epoch: 8 correct times: 59578 training accuracy: 99.297 % total_loss: 13.247
epoch: 9 correct times: 59599 training accuracy: 99.332 % total_loss: 11.920
训练结果看上去不错,让我们在测试集上看看准确率如何。
total_test_correct = 0
total_loss = 0
for batch in test_loader: # get a batch from the dataloader
images, labels = batch
preds = network(images)
loss = loss_func(preds, labels)
total_loss += loss
total_test_correct += get_num_correct(preds, labels)
print("correct times:", total_test_correct,
f"test accuracy:", "%.3f" %(total_test_correct/len(test_set)*100), "%",
"total_loss:", "%.3f" %total_loss)
correct times: 9899 test accuracy: 98.990 % total_loss: 3.296