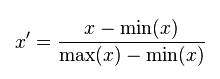机器学习__02__机器学习工程实践

1.0模型评估指标

1.1回归模型评估指标

  回归模型任务目标是，使得预测值能尽量拟合实际值。

常用性能度量方式：

• 绝对误差
• 均方误差

1.1.1绝对误差

  绝对误差即预测点与真实点之间的距离之差的绝对值

1.1.2均方误差

  均方误差即预测点与实际点之间距离之差的平方和均值

1.2分类模型评估指标

​   分类模型的评估指标很多，不同评估指标的侧重点可能不同，有时不同的评估指标彼此之间甚至有可能相互冲突，精度和召回率就是一对矛盾量。

1.2.1 准确率

  准确率是用来衡量模型对数据集中的样本预测正确的比例。

  准确率=预测正确样本数/参与预测的样本总数

from sklearn.metrics import accuracy_score #引入sklearn计算库

y_true=[1,2,3,4,5,6,7,8,9,10]
y_pred=[1,2,3,4,5,6,2,2,2,2]

Accuracy=accuracy_score(y_true,y_pred,normalize=True)

1.2.2 精度

知识点补充：

TP：true positive，被判定为正样本，事实上也是正样本；

TN：true negative，被判定为负样本，事实上也是负样本；

FP：false positive，被判定为正样本，但事实上是负样本；

FN：false negative，被判定为负样本，但事实上是正样本

  精度指的是所有预测为正例的样本，（TP+FP）中真正为正例的样本（TP）的比率，一般来说，就是你找到的信息中真正是我想要的有多少，又叫查准率。

1.2.3 召回率

  表示在所有实际正向数据中，有多少预测正确了，与灵敏度一样。

​ Rec=TP/(TP+FN)

​ 用来评价你有没有把样本中所有的真的正例全部找出来，所以又称为查准率

1.2.4 F1值

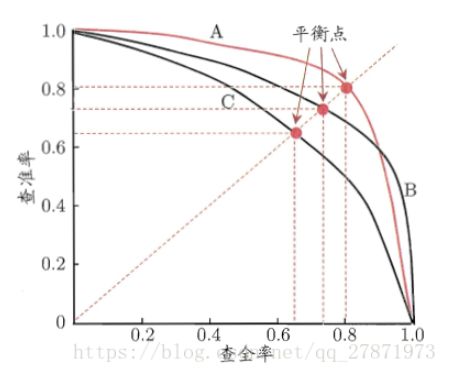
​   查准率和查全率是一对矛盾的指标，一般说，当查准率高的时候，查全率一般很低；查全率高时，查准率一般很低。

​   比如：若我们希望选出的西瓜中好瓜尽可能多，即查准率高，则只挑选最优把握的西瓜，算法挑选出来的西瓜（TP+FP）会减少，相对挑选出的西瓜确实是好瓜（TP）也相应减少，但是分母（TP+FP）减少的更快，所以查准率变大；在查全率公式中，分母（所有好瓜的总数）是不会变的，分子（TP）在减小，所以查全率变小。
​   在实际的模型评估中，单用Precision或者Recall来评价模型是不完整的，评价模型时必须用Precision/Recall两个值。这里介绍三种使用方法：平衡点（Break-Even Point，BEP）、F1度量、F1度量的一般化形式。

​

1.2.5 ROC曲线

​   ROC曲线起源于第二次世界大战时期雷达兵对雷达的信号判断。当时每一个雷达兵的任务就是去解析雷达的信号，但是当时的雷达技术还没有那么先进，存在很多噪声（比如一只大鸟飞过），所以每当有信号出现在雷达屏幕上，雷达兵就需要对其进行破译。有的雷达兵比较谨慎，凡是有信号过来，他都会倾向于解析成是敌军轰炸机，有的雷达兵又比较神经大条，会倾向于解析成是飞鸟。这个时候，雷达兵的上司就很头大了，他急需一套评估指标来帮助他汇总每一个雷达兵的预测信息，以及来评估这台雷达的可靠性（如果不论哪一类雷达兵都能准确预测，那这台雷达就很NB～读者可思考其缘由）。于是，最早的ROC曲线分析方法就诞生了，用来作为评估雷达可靠性的指标～在那之后，ROC曲线就被广泛运用于医学以及机器学习领域

​ ROC曲线就是将真正率作为纵轴，假正率作为横轴所绘制的图形。

​   举一个简单的例子方便大家的理解，还是刚才雷达的例子。假设现在有10个雷达信号警报，其中8个是真的轰炸机（P）来了，2个是大鸟（N）飞过，经过某分析员解析雷达的信号，判断出9个信号是轰炸机，剩下1个是大鸟，其中被判定为轰炸机的信号中，有1个其实是大鸟的信号（FP=1），而剩下8个确实是轰炸机信号（TP=8）。因此可以计算出FPR为，TPR为，而就对应ROC曲线上一点（0.5,1）

​   从这里我们可以理解：我们所期望的是，TP越大越好，FP越小越好。

如果一条曲线包裹另一条曲线，则外面曲线的性能更优

1.2.6 AUC

​   当两条ROC曲线发生交叉时，谁的性能更优就难以判定了，这时就要根据两条ROC曲线下面的面积大小来比较判断，即面积大者相对更优，这个ROC曲线下面的面积就是AUC。

1.2.7混淆矩阵

​   时一种评估分类模型好坏的形象化展示工具。例如有150个样本数据，把这些数据平均分成三类，每类50个分类结束后得到的混淆矩阵如下：

​   每行之和为50个，表示50个样本，第一行说明类1的50个样本中有43个分类正确，5个错分类为2,2个错分为类3。

​   由此可以看出，如果混淆矩阵中非对角线元素为0，则表示一个完美的分类器。

1.3聚类模型评估指标

​   聚类是将样本集划分为若干个不相交的子集，即样本簇，同时需要通过某些性能度量方式来评估其聚类结果的好坏。用机器学习的语言来讲，希望簇内相似度高，簇建相似度低。

1.3.1外部指标

  外部指标需要提供一个参考模型，然后将聚类结果与该参考模型进行比较得到一个评判值；

常用系数

• Jaccard系数
• FM指数
• Rand指数
• 标准化互信息

1.3.2内部指标

内部指标不需要有外部参考模型，可直接通过考察聚类结果得到

常用指数：

• DB指数
• Dunn指数

1.3.3轮廓系数

​   轮廓系数适用于训练样本类别未知的情况。假设某个样本点与它同类别的群内点的平均距离为a，与他距离最近的非同类别的群外点的平均距离为b则轮廓系数定义为。
$$s=b-a/max(a,b)$$
​   对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。

​   轮廓系数的取值范围是[-1,1],同类别样本点的距离越近，且不同类别的样本点距离越远，则得到的轮廓系数的值就越大。

1.4常用距离公式

1.曼哈顿距离

2.欧式距离

3.闵可夫斯基距离

4.切比雪夫距离

5.汉明距离

6.杰卡德相似系数

7.杰卡德距离

2.0模型复杂度量度

2.1偏方与方差

​   偏差:是衡量预测值与真实值的关系,是指预测值与真实值之间的差值.

​   方差:是衡量预测值之间的关系,和真实值无关.也就是他们的离散程度

​   误差 = 偏差 + 方差

2.2过拟合与正则化

2.2.1过拟合与欠拟合

​   第一个模型是一个线性模型，处于欠拟合状态，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。

2.2.2经验风险与结构风险

​   训练数据集的平均损失称为经验风险。度量平均意义下模型预测效果的好坏

​   结构风险是在经验风险的基础上加上表示模型复杂度的正则项（罚项）

2.2.3正则化

  机器学习中经常会在损失函数中加入正则项，称之为正则化（Regularize）。

  目的：防止模型过拟合

  原理：在损失函数上加上某些规则（限制），缩小解空间，从而减少求出过拟合解的可能性

3.0特征工程与模型调优

​   完成常用科学计算库的学习，以及模型的评估指标与复杂度度量，下面的内容介绍机器学习项目中的特征工程，模型选择与模型调优。

3.1数据挖掘项目流程

（1）业务理解

（2）数据分析

（3）特征工程

（4）模型选择

（5）模型评估

（6）项目落地

3.2特征工程

3.2.1数据清洗

（1）直接删除缺失数据

（2）固定值填充

（3）均值中位数填充

（4）相邻值填充

（5）模型预测填充

3.2.2特征处理

1.归一化和标准化

​   数据标准化（Normalization），也称为归一化，归一化就是将你需要处理的数据在通过某种算法经过处理后，限制将其限定在你需要的一定的范围内。

（1）线性归一化，也称min-max标准化、离差标准化；是对原始数据的线性变换，使得结果值映射到[0,1]之间。转换函数如下：

  这种归一化比较适用在数值较集中的情况。但是这种方法有一个缺陷，就是如果max和min不稳定的时候，很容易使得归一化的结果不稳定，易受极值影响，影响后续使用效果。所以在实际应用中，我们一般用经验常量来替代max和min。

（2）标准差归一化，也叫Z-score标准化，这种方法给予原始数据的均值（mean，μ）和标准差（standard deviation，σ）进行数据的标准化。经过处理后的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

（3）非线性归一化，这种方法一般使用在数据分析比较大的场景，有些数值很大，有些很小，通过一些数学函数，将原始值进行映射。一般使用的函数包括log、指数、正切等，需要根据数据分布的具体情况来决定非线性函数的曲线。

2.离散化

​   就是把无限空间中有限的个体映射到有限的空间中。数据离散化操作大多是针对连续数据进行的，处理之后的数据值域分布将从连续属性变为离散属性。

​   为什么离散化：模型中，同一线性系数应该对所有可能的计数值起作用。过大的计数值对无监督学习方法也会造成破坏，比如k-均值聚类，它使用欧氏距离作为相似度函数来测量数据点之间的相似度。数据向量某个元素中过大的计数值对相似度的影响会远超其他元素，从而破坏整体的相似度测量。

• 离散化方式会影响后续数据建模和应用效果：
• 使用决策树往往倾向于少量的离散化区间，过多的离散化将使得规则过多受到碎片区间的影响。
• 关联规则需要对所有特征一起离散化，关联规则关注的是所有特征的关联关系，如果对每个列单独离散化将失去整体规则性。

3.2.3特征交互

​   特征交互就是人为的或者通过构造模型，自动将两个或两个两个以上的特征进行交互常用的交互方式有，求和、相乘、取对数等。

3.2.4特征映射

​   特征映射是一个比特征交互更高级的问题，一般通过某些机器学习模型来实现。

3.3模型选择与模型调优

3.3.1模型选择

（1）数据集切分

​   使用cross_validation类中的train_test_split函数可以很容易地将原始数据按照比例切成训练集和验证集。

（2）交叉验证

​   也是一种模型验证技术。简单来说就是重复使用数据。除去测试集，把剩余数据进行划分，组合成多组不同的训练集和验证集，某次在训练集中出现的样本下次可能成为验证集中的样本，这就是所谓的“交叉”。最后用各次验证误差的平均值作为模型最终的验证误差。

​   如果验证集较大，那么训练集就会变得很小，如果数据集本身就不大的话，显然这样训练出来的模型就不好。如果验证集很小，那么此验证误差就不能很好地反映出泛化误差。此外，在不同的划分方式下，训练出的不同模型的验证误差波动也很大（方差大）。到底以哪次验证误差为准？谁都不知道。但是如果将这些不同划分方式下训练出来的模型的验证过程重复多次，得到的平均误差可能就是对泛化误差的一个很好的近似。

3.3.2模型调优

在模型选定后，一般还需要进行模型的参数调优，这里我们介绍，网格搜索寻优和随机搜索寻优

（1）网格搜索寻优

​   网格搜索寻优是一种暴力寻优方法，做法是将某些参数放在网格中，通过遍历的方式，用交叉验证对参数空间进行求解，寻找最佳的参数。

（2）随机搜索寻优

​   在参数较少的时候，采用暴力寻优是可以的，但是当参数过多的时候，或者当参数为连续值时候，暴力寻优明显不大可取，所以提出随机搜索寻优的方式，其做法是对这些连续值进行采样，从中挑选出一些值作为代表。